- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Вычисление тройных интегралов. Цилиндрические координаты. (Семинар 32) презентация
Содержание
- 1. Вычисление тройных интегралов. Цилиндрические координаты. (Семинар 32)
- 2. Вычисление тройных интегралов. Цилиндрические координаты Отнесем
- 3. Связь между декартовыми и цилиндрическими координатами точки
- 4. Сферические координаты Отнесем область интегрирования Т к
- 5. Установим связь между декартовыми и сферическими координатами.
- 6. Примеры с решениями: Вычислить , если
- 7. Вычислить , если область T
- 8. Вычислить , если T – верхняя
- 9. Примеры для самостоятельного решения: Вычислить
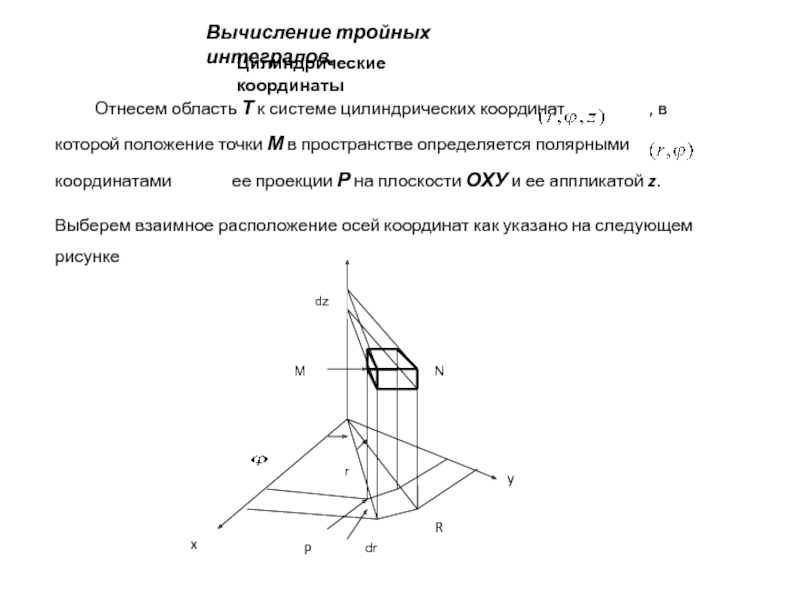
Слайд 2Вычисление тройных интегралов.
Цилиндрические координаты
Отнесем область Т к системе цилиндрических координат
Выберем взаимное расположение осей координат как указано на следующем рисунке
y
R
P
x
Слайд 3Связь между декартовыми и цилиндрическими координатами точки следующая:
(*)
Преобразование интеграла
Для этого нужно в f(x, y, z) переменные x, y, z заменить по формулам (*).
Элемент объема положить равным и вычислить интеграл по области, построенной во вспомогательной системе координат .
Получаем:
Если рассмотреть в качестве области интегрирования внутреннюю часть прямого цилиндра , то все пределы интегрирования постоянны
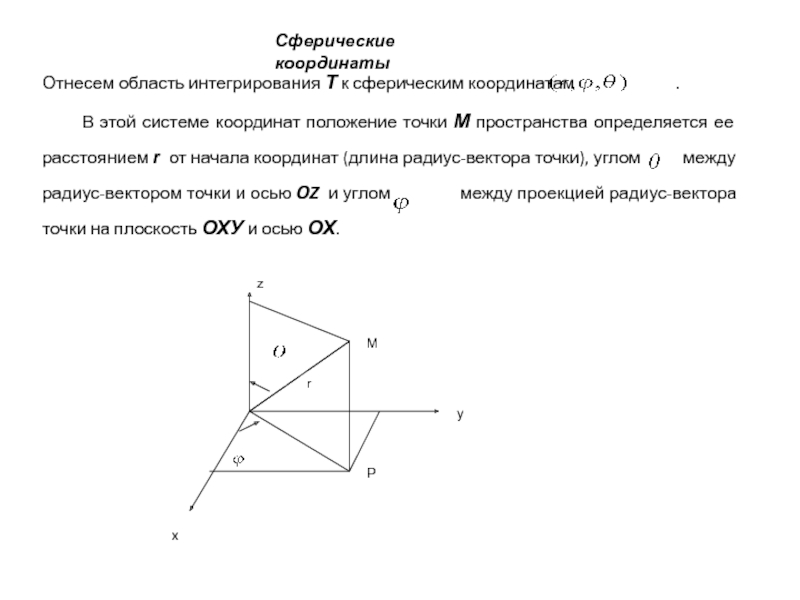
Слайд 4Сферические координаты
Отнесем область интегрирования Т к сферическим координатам
В этой системе координат положение точки М пространства определяется ее расстоянием r от начала координат (длина радиус-вектора точки), углом между радиус-вектором точки и осью OZ и углом между проекцией радиус-вектора точки на плоскость ОХУ и осью ОХ.
x
Слайд 5Установим связь между декартовыми и сферическими координатами.
Из рисунка имеем:
Окончательно:
Для элемента
(**)
Заменив в тройном интеграле x, y, z по формулам (*) и взяв элемент объема равным (**), получаем
Слайд 6Примеры с решениями:
Вычислить
, если T – шар
Решение.
Перейдем к сферическим
В области T координаты
изменяются так:
Следовательно,
Слайд 7Вычислить
, если область T ограничена цилиндром
и плоскостями y=0, z=0,
Решение.
Перейдем к цилиндрическим координатам.
Уравнение цилиндра в этих координатах примет вид:
В области T координаты изменяются так:
Следовательно,
Слайд 8Вычислить
, если T – верхняя половина шара
Решение.
Перейдем к сферическим
В области T координаты
изменяются так:
Следовательно,
Слайд 9Примеры для самостоятельного решения:
Вычислить
, если область T ограничена сферой
и
Вычислить
, если область T ограничена цилиндром
и плоскостями y=0, y=1.
Вычислить
, если T – шар
Вычислить
, если T – шар
Вычислить
, где область T ограничена поверхностями