- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Выпуклый анализ. Минимум выпуклой функции. Лекция 16 презентация
Содержание
- 1. Выпуклый анализ. Минимум выпуклой функции. Лекция 16
- 2. 5. МИНИМУМ ВЫПУКЛОЙ ФУНКЦИИ
- 3. 5.1. Локальный и глобальный
- 6. Доказательство.
- 7. а
- 8. 5.3. Минимум выпуклой функции,
- 9. Доказательство. Необходимость.
- 10. Полагаем
- 11. имеем
- 12. Тогда является обобщением теоремы
- 13. Решение. Таким образом, В этих точках функция является дифференцируемой, поэтому
- 14. Тогда одна из производных должна быть строго отрицательной.
Слайд 2
5. МИНИМУМ ВЫПУКЛОЙ ФУНКЦИИ
5.1. Локальный и глобальный минимум выпуклой функции.
5.2. Минимум дифференцируемой выпуклой функции.
5.3. Минимум выпуклой функции, дифференцируемой
по всем возможным направлениям.
Слайд 3
5.1. Локальный и глобальный минимум выпуклой функции.
Теорема 1.
выпукла.
одновременно является
выпукло.
Доказательство.
Слайд 4
С другой стороны,
или
Таким образом, всякий локальный минимум одновременно является
Тогда
Таким образом,
Слайд 7
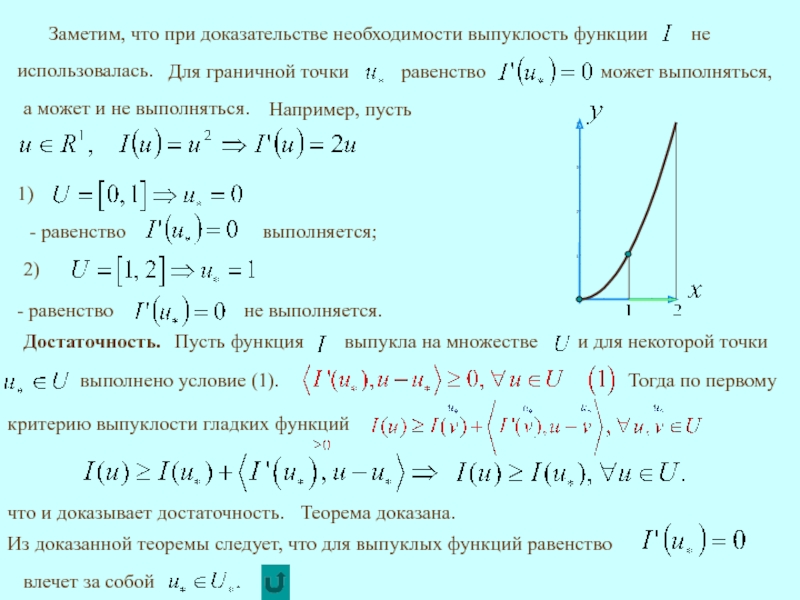
а может и не выполняться.
Например, пусть
Достаточность.
что и доказывает
Теорема доказана.
Слайд 8
5.3. Минимум выпуклой функции, дифференцируемой по всем возможным
направлениям.
Требование существования производных
Это тем более естественно, поскольку всякая выпуклая функция
Теорема 3.
имеет производные по всем возможным направлениям.
имеет производные по всем направлениям.
Слайд 12
Тогда
является обобщением теоремы 2
Таким образом, теорема 3
Получили формулировку теоремы 2.
(функций дифференцируемых
Упражнение.