- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Вычисление объемов тел вращения. Применение интеграла презентация
Содержание
- 1. Вычисление объемов тел вращения. Применение интеграла
- 2. У х y=f(x) O Пусть функция y
- 3. У х y=f(x) O Разобьем отрезок [a;b]
- 6. Тогда объем тела вращения вокруг оси ОХ:
- 7. Задача. Пусть тело образовано вращением параболы
- 8. Задача. Пусть тело образовано вращением функции
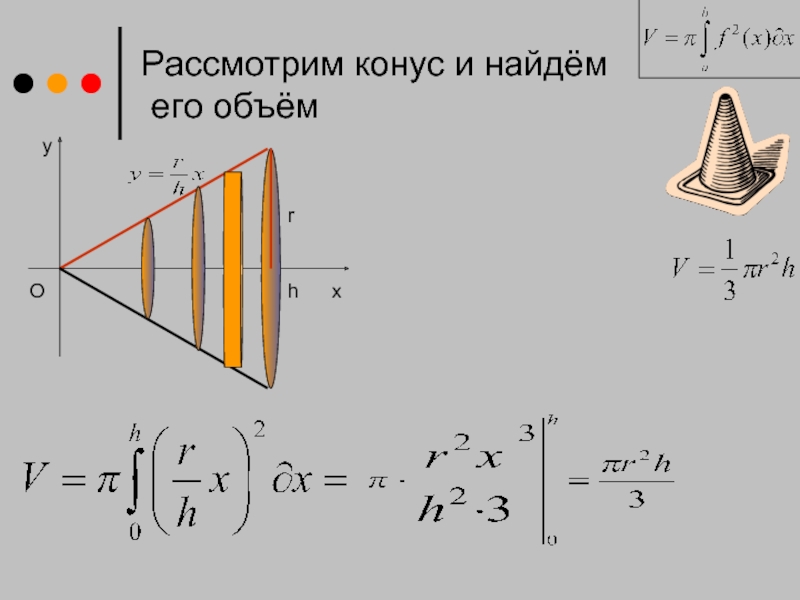
- 9. x Рассмотрим конус и найдём
- 10. x Рассмотрим усечённый конус и найдём
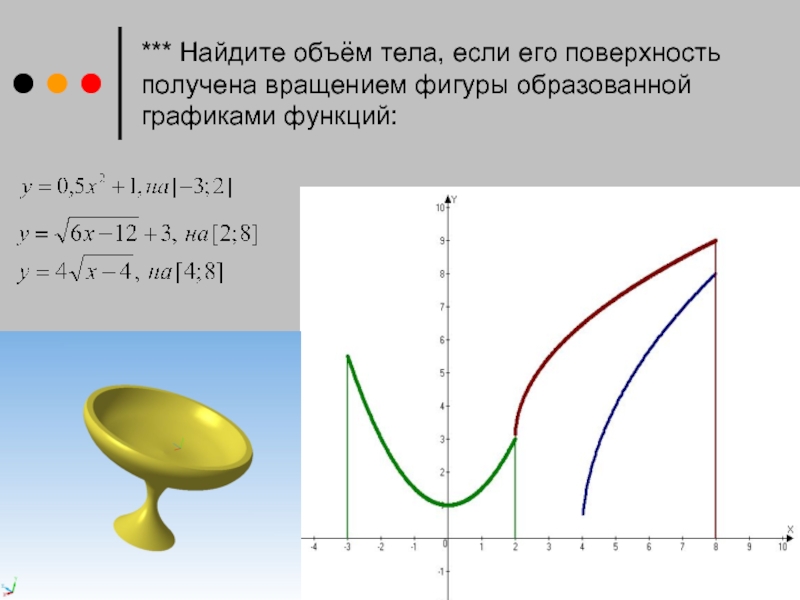
- 11. *** Найдите объём тела, если его поверхность получена вращением фигуры образованной графиками функций:
- 12. Вычисление определённых интегралов
Слайд 2У
х
y=f(x)
O
Пусть функция y = f(x) определена, неотрицательна и непрерывна на отрезке
Рассмотрим тело, образованное вращением этой криволинейной трапеции вокруг оси OX и найдем его объем.
a
b
Постановка задачи
Слайд 3У
х
y=f(x)
O
Разобьем отрезок [a;b] на n частей произвольным образом, через каждую точку
Очевидно, что любое поперечное сечение тела вращения – круг. Радиус круга равен значению функции в хс
Площадь этого круга – S(x) = π· f 2 (xс)
Слайд 4
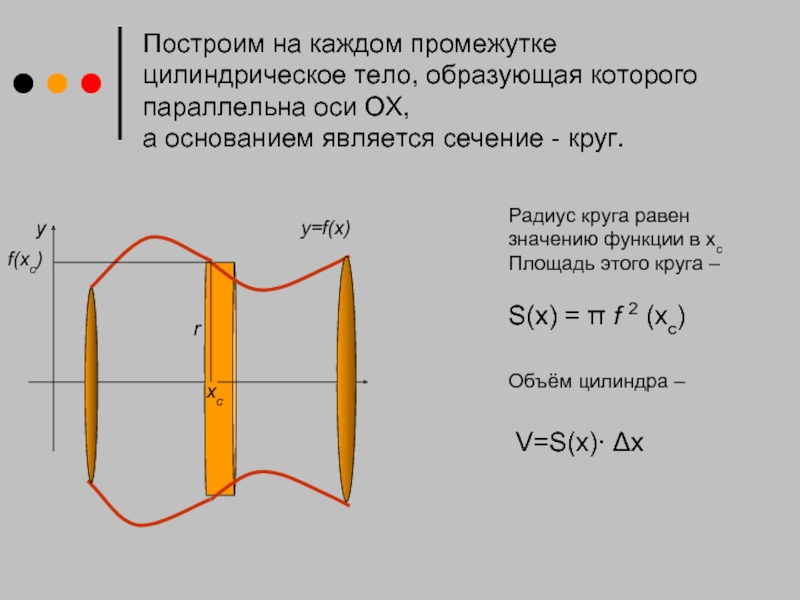
Построим на каждом промежутке цилиндрическое тело, образующая которого параллельна оси ОХ,
а
Радиус круга равен
значению функции в хс
Площадь этого круга –
S(x) = π f 2 (xс)
Объём цилиндра –
V=S(x)∙ Δx
y=f(x)
f(xс)
y
xс
r
Слайд 5
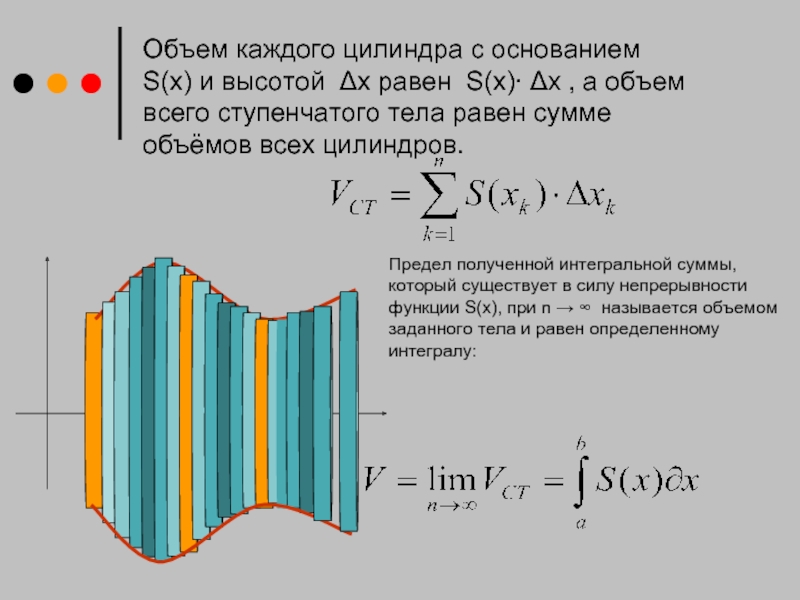
Объем каждого цилиндра с основанием S(x) и высотой Δx равен S(x)∙
Предел полученной интегральной суммы, который существует в силу непрерывности функции S(x), при n → ∞ называется объемом заданного тела и равен определенному интегралу:
Слайд 6Тогда объем тела вращения вокруг оси ОХ:
Если тело образовано вращением криволинейной
Предел полученной интегральной суммы, при n → ∞ равен определенному интегралу:
x
y=f(x)
y
Слайд 7Задача.
Пусть тело образовано вращением параболы у=х2 на отрезке [0;2] вокруг
Найдите объём тела вращения.
у=х2
у
О
х
2
Слайд 8Задача.
Пусть тело образовано вращением функции у=0,5x на отрезке [0;4] вокруг
Найдите объём тела вращения.
y
O
x
4

![Ухy=f(x)OПусть функция y = f(x) определена, неотрицательна и непрерывна на отрезке [a; b], тогда график](/img/tmb/2/116716/cdc534ee925d4210f376b7a203d93d32-800x.jpg)
![Ухy=f(x)OРазобьем отрезок [a;b] на n частей произвольным образом, через каждую точку деления проведем плоскость, перпендикулярную](/img/tmb/2/116716/7dcabbbc8f575dad806731cc6f49e335-800x.jpg)

![Задача. Пусть тело образовано вращением параболы у=х2 на отрезке [0;2] вокруг оси ОХ.Найдите объём тела вращения.у=х2уОх2](/img/tmb/2/116716/121d52331f69a2297092834b845be4ba-800x.jpg)
![Задача. Пусть тело образовано вращением функции у=0,5x на отрезке [0;4] вокруг оси ОХ.Найдите объём тела вращения.yOx4](/img/tmb/2/116716/2bb57a5eaa7de2691ca773dcf80a0ff9-800x.jpg)