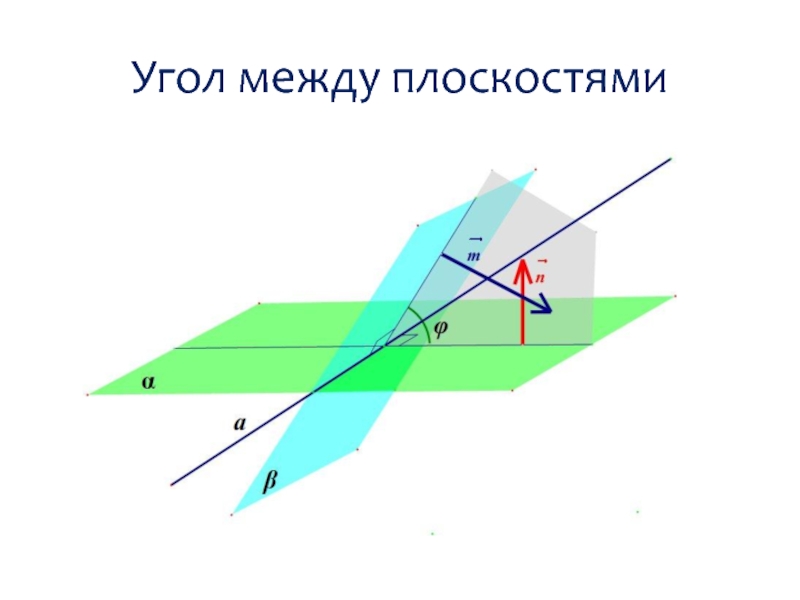
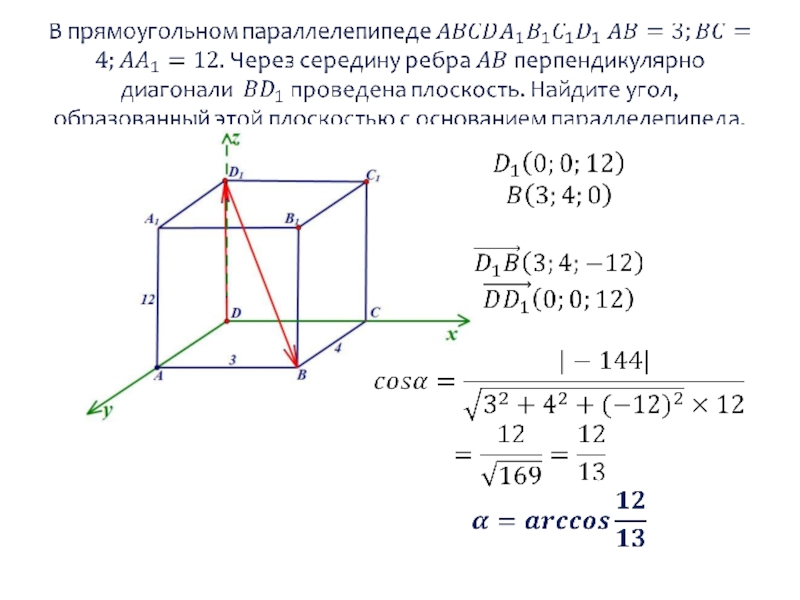
нормали к плоскости
Направляющий вектор прямой
- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Введение в метод координат. Выбор системы координат. Координаты точки. Уравнение плоскости по трем точкам презентация
Содержание
- 1. Введение в метод координат. Выбор системы координат. Координаты точки. Уравнение плоскости по трем точкам
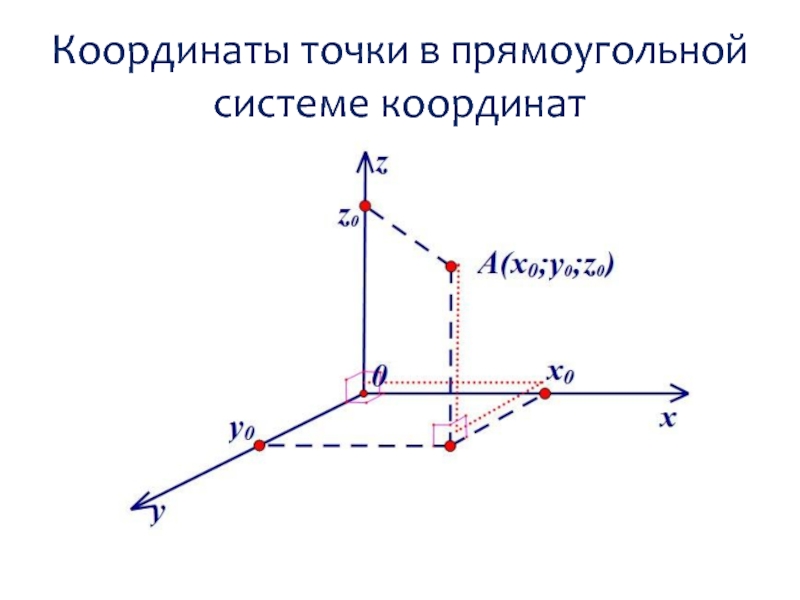
- 2. Координаты точки в прямоугольной системе координат
- 3.
- 4.
- 5.
- 6. Координаты точки Чтобы найти координаты точки нужно:
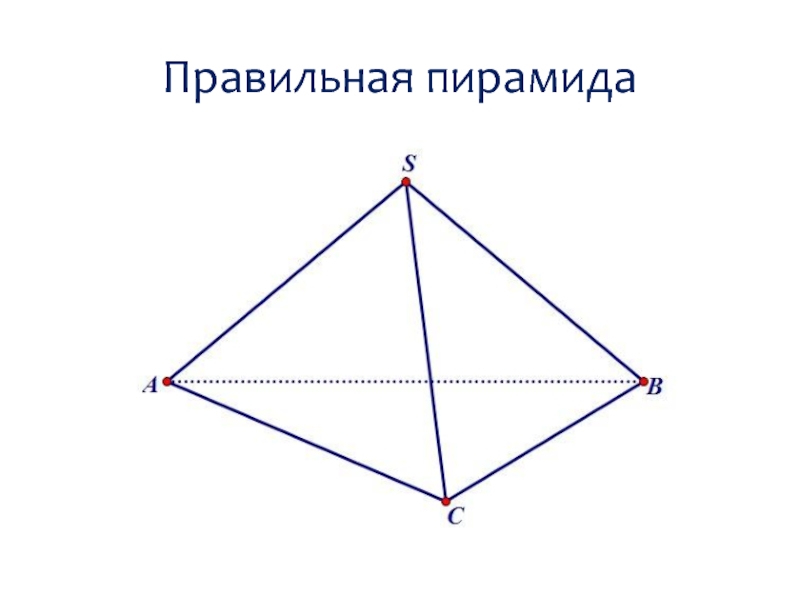
- 7. Правильная пирамида
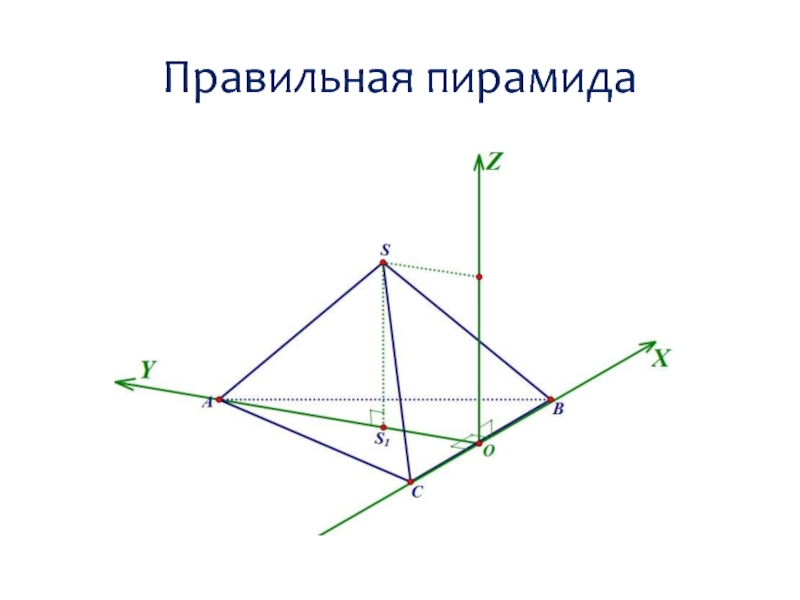
- 8. Правильная пирамида
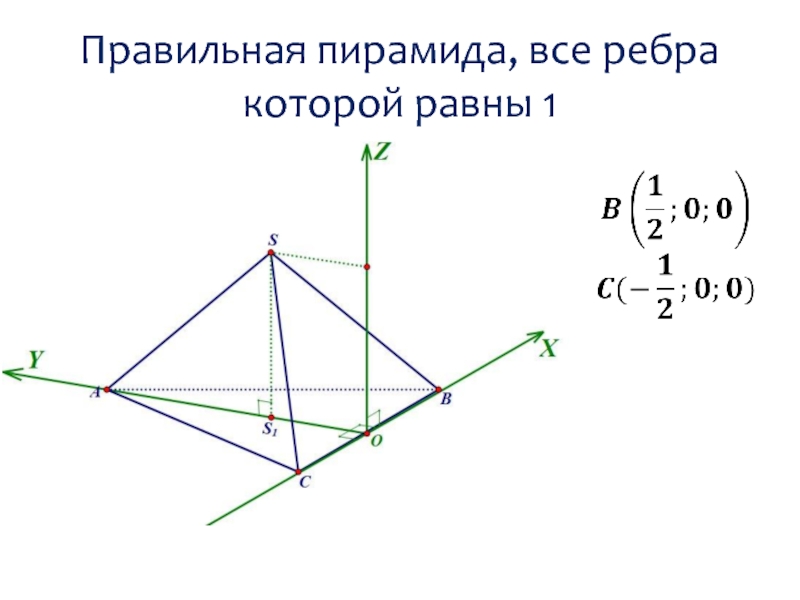
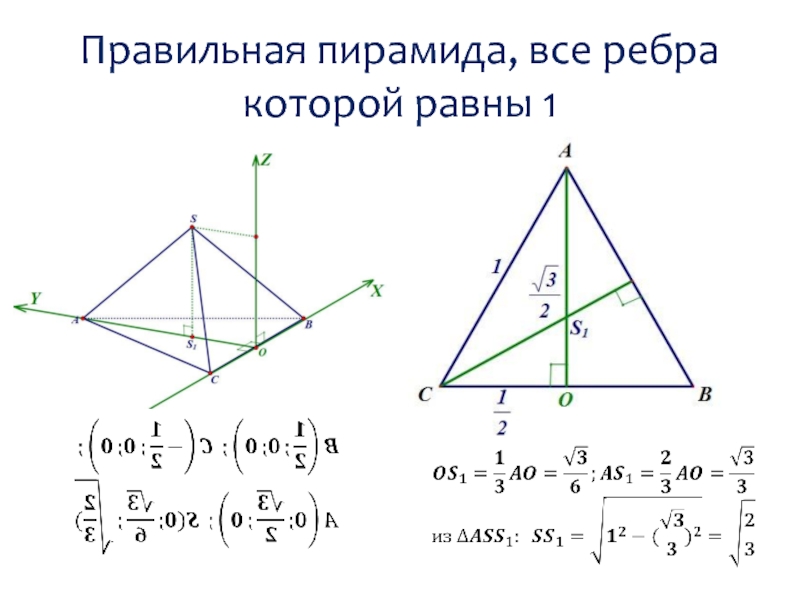
- 9. Правильная пирамида, все ребра которой равны 1
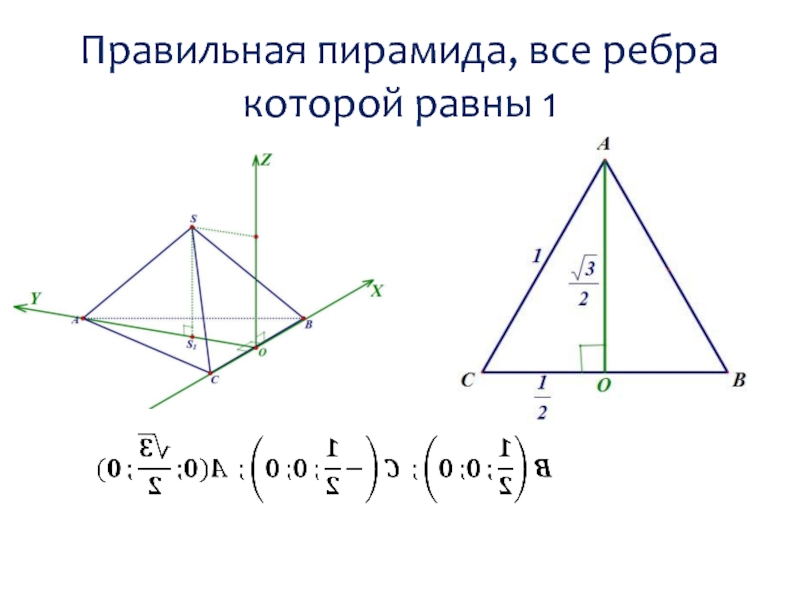
- 10. Правильная пирамида, все ребра которой равны 1
- 11. Правильная пирамида, все ребра которой равны 1
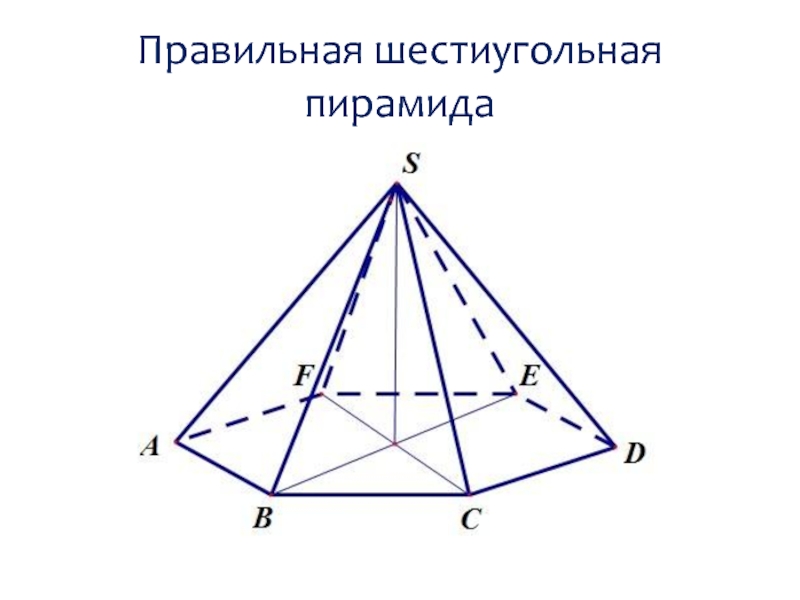
- 12. Правильная шестиугольная пирамида
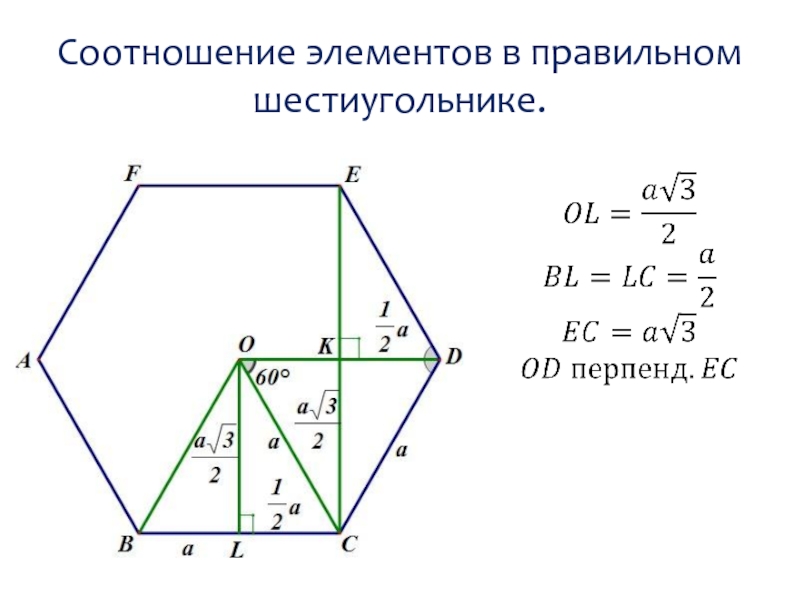
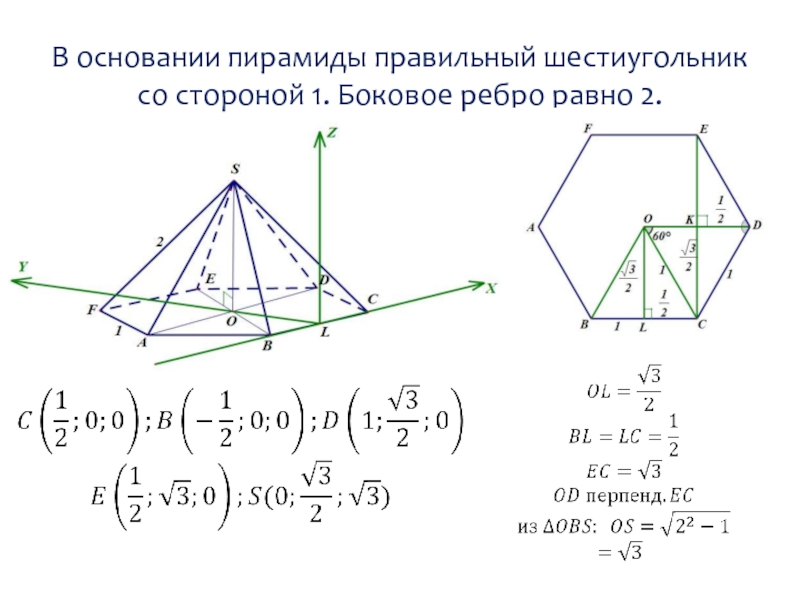
- 13. Соотношение элементов в правильном шестиугольнике.
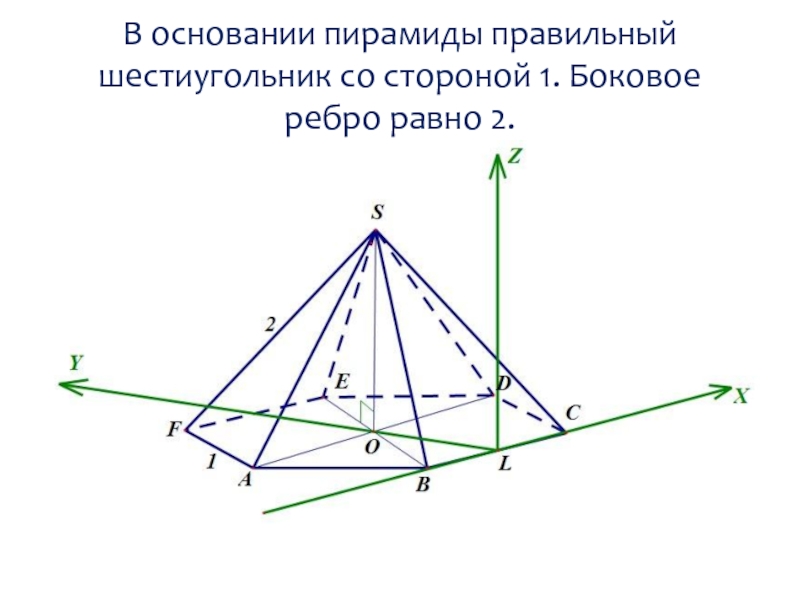
- 14. В основании пирамиды правильный шестиугольник со стороной 1. Боковое ребро равно 2.
- 15. В основании пирамиды правильный шестиугольник со стороной 1. Боковое ребро равно 2.
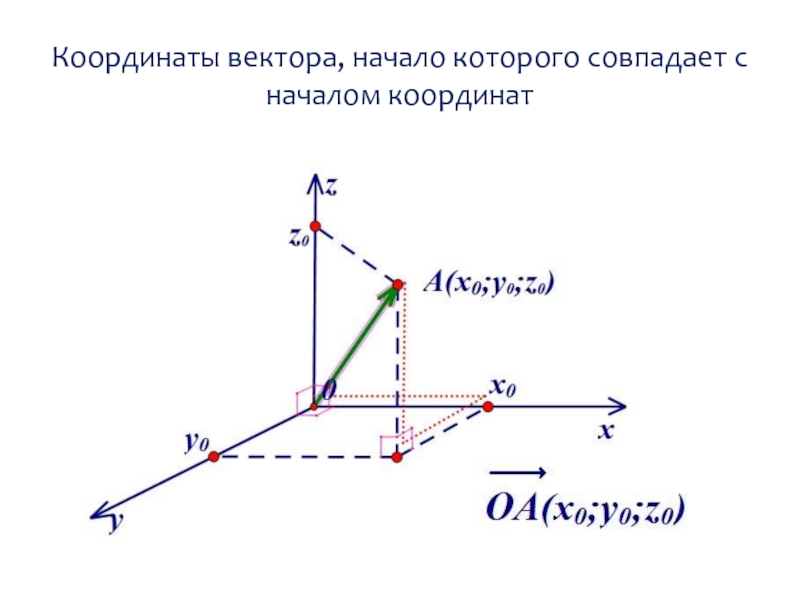
- 16. Координаты вектора, начало которого совпадает с началом координат
- 17. Координаты вектора, заданного координатами его концов
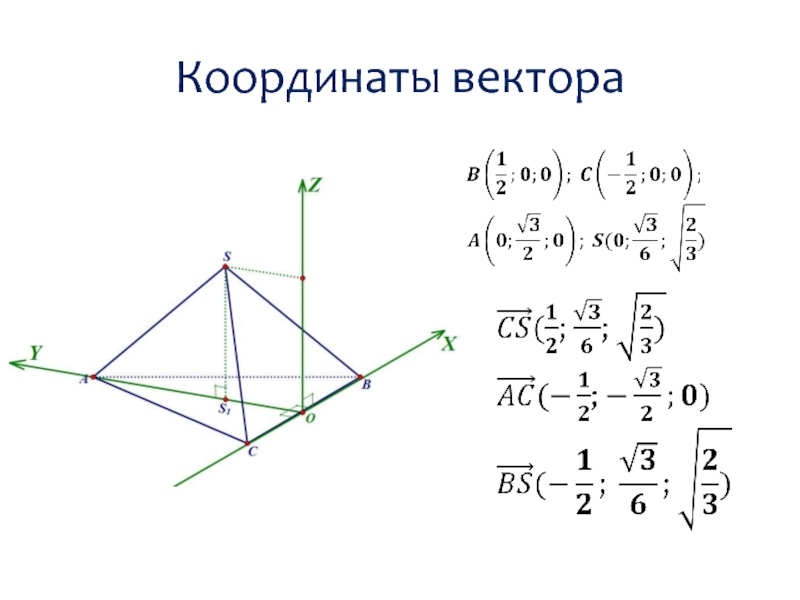
- 18. Координаты вектора
- 19.
- 20.
- 21.
- 22.
- 23.
- 24.
- 25.
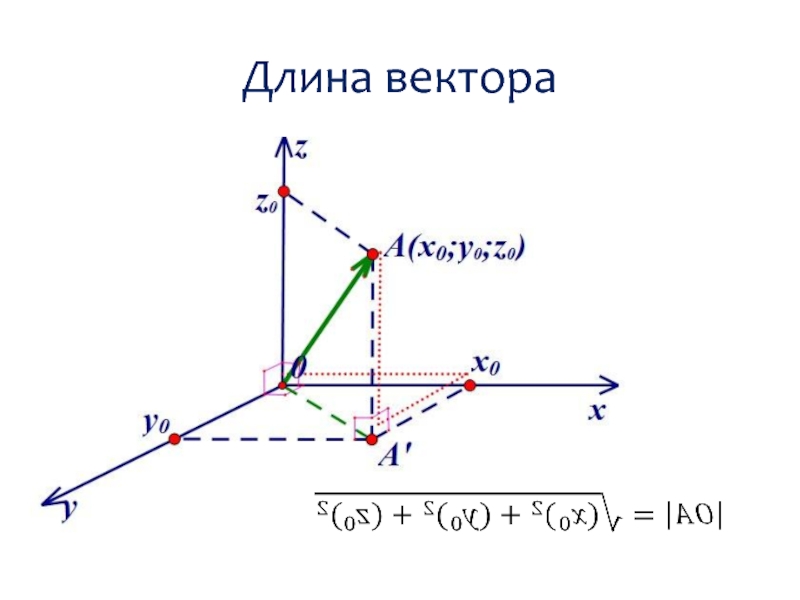
- 26. Длина вектора
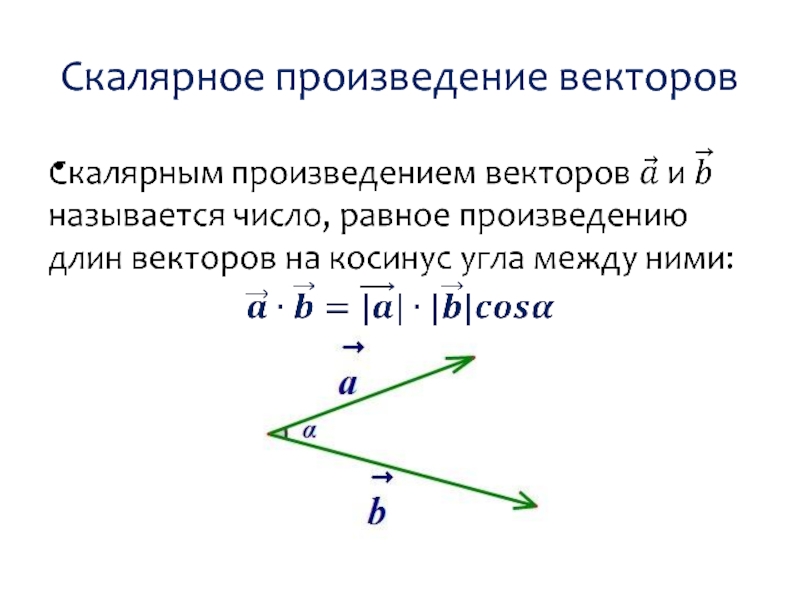
- 27. Скалярное произведение векторов
- 28. Скалярное произведение векторов
- 29. Косинус угла между векторами
- 30. Условие перпендикулярности векторов
- 31. Угол между пересекающимися прямыми Углом
- 32. Угол между пересекающимися прямыми Косинус угла
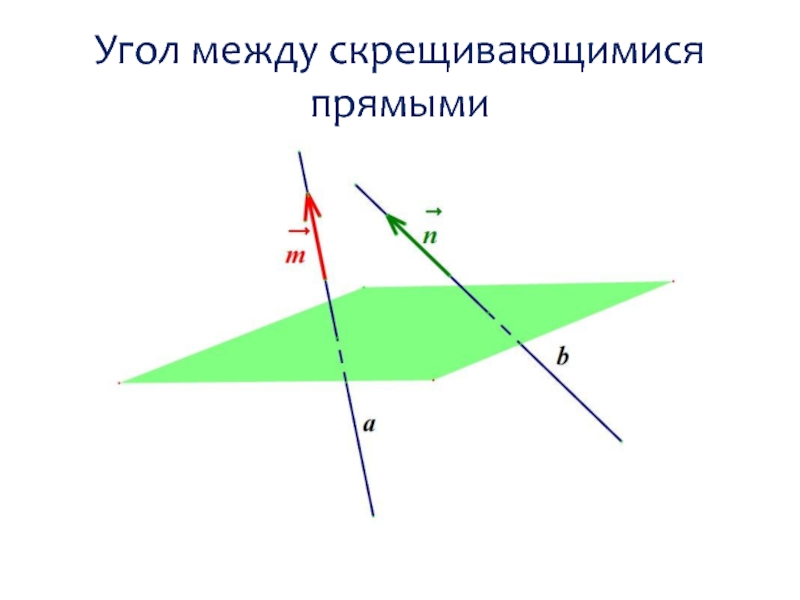
- 33. Угол между скрещивающимися прямыми
- 34. Угол между скрещивающимися прямыми
- 35. В правильной треугольной пирамиде ABCS, все ребра
- 36. В правильной треугольной пирамиде ABCS, все ребра
- 37. В правильной треугольной пирамиде ABCS, все ребра
- 38. Уравнение плоскости
- 39. Уравнение плоскости
- 40. Уравнение плоскости
- 41. Уравнение плоскости
- 42.
- 43.
- 44.
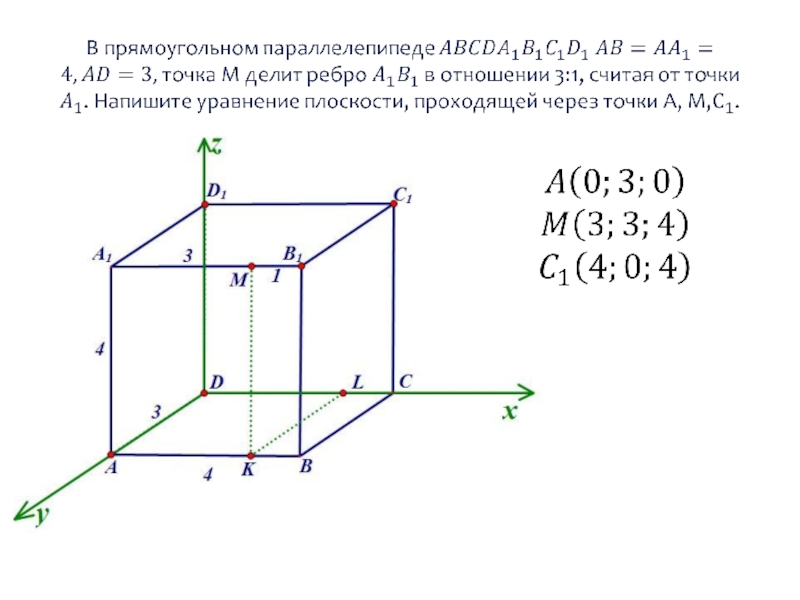
- 45. Уравнение плоскости
- 46.
- 47.
- 48.
- 49.
- 50.
- 51.
- 52.
- 53.
- 54.
- 55. Угол между плоскостями
- 56. Угол между плоскостями Угол между
- 57. Угол между плоскостями
- 58. Угол между плоскостями
- 59.
- 60.
Слайд 1Введение в метод координат
Выбор системы координат
Координаты точки
Уравнение плоскости по трем точкам
Вектор
Слайд 6Координаты точки
Чтобы найти координаты точки нужно:
Найти проекцию этой точки на плоскость
OXY.
Найти координаты проекции в плоскости OXY.
Найти проекцию точки на ось OZ
Записать третью координату.
Найти координаты проекции в плоскости OXY.
Найти проекцию точки на ось OZ
Записать третью координату.
Слайд 31
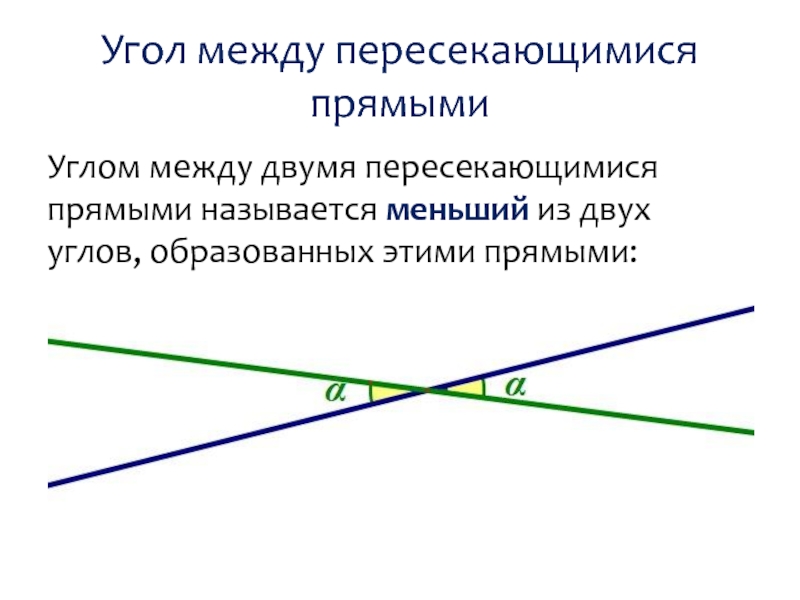
Угол между пересекающимися прямыми
Углом между двумя пересекающимися прямыми называется меньший из
двух углов, образованных этими прямыми:
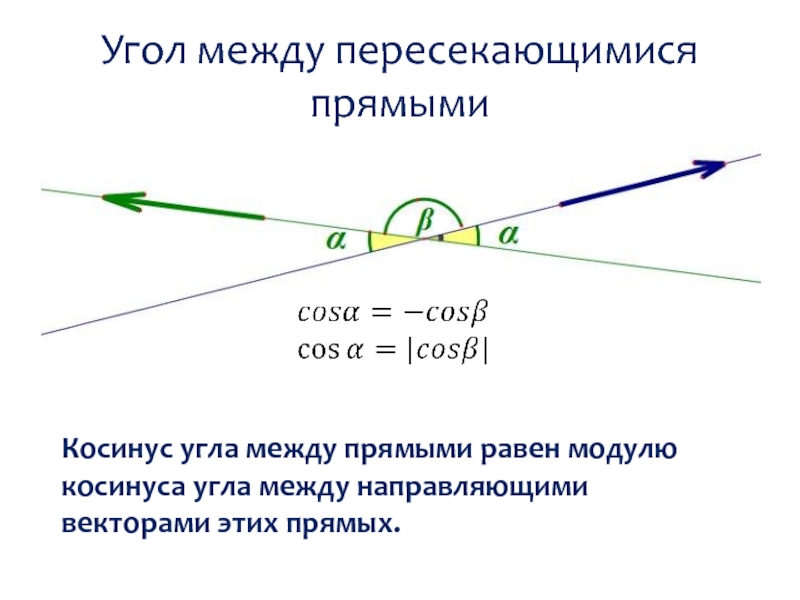
Слайд 32Угол между пересекающимися прямыми
Косинус угла между прямыми равен модулю косинуса угла
между направляющими векторами этих прямых.
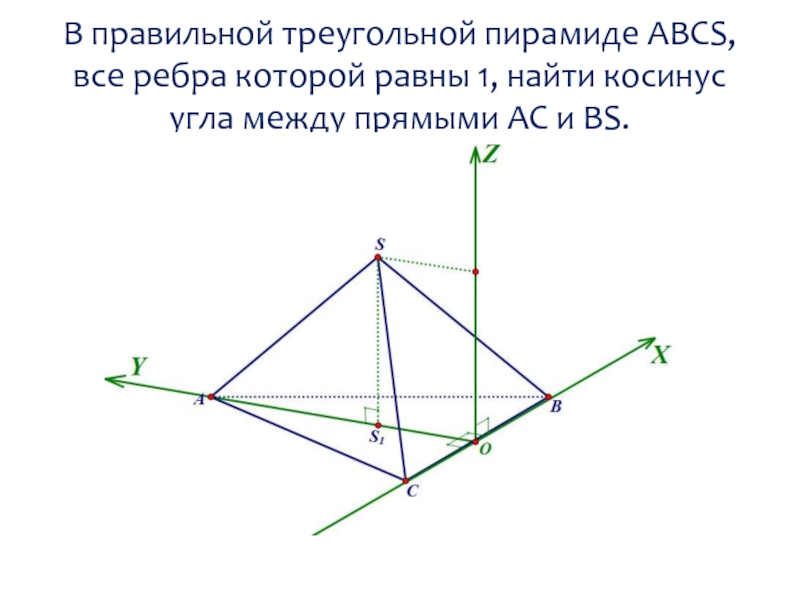
Слайд 35В правильной треугольной пирамиде ABCS, все ребра которой равны 1, найти
косинус угла между прямыми АС и BS.
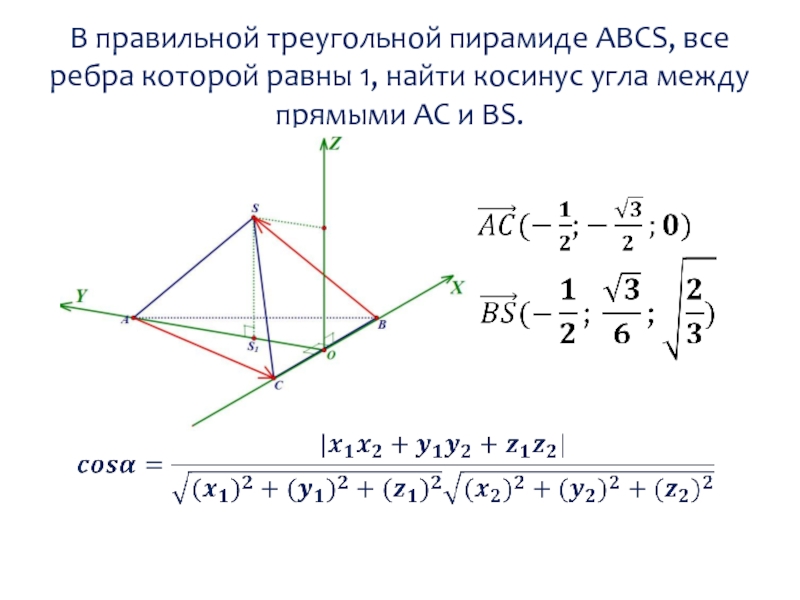
Слайд 36В правильной треугольной пирамиде ABCS, все ребра которой равны 1, найти
косинус угла между прямыми АС и BS.
Слайд 37В правильной треугольной пирамиде ABCS, все ребра которой равны 1, найти
косинус угла между прямыми АС и BS.
Слайд 56
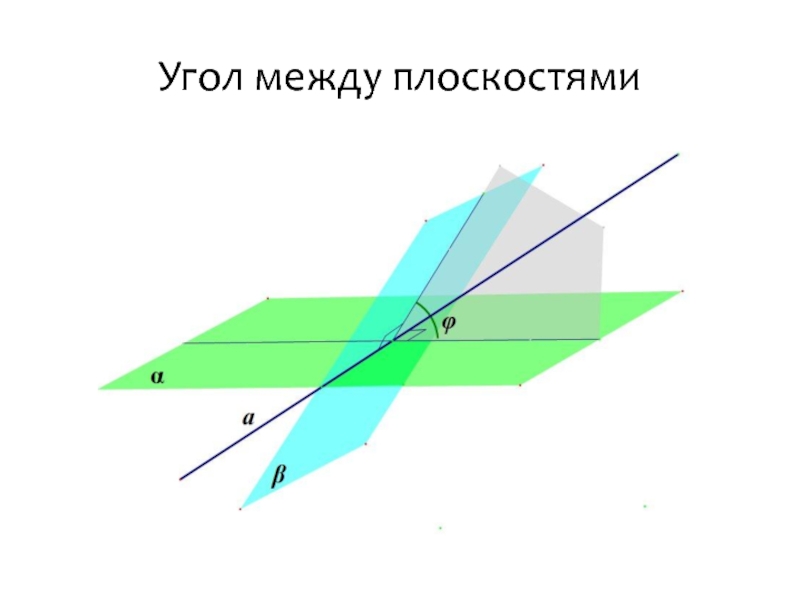
Угол между плоскостями
Угол между двумя плоскостями – это меньший из двух
углов, образованных этими плоскостями.
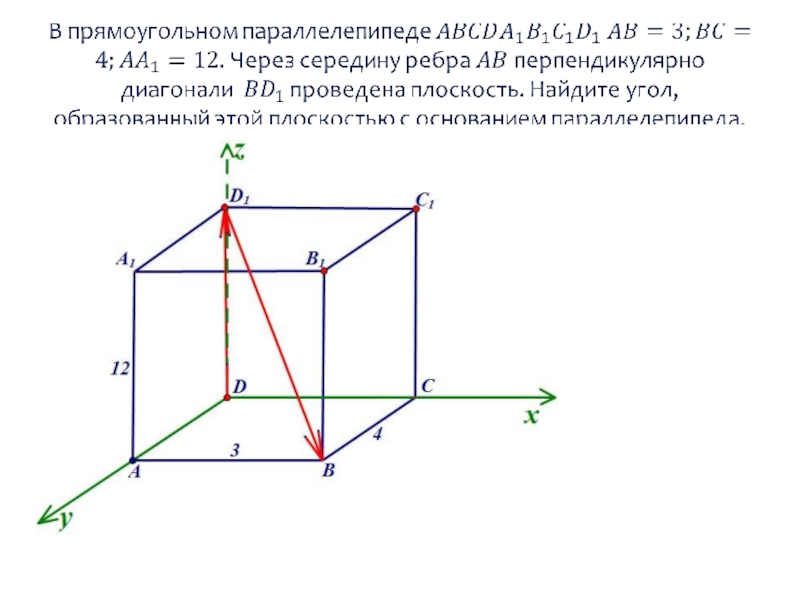
Угол между двумя плоскостями равен меньшему из двух двугранных углов, образованных этими плоскостями. Линейный угол двугранного угла – это угол между двумя перпендикулярами, лежащими в этих плоскостях, проведенными к линии пересечения плоскостей. Двугранный угол измеряется величиной линейного угла.
Угол между двумя плоскостями равен меньшему из двух двугранных углов, образованных этими плоскостями. Линейный угол двугранного угла – это угол между двумя перпендикулярами, лежащими в этих плоскостях, проведенными к линии пересечения плоскостей. Двугранный угол измеряется величиной линейного угла.