- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Логика высказываний. Таблицы истинности презентация
Содержание
- 1. Логика высказываний. Таблицы истинности
- 2. Вопросы на повторение Какие основные логические операции
- 3. Таблицы истинности Решение логических выражений принято оформлять
- 4. Определение Таблица истинности - это таблица, с
- 5. Для составления таблицы истинности необходимо: Количество строк
- 6. Пример 1 Построим таблицу истинности для функции
- 7. Пример 1. Таблица 0 1 1 1
- 8. Пример 2 Построим таблицу истинности для функции
- 9. Пример. Таблица 0 0 0 0 1
- 10. Домашнее задание
Слайд 2Вопросы на повторение
Какие основные логические операции вам известны?
Составьте пример логического выражения
с операциями отрицание, И (ИЛИ):
А=“Сегодня 30 сентября”;
В=“Венера-планета”;
С=“На улице идет снег”.
Когда истинно логическое отрицание (дизъюнкция, конъюнкция)?
А=“Сегодня 30 сентября”;
В=“Венера-планета”;
С=“На улице идет снег”.
Когда истинно логическое отрицание (дизъюнкция, конъюнкция)?
Слайд 3Таблицы истинности
Решение логических выражений принято оформлять в виде таблиц, в которых
по действиям показано, какие значения принимает логическое выражение при всех возможных наборах его переменных
Слайд 4Определение
Таблица истинности - это таблица, с помощью которой устанавливается истинностное значение
сложного высказывания при всех значениях входящих в него простых высказываний.
Слайд 5Для составления таблицы истинности необходимо:
Количество строк = 2n+1, где n —
количество переменных.
Количество столбцов = количество переменных + количество логических операций.
Установить последовательность выполнения логических операций.
Построить таблицу, указывая названия столбцов и возможные наборы значений исходных логических переменных.
Заполнить таблицу истинности по столбцам.
Количество столбцов = количество переменных + количество логических операций.
Установить последовательность выполнения логических операций.
Построить таблицу, указывая названия столбцов и возможные наборы значений исходных логических переменных.
Заполнить таблицу истинности по столбцам.
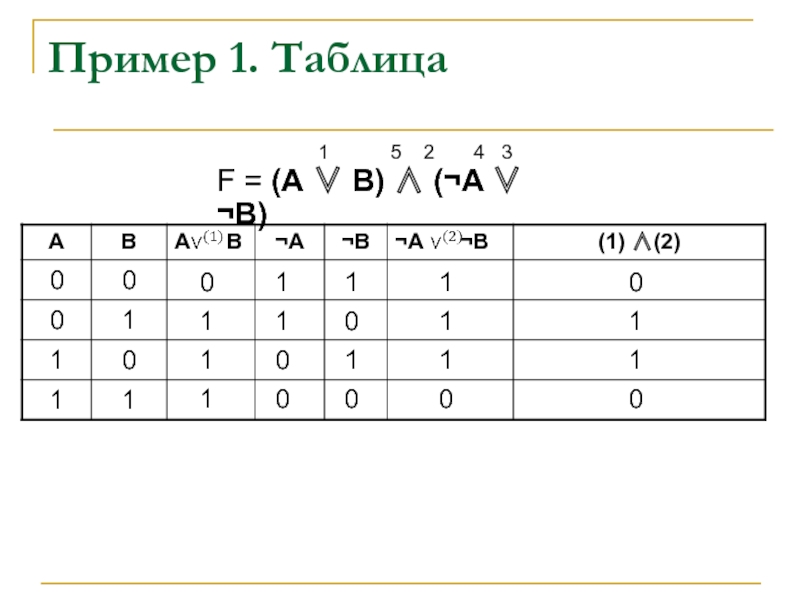
Слайд 6Пример 1
Построим таблицу истинности для функции
F = (А ∨ В)
∧ (¬A ∨ ¬B)
Переменных: две (А и В), т.е. N = 2 ⇒ количество строк: 2n=22=4. С заголовком: 5
Количество столбцов: 2 переменные + 5 операций (∨,∧,¬,∨ и ¬). Итого 7
Порядок операций:
1 5 2 4 3
F = (А ∨ В) ∧ (¬A ∨ ¬B)
Переменных: две (А и В), т.е. N = 2 ⇒ количество строк: 2n=22=4. С заголовком: 5
Количество столбцов: 2 переменные + 5 операций (∨,∧,¬,∨ и ¬). Итого 7
Порядок операций:
1 5 2 4 3
F = (А ∨ В) ∧ (¬A ∨ ¬B)
Слайд 8Пример 2
Построим таблицу истинности для функции
F = X ∨ Y
∧ ¬Z
Переменных:
три (X, Y и Z), т.е. n = 3 ⇒ количество строк: 2n=23=8. С заголовком: 9
Количество столбцов:
3 переменные + 3 операции (∨,∧,¬). Итого 6
Порядок операций:
3 2 1
F = X ∨ Y ∧ ¬Z
Переменных:
три (X, Y и Z), т.е. n = 3 ⇒ количество строк: 2n=23=8. С заголовком: 9
Количество столбцов:
3 переменные + 3 операции (∨,∧,¬). Итого 6
Порядок операций:
3 2 1
F = X ∨ Y ∧ ¬Z