- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Введение в математический анализ презентация
Содержание
- 1. Введение в математический анализ
- 2. Понятие функции. Способы задания функций Пусть X – некоторое множество действительных чисел.
- 3. Определение. Если каждому элементу x из множества
- 4. Множество X называется областью определения функции f(x)
- 5. Например, для функции y = sin x область определения D(f ) = R, область значений E(f ) = [–1; 1].
- 6. Различают следующие способы задания функции: табличный, графический, аналитический (с помощью формул).
- 7. Под графиком функции понимают множество точек плоскости,
- 8. К основным элементарным функциям относятся: y = xa (при
- 9. y = sin x, y = cos x, y = tg x, y = ctg x – тригонометрические функции; y = arcsin x, y = arccos x, y = arctg x, y = arcctg x – обратные тригонометрические функции.
- 10. Функция, заданная последовательной цепью нескольких функций (y
- 11. Функции, образованные из основных элементарных функций посредством
- 12. Все остальные функции называются неэлементарными. Примером неэлементарной функции может служить функция вида
- 13. Функция, определяемая уравнениями в
- 14. Например, уравнения определяют линейную функцию
- 15. Предел числовой последовательности. Предел функции
- 16. Определение. Число A называется пределом последовательности
- 17. Если последовательность a1, a2, …an,… имеет своим
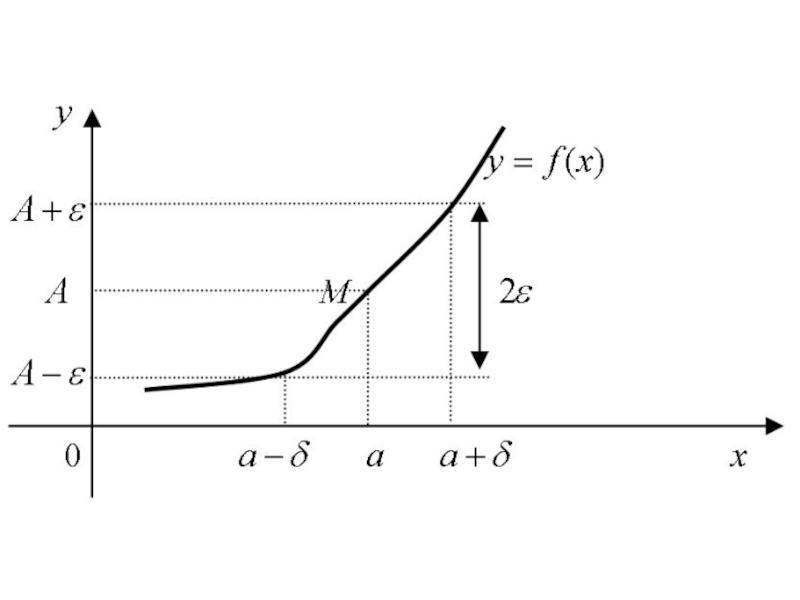
- 18. Определение. Число А называется пределом функции y = f(x)
- 19. Обозначают этот факт так:
- 20. Если число A является пределом функции y = f(x)
- 21. Так как из неравенства 0
- 23. Число A называется пределом функции y = f(x) при
- 24. Функция y = f(x) называется ограниченной в области D,
- 25. Например, функция ограничена
- 26. Бесконечно малые и бесконечно большие функции
- 27. Определение. Функция α(x) называется бесконечно малой при
- 28. Например, функция y = sin x является бесконечно малой при
- 29. Теорема. Если функция α(x) – бесконечно малая
- 30. Если функция β(x) – бесконечно большая при
- 31. Справедливы следующие утверждения: Сумма конечного числа бесконечно малых функций есть бесконечно малая функция.
- 32. Произведение ограниченной функции на бесконечно малую есть
- 33. Теоремы о пределах Если пределы
- 34. 1) где с = const; 2)
- 35. 3) 4) где
- 36. Замечательные пределы Первый замечательный предел:
- 37. Второй замечательный предел:
- 38. Функция y = ex = exp(x) называется экспонентой; y = loge x = ln x называется натуральным логарифмом.
- 39. Пример. Вычислить
- 40. Решение.Так как то
- 41. Пример. Вычислить
- 42. Решение. Так как при x → ∞ числитель и
- 43. Для раскрытия таких неопределенностей делят числитель и
- 45. Пример. Вычислить
- 46. Решение. Так как то имеем неопределённость вида
- 47. Так как, то
- 48. Пример. Вычислить
- 49. Решение. Имеем неопределенность вида Умножим числитель и
- 52. Пример. Вычислить
- 53. Решение. Для раскрытия неопределённости воспользуемся первым замечательным
- 55. Пример. Вычислить
- 56. Решение. Для раскрытия неопределённости 1∞ воспользуемся вторым замечательным пределом:
- 57. поскольку
- 58. Сравнение бесконечно малых функций Для сравнения двух
- 59. Если A ≠ 0 и A ≠ ∞, то функции α(x)
- 60. Если A = 1, то бесконечно малые функции α(x)
- 61. Основные эквивалентности при x → 0: sin kx ~ kx,
- 62. При вычислении пределов используют следующую теорему. Теорема.
- 63. Пример. Вычислить
- 64. Решение. Воспользуемся эквивалентными бесконечно малыми функциями. Так
- 66. Сравнение бесконечно малых функций Для сравнения
- 67. Если A ≠ 0 и A ≠ ∞, то функции α(x)
- 68. Если A = 1, то бесконечно малые функции α(x)
- 69. Основные эквивалентности при x → 0: sin kx ~ kx,
- 70. При вычислении пределов используют следующую теорему. Теорема.
- 71. Пример. Вычислить
- 72. Решение. Воспользуемся эквивалентными бесконечно малыми функциями. Так
- 74. Непрерывность функции Определение. Функция y = f(x) называется
- 75. Односторонними называются пределы: левосторонний предел в точке
- 76. Определение. Функция y = f(x) называется непрерывной в точке
- 77. Если односторонние пределы конечны, но нарушается хотя
- 78. Если хотя бы один из этих односторонних
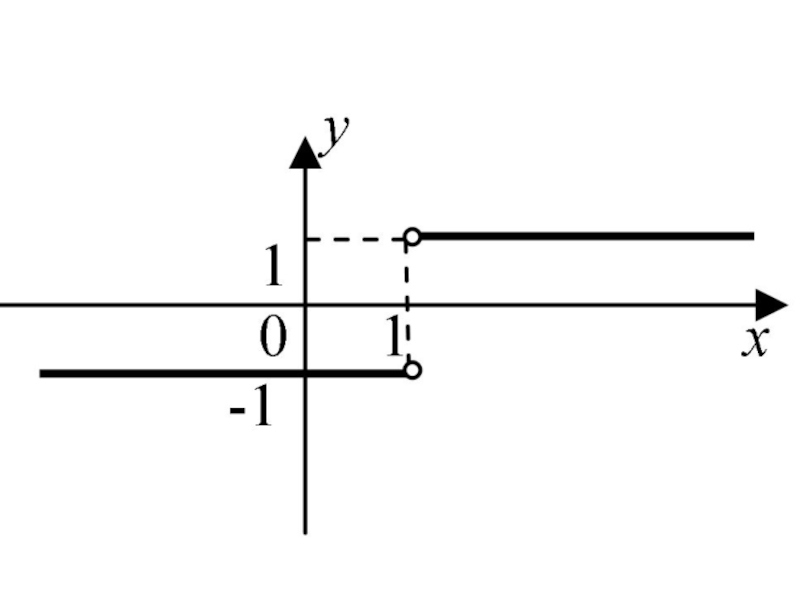
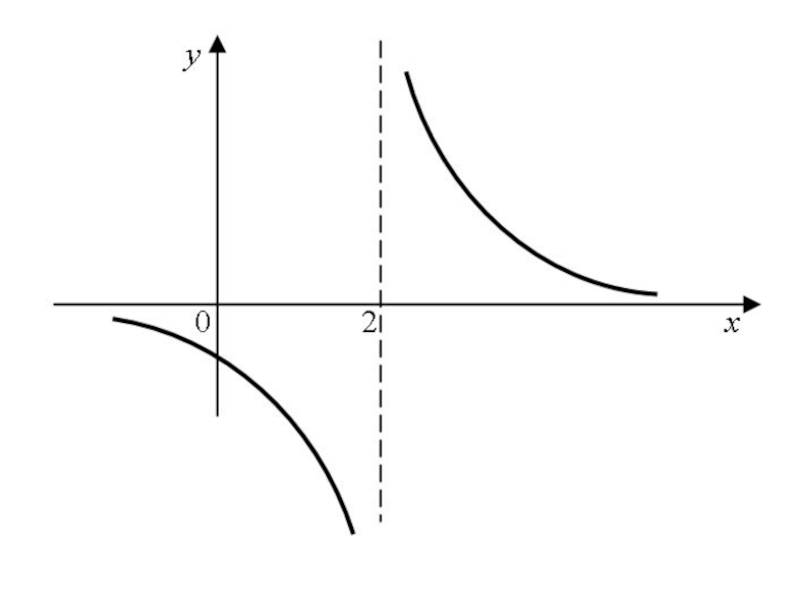
- 79. Например, функция
- 81. Функция имеет в точке x = 2 разрыв второго рода
- 83. Если функция непрерывна во всех точках отрезка
- 84. Из определения непрерывности функции и теорем о
- 85. II. Сложная функция, составленная из непрерывных функций,
Слайд 3Определение. Если каждому элементу x из множества X по некоторому закону
Слайд 4Множество X называется областью определения функции f(x) и обозначается D(f ).
Слайд 5Например, для функции y = sin x область определения D(f ) = R, область
Слайд 6Различают следующие способы задания функции: табличный, графический, аналитический (с помощью формул).
Слайд 7Под графиком функции понимают множество точек плоскости, абсциссы которых есть значения
Слайд 8К основным элементарным функциям относятся:
y = xa (при постоянном a ∊ R) – степенная функция;
y = ax
y = loga x (при постоянном a ∊ R, a > 0, a ≠ 1) – логарифмическая функция;
Слайд 9y = sin x, y = cos x, y = tg x, y = ctg x – тригонометрические функции;
y = arcsin x, y = arccos x, y = arctg x, y = arcctg x – обратные тригонометрические
Слайд 10Функция, заданная последовательной цепью нескольких функций (y = f(u), где u
Слайд 11Функции, образованные из основных элементарных функций посредством конечного числа алгебраических операций
Слайд 12Все остальные функции называются неэлементарными. Примером неэлементарной функции может служить функция
Слайд 13Функция, определяемая уравнениями
в которых зависимость между y и x
Слайд 16Определение. Число A называется пределом последовательности
a1, a2, …,an,…, если
Слайд 17Если последовательность a1, a2, …an,… имеет своим пределом число A, то
или
Слайд 18Определение. Число А называется пределом функции y = f(x) при x → a (в точке
Слайд 20Если число A является пределом функции y = f(x) при x → a, то на
Слайд 21Так как из неравенства 0
Слайд 23Число A называется пределом функции y = f(x) при x → ±∞, если для любого
Слайд 24Функция y = f(x) называется ограниченной в области D, если существует постоянное число
Слайд 27Определение. Функция α(x) называется бесконечно малой при x → a, если
Функция β(x)
Слайд 28Например, функция y = sin x является бесконечно малой при x → 0, а функция
Слайд 29Теорема. Если функция α(x) – бесконечно малая при x → a, то
Слайд 31Справедливы следующие утверждения:
Сумма конечного числа бесконечно малых функций есть бесконечно малая
Слайд 32Произведение ограниченной функции на бесконечно малую есть бесконечно малая функция.
Произведение конечного
Слайд 37Второй замечательный предел:
где e — иррациональное число, e ≈ 2,718281828 — одна
Слайд 38Функция y = ex = exp(x) называется экспонентой; y = loge x = ln x называется натуральным логарифмом.
Слайд 42Решение. Так как при x → ∞ числитель и знаменатель дроби, стоящей под
Слайд 43Для раскрытия таких неопределенностей делят числитель и знаменатель дроби на старшую
Слайд 49Решение. Имеем неопределенность вида Умножим числитель и знаменатель дроби на выражение
Слайд 53Решение. Для раскрытия неопределённости воспользуемся первым замечательным пределом. Считая, что x ≠ 0,
Слайд 58Сравнение бесконечно малых функций
Для сравнения двух бесконечно малых функций α(x) и
Слайд 59Если A ≠ 0 и A ≠ ∞, то функции α(x) и β(x) называются бесконечно
Если A = 0, то α(x) называется бесконечно малой высшего порядка по сравнению с β(x). Записывается это так: α(x) = o(β(x)).
Слайд 60Если A = 1, то бесконечно малые функции α(x) и β(x) называют эквивалентными
Слайд 61Основные эквивалентности при x → 0:
sin kx ~ kx, tg kx ~ kx,
arcsin kx ~ kx,
ln (1+kx) ~ kx, ekx – 1 ~ kx.
Слайд 62При вычислении пределов используют следующую теорему.
Теорема. Предел отношения двух бесконечно малых
Слайд 64Решение. Воспользуемся эквивалентными бесконечно малыми функциями. Так как при x → 0
и sin 3x ~ 3x, то
Слайд 66Сравнение бесконечно малых функций
Для сравнения двух бесконечно малых функций α(x)
Слайд 67Если A ≠ 0 и A ≠ ∞, то функции α(x) и β(x) называются бесконечно
Если A = 0, то α(x) называется бесконечно малой высшего порядка по сравнению с β(x). Записывается это так: α(x) = o(β(x)).
Слайд 68Если A = 1, то бесконечно малые функции α(x) и β(x) называют эквивалентными
Слайд 69Основные эквивалентности при x → 0:
sin kx ~ kx, tg kx ~ kx,
arcsin kx ~ kx,
ln (1+kx) ~ kx, ekx – 1 ~ kx.
Слайд 70При вычислении пределов используют следующую теорему.
Теорема. Предел отношения двух бесконечно малых
Слайд 72Решение. Воспользуемся эквивалентными бесконечно малыми функциями. Так как при x → 0
и sin 3x ~ 3x, то
Слайд 74Непрерывность функции
Определение. Функция y = f(x) называется непрерывной в точке x = x0, если
Слайд 75Односторонними называются пределы:
левосторонний предел в точке a:
правосторонний предел в точке a:
Слайд 76Определение. Функция y = f(x) называется непрерывной в точке x = x0, если существуют односторонние
Слайд 77Если односторонние пределы конечны, но нарушается хотя бы одно из равенств
то x0 называется точкой разрыва 1-го рода.
Слайд 78Если хотя бы один из этих односторонних пределов не существует или
Слайд 83Если функция непрерывна во всех точках отрезка [a; b], то она называется
Слайд 84Из определения непрерывности функции и теорем о пределах следуют теоремы:
I. Если




![Например, для функции y = sin x область определения D(f ) = R, область значений E(f ) = [–1; 1].](/img/tmb/6/501311/5332392214524498ca6bded20bd66025-800x.jpg)








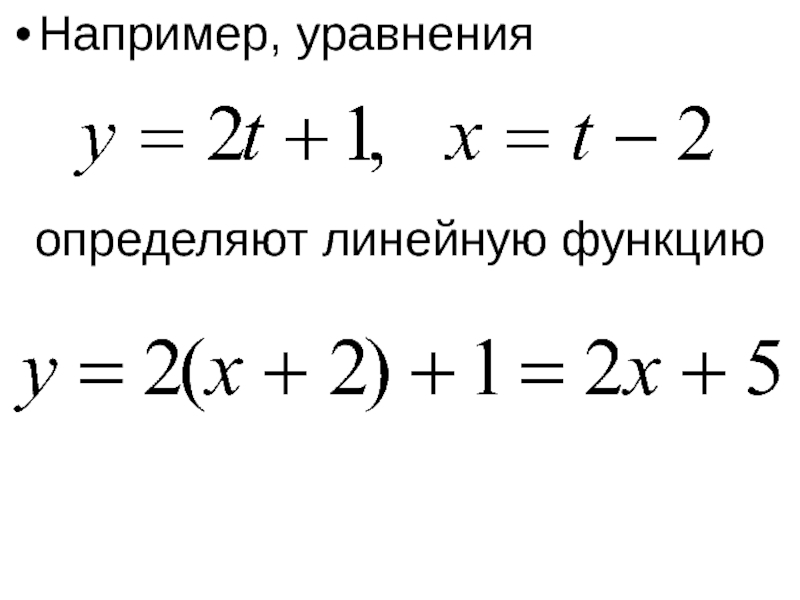


















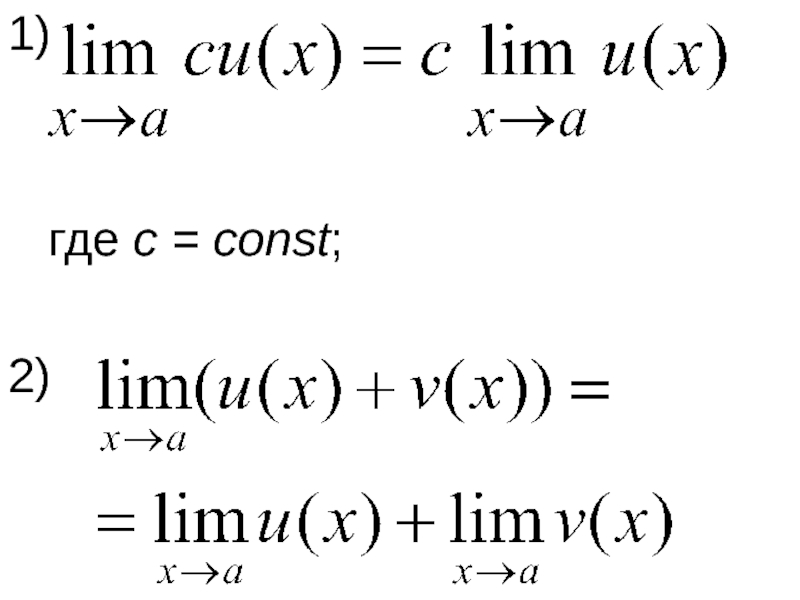
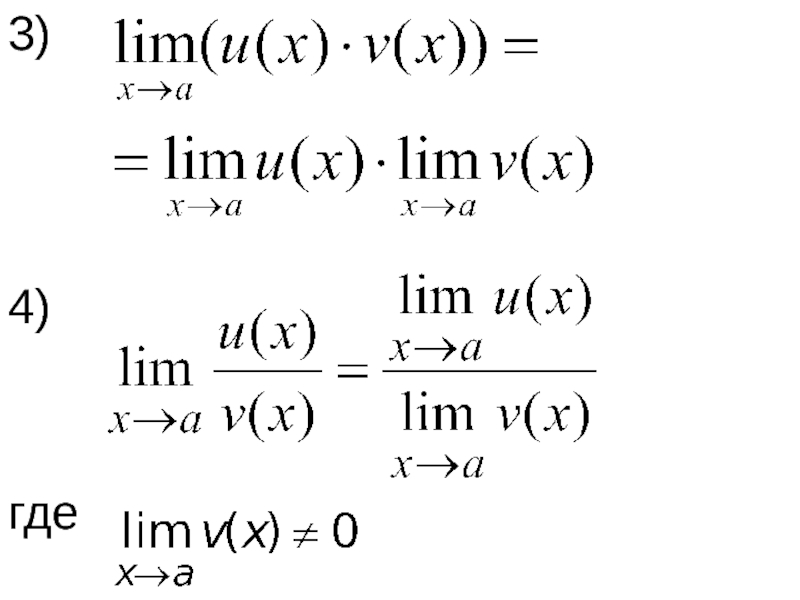
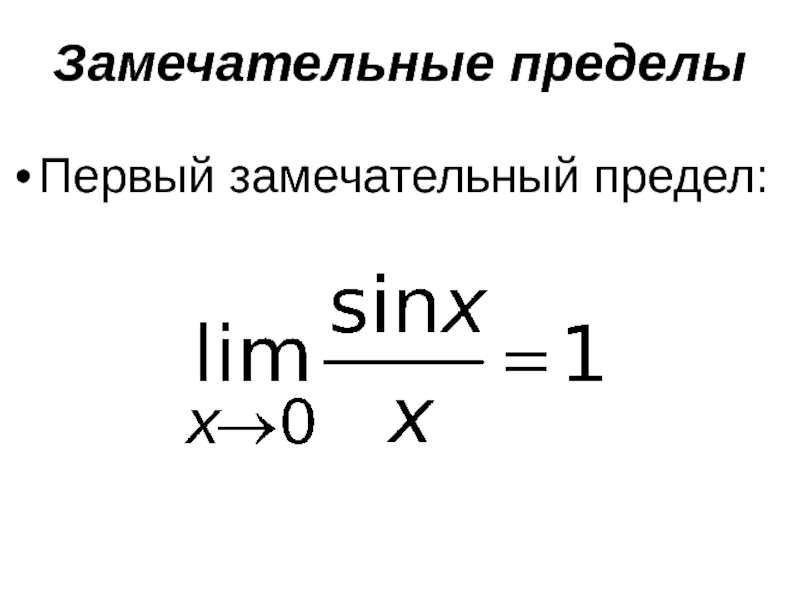


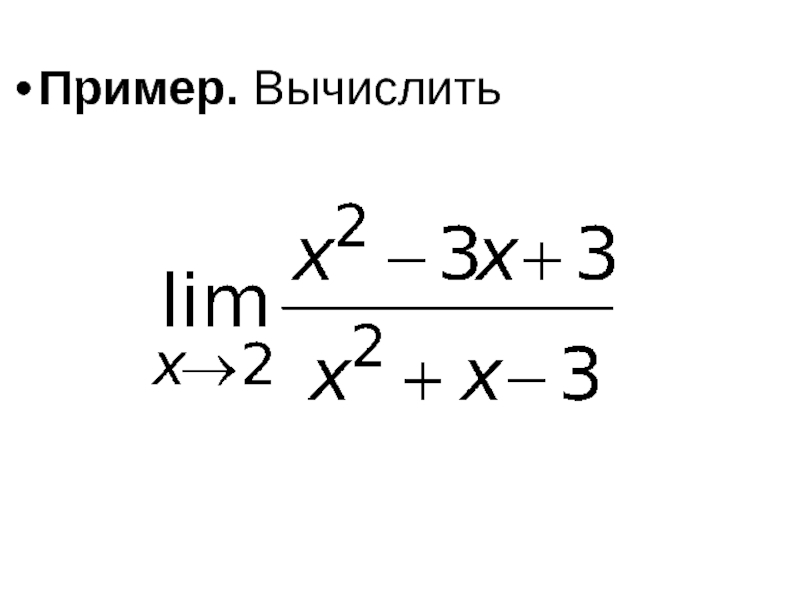

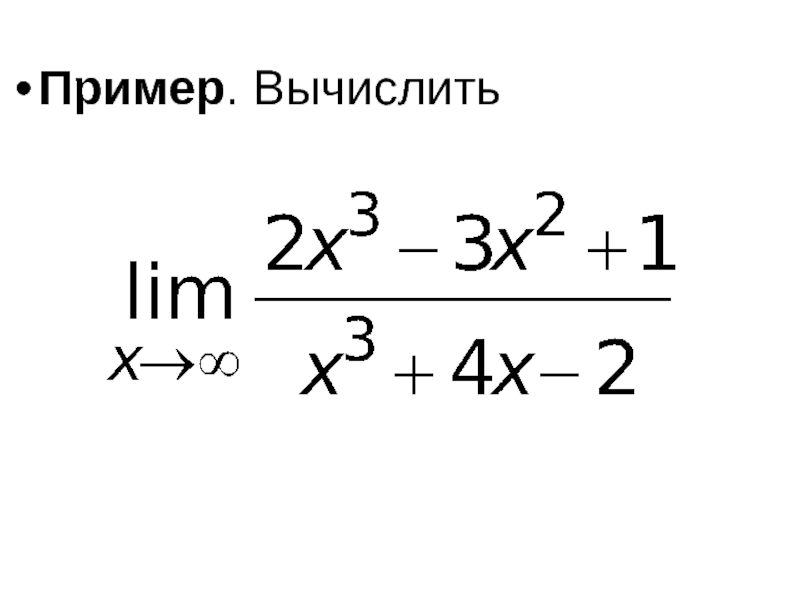


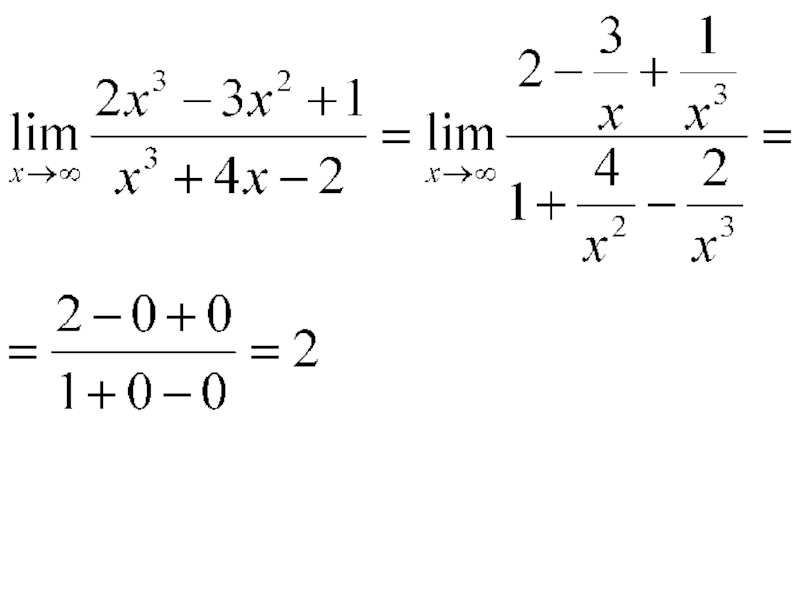
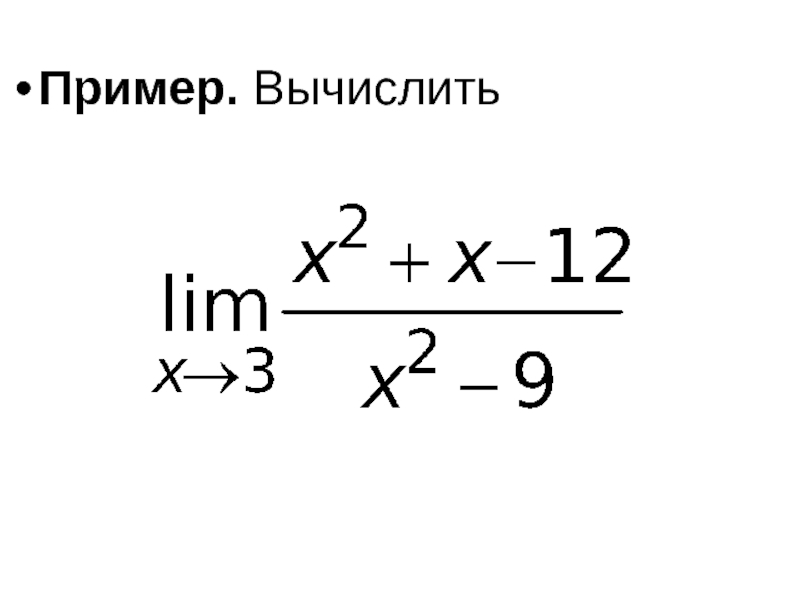
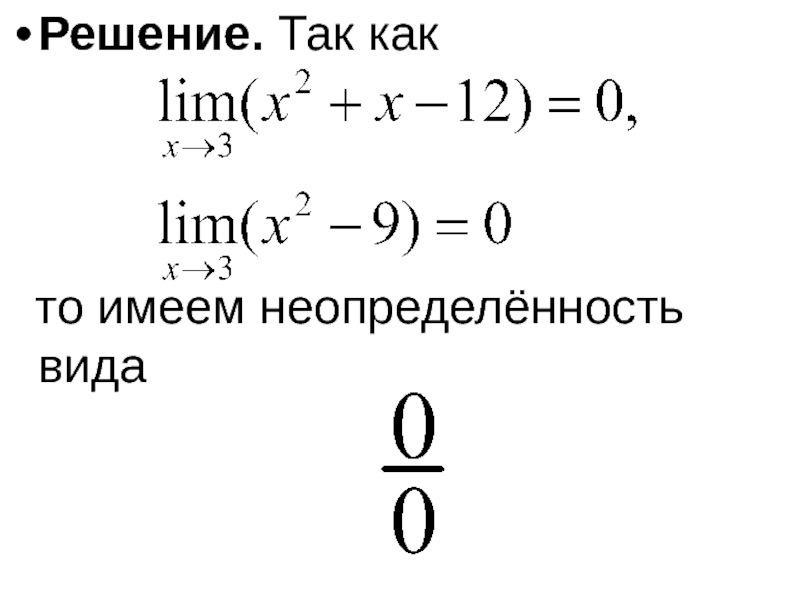
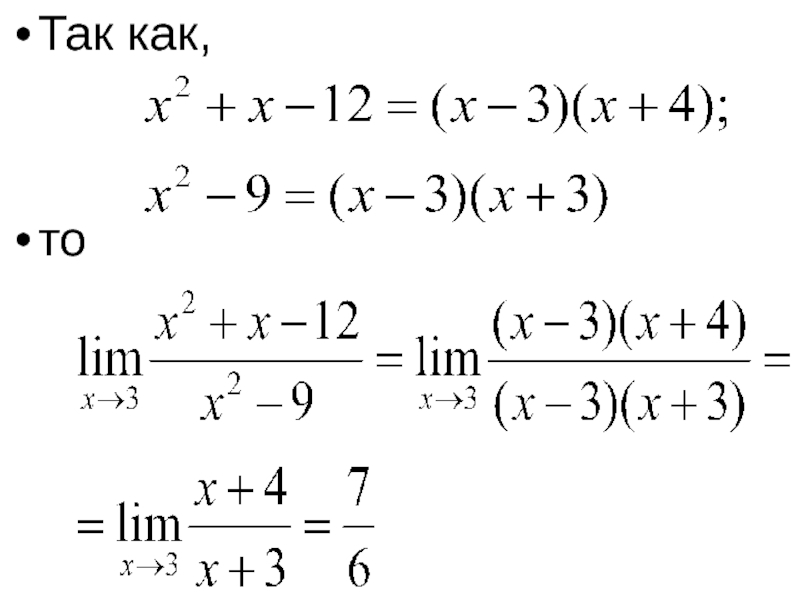
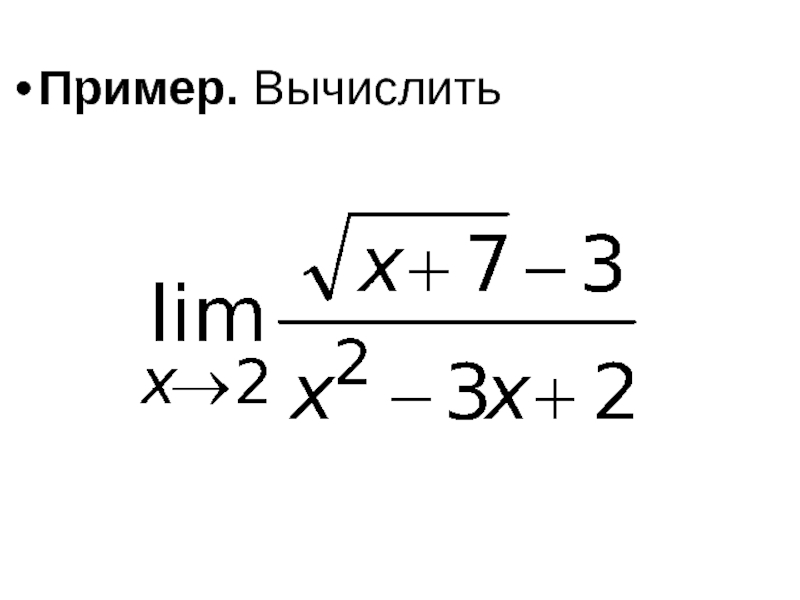

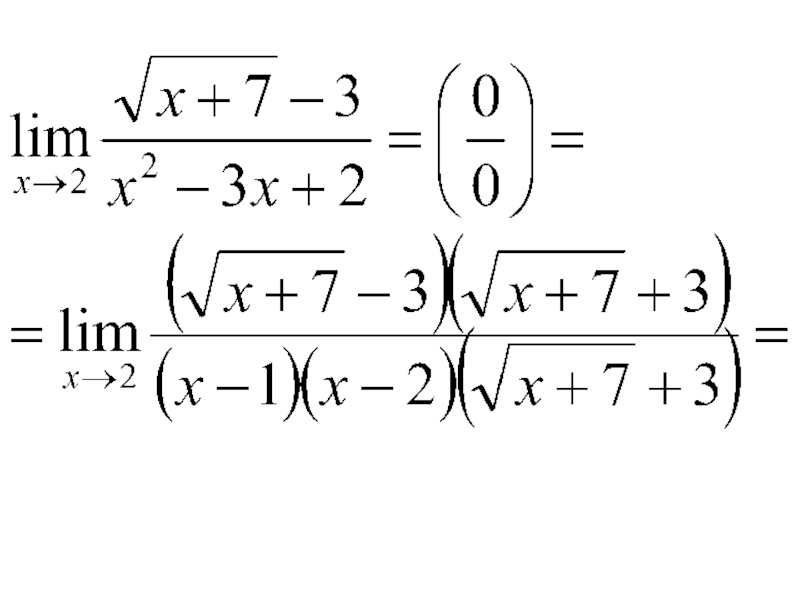
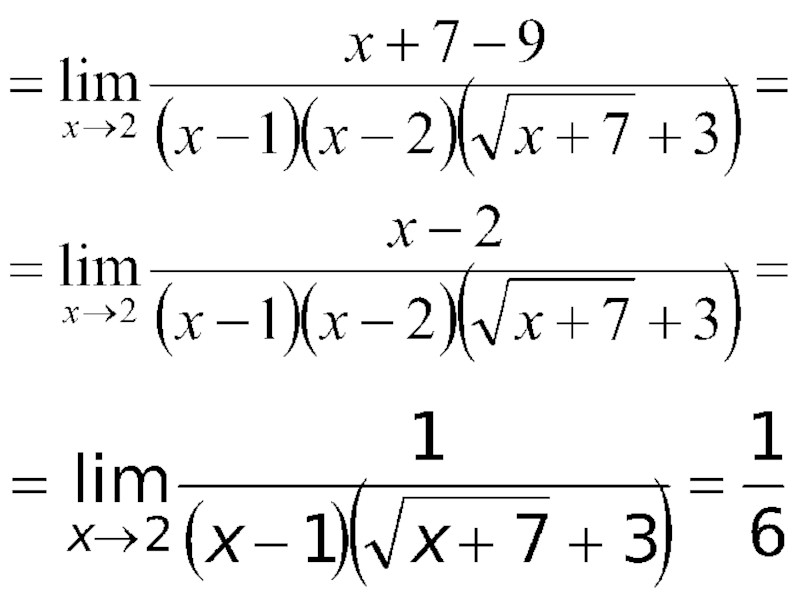
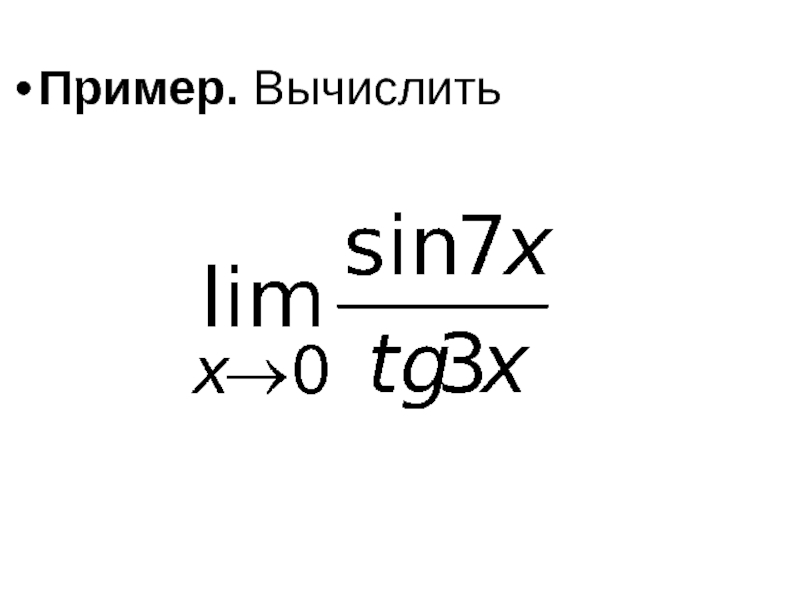

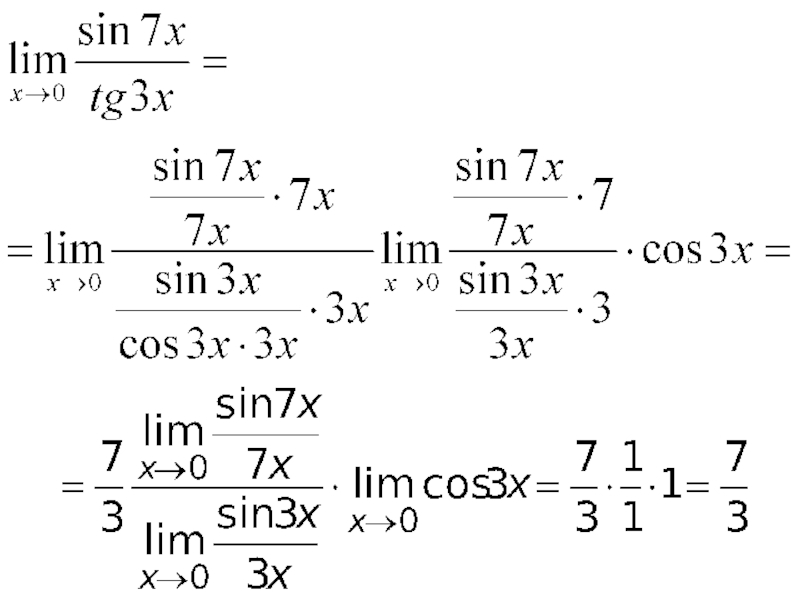
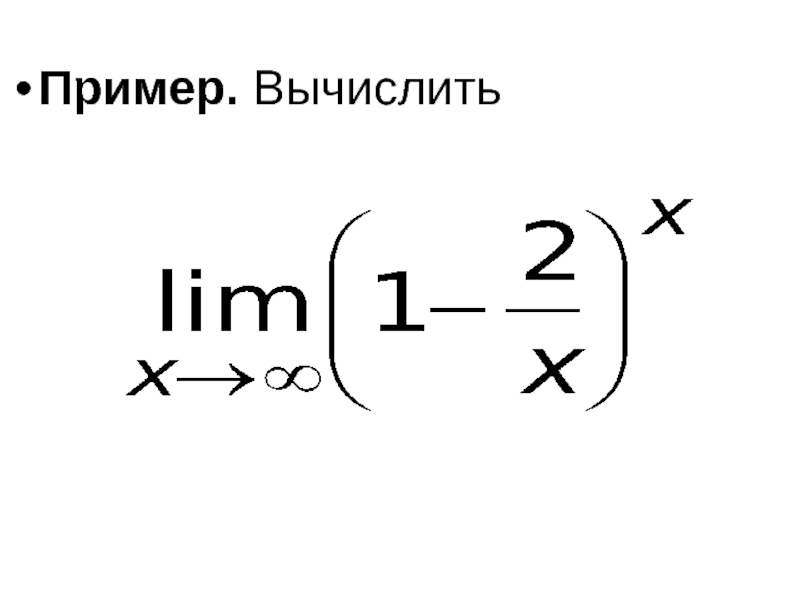

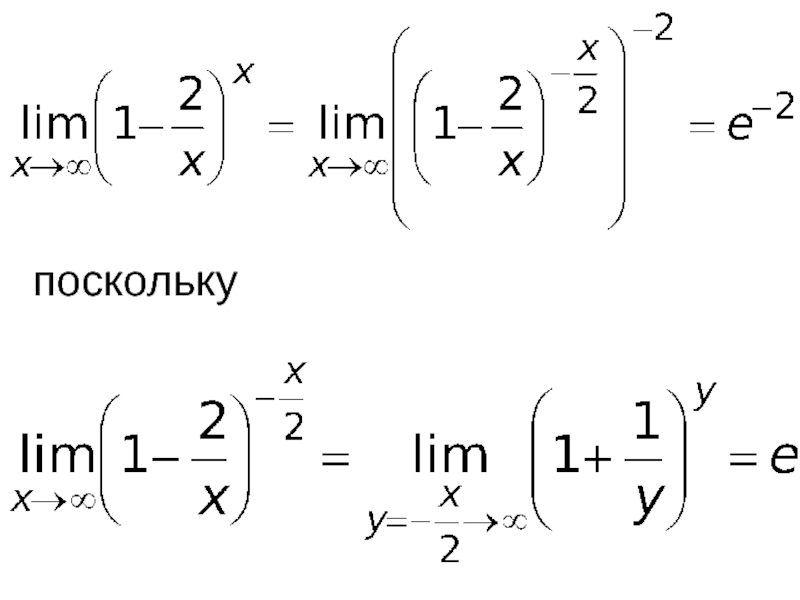





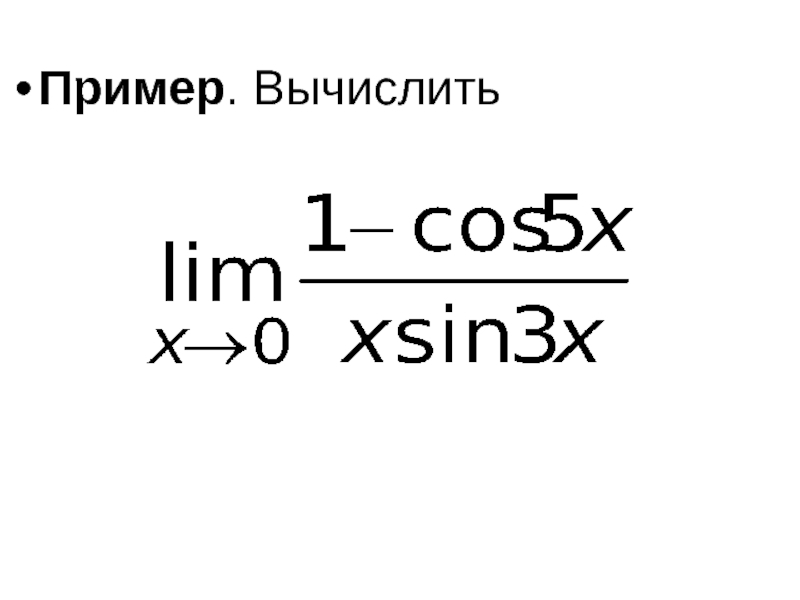

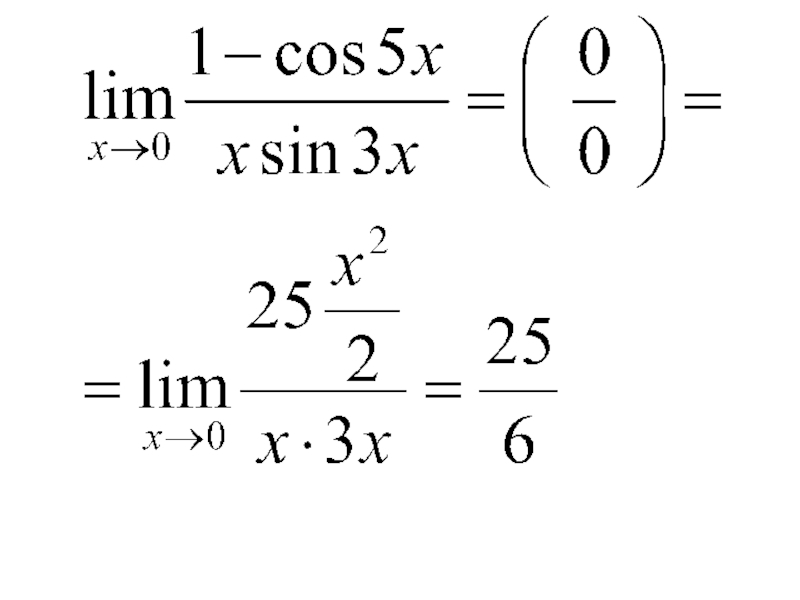


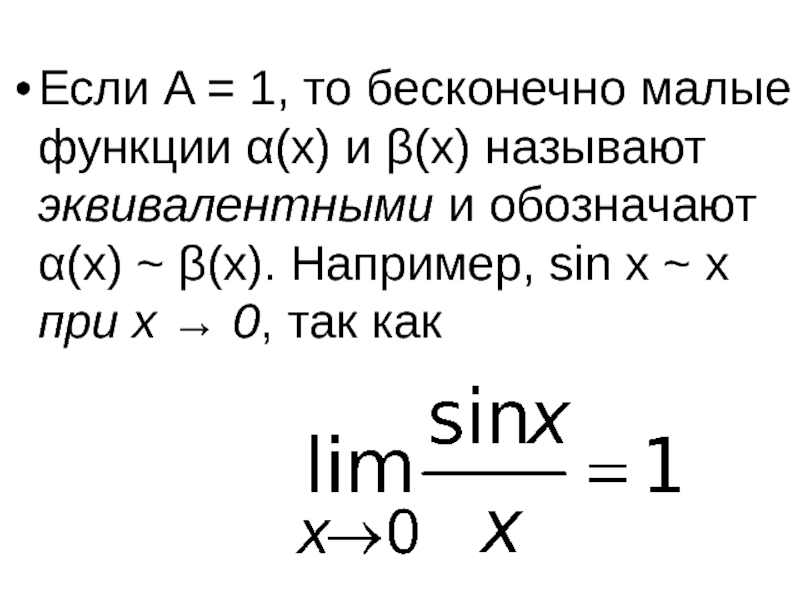


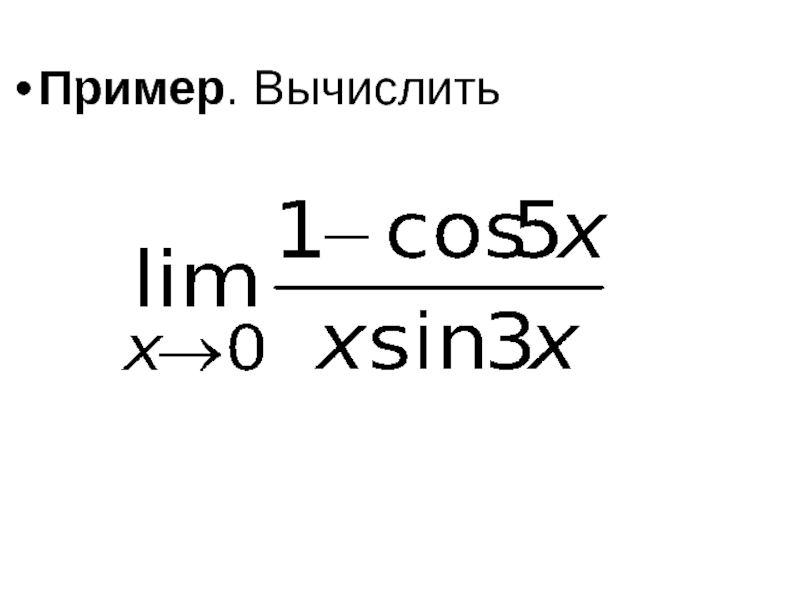

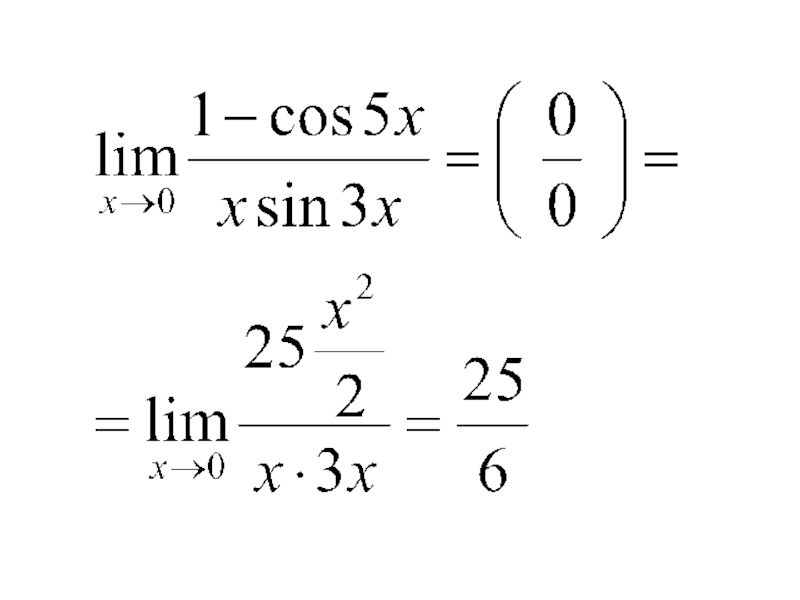







![Если функция непрерывна во всех точках отрезка [a; b], то она называется непрерывной на этом отрезке.](/img/tmb/6/501311/dc2e5ef6a6881ef37ce6b474faccf080-800x.jpg)







