- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Введение в асимптотические методы. Лекция 4. Интегралы: нелокальные вклады презентация
Содержание
- 1. Введение в асимптотические методы. Лекция 4. Интегралы: нелокальные вклады
- 2. 1. Локальные и глобальные вклады До сих
- 3. 2. Пример 1 Оценим, как произведение
- 4. 3. Пример 1: метод вычитания Локальный вклад
- 5. 4. Пример 1: метод расщепления Иной подход
- 6. 5. Пример 1: метод расщепления Для вычисления
- 7. 6. Пример 2 Локальный вклад Глобальный вклад
- 8. 7. Пример 2 :метод расщепления + Метод
- 9. 8. Пример 3: Логарифмы Наиболее сложна промежуточная
- 10. 9. Интегральное уравнение: Электрическая емкость тонкого тела
- 11. 10. Интегральное уравнение: оценка интегралов В первую
- 12. 11. Интегральное уравнение: итерации
- 13. 12. Интегральное уравнение: эллипсоиды
- 14. Из проведенного исследования следуют два интересных физических
- 15. Вычислить первые два члена при
Слайд 21. Локальные и глобальные вклады
До сих пор мы рассматривали интегралы, подобные
Это, конечно, не есть общее правило.
Возможны ситуации, когда главный, либо следующие члены асимптотического разложения, определяются вкладом всего интервала интегрирования. Соответствующие вклады мы будем называть глобальными, в отличие от локальных вкладов из малых областей интервала интегрирования.
В данной лекции на простых примерах рассматривается техника выделения различных вкладов.
Слайд 32. Пример 1
Оценим, как произведение величины функции на длину интервала, вклад
главный член дается глобальным вкладом, когда подынтегральная функция может быть аппроксимирована как , а интервал интегрирования расположен между единицей и малой величиной, находящейся вне -окрестности нуля.
Слайд 43. Пример 1: метод вычитания
Локальный вклад
Глобальный вклад
Как искать следующие члены разложения?
Победа локального.
- перенормировка
С ростом числа удерживаемых в асимптотическом разложении членов метод вычитания становится все более трудоемким
Слайд 54. Пример 1: метод расщепления
Иной подход основан на предварительном нахождении внешнего
Внешнее разложение
Внутреннее разложение
Расщепляем интеграл на два
Слайд 65. Пример 1: метод расщепления
Для вычисления I2 используем внешнее разложение
Для вычисления
Складывая их, получим четыре главных члена АР
Подчеркнем, что все содержащие члены в разложениях должны были сократиться и сократились при суммировании.
Слайд 76. Пример 2
Локальный вклад
Глобальный вклад
Поправочный член приходит от глобального вклада
Можно
Другая возможность:
Этот интеграл расходится из-за поведения на , т.е. вовне интервала
Это указывает на глобальность вклада в поправочном члене.
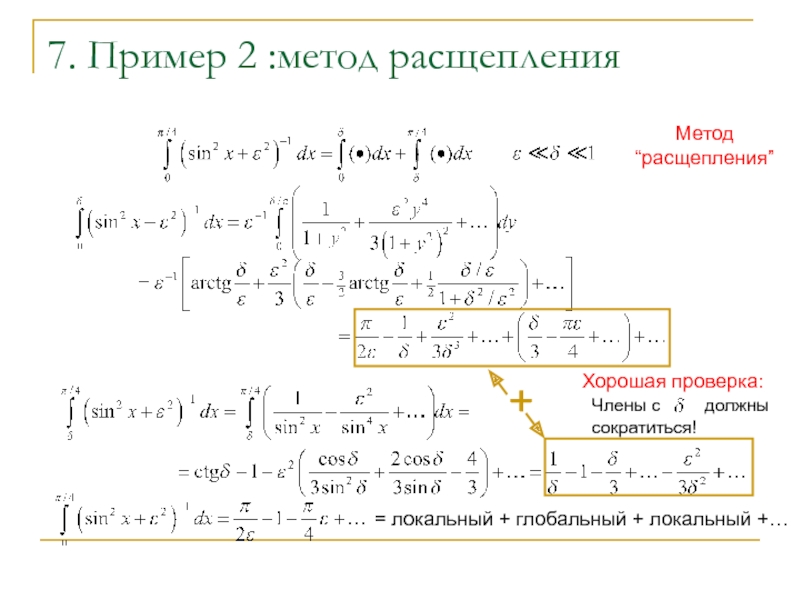
Слайд 87. Пример 2 :метод расщепления
+
Метод “расщепления”
Хорошая проверка:
Члены с
сократиться!
Слайд 98. Пример 3: Логарифмы
Наиболее сложна промежуточная ситуация – когда основной вклад
Победа глобального
Победа локального
Локальный вклад
Нелокальный вклад
Ничья
Здесь основной вклад – из зазора
Слайд 109. Интегральное уравнение: Электрическая емкость тонкого тела
Для нахождения электрической емкости
(1)
необходимо
Интегральные уравнения требуют привлечения как техники решения алгебраических уравнений, так и техники асимптотического анализа интегралов
Слайд 1110. Интегральное уравнение: оценка интегралов
В первую очередь нужно асимптотически исследовать интеграл
Слайд 1211. Интегральное уравнение: итерации
Чтобы найти следующие члены разложения удобно воспользоваться методом
Слайд 1312. Интегральное уравнение: эллипсоиды
Здесь, по существу, нам удалось полностью просуммировать ряд
принципиально улучшив таким образом асимптотическое разложение
(1)
Слайд 14Из проведенного исследования следуют два интересных физических феномена.
Слабая зависимость емкости
Емкость длинного тонкого тела оказывается аномально большой по сравнению с телами, имеющими размеры одного порядка по всем направлениям. К примеру шар того же объема ( ) имеет емкость (пропорциональную радиусу) , что много меньше емкости длинного тонкого тела
13. Интегральное уравнение: выводы
Фильтрационная аналогии: скважина намного лучше, чем сферическая полость того же объема. Правда еще лучше тонкое блинообразное тело того же объема. Попробуйте проверить!
Слайд 15Вычислить первые два члена при и
Рассмотреть интеграл
Найти 2 члена асимптотического разложения при эллиптического интеграла
Функция удовлетворяет интегральному уравнению
14. Упражнения к лекции 4
Найти два главных члена ее асимптотического представления