- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Вписанная окружность презентация
Содержание
- 1. Вписанная окружность
- 2. ЦЕЛИ УРОКА: 1.Познакомится с определением вписанной окружности.
- 3. Так четырехугольник EFNM описан около окружности, а
- 4. В любой треугольник можно вписать окружность. Т е о р е м а:
- 5. Д а н о: ∆ ABC. Док-ть:
- 6. ЗАМЕЧАНИЯ: В треугольник можно вписать только
- 7. Домашняя работа : 1. Что называется
Слайд 2ЦЕЛИ УРОКА:
1.Познакомится с определением вписанной окружности.
2.Изучить доказательство теоремы о вписанной
3.Решение задач по данной теме.
Слайд 3Так четырехугольник EFNM описан около окружности, а четырехугольник NMКD не является
Опр-е: Если все стороны многоугольника касаются окружности , то окружность называется в п и с а н н о й в многоугольник , а многоугольник – о п и с а н н ы м около этой окружности.
E
F
D
K
M
N
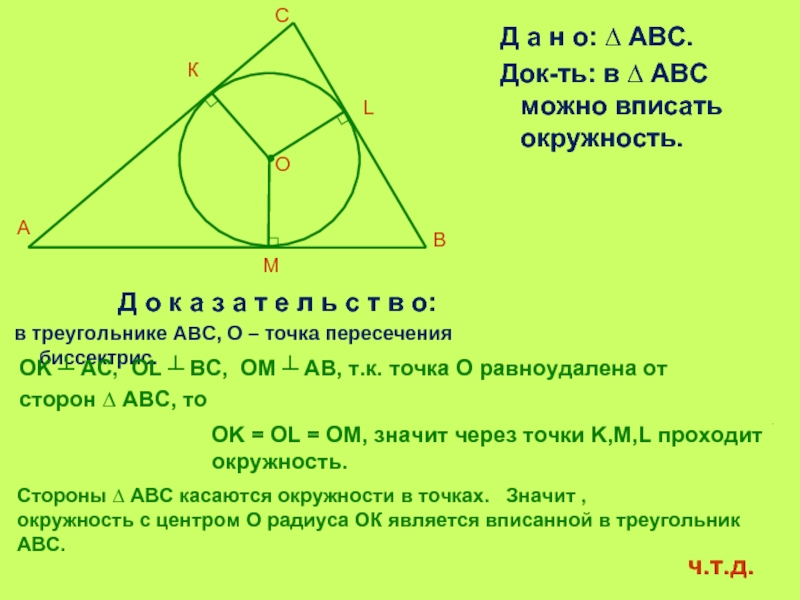
Слайд 5Д а н о: ∆ ABC.
Док-ть: в ∆ АВС можно вписать
Д о к а з а т е л ь с т в о:
в треугольнике ABC, О – точка пересечения биссектрис.
OK ┴ AС, OL ┴ BC, OM ┴ AB, т.к. точка О равноудалена от
сторон ∆ АВС, то
Стороны ∆ ABC касаются окружности в точках. Значит ,
окружность с центром О радиуса ОК является вписанной в треугольник АВС.
ч.т.д.
А
В
С
О
К
L
M
OK = OL = OM, значит через точки K,M,L проходит окружность.
Слайд 6ЗАМЕЧАНИЯ:
В треугольник можно вписать только одну окружность.
2. Не во всякий четырехугольник
3. В любом описанном четырехугольнике суммы противоположных сторон равны.
4. Если суммы противоположных сторон выпуклого четырехугольника равны, то в него можно вписать окружность.
Слайд 7Домашняя работа :
1. Что называется вписанной окружностью?
2. Что является центром вписанной
3. В любой ли треугольник можно вписать окружность?
Вопросы для повторения:
§ 74. № 690 , №693(а).