- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Вписанная и описанная окружности презентация
Содержание
- 1. Вписанная и описанная окружности
- 2. Определение. Окружность называется вписанной в многоугольник, если
- 3. Обратно: Если суммы противоположных сторон
- 4. Замечание 1. Если в прямоугольник
- 5. Определение. Окружность называется oписанной около многоугольника, если
- 6. Обратное: Если сумма противоположных углов четырехугольника равна
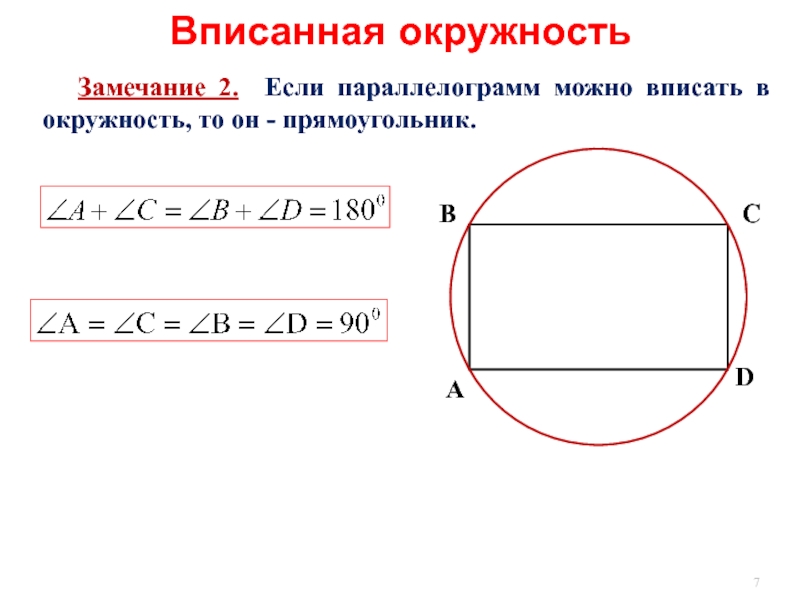
- 7. Замечание 2. Если параллелограмм можно
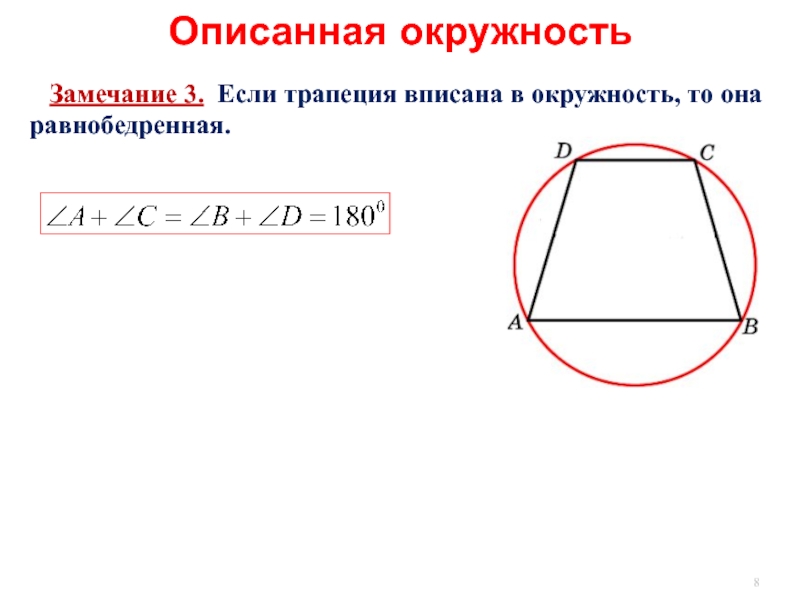
- 8. Описанная окружность Замечание 3. Если трапеция вписана в окружность, то она равнобедренная.
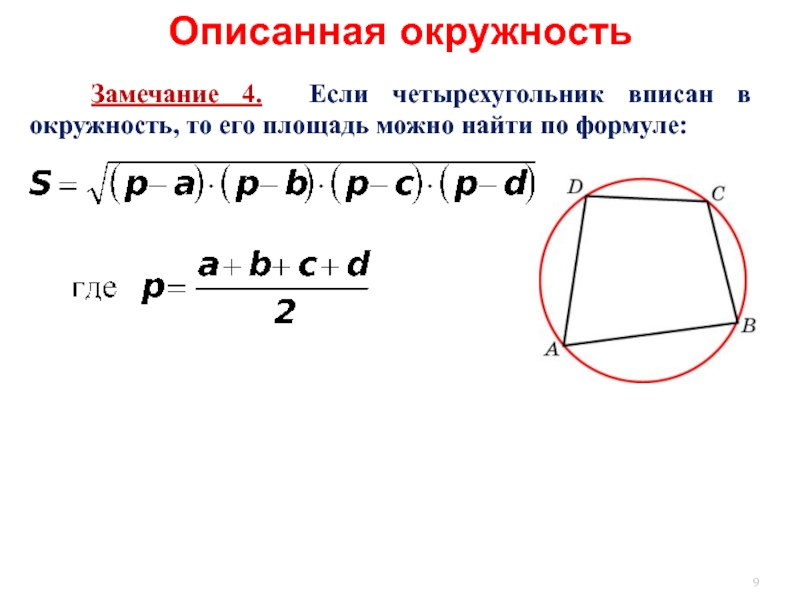
- 9. Описанная окружность Замечание 4. Если
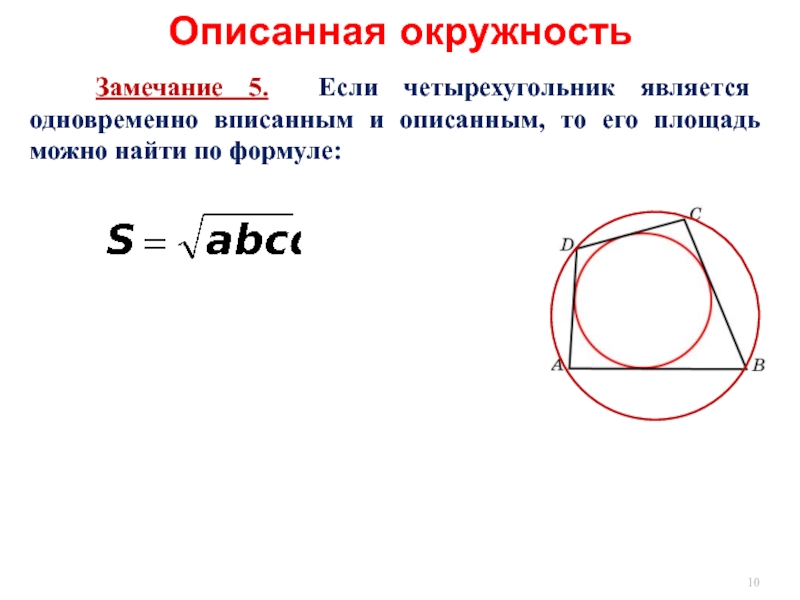
- 10. Описанная окружность Замечание 5.
- 11. Площадь треугольника, описанного около окружности выражается
- 12. Площадь
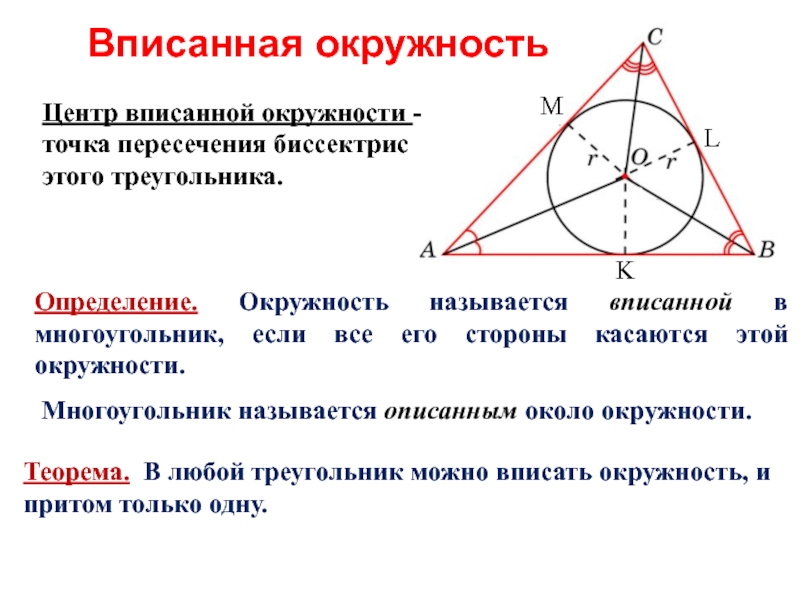
Слайд 2Определение. Окружность называется вписанной в многоугольник, если все его стороны касаются
Многоугольник называется описанным около окружности.
Теорема. В любой треугольник можно вписать окружность, и притом только одну.
Центр вписанной окружности - точка пересечения биссектрис этого треугольника.
Вписанная окружность
M
L
K
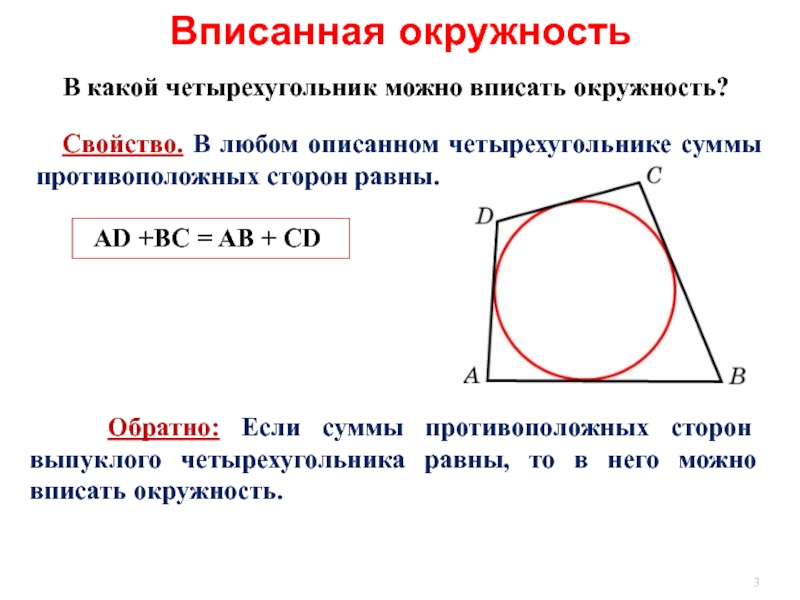
Слайд 3 Обратно: Если суммы противоположных сторон выпуклого четырехугольника равны, то
Свойство. В любом описанном четырехугольнике суммы противоположных сторон равны.
В какой четырехугольник можно вписать окружность?
AD +BC = AB + CD
Вписанная окружность
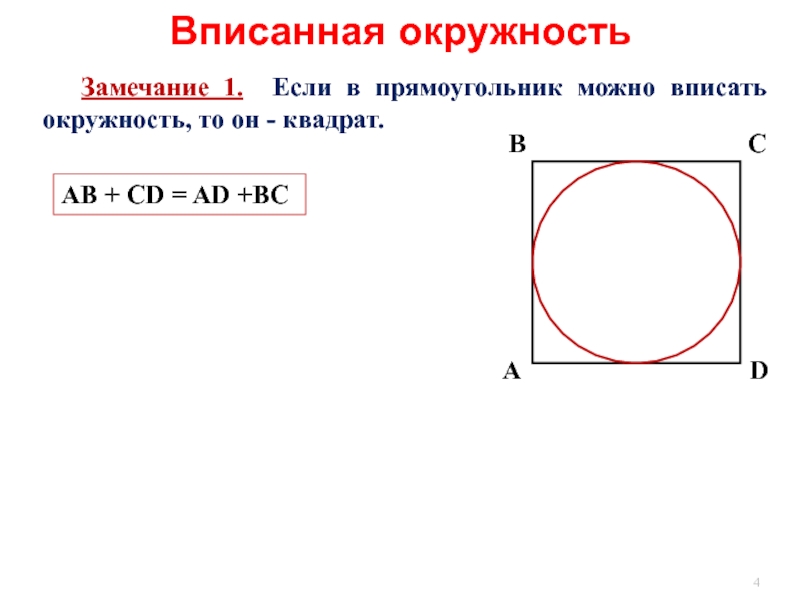
Слайд 4 Замечание 1. Если в прямоугольник можно вписать окружность, то
AB + CD = AD +BC
Вписанная окружность
А
С
В
D
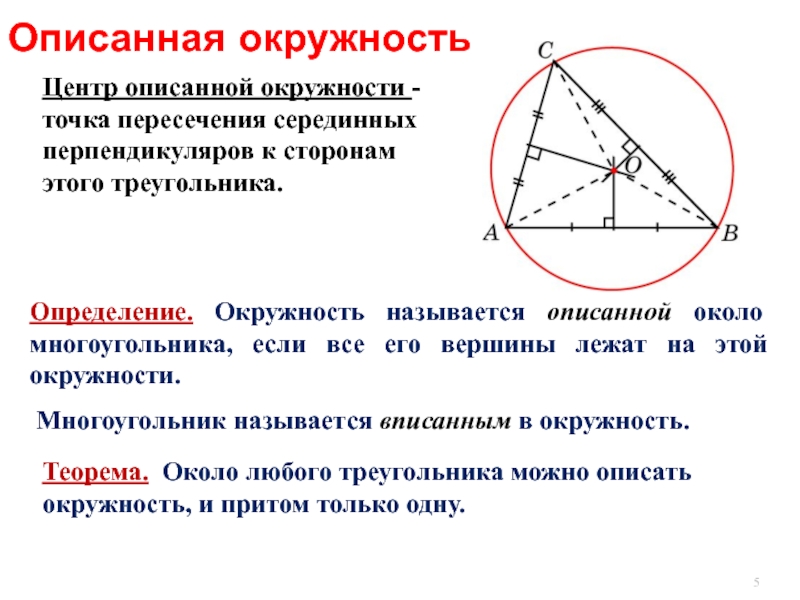
Слайд 5Определение. Окружность называется oписанной около многоугольника, если все его вершины лежат
Многоугольник называется вписанным в окружность.
Теорема. Около любого треугольника можно описать окружность, и притом только одну.
Центр описанной окружности - точка пересечения серединных перпендикуляров к сторонам этого треугольника.
Описанная окружность
Слайд 6Обратное: Если сумма противоположных углов четырехугольника равна 180о , то около
Всегда ли около четырехугольника можно описать окружность?
Свойство. В любом вписанном четырехугольнике сумма противоположных углов равна 1800.
Описанная окружность
Слайд 7 Замечание 2. Если параллелограмм можно вписать в окружность, то
Вписанная окружность
А
С
В
D
Слайд 9Описанная окружность
Замечание 4. Если четырехугольник вписан в окружность, то
Слайд 10Описанная окружность
Замечание 5. Если четырехугольник является одновременно вписанным и
Слайд 11Площадь треугольника, описанного
около окружности выражается формулой
где r – радиус вписанной
Р – периметр треугольника, S – его площадь.
Площадь треугольника, описанного около окружности
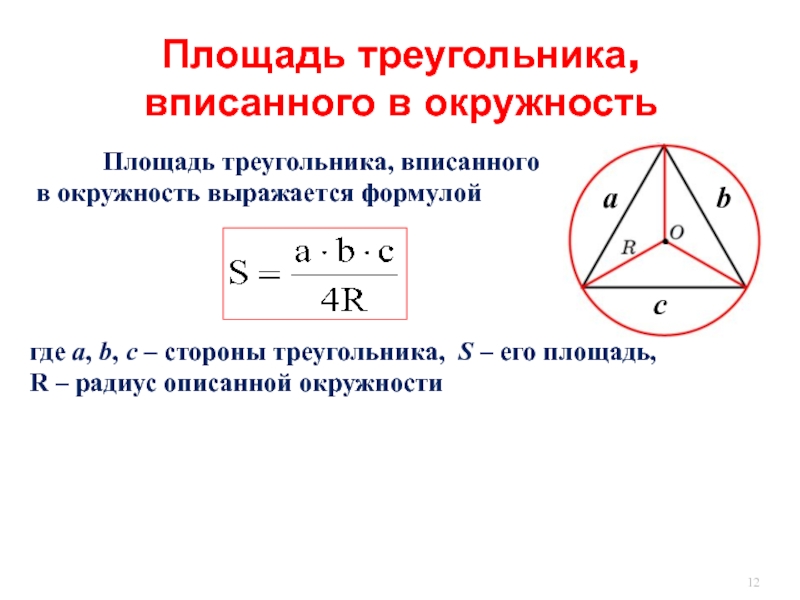
Слайд 12 Площадь треугольника, вписанного
в окружность
где a, b, c – стороны треугольника, S – его площадь,
R – радиус описанной окружности
Площадь треугольника, вписанного в окружность
b
а
c