- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Взаимное положение прямой и плоскости, двух плоскостей. Позиционные задачи. (Лекция 4) презентация
Содержание
- 1. Взаимное положение прямой и плоскости, двух плоскостей. Позиционные задачи. (Лекция 4)
- 2. Взаимное положение прямой и плоскости, двух плоскостей
- 3. Принадлежность прямой плоскости Прямая принадлежит плоскости, если
- 4. Параллельность прямой и плоскости Через точку
- 5. Параллельность прямой и плоскости Построим в плоскости
- 6. Параллельность прямой и плоскости Σ(Σ1, Σ2) x
- 7. Параллельность двух плоскостей Признак параллельности: плоскости параллельны,
- 8. Параллельность двух плоскостей Искомая плоскость Θ задается
- 9. Σ Пересечение прямой с проецирующей плоскостью
- 10. Пересечение плоскости общего положения с проецирующей
- 11. Пересечение плоскости общего положения с проецирующей
- 12. Пересечение прямой общего положения с
- 13. 1 ПО. Пересечение прямой общего
- 14. 1 ПО. Пересечение прямой общего
- 15. 1 ПО. Пересечение прямой общего
Слайд 2Взаимное положение прямой и плоскости, двух плоскостей
Прямая принадлежит плоскости (см. тема
Прямая параллельна плоскости: общих точек нет
Прямая пересекает плоскость: одна общая точка
Плоскости параллельны: общих прямых нет
Плоскости пересекаются: одна общая прямая
Прямая и плоскость:
Две плоскости:
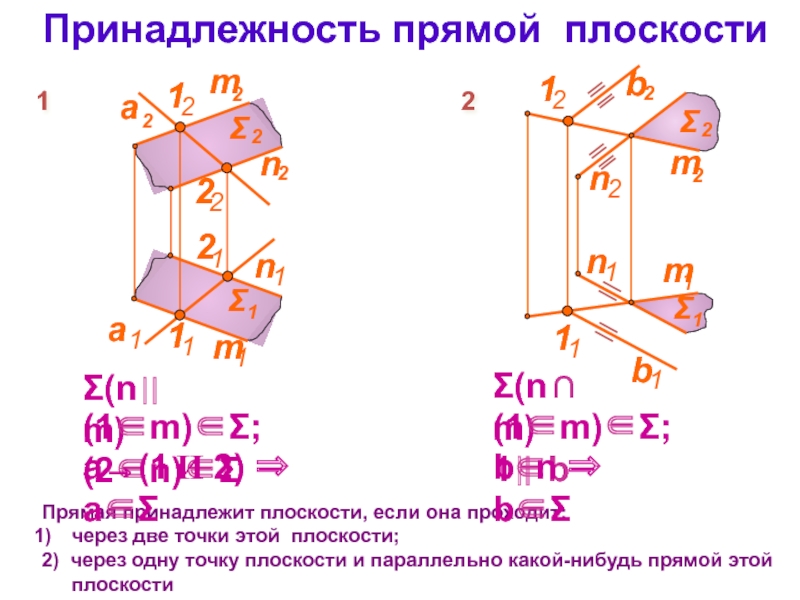
Слайд 3Принадлежность прямой плоскости
Прямая принадлежит плоскости, если она проходит:
через две точки
2) через одну точку плоскости и параллельно какой-нибудь прямой этой плоскости
Σ(n⎟⎟ m)
1
(1∈m)∈Σ; (2∈n)∈Σ
а→(1 И 2) ⇒ а∈Σ
2
Σ(n ∩ m)
(1∈m)∈Σ; 1∈b
b⎟⎟ n ⇒ b∈Σ
Слайд 4
Параллельность прямой и плоскости
Через точку А в пространстве можно провести бесчисленное
Σ
b
Прямая параллельна
плоскости, если она
параллельна какой-либо
прямой, лежащей в
этой плоскости
А
Признак параллельности:
b⎟⎟ n∈Σ ⇒ b⎟⎟ Σ
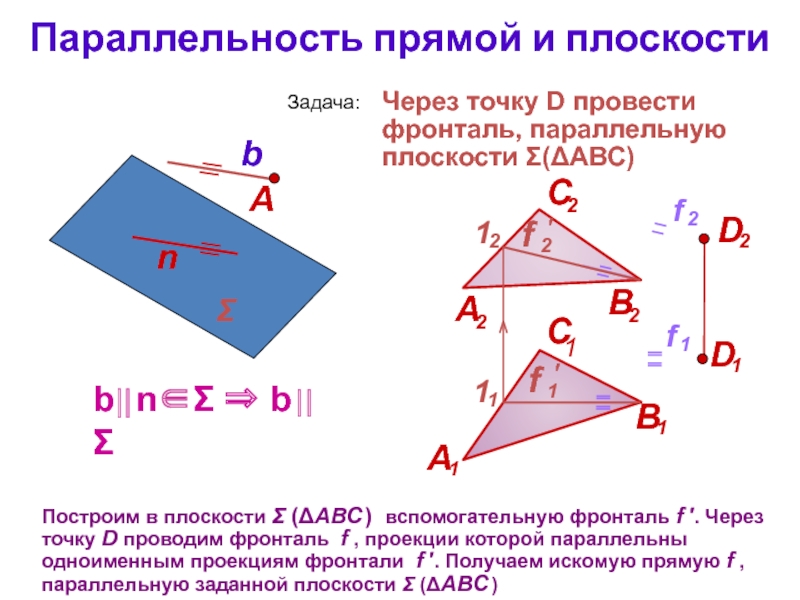
Слайд 5Параллельность прямой и плоскости
Построим в плоскости Σ (ΔАВС ) вспомогательную фронталь
Σ
b
Через точку D провести фронталь, параллельную плоскости Σ(ΔАВС)
Задача:
b⎟⎟ n∈Σ ⇒ b⎟⎟ Σ
А
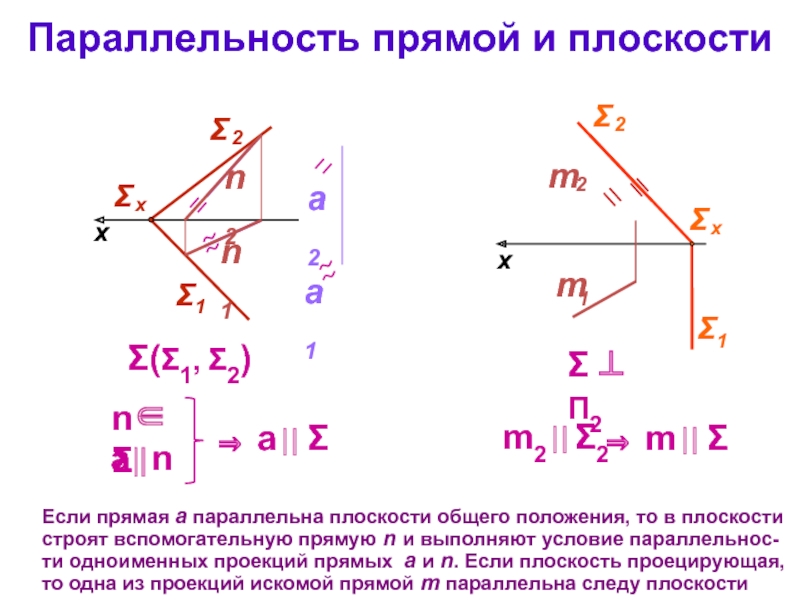
Слайд 6Параллельность прямой и плоскости
Σ(Σ1, Σ2)
x
Если прямая а параллельна плоскости общего положения,
n1
n2
а2
а⎟⎟ n
x
Σ ⊥ П2
n∈Σ
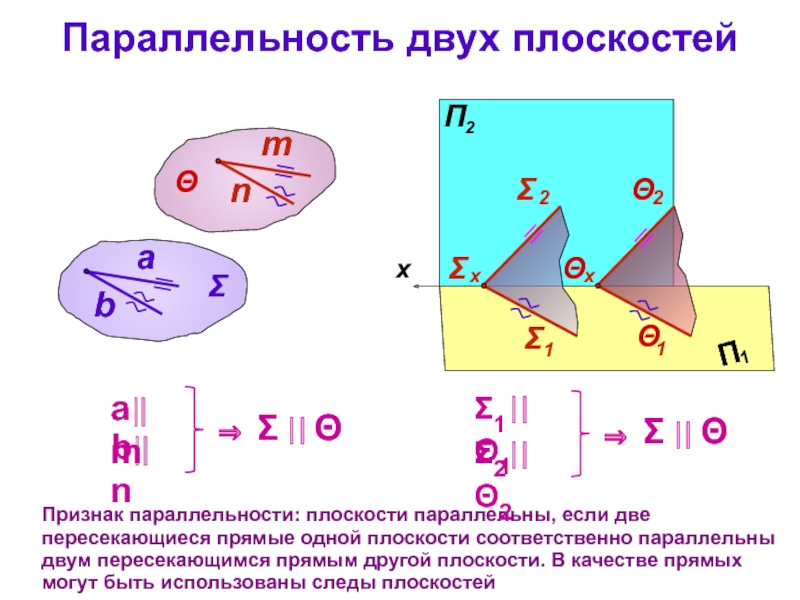
Слайд 7Параллельность двух плоскостей
Признак параллельности: плоскости параллельны, если две пересекающиеся прямые одной
b⎟⎟ n
а⎟⎟ m
Σ1⎟⎟ Θ1
Σ2⎟⎟ Θ2
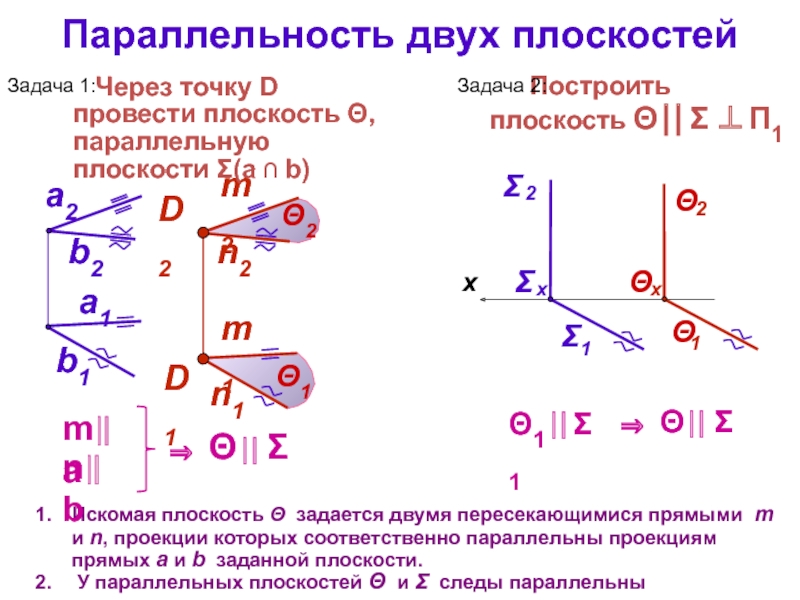
Слайд 8Параллельность двух плоскостей
Искомая плоскость Θ задается двумя пересекающимися прямыми m и
У параллельных плоскостей Θ и Σ следы параллельны
n⎟⎟ b
b1
a1
m⎟⎟ a
Θ1⎟⎟ Σ 1
⇒ Θ⎟⎟ Σ
b2
a2
Через точку D провести плоскость Θ, параллельную плоскости Σ(a ∩ b)
Задача 1:
Слайд 9
Σ
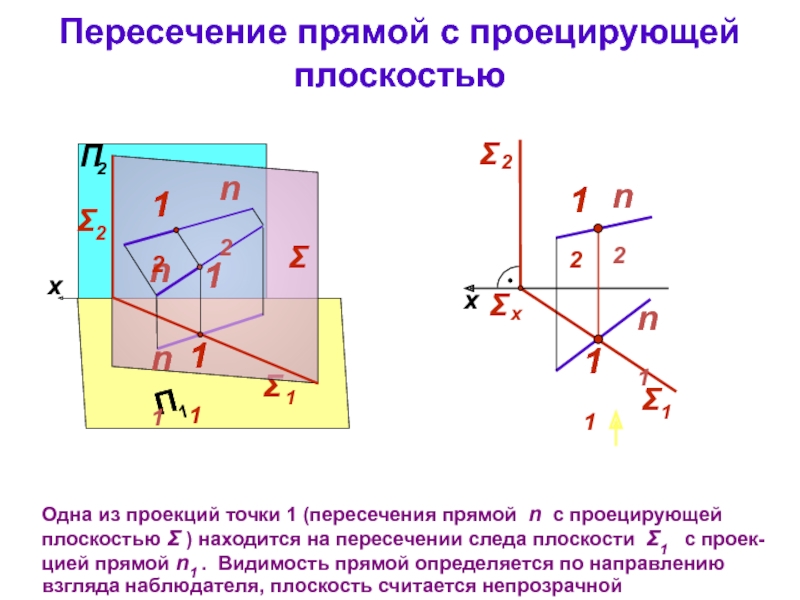
Пересечение прямой с проецирующей плоскостью
Одна из проекций точки 1 (пересечения прямой
n2
Слайд 10Пересечение плоскости общего
положения с проецирующей плоскостью
Две плоскости пересекаются по прямой
– горизонтально
проецирующая плоскость;
Θ(Δ) – плоскость
общего положения
Θ
Θ1
Θ2
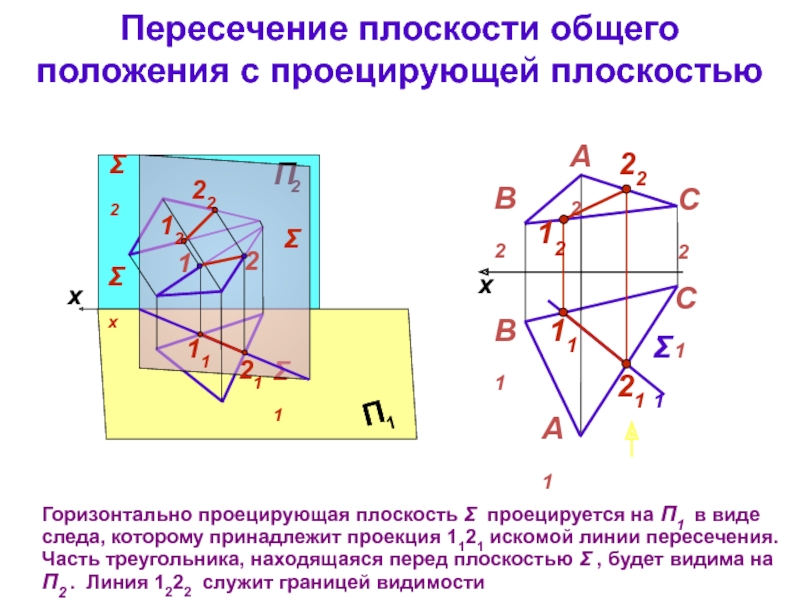
Слайд 11Пересечение плоскости общего
положения с проецирующей плоскостью
Горизонтально проецирующая плоскость Σ проецируется
Слайд 12
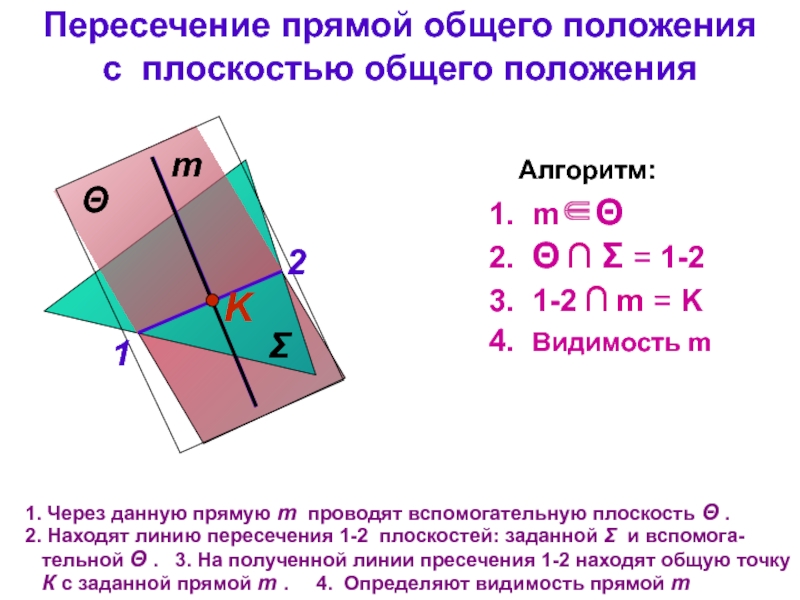
Пересечение прямой общего положения
с плоскостью общего положения
Σ
m
Через данную прямую
Находят линию пересечения 1-2 плоскостей: заданной Σ и вспомога-тельной Θ . 3. На полученной линии пресечения 1-2 находят общую точку К с заданной прямой m . 4. Определяют видимость прямой m
Алгоритм:
1. m∈Θ
2. Θ ∩ Σ = 1-2
3. 1-2 ∩ m = K
4. Видимость m
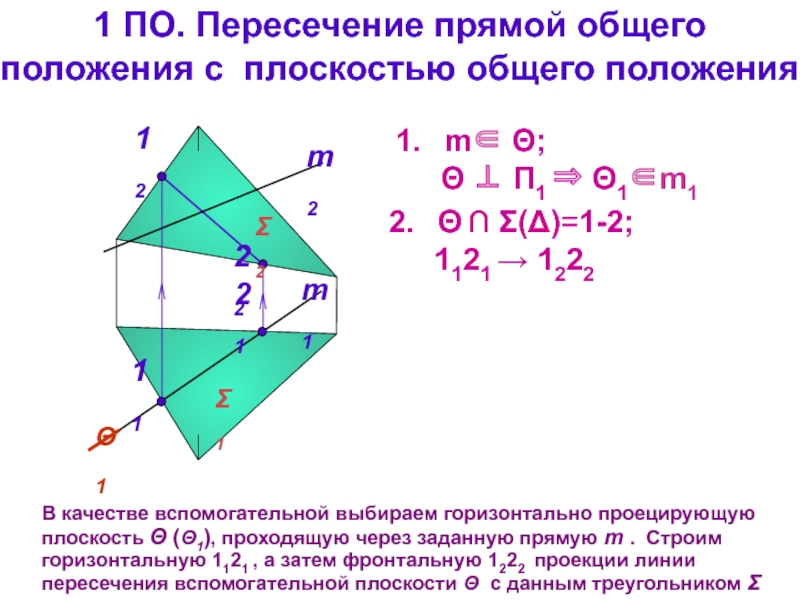
Слайд 13
1 ПО. Пересечение прямой общего
положения с плоскостью общего положения
m1
m2
В качестве
m∈ Θ;
Θ ⊥ П1 ⇒ Θ1∈m1
Θ ∩ Σ(Δ)=1-2;
1121 → 1222
Σ1
Σ2
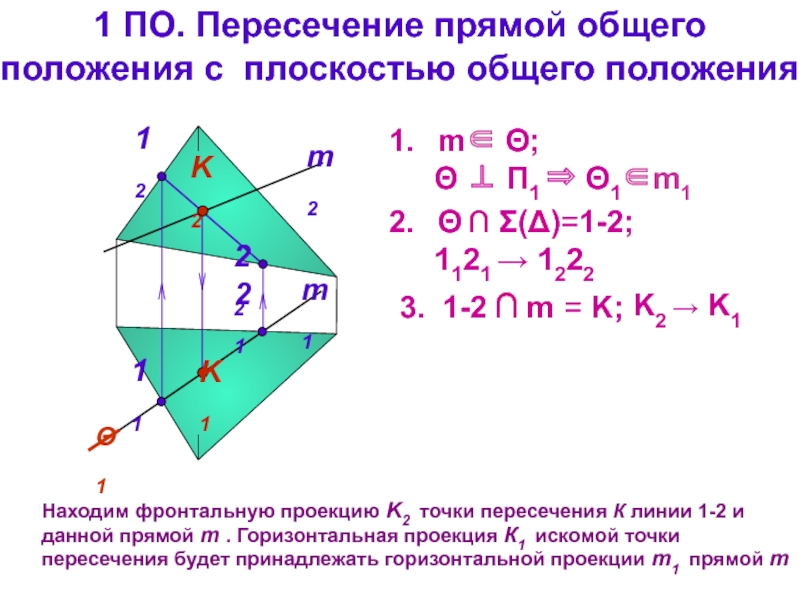
Слайд 14
1 ПО. Пересечение прямой общего
положения с плоскостью общего положения
m1
m2
Находим фронтальную
m∈ Θ;
Θ ⊥ П1 ⇒ Θ1∈m1
Θ ∩ Σ(Δ)=1-2;
1121 → 1222
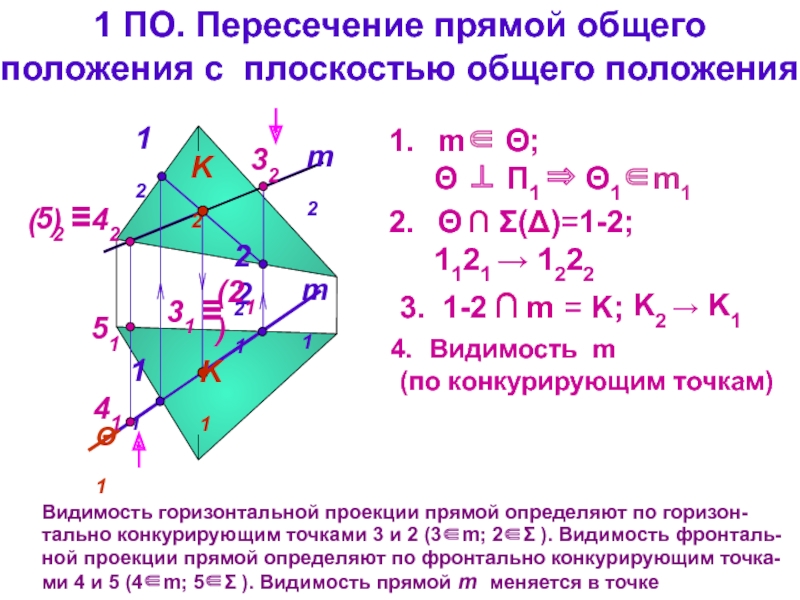
Слайд 15
1 ПО. Пересечение прямой общего
положения с плоскостью общего положения
m1
m2
Видимость горизонтальной
21
Видимость m
(по конкурирующим точкам)
(21)
( )
m∈ Θ;
Θ ⊥ П1 ⇒ Θ1∈m1
Θ ∩ Σ(Δ)=1-2;
1121 → 1222