- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Возрастание и убывание функций презентация
Содержание
- 1. Возрастание и убывание функций
- 2. Если производная дифференцируемой функции положительна внутри
- 3. ДОКАЗАТЕЛЬСТВО: Рассмотрим значения х1 и х2, принадлежащие
- 4. и правая часть последнего равенства тоже будет
- 5. ТЕОРЕМА 2. (достаточное условие убывания
- 6. Геометрическая интерпретация Если касательные к кривой
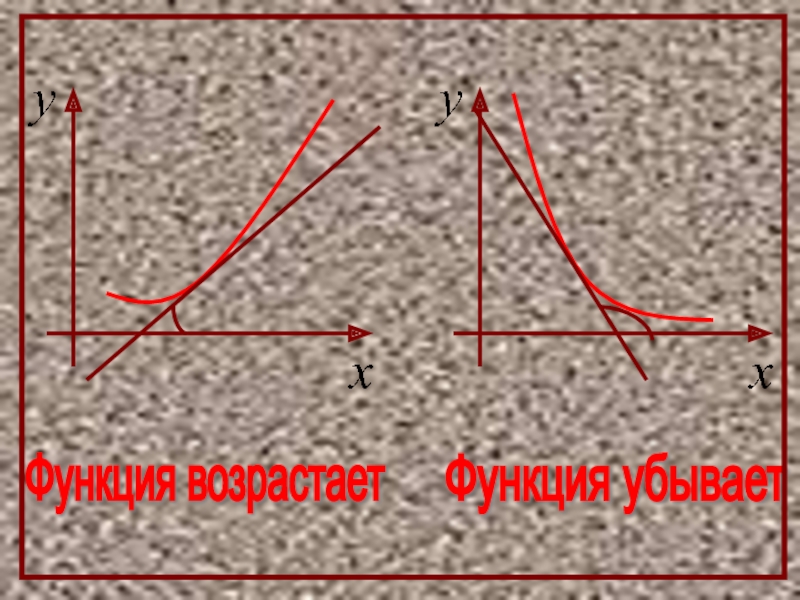
- 7. Функция возрастает Функция убывает
- 8. Пример. Найти интервалы монотонности функции
- 9. Решение: Найдем производную этой функции: Исследуем
Если производная дифференцируемой функции положительна внутри некоторого промежутка Х, то функция возрастает на этом промежутке.
Слайд 2Если производная дифференцируемой
функции положительна внутри
некоторого промежутка Х, то функция
возрастает на
этом промежутке.
Слайд 3ДОКАЗАТЕЛЬСТВО:
Рассмотрим значения х1 и х2, принадлежащие промежутку Х.
Пусть
Для функции f(x) на
отрезке [x1;x2] выполняется теорема Лагранжа:
где
Т.е. ξ принадлежит промежутку, на котором производная функции положительна:
Слайд 4и правая часть последнего равенства тоже будет положительна:
Тогда левая часть
тоже будет положительна:
То есть
Получили, что большему значению аргумента соответствует большее значение функции.
Это означает, что функция возрастает.
Слайд 5ТЕОРЕМА 2.
(достаточное условие
убывания функции)
Если производная дифференцируемой
функции отрицательна внутри
некоторого
промежутка Х, то она
убывает на этом промежутке.
убывает на этом промежутке.
Слайд 6Геометрическая
интерпретация
Если касательные к кривой на некотором
промежутке направлены под острыми
углами
к оси х, то функция возрастает.
если они направлены под тупыми углами,
то функция убывает.
если они направлены под тупыми углами,
то функция убывает.
Слайд 9Решение:
Найдем производную этой функции:
Исследуем знак этой производной:
Следовательно, функция будет
возрастать на промежутке
Функция будет убывать на промежутке
