- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Визначник другого та третього порядків. Алгебраїчні доповнення презентация
Содержание
- 1. Визначник другого та третього порядків. Алгебраїчні доповнення
- 2. План Визначники Мінори Алгебраїчні доповнення
- 3. Визначники До квадратної матриці А
- 5. На відміну від матриці визначник обмежується справа та зліва одинарною лінією.
- 6. Щоб знайти визначник другого порядку, множимо
- 7. Приклад:
- 8. При обчисленні визначника 3-го порядку зручно користуватися
- 9. Приклад:
- 10. Мінори Означення. Мінором Мij, що відповідає
- 11. Алгебраїчні доповнення Означення. Алгебраїчним доповненням Аij,
- 12. Приклад: Дано матрицю Обчислити
- 13. Алгебраїчні доповнення: теореми. Теорема 1. (Теорема Лапласа)
- 14. Приклад: Обчислити визначник розкладаючи його за елементами третього рядка:
- 15. Теорема 2. Сума добутків елементів будь-якого
- 16. Запитання для самоконтролю 1. Що називається
Слайд 3Визначники
До квадратної матриці А порядку n можно зіставити число
detA ( ), яке називається її визначником (детермінантом) наступним чином:
Слайд 6
Щоб знайти визначник другого порядку,
множимо елементи головної діагоналі та
віднімаємо добуток елементів
побічної
діагоналі:
Обчислення визначника другого порядку ілюструється схемою:
діагоналі:
Обчислення визначника другого порядку ілюструється схемою:
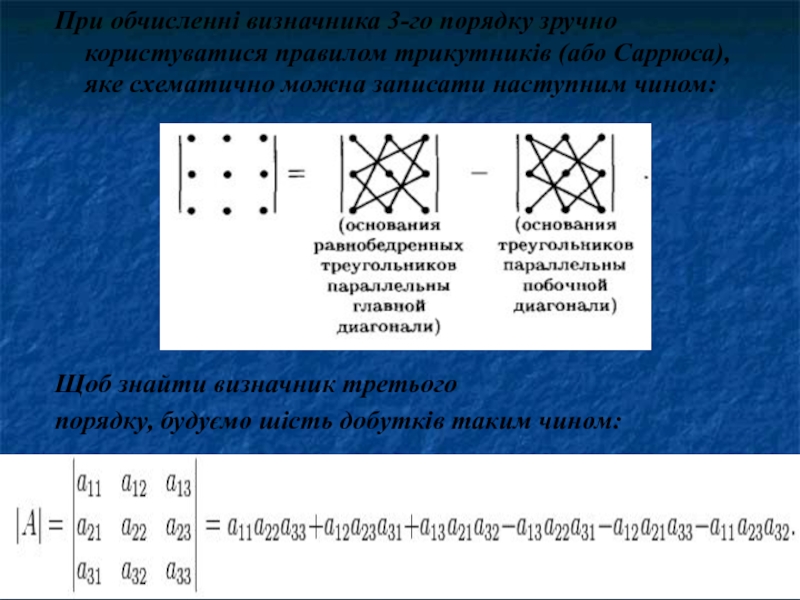
Слайд 8При обчисленні визначника 3-го порядку зручно користуватися правилом трикутників (або Саррюса),
яке схематично можна записати наступним чином:
Щоб знайти визначник третього
порядку, будуємо шість добутків таким чином:
Щоб знайти визначник третього
порядку, будуємо шість добутків таким чином:
Слайд 10Мінори
Означення.
Мінором Мij, що відповідає елементу аij
матриці, називається визначник, який
відповідає матриці, утвореній з матриці
викреслюванням i-го рядка та j-го стовпця.
Слайд 11Алгебраїчні доповнення
Означення. Алгебраїчним доповненням Аij,
що відповідає елементу аij матриці,
називається
відповідний мінор, взятий зі
знаком “+”, якщо сума його індексів парна, і
зі знаком “-”, якщо сума його індексів
непарна.
знаком “+”, якщо сума його індексів парна, і
зі знаком “-”, якщо сума його індексів
непарна.
Слайд 13Алгебраїчні доповнення: теореми.
Теорема 1. (Теорема Лапласа)
Значення визначника п-го порядку, що
визначає матрицю, дорівнює сумі добутків
елементів довільного рядка або довільного стовпця
на відповідні алгебраїчні доповнення.
Для визначника виконуються такі
рівності:
Слайд 15Теорема 2. Сума добутків елементів будь-якого
рядка або стовпця визначника на
алгебраїчні
доповнення відповідних елементів іншого рядка,
чи стовпця дорівнюють нулю.
доповнення відповідних елементів іншого рядка,
чи стовпця дорівнюють нулю.
Слайд 16Запитання для самоконтролю
1. Що називається визначником n-го порядку?
2. Що називається мінором
та алгебраїчним доповненням елементу визначника ?
3. Які способи обчислення визначників ?
4. Які операції над визначниками не змінюють їх?
3. Які способи обчислення визначників ?
4. Які операції над визначниками не змінюють їх?