- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Векторы в пространстве презентация
Содержание
- 1. Векторы в пространстве
- 2. Понятие вектора Отрезок, для которого указано, какая
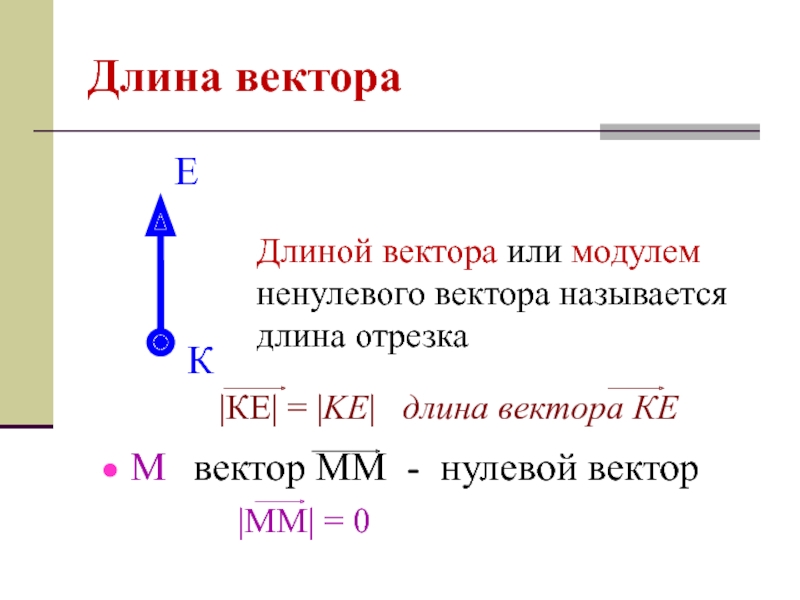
- 3. Длина вектора Длиной вектора или модулем ненулевого вектора называется длина отрезка
- 4. Нулевой вектор считается коллинеарным любому вектору Коллинеарные
- 5. Сонаправленные векторы Коллинеарные векторы, имеющие одинаковое направление, называются сонаправленными векторами
- 6. Противоположно направленные векторы Коллинеарные векторы, имеющие противоположное направление, называются противоположно направленными векторами
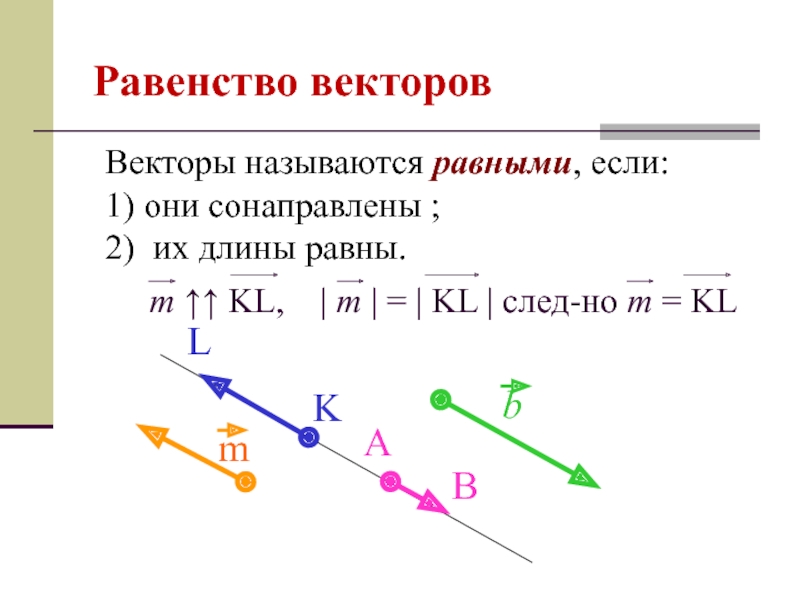
- 7. Равенство векторов Векторы называются равными, если:
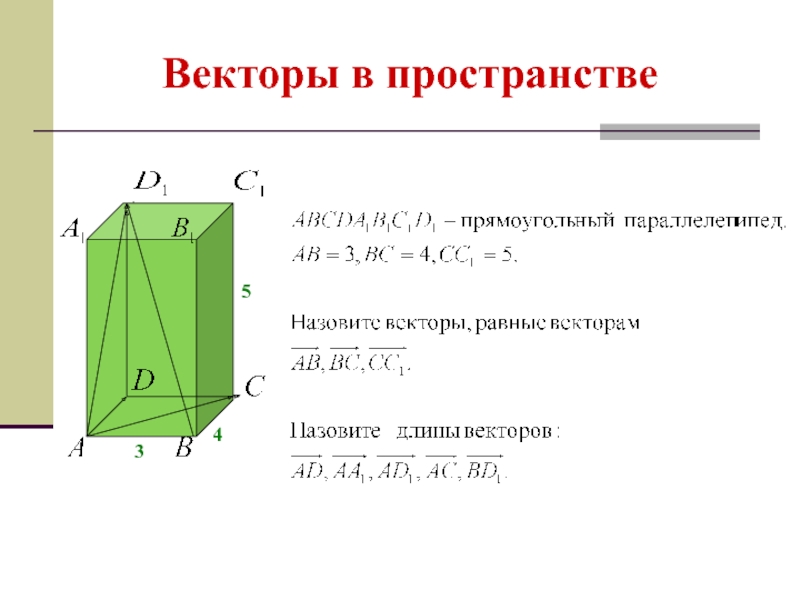
- 8. Векторы в пространстве
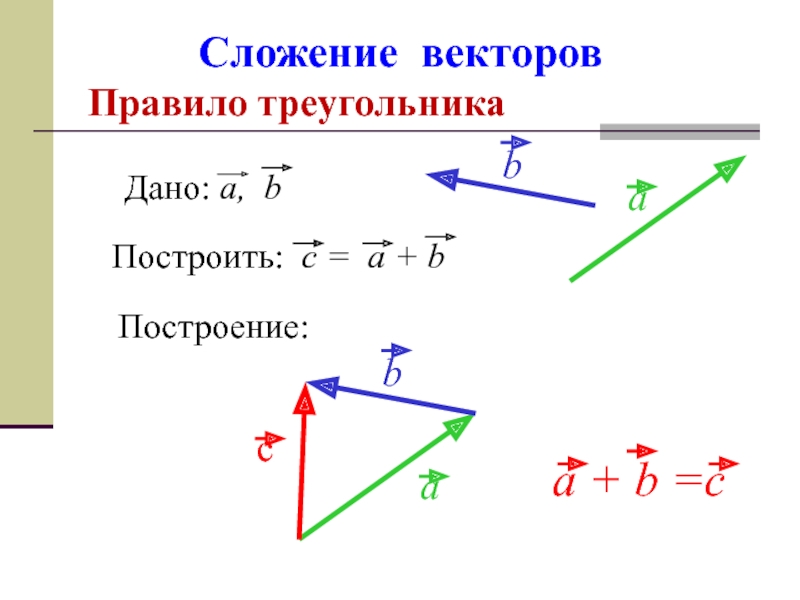
- 9. Сложение векторов Правило треугольника Построение:
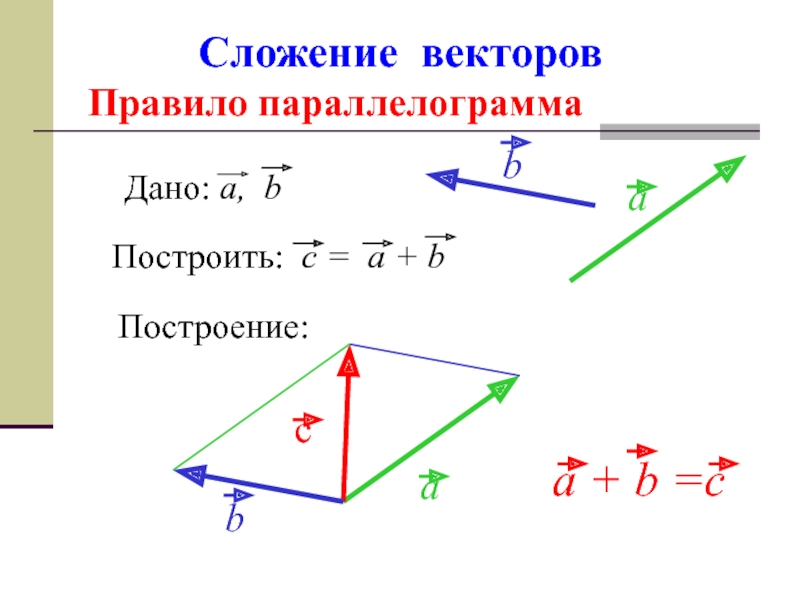
- 10. Сложение векторов Правило параллелограмма Построение:
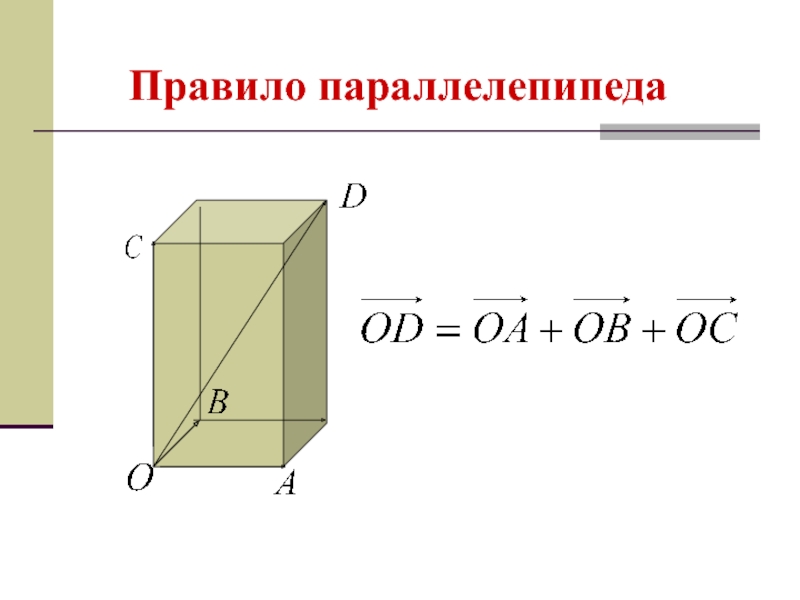
- 11. Правило параллелепипеда
- 12. Правило многоугольника
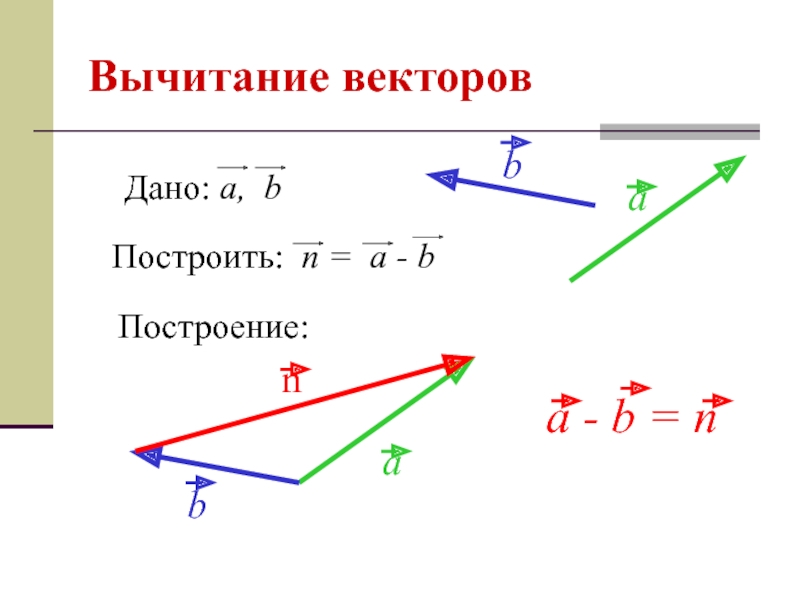
- 13. Вычитание векторов Построение:
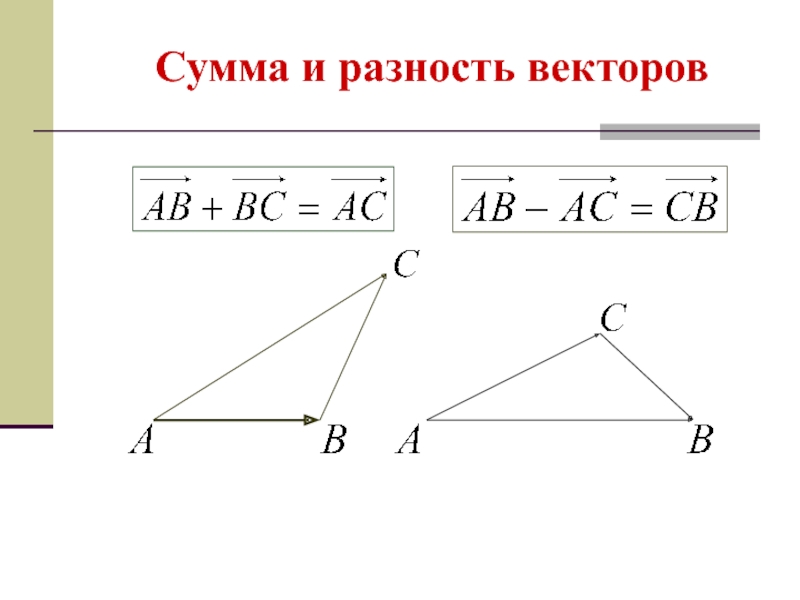
- 14. Сумма и разность векторов
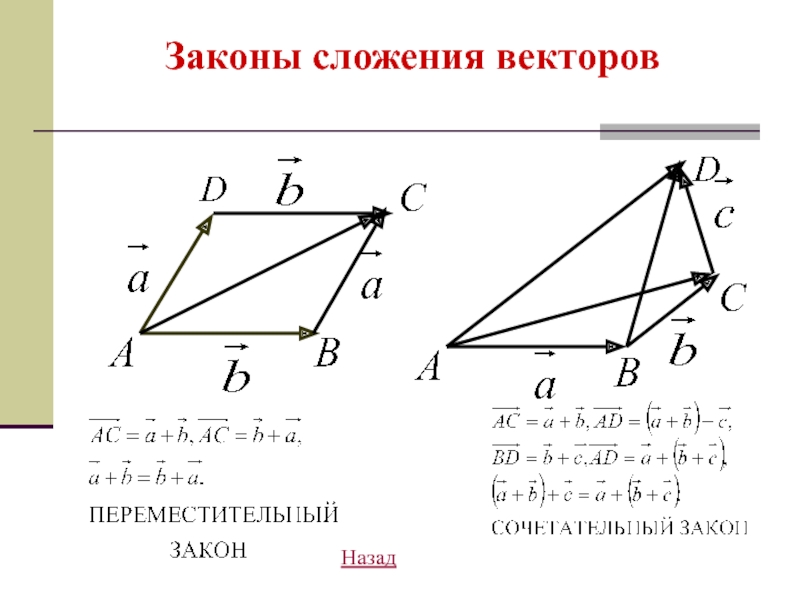
- 15. Законы сложения векторов Назад
- 16. Умножение вектора a на число k k·a
- 17. Умножение вектора на число
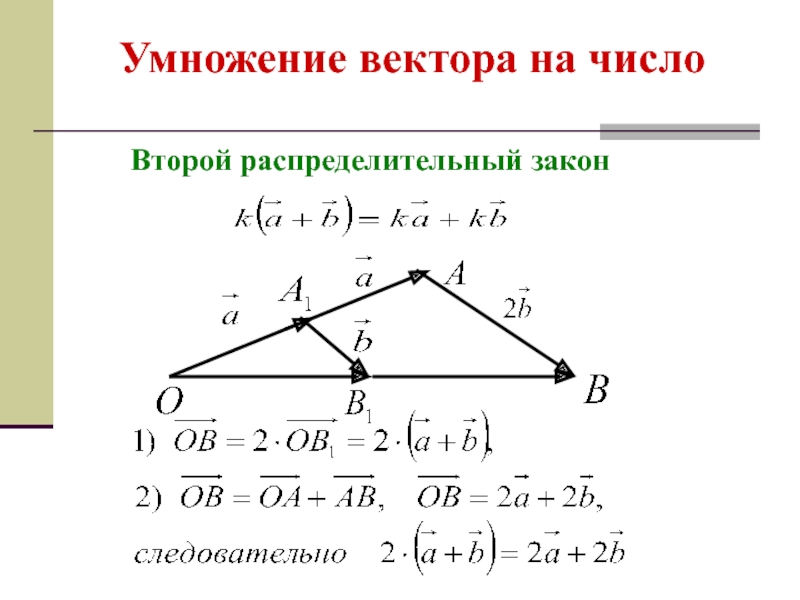
- 18. Умножение вектора на число
- 19. Умножение вектора на число
- 20. Компланарные векторы Векторы называются компланарными, если
- 21. Компланарные векторы
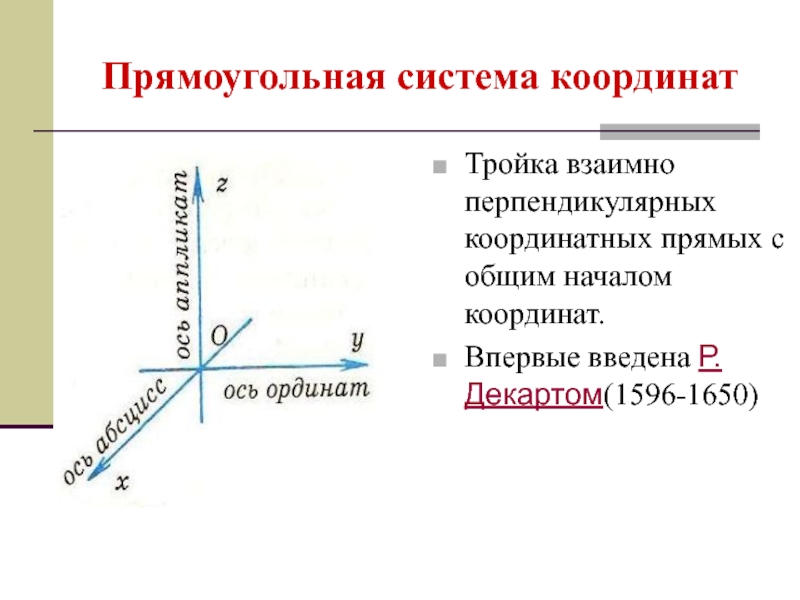
- 22. Прямоугольная система координат Тройка взаимно перпендикулярных
- 23. Координаты точки Каждая точка в пространстве
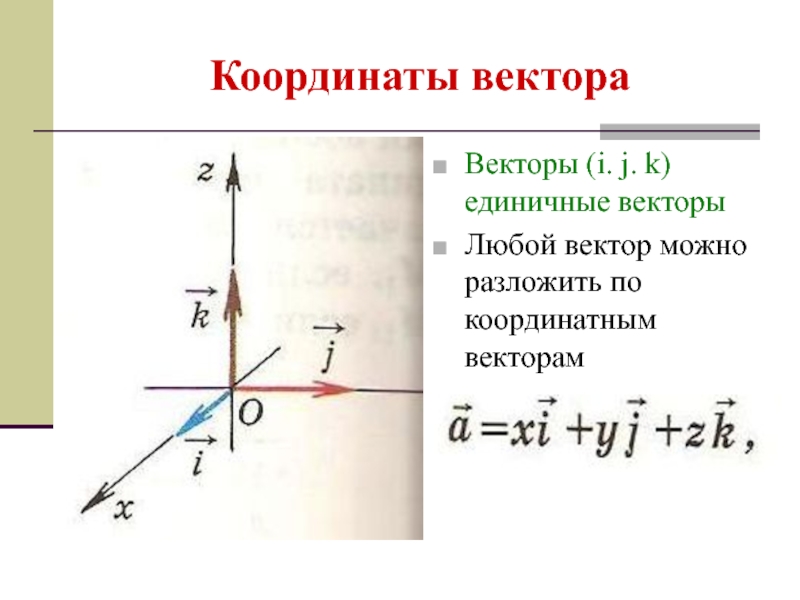
- 24. Координаты вектора Векторы (i. j. k)
- 25. Длина вектора
- 26. Скалярное произведение векторов
- 27. Свойства скалярного произведения. Угол между векторами.
Понятие вектора Отрезок, для которого указано, какая его граничная точка является началом, а какая - концом, называется направленным отрезком или вектором Конец вектора Начало вектора либо а a
Слайд 2Понятие вектора
Отрезок, для которого указано, какая его граничная точка является началом,
а какая - концом, называется направленным отрезком или вектором
Конец вектора
Начало вектора
либо а
a
Слайд 4Нулевой вектор считается коллинеарным любому вектору
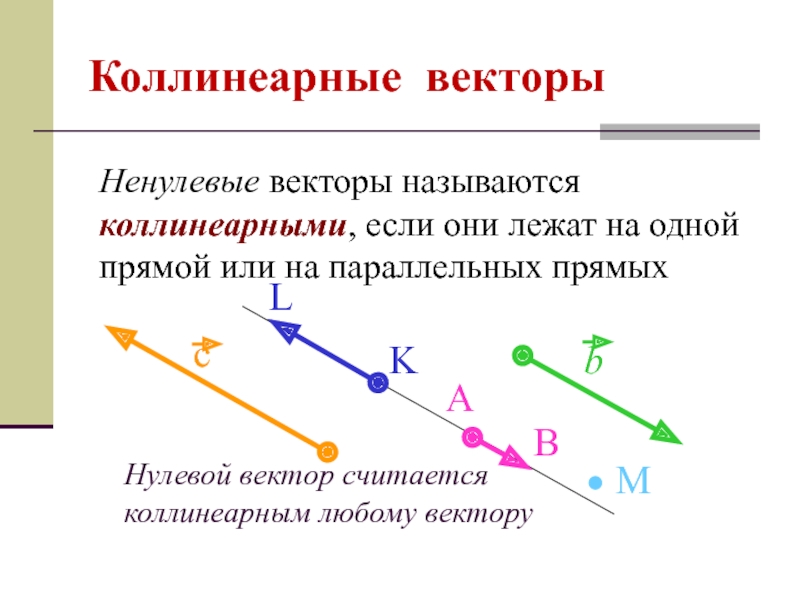
Коллинеарные векторы
Ненулевые векторы называются коллинеарными, если
они лежат на одной прямой или на параллельных прямых
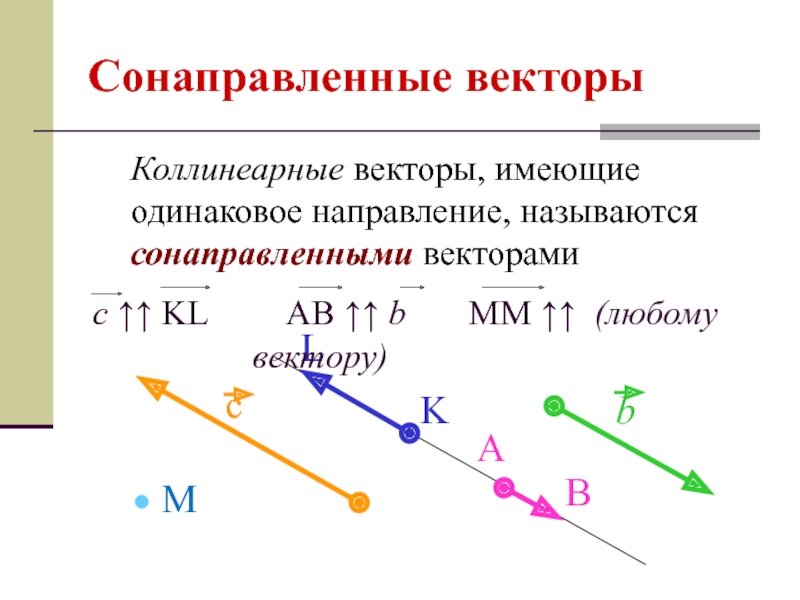
Слайд 5Сонаправленные векторы
Коллинеарные векторы, имеющие одинаковое направление, называются сонаправленными векторами
Слайд 6Противоположно направленные векторы
Коллинеарные векторы, имеющие противоположное направление, называются противоположно направленными векторами
Слайд 16Умножение вектора a на число k
k·a = b,
|a| ≠ 0, k
– произвольное число
|b| = |k|·|a|,
если k> 0, то a ↑↑ b
если k< 0, то a ↑↓ b
|b| = |k|·|a|,
если k> 0, то a ↑↑ b
если k< 0, то a ↑↓ b
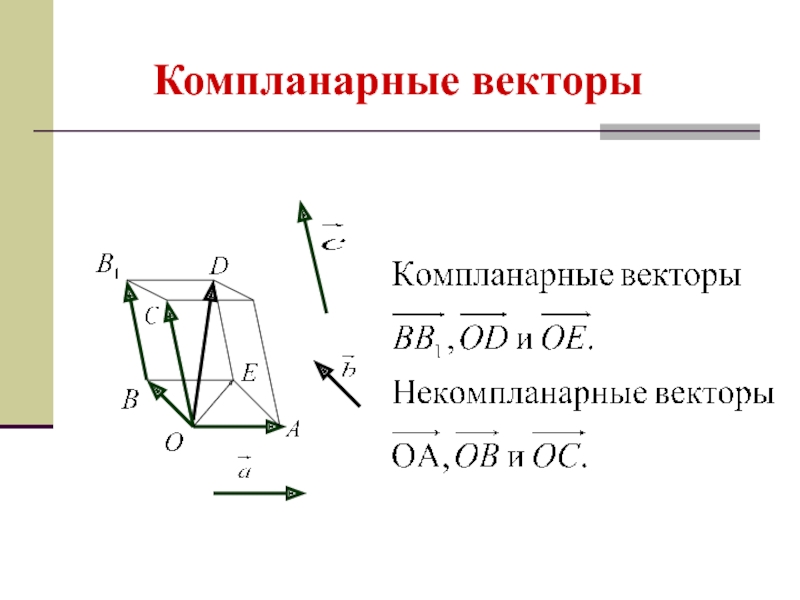
Слайд 20Компланарные векторы
Векторы называются компланарными,
если при откладывании их от одной точки
они будут
лежать в одной плоскости.
лежать в одной плоскости.
Если хотя бы один из трёх векторов — нулевой, то три вектора считаются компланарными.
Тройка векторов, содержащая пару коллинеарных векторов, компланарна.
Замечания
Слайд 22Прямоугольная система координат
Тройка взаимно перпендикулярных координатных прямых с общим началом координат.
Впервые
введена Р.Декартом(1596-1650)
Слайд 23Координаты точки
Каждая точка в пространстве задаётся тройкой чисел (x,y,z ) называемых
координатами точки в пространстве
Слайд 24Координаты вектора
Векторы (i. j. k) единичные векторы
Любой вектор можно разложить по
координатным векторам
