- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Правильні многогранники презентация
Содержание
- 1. Правильні многогранники
- 3. Означення: Опуклий многогранник називається правильним, якщо
- 4. Види правильних опуклих многогранників (Платонові тіла)
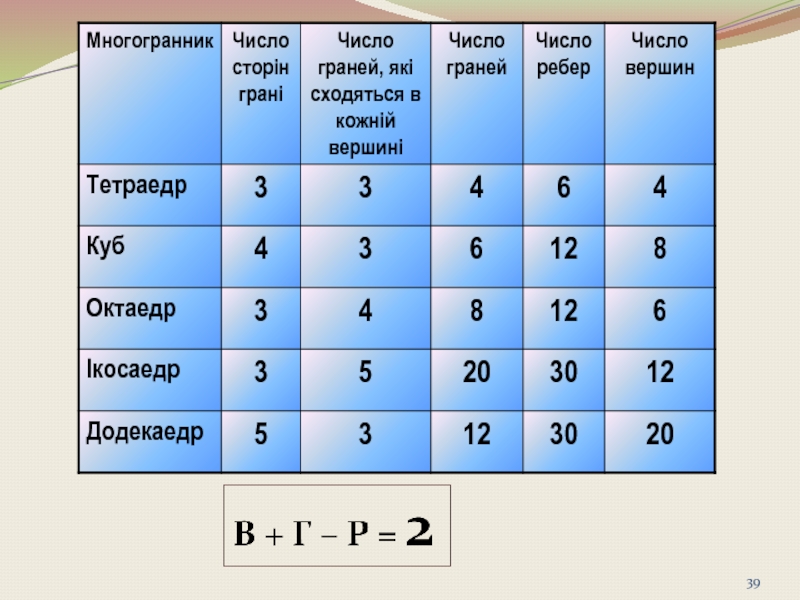
- 5. ● правильний ікосаедр. Існує п’ять типів правильних опуклих
- 6. Назви многогранників прийшли з Давньої Греції,
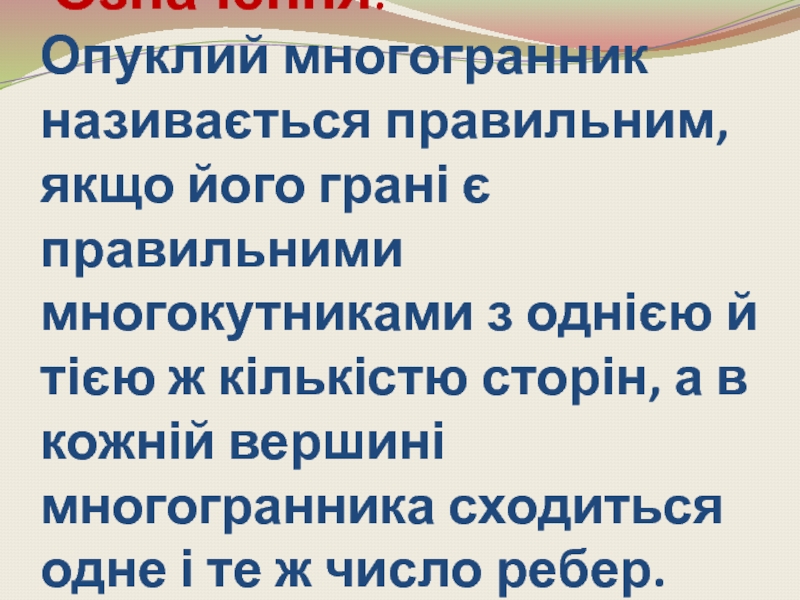
- 8. Тетраедр
- 10. Тетраедр в природі Кристали білого фосфору Будова решітки кристалу алмаза Кристалічна решітка метану
- 11. «Геометрія галактик». Всесвіт влаштований на основі єдиного
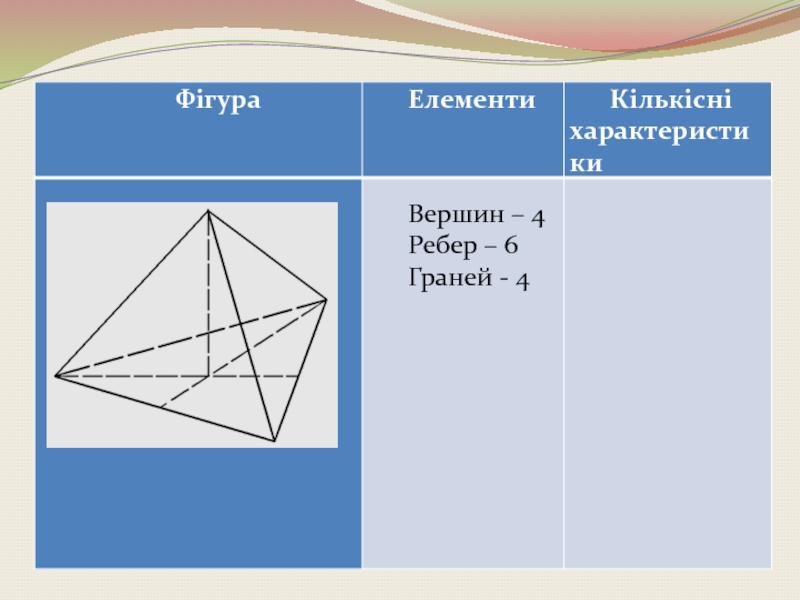
- 12. Гексаедр Куб (гексаедр) Складений з шести квадратів.
- 14. Куб в природі Кристалічна решітка повареної солі Форму куба мають кристалічні решітки багатьох металів
- 15. «Дірявий» куб в Ноттердамі»
- 16. Парафіяльна церква Серця Христа
- 17. Кааба в Мецці
- 18. «Куб» у центрі Німеччини.
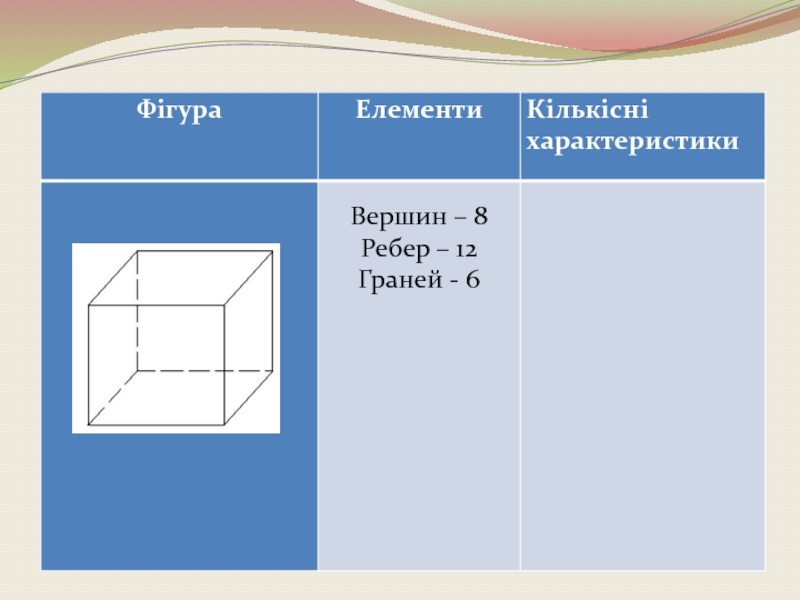
- 19. Октаедр Правильний октаедр складений з восьми
- 21. Октаедр в природі Вуглець С характеризується структурою октаедра Кристали алмазу
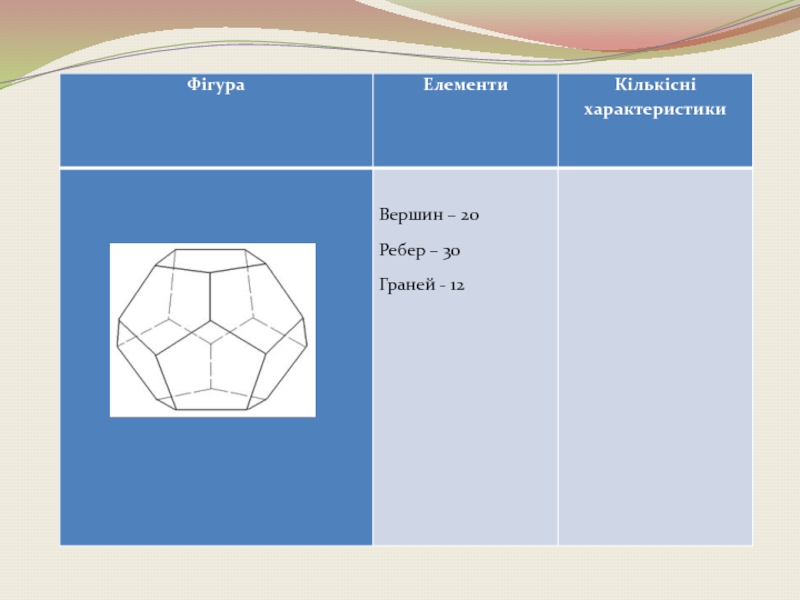
- 22. Додекаедр Правильний додекаедр складений з дванадцяти правильних
- 24. Додекаедр в природі Вірус поліомієліту Молекула ДНК складається з взаємовідносин ікосаедрів та додекаедрів
- 25. «У променях кристала Землі»
- 26. Ікосаедр Правильний ікосаедр складений з двадцяти рівносторонніх
- 28. Ікосаедр в природі Кристал бору має форму ікосаедра
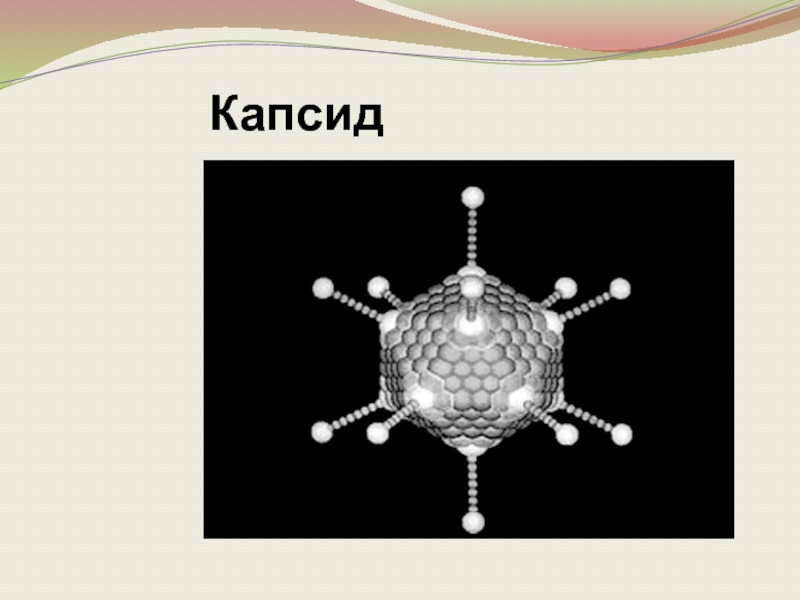
- 29. Ікосаедр в природі Капсиди багатьох вірусів (наприклад бактеріофаги, мімівірус)
- 30. У біології німецький біолог Еге Геккель
- 31. Капсид
- 32. Легко впевнитись, що вершини кожного з п’яти
- 33. Правильні многогранникив філософській картині світу Платона
- 34. Платонові тіла
- 35. Пікассо «Дівчинка на кулі»
- 36. Правильні многогранники і мистецтво Сальвадор Далі «Тайна вечеря»
- 37. Моріц Ешер «Зірка»
- 38. Число вершин плюс число граней мінус
- 40. Тіла Архімеда Крім правильних многогранників
- 41. 4 трикутники 4 шестикутники Зрізаний тетраедр
- 42. Тіла Пуансона Малий зірковий додекаедр
Слайд 2 Епіграф. Правильних многогранників надзвичайно мало, але цей дуже скромний за кількістю
Слайд 3 Означення: Опуклий многогранник називається правильним, якщо його грані є правильними многокутниками
Слайд 5● правильний ікосаедр.
Існує п’ять типів правильних опуклих многогранників:
● правильний тетраедр;
● правильний гексаедр (куб);
● правильний октаедр;
● правильний
Слайд 6 Назви многогранників
прийшли з Давньої Греції, в них вказано кількість граней:
«едра» − грань;
«тетра» − 4;
«гекса» − 6;
«окта» − 8;
«ікоса» − 20;
«додека» − 12.
Слайд 10Тетраедр в природі
Кристали білого фосфору
Будова решітки кристалу алмаза
Кристалічна решітка метану
Слайд 11«Геометрія галактик».
Всесвіт влаштований на основі єдиного геометричного принципу (по І.Кеплеру).
У
У сферу Юпітера вписуємо тетраедр, в тетраедр –сферу Марса.
У сферу Марса вписуємо додекаедр, в додекаедр – сферу Землі.
У сферу Землі вписуємо ікосаедр, в ікосаедр – сферу Венери.
У сферу Венери вписуємо октаедр, в октаедр – сферу Меркурія..
У центр всієї системи І.Кеплер помістив Сонце.
Слайд 12Гексаедр
Куб (гексаедр) Складений з шести квадратів. Кожна вершина куба є вершиною
Слайд 14Куб в природі
Кристалічна решітка повареної солі
Форму куба мають кристалічні решітки багатьох
Слайд 19 Октаедр
Правильний октаедр складений з восьми рівносторонніх трикутників. Кожна вершина октаедра
Слайд 22Додекаедр
Правильний додекаедр складений з дванадцяти правильних пятикутників. Кожна вершина додекаедра є
Слайд 24Додекаедр в природі
Вірус поліомієліту
Молекула ДНК складається з взаємовідносин ікосаедрів та додекаедрів
Слайд 26Ікосаедр
Правильний ікосаедр складений з двадцяти рівносторонніх трикутників. Кожна вершина ікосаедра є
Слайд 30У біології німецький біолог Еге Геккель
початку ХХ століття дослідив,що одноклітинні
організми
передають форму ікосаедра
Слайд 32Легко впевнитись, що вершини кожного з п’яти видів правильних многогранників, в
На поверхні сферичної основи встановили 12 точок, рівномірно розділених по каркасу (вершини ікосаедра). Машина намотує нейлонові нитки по колам великих кругів, які проходять через кожну пару зазначених точок. Коли таке намотування буде повторено багато разів, причому, починаючи щоразу з різних пар точок, камера буде покрита цілком рівномірно, що забезпечить однакову міцність кожного її квадратного сантиметра.
Слайд 33 Правильні многогранникив філософській картині світу Платона Правильні многогранники іноді називають
Платон (≈ 428 – 348 до н.е.)
Вони займали визначне місце в ідеалістичній картині світу давньогрецького філософа Платона.
Чотири з них відображали чотири «суті» або «стихії»:
тетраедр – вогонь,
ікосаедр – воду,
гексаедр – землю,
октаедр – повітря.
П’ятий многогранник – додекаедр, вважався найголовнішим, втілював в собі «все істотне», символізував все світосприйняття – весь всесвіт.
Слайд 38Число вершин плюс
число граней мінус
число ребер дорівнює два
Теорема Ейлера
В
Леонард Ейлер
(1707 – 1783 рр.)
німецький математик и фізик
Слайд 40Тіла Архімеда
Крім правильних многогранників є напівправильні. Напівправильні многогранники або архимедові
Слайд 414 трикутники
4 шестикутники
Зрізаний тетраедр
Кирпатий додекаедр
80 трикутників
12 п'ятикутників
Зрізаний ікосаедр
12 п'ятикутників
20 шестикутників
Ікосододекаедр
20 трикутників
12 п'ятикутників
Кубооктаедр
8 трикутників
6 квадратів