- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Векторы. Разложение вектора по направлениям. Координаты вектора. Скалярное произведение векторов презентация
Содержание
- 1. Векторы. Разложение вектора по направлениям. Координаты вектора. Скалярное произведение векторов
- 2. Длиной или модулем вектора называется длина отрезка
- 3. Два ненулевых вектора называются колли-неарными, если они
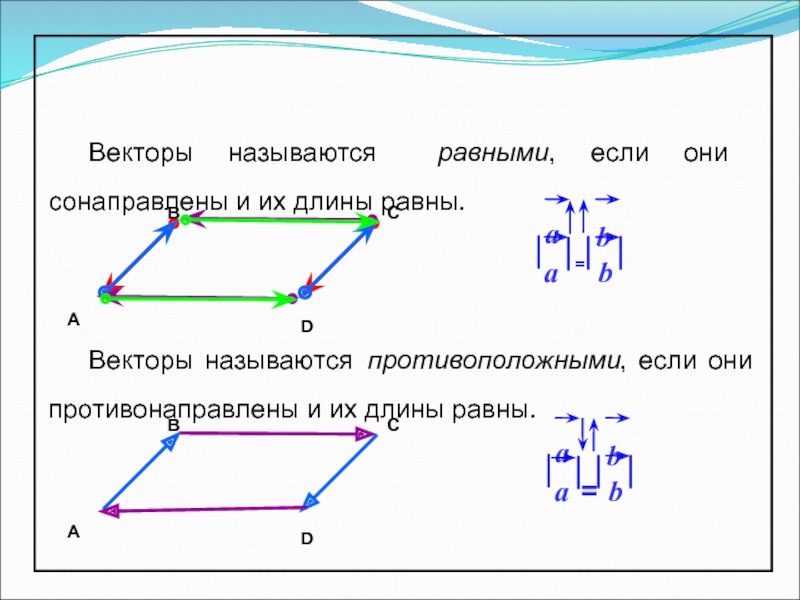
- 4. Векторы называются противоположными, если они противонаправлены и
- 6. Любой вектор можно разложить по координатным векторам,
- 7. Вектор, конец которого совпадает с данной точкой,
- 8. Координаты середины отрезка Длина вектора по его координатам:
- 9. Даны векторы: Найти вектор, равный:
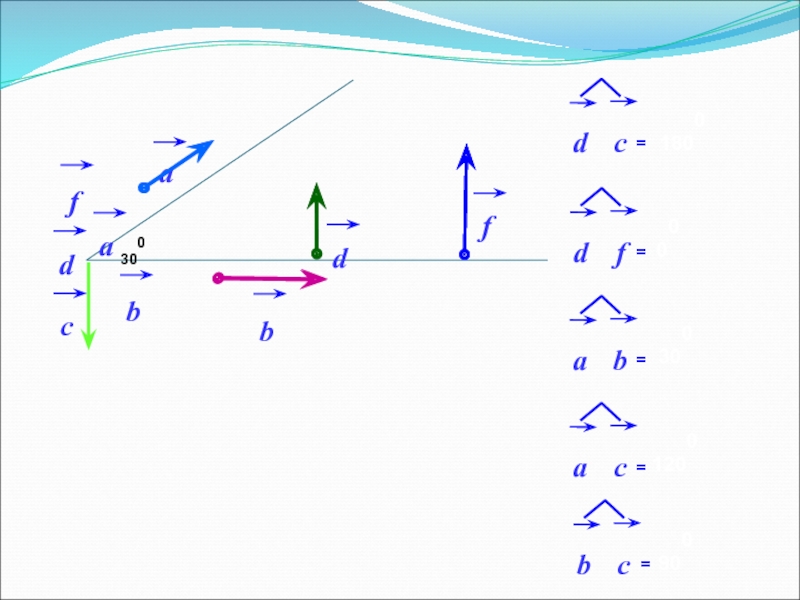
- 10. О А В α Если
- 12. Скалярное произведение векторов – число (скаляр). Скалярным
- 13. Если угол между векторами острый, то скалярное
- 14. Пусть векторы заданы
Слайд 1
Векторы
Разложение вектора по направлениям Координаты вектора
Скалярное произведение векторов
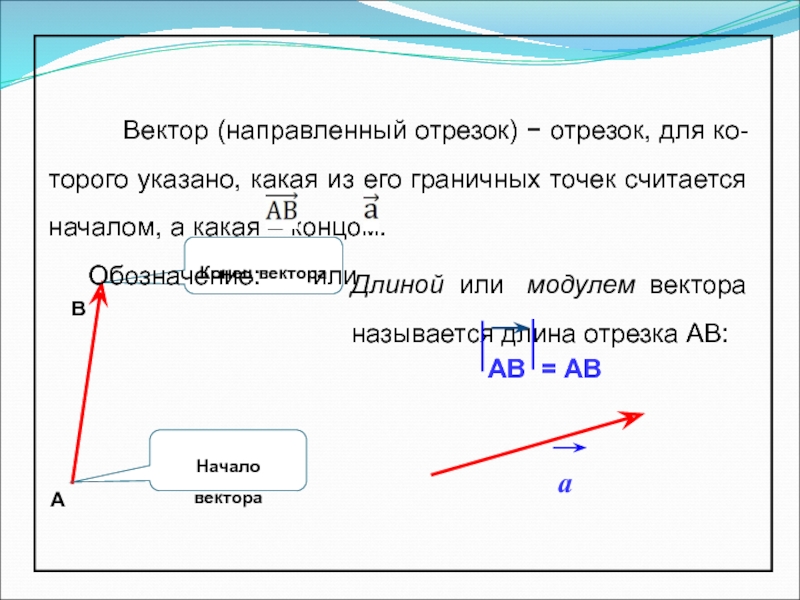
Слайд 2Длиной или модулем вектора называется длина отрезка АВ:
Обозначение: или
Слайд 3Два ненулевых вектора называются колли-неарными, если они лежат на одной прямой
Коллинеарные, сонаправленные векторы
Коллинеарные,
противоположно направленные векторы
Слайд 6Любой вектор можно разложить по координатным векторам, т.е. представить в виде:
Нулевой вектор также можно представить в таком виде:
Координаты равных векторов соответственно равны:
Сумма (разность) векторов:
Произведение вектора на число:
Слайд 7Вектор, конец которого совпадает с данной точкой, а на-чало – с
Слайд 12Скалярное произведение векторов – число (скаляр).
Скалярным произведением двух векторов называется произведение
Если векторы перпендикулярны, то скалярное произведение этих векторов равно нулю.
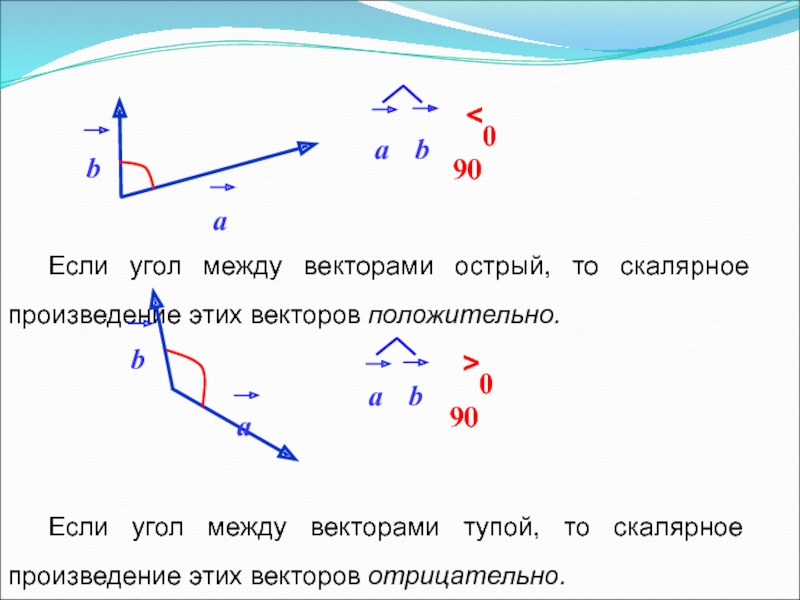
Слайд 13Если угол между векторами острый, то скалярное произведение этих векторов положительно.
Если
a
b
> 900
Слайд 14
Пусть векторы заданы своими координатами a ( x1; y1;
a 2 = | a |2