- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
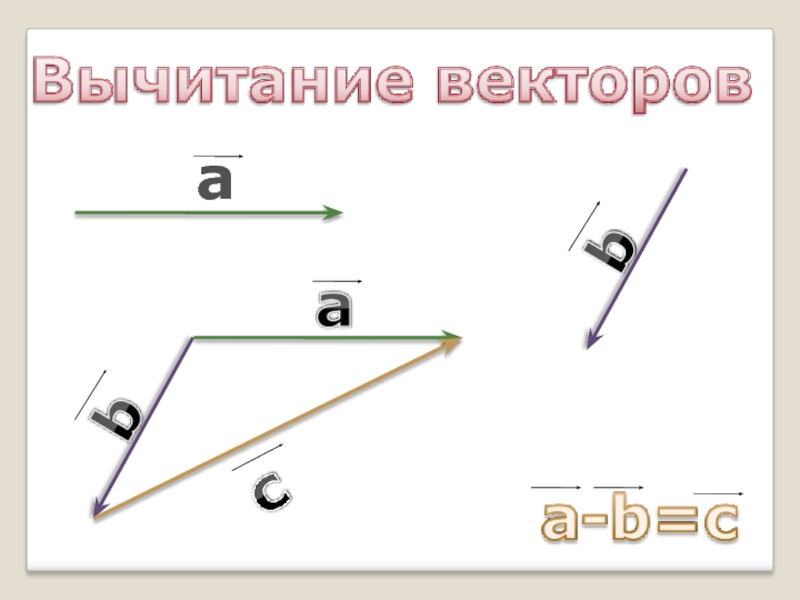
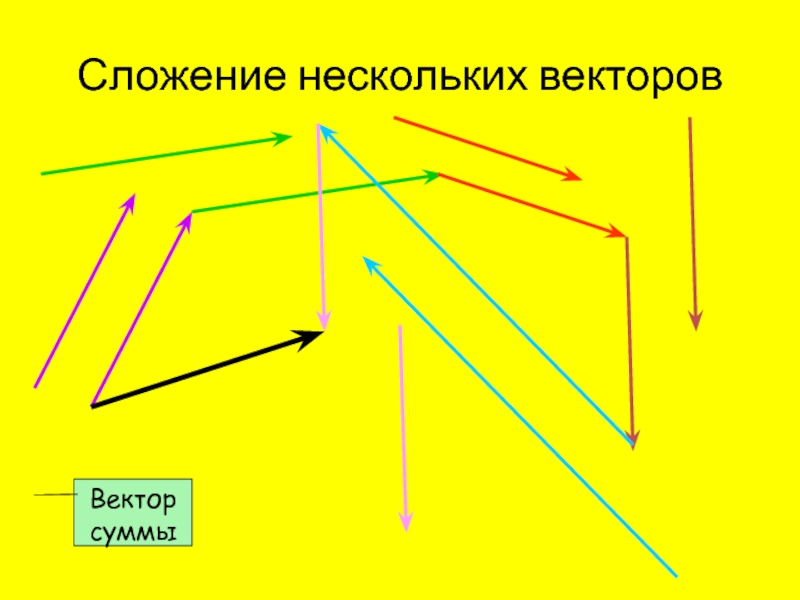
Векторы 9 класс презентация
Содержание
Вектором называется направленный отрезок. Модулем вектора называется длина содержащего его отрезка. l AB l=AB Ненулевые векторы называются коллинеарными, если они лежат либо на одной, либо на
Слайд 2
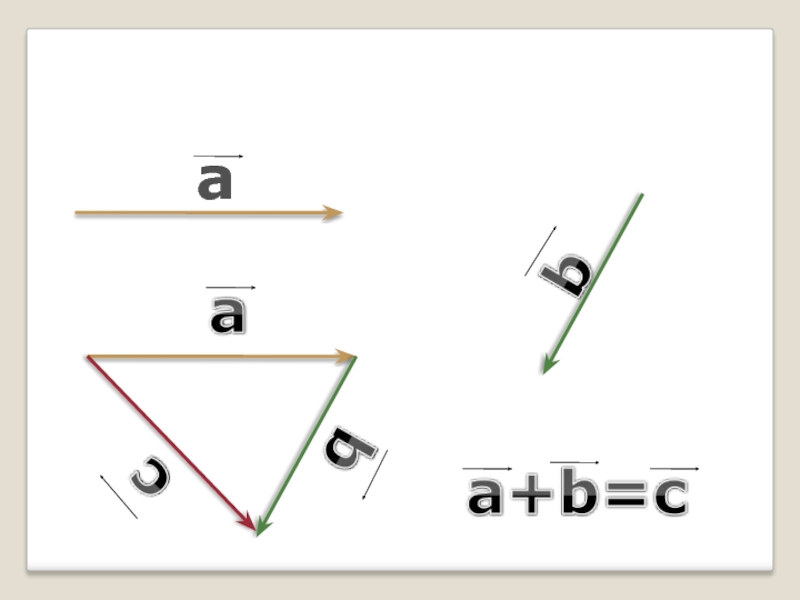
Вектором называется направленный отрезок.
Модулем вектора называется длина содержащего
его отрезка.
l AB l=AB
l AB l=AB
Ненулевые векторы называются коллинеарными, если они лежат
либо на одной, либо на параллельных прямых.
Слайд 3
От любой точки можно отложить вектор равный данному , притом только
один .
g
f
M
B
Откладывание векторов от данной точки
f = g
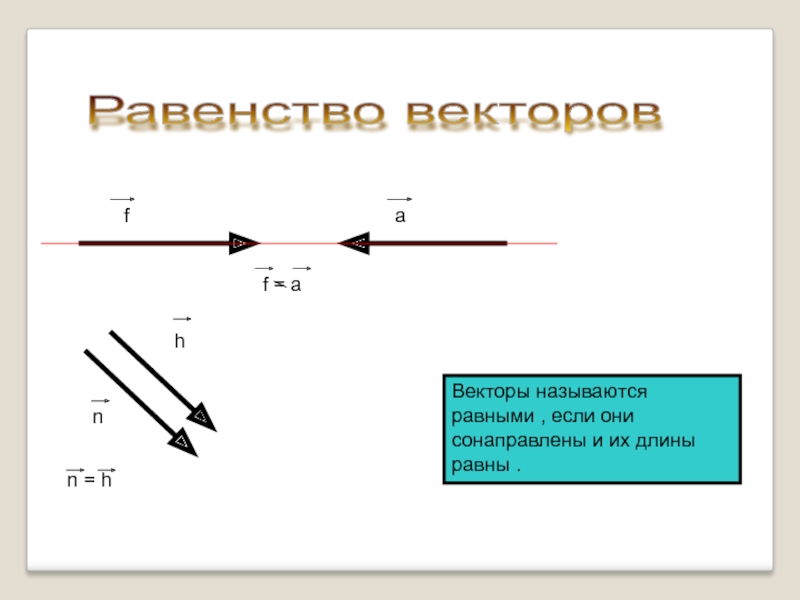
Слайд 4f
a
h
n
Векторы называются равными , если они сонаправлены и их длины равны
.
n = h
f = a
Равенство векторов
Слайд 6
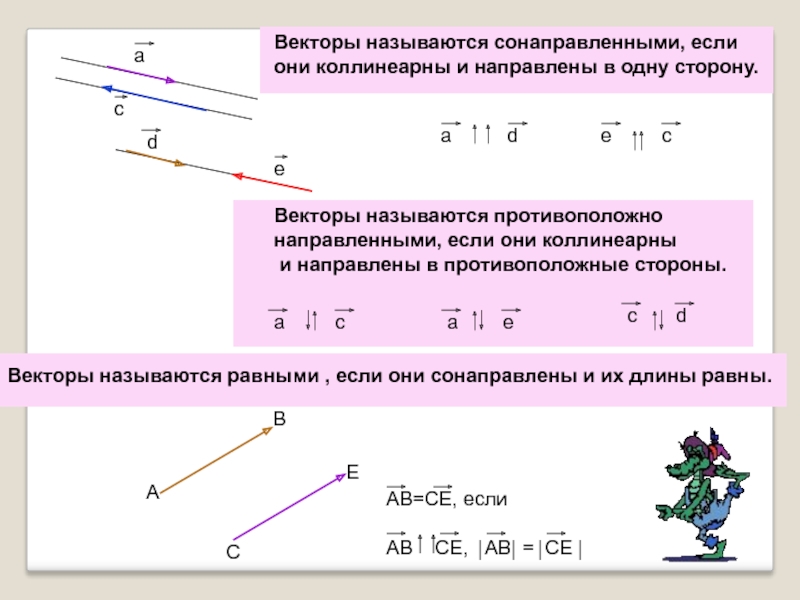
Векторы называются сонаправленными, если
они коллинеарны и направлены в одну сторону.
Векторы называются
противоположно
направленными, если они коллинеарны
и направлены в противоположные стороны.
направленными, если они коллинеарны
и направлены в противоположные стороны.
Векторы называются равными , если они сонаправлены и их длины равны.
А
В
С
Е
Слайд 11Для любых чисел k , l и любых векторов a ,
b справедливы равенства :
(kl )a = k (la ) ( сочетательный закон )
(k+l) a = ka + la ( первый распределительный закон )
K ( a+b ) = ka + kb (второй распределительный закон ) .
(kl )a = k (la ) ( сочетательный закон )
(k+l) a = ka + la ( первый распределительный закон )
K ( a+b ) = ka + kb (второй распределительный закон ) .
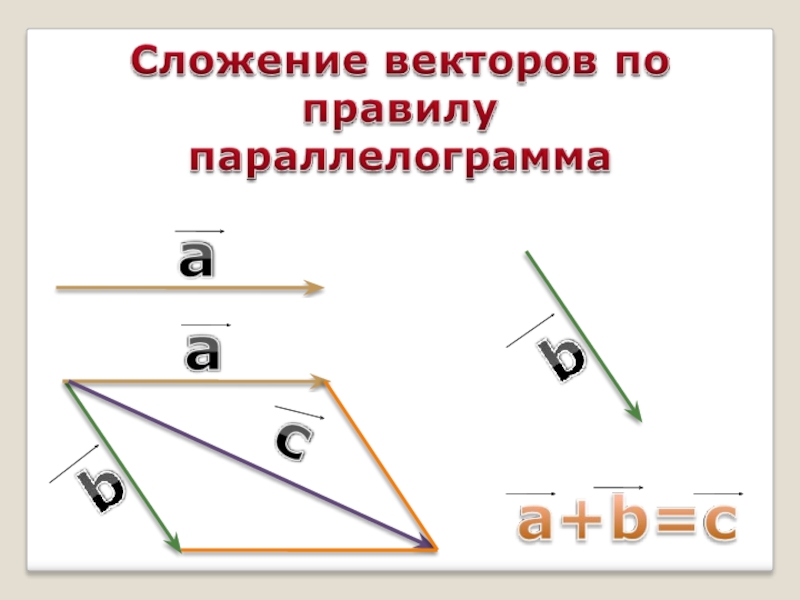
3а
2а
а
Умножение вектора на число
Для любых чисел k , l и любых векторов a , b справедливы равенства :
(kl )a = k (la ) ( сочетательный закон )
(k+l) a = ka + la ( первый распределительный закон )
K ( a+b ) = ka + kb (второй распределительный закон ) .
