- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Векторная алгебра презентация
Содержание
- 1. Векторная алгебра
- 2. Векторная алгебра Определение
- 3. Векторная алгебра Определение
- 4. Векторная алгебра Если
- 5. Векторная алгебра Пусть
- 6. Векторная алгебра
- 7. Действия сложения векторов
- 8. Векторы
- 9. Пример Рассмотрим
- 10. Пример Проверим,
- 11. Пример Получена система
- 12. Пример Вектора
- 13. Векторная алгебра Пусть
- 14. Векторная алгебра
- 15. Векторная алгебра
- 16. Векторная алгебра Общий
- 17. Векторная алгебра По правилу сложению векторов Таким образом, разложение (2) существует
- 18. Векторная алгебра 1)
- 19. Векторная алгебра Таким
- 20. Векторная алгебра Пусть
Слайд 1
Векторная алгебра
Определение вектора, единичного вектора, орта вектора, коллинеарных / компланарных
Проекция вектора на координатные оси
Линейные операции над векторами
Определение линейно зависимых/независимых векторов
Теорема о разложении вектора на плоскости и в пространстве
Слайд 2
Векторная алгебра
Определение
Вектором называется направленный отрезок
Обозначение вектора:
- длина вектора
Определение
Вектор, длина которого равна
называется единичным вектором
Слайд 3
Векторная алгебра
Определение
Единичный вектор, направление которого
совпадает с направлением вектора
ортом вектора и обозначается
Определение
Три вектора в пространстве называются
комплонарными, если они лежат в одной плоскости
или в параллельных плоскостях
Определение
коллинеарных векторов
Слайд 4
Векторная алгебра
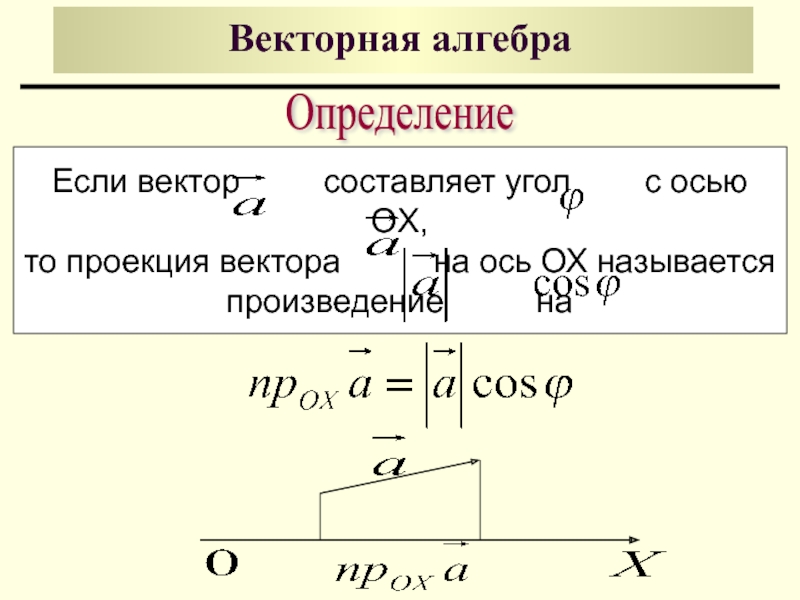
Если вектор составляет угол
то проекция вектора на ось ОХ называется
произведение на
Определение
Слайд 5
Векторная алгебра
Пусть в 3-х-мерном пространстве задана прямоугольная система координат OXYZ
Пусть
Углы, образованные
вектором с
осями координат:
Слайд 6
Векторная алгебра
Проекция вектора на оси координат
Вектор
в прямоугольной системе координат ОXYZ или где
- единичные векторы координатных осей
- длина вектора
- направляющие косинусы вектора
Слайд 7Действия сложения векторов
умножения вектора на число называются
линейными операциями над векторами
Векторная алгебра
Пусть - векторы, заданные на
плоскости или в пространстве
Выражение вида
где -произвольные действительные числа
называется линейной комбинацией векторов
Слайд 8Векторы
зависимыми, если существуют такие
действительные числа одновременно
не обращающиеся в ноль , что линейная
комбинация векторов с этими числами равна
нулевому вектору
Векторная алгебра
Определение
Если равенство (1) выполняется только в случае,
когда , то вектора
называются линейно независимыми
Слайд 9
Пример
Рассмотрим на плоскости два неколлинеарных вектора и
Покажем, что эти векторы линейно независимы
(метод от противного)
Доказательство
Предположим, что вектора линейно зависимы. По определению линейно зависимых
векторов
Для определенности предположим , тогда
Таким образом,
Противоречие! Предположение не верно
Слайд 10
Пример
Проверим, являются ли линейно зависимыми вектора
По определению линейно (не)зависимых векторов
Запишем это
Слайд 11
Пример
Получена система линейных однородных уравнений относительно неизвестных
Если ранг матрицы системы меньше 3, то система имеет ненулевое решение вектора
линейно зависимы
Если ранг равен 3, то система имеет только тривиальное решение вектора
линейно независимы
Слайд 13
Векторная алгебра
Пусть - неколлинеарные
плоскости, тогда всякий комплонарный им вектор
можно представить и притом единственным
образом в виде линейной комбинации векторов
и , то есть , что
Теорема
(о разложении вектора на плоскости)
(2)
Слайд 14
Векторная алгебра
Доказательство
1) Покажем существование разложения
По условию векторы
В случае, если
тогда разложение (2) справедливо при
Слайд 15
Векторная алгебра
В случае, если
тогда разложение (2) справедливо при
Одновременное выполнение
не может
Слайд 16
Векторная алгебра
Общий случай, когда вектора
неколлинеарные.
Приведем к общему началу и построим параллелограмм так, чтобы вектор
был его диагональю, то есть выполним построение
Слайд 18
Векторная алгебра
1) Докажем единственность разложения (2)
Предположим противное, что разложение (2) не
(3)
Вычтем из (2) разложение (3)
при
(*)
Слайд 19
Векторная алгебра
Таким образом, существует такое число
что выполняется (*)
коллинеарные, что противоречит условию теоремы Разложение (2) единственно
Ч.Т.Д.
Слайд 20
Векторная алгебра
Пусть
пространстве , тогда любой вектор
единственным образом разлагается в их
линейную комбинацию, то есть
Теорема
(о разложении вектора в пространстве )
(4)