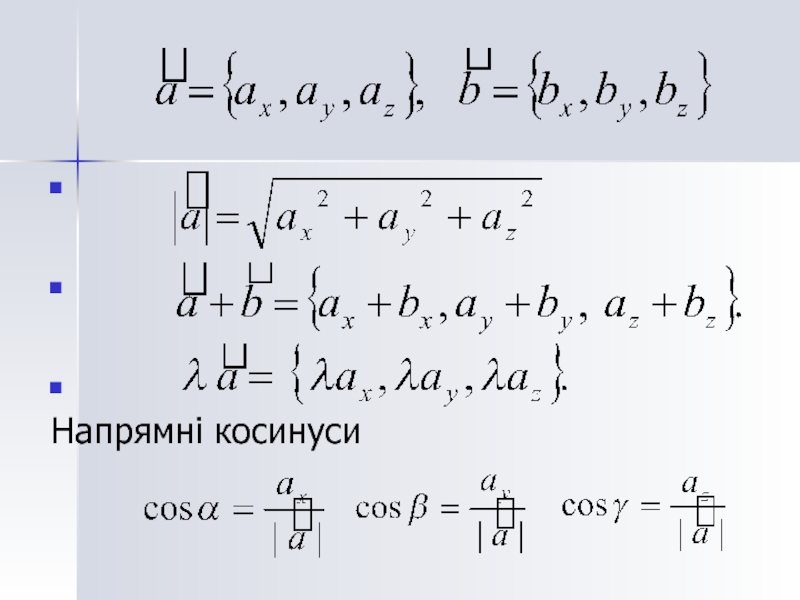- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Векторні величини. Метод координат презентация
Содержание
- 1. Векторні величини. Метод координат
- 2. План Лінійні операції над векторами Проекція вектора
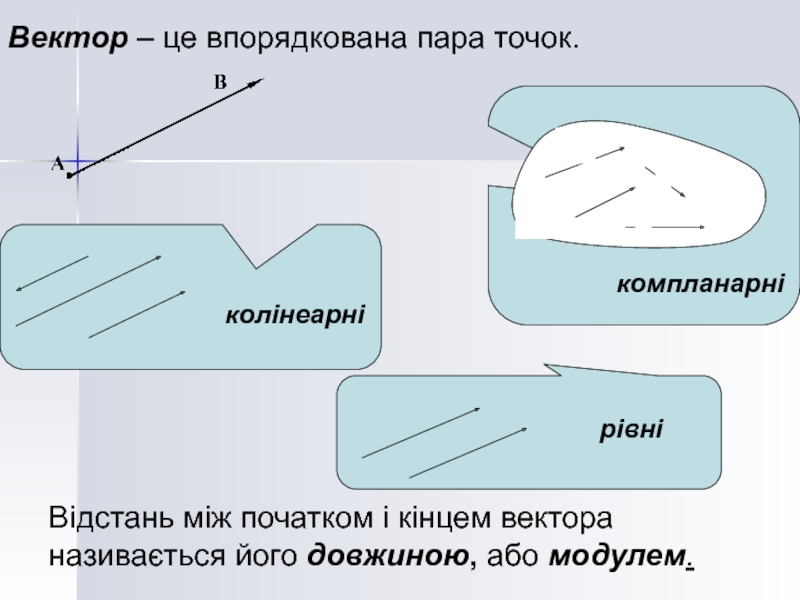
- 3. Вектор – це впорядкована пара точок.
- 4. Лінійні операції над векторами Добуток вектора
- 7. Властивості:
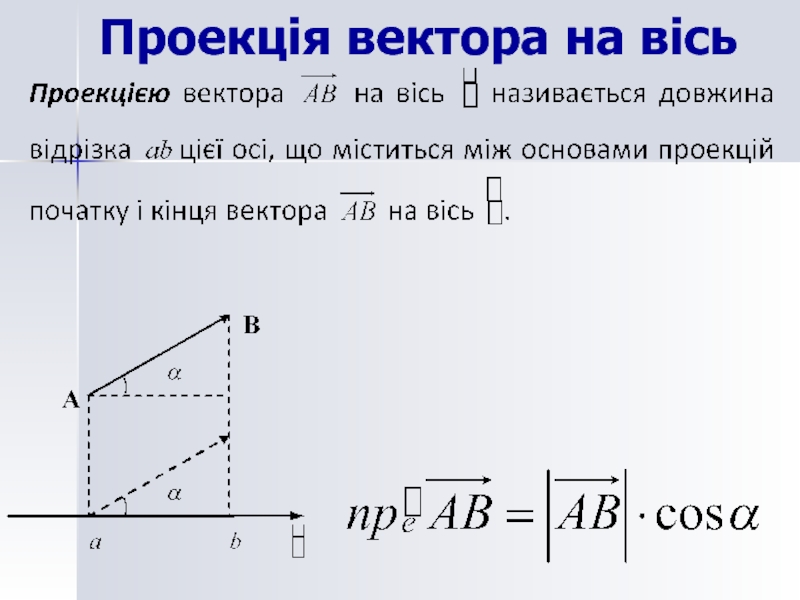
- 9. Проекція вектора на вісь
- 10. Властивості : рівні вектори мають рівні
- 11. Означення
- 12. Теорема Якщо система векторів лінійно залежна, то
- 13. Означення
- 14. Теорема . Довільні два колінеарні вектори лінійно
- 15. Базисом на прямій називається будь-який ненульовий
- 16. Теорема
- 17. Теорема
- 18. Означення
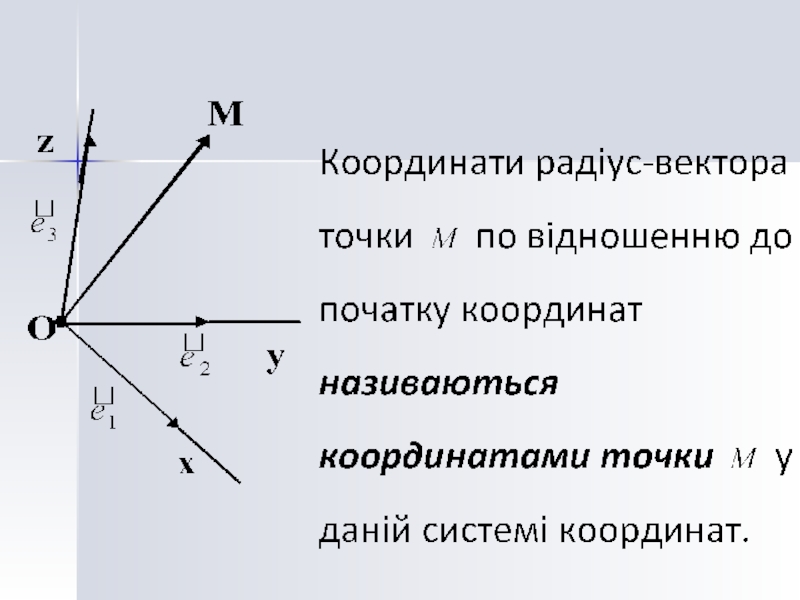
- 19. Декартова системи координат
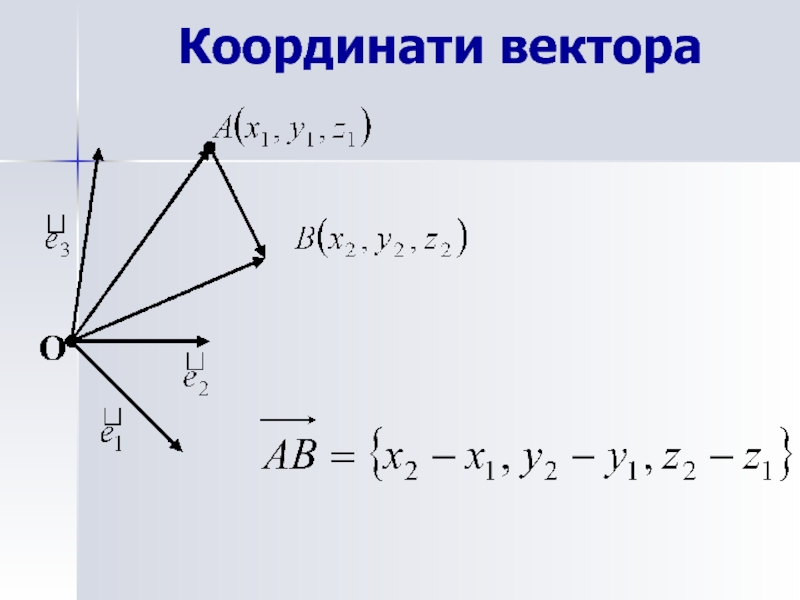
- 21. Координати вектора
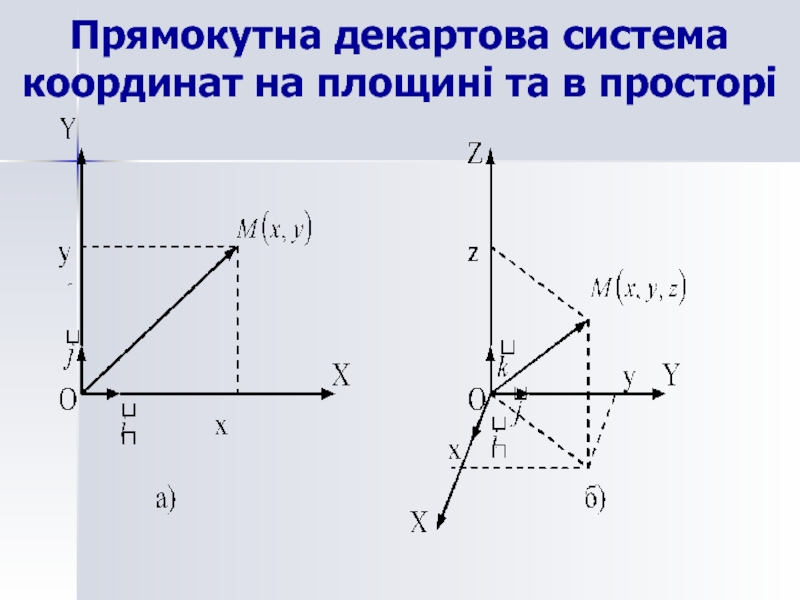
- 24. Прямокутна декартова система координат на площині та в просторі
- 25. Відстань між двома точками На площині В просторі
- 27. Ділення відрізка в заданому відношенні Якщо Та
- 28. Означення
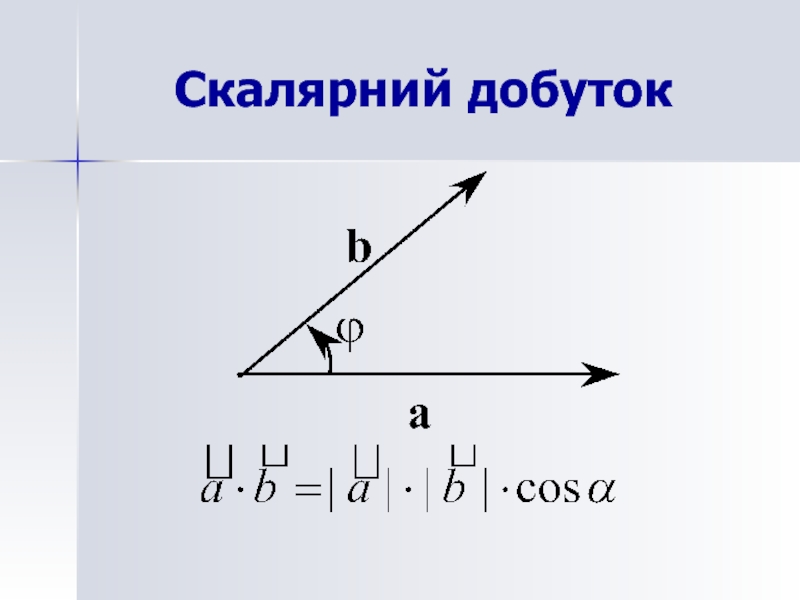
- 29. Скалярний добуток
- 30. властивості:
- 32. Вираз скалярного добутку через координати Якщо
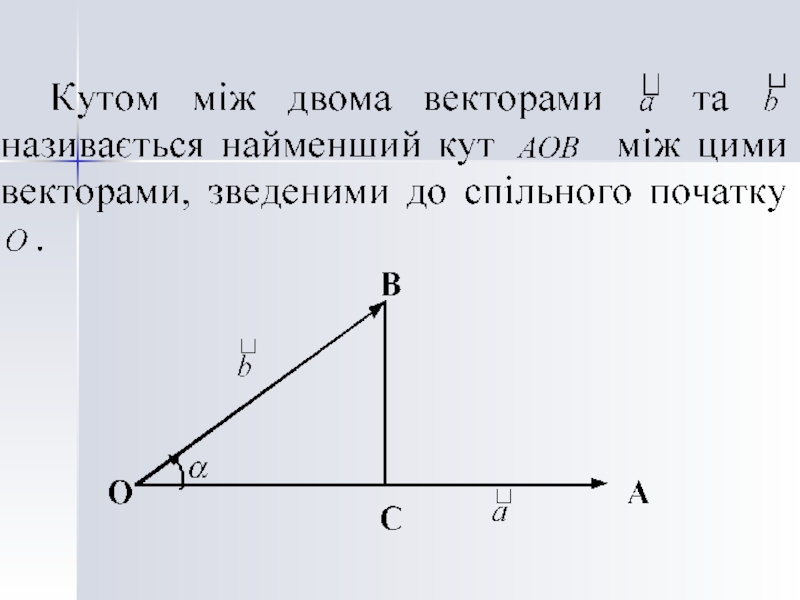
- 33. Застосування: 1. Кут між векторами
- 34. 2. Умова ортогональності двох векторів
- 35. 3. Фізичний зміст якщо матеріальна точка, на
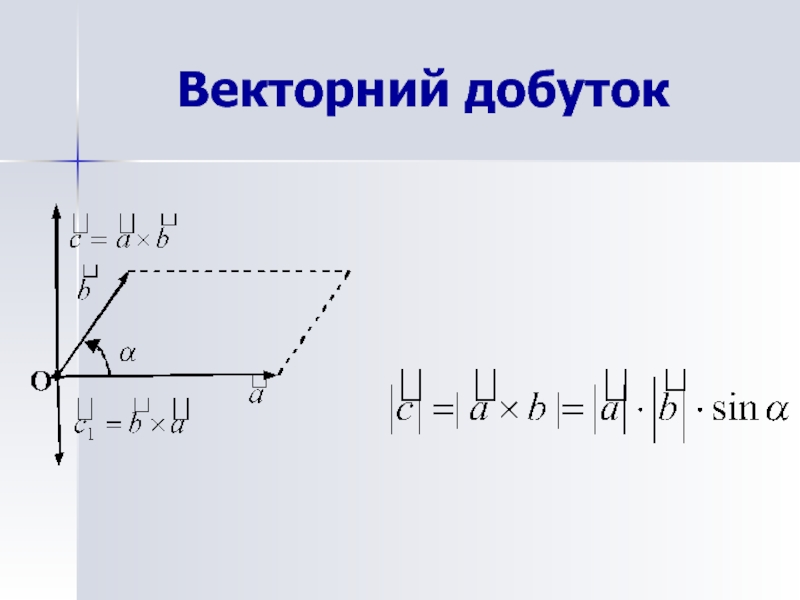
- 37. Векторний добуток
- 38. Властивості:
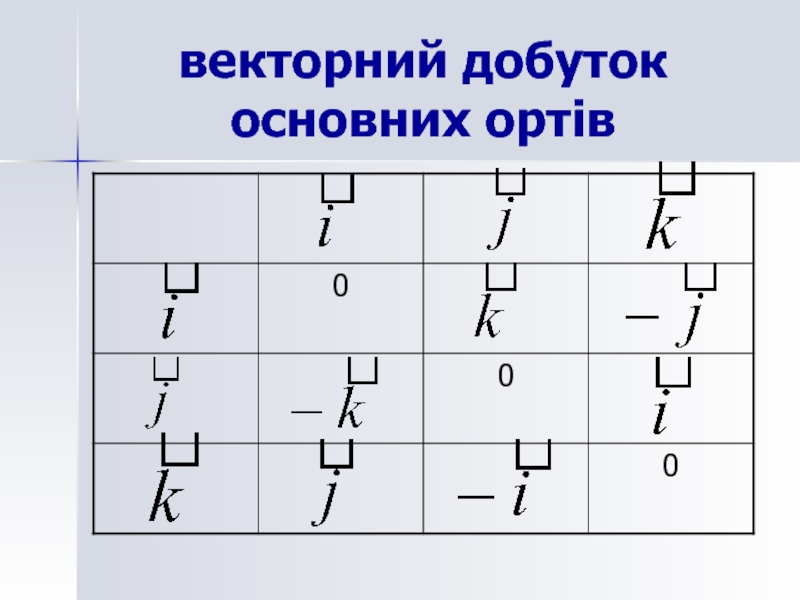
- 39. векторний добуток основних ортів
- 40. Вираз векторного добутку через координати Якщо
- 41. Застосування: 1. умова колінеарності векторів
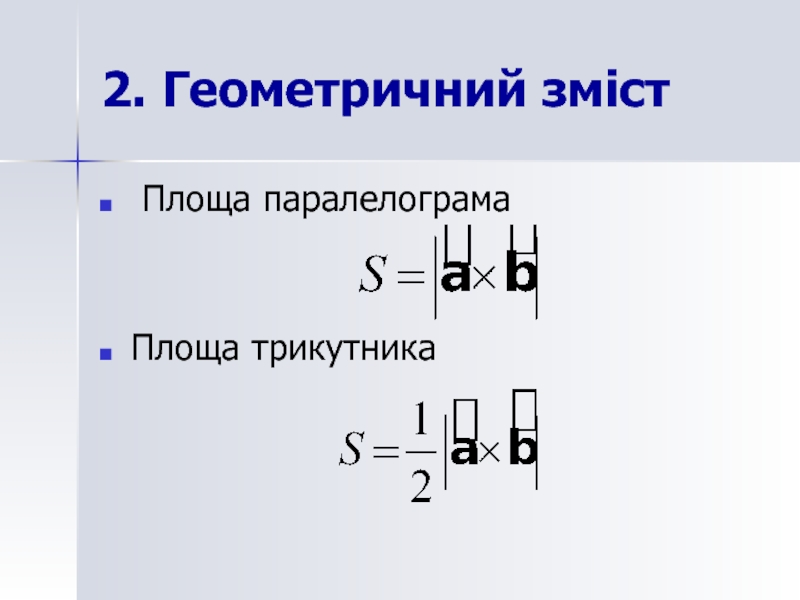
- 42. 2. Геометричний зміст Площа паралелограма Площа трикутника
- 43. 3. Фізичний зміст Момент сили
- 44. Мішаний добуток трьох векторів
- 45. Геометричний зміст
- 47. Умова компланарності
- 48. Властивості:
- 49. Подвійний векторний добуток
- 50. Завдання на самопідготовку Законспектувати і вивчити
Слайд 2План
Лінійні операції над векторами
Проекція вектора на вісь
Лінійна залежність та
незалежність векторів
Метод
Слайд 3Вектор – це впорядкована пара точок.
Відстань між початком і кінцем
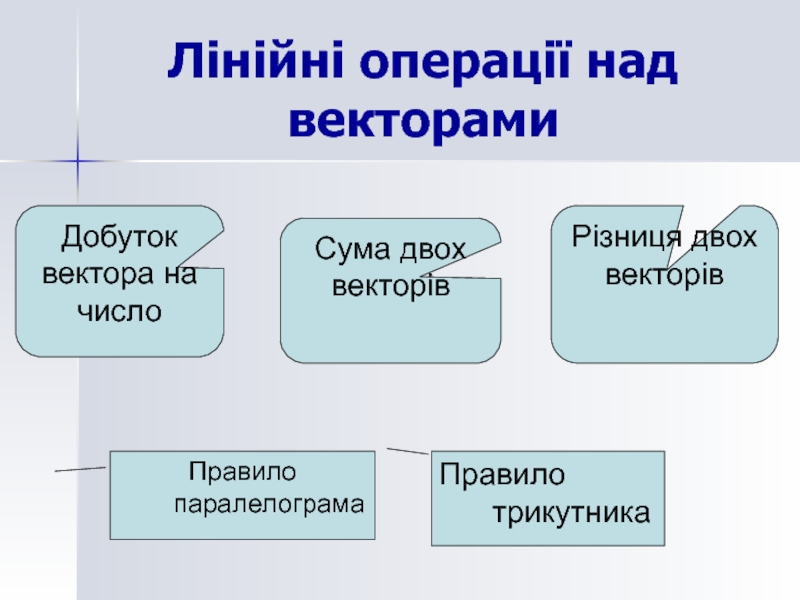
Слайд 4Лінійні операції над векторами
Добуток вектора на число
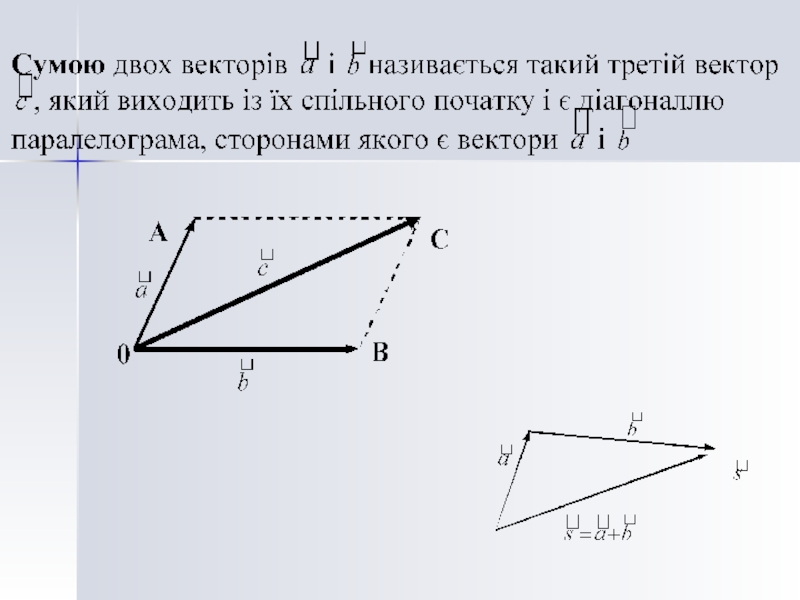
Сума двох векторів
Різниця двох
Правило паралелограма
Правило трикутника
Слайд 7Властивості:
- асоціативність;
- дистрибутивність по відношенню до множення на число
Слайд 10Властивості :
рівні вектори мають рівні проекції;
при множенні вектора
проекція суми двох векторів на вісь дорівнює сумі проекцій цих векторів
Слайд 12Теорема Якщо система векторів лінійно залежна, то хоча би один з
Теорема (обернена). Якщо один з векторів даної системи можна представити у вигляді лінійної комбінації інших, то така система векторів лінійно залежна.
Слайд 14Теорема . Довільні два колінеарні вектори лінійно залежні і, навпаки, два
Теорема . Три компланарних вектори лінійно залежні і, навпаки, три некомпланарних вектори лінійно незалежні.
Теорема . Довільні три ненульові вектори на площині є лінійно залежними.
Теорема . Довільні чотири вектори у просторі лінійно залежні.
Слайд 15 Базисом на прямій називається будь-який ненульовий вектор на цій прямій.
Базисом
Базисом на площині називаються два не колінеарні вектори зі спільним початком на цій площині, взяті в певному порядку.
Слайд 353. Фізичний зміст
якщо матеріальна точка, на яку діє сила, здійснила переміщення
То робота дорівнює скалярному добутку сили на переміщення
Слайд 38Властивості:
асоціативність відносно скалярного множника;
дистрибутивність відносно додавання;
означає колінеарність векторів і .
Слайд 50Завдання на самопідготовку
Законспектувати і вивчити слайди:
5-10, 19-27, 30-31, 33-35.
Шумко Л.І. ,
§2.1-2.5.