- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Вариациялық қатардың сандық сипаттамалары презентация
Содержание
- 1. Вариациялық қатардың сандық сипаттамалары
- 2. Жоспар: Вариациялық қатар дегеніміз не? Вариациялық
- 3. Статистика кең мағынада, табиғат пен қоғамның көптеген
- 4. Статистикалық жиынтық – дегеніміз белгілі бір кеңістікте
- 5. Белгілі бір іріктеуде әрбір вариантаның неше рет
- 6. Вариация өлшемі деп бегінің ауытқушылығын көрсететін абсолюттік
- 7. Вариациялық қатар — зерттелетін белгінің сандық мелшерлерін
- 8. Жұп сандағы реттелген қатардың медианасы деп қатардың ортасында орналасқан екі варианттың бірінің орташа арифметикалығын айтады.
- 10. ПОЛИГОН – дискреттік және интервалдық қатарларды бейнелеуге
- 12. Жиілікті (ni) есептеу үшін СТАТИСТИЧЕСКИЕ категориясынан -
- 13. Сурет 1.2 - Дискретті үлестірім қатар Қатардың
- 14. Орташа квадраттық ауытқу – СТАНДОТКЛОНП функциясы
- 17. Статистикалық талдаудың бірінші кезеңінде зерттелініп жатқан бірліктер
- 18. Есептің қойылуы: Қостанай облысы бойынша негізгі тамақ
- 19. Тапсырма: 1.1 кестедегі мәліметтер бойынша дискреттік вариациялық
- 20. Дискреттік қатарды кесте ретінде анықтаймыз: берілген сиыр
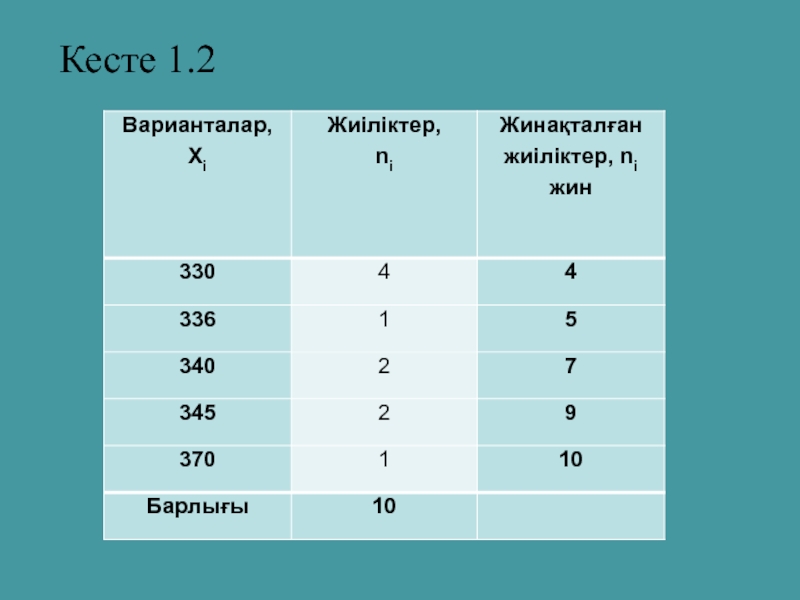
- 21. Кесте 1.2
- 22. Қатардың көрсеткіштерін есептейміз: Вариациялық қатарларды талдау көрсеткіштері
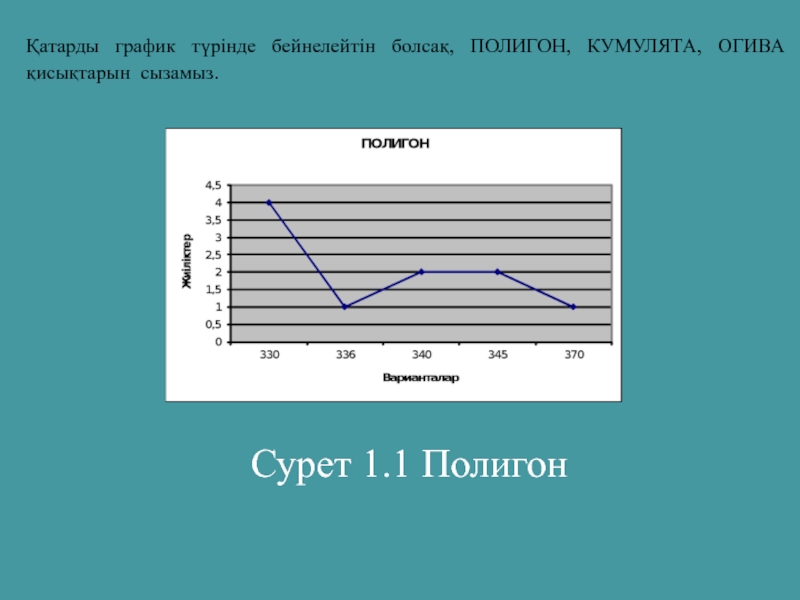
- 26. Қатарды график түрiнде бейнелейтiн болсақ, ПОЛИГОН, КУМУЛЯТА, ОГИВА қисықтарын сызамыз. Сурет 1.1 Полигон
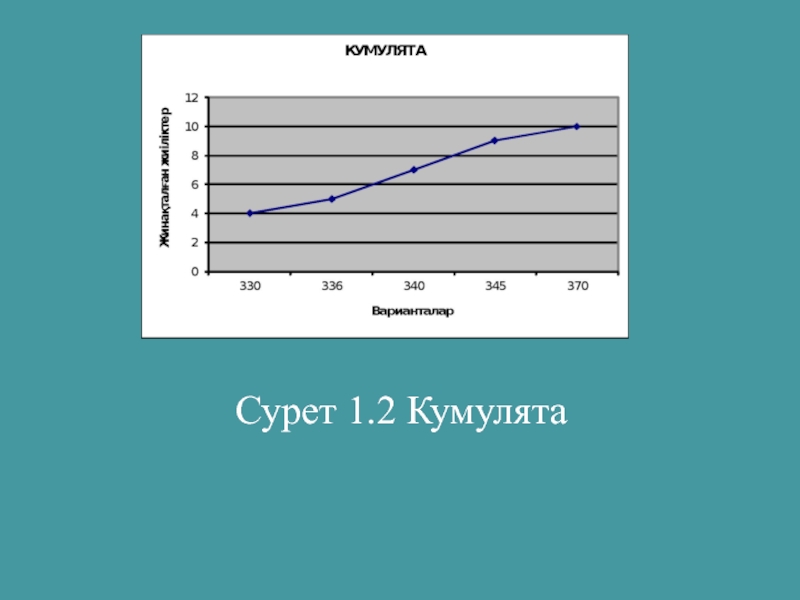
- 27. Сурет 1.2 Кумулята
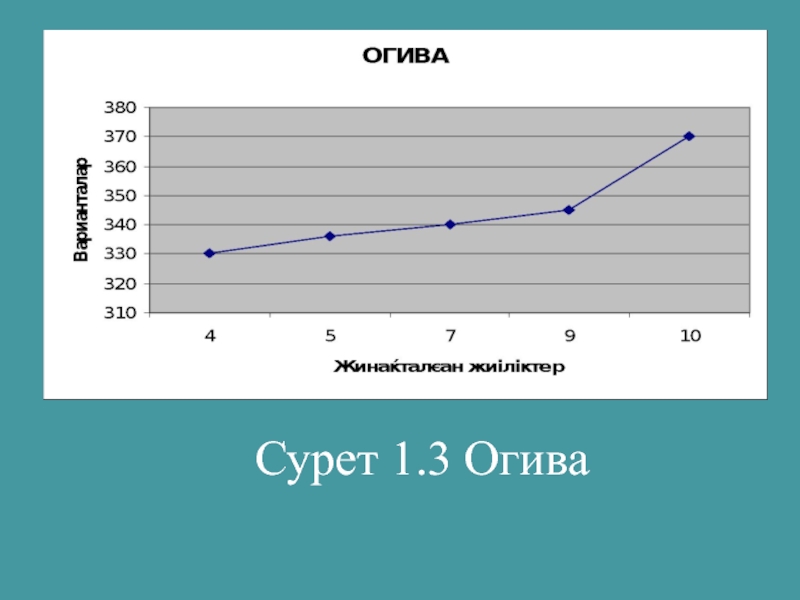
- 28. Сурет 1.3 Огива
- 29. Қорытынды: қарастырылып жатқан жиынтықта сиыр етінің орташа
- 30. Пайдаланған әдебиеттер: 1. Ә.Н.Шыныбеков.Ықтималдықтар теориясы және математикалық
Слайд 2 Жоспар:
Вариациялық қатар дегеніміз не?
Вариациялық қатарды сипаттайтын белгілер?
Қандай жағдайда жай вариациялық
Топтастырылған вариациялық қатар қандай жағдайда құрады?
Топтастырылған вариациялық қатар құру кезеңдері?
Топтастырылған вариациялық қатарда топ саны қалай анықталады?
Вариантаның топ аралығы қалай табылады?
Статистикалық өлшемдер
Слайд 3Статистика кең мағынада, табиғат пен қоғамның көптеген құбылыстарының сапалық ерекшеліктерін айқындау
Слайд 4Статистикалық жиынтық – дегеніміз белгілі бір кеңістікте жəне уақытта алынған салыстырмалы біртекті
Слайд 5Белгілі бір іріктеуде әрбір вариантаның неше рет кездесетіндігін көрсететін сан жиілік
Вариация – жиынтықтың жеке бірліктерінің белгісі мәнінің аутқуы, әртүрлілігі, өзгерілуі.
Вариация деп зерттелетін жиынтықтың кез-келген бірлігі белгісі мәнінің бір кезеңдегі және мезеттегі құбылмалылығын айтады.
Вариация мәні:
Оның өзгеруі басқа өзгермелі белгілердің сол белгіге әсер ету деңгейін бағалауға мүмкіндік береді.
Статистикалық моделбдерді құруда қолданылады.
Слайд 6Вариация өлшемі деп бегінің ауытқушылығын көрсететін абсолюттік және қатысты көрсеткіштерді айтады.
Жиынтықтағы варианталарды зерттеу үшін, оларды вариациялық қатарлар ретінде жазады. Вариациялық қатардағы ең көп кездесетін вариантаны мода деп атайды. Вариациялық қатардың ортасында орналасқан варианта медиана деп аталады. Мода Мо, ал медиана Ме белгілерімен белгіленеді.
Слайд 7Вариациялық қатар — зерттелетін белгінің сандық мелшерлерін жоғарылату немесе темендету ретімен орналастыру.
Вариациялық қатардың құрылымдық сипаттамасына: мода, медиана, децили, квартили, перцентили жатады.
Мода деп – зерттелетін жиынтықта басқаларына қарағанда жиі кездесетін вариантаны айтады.
Дискреттік қатарда мода деп – көп рет кездесетін белгіні айтады. Мода мысалы, сатып алушыларда үлкен сұранысқа ие киім мен аяқ киімінің размерін анықтау үшін жиі қолданылады.
Интервалды вариацияның қатарда моданы есептеу үшін алдымен мода орналасқан модальді интервалды анықтау керек, ал одан кейін белгінің модальді шамасының мәнін анықтау керек.
Медиана (Ме) - белгілі бір тәртіппен орналасқан, өсуі бойынша немесе азаюы бойынша реттелген қатардың варианттарының бірінің орташасы. Ол мұндай қатарды ортасынан бөледі. Медиананы табу үшін реттелген қатардың ортасында орналасқан белгінің мәнін табу керек. Тақ қатардағы реттелген қатардың медианасы деп ортасында тұрған белгінің шамасын айтады. Тақ қатардағы реттелген қатардың медианасы номері келесі формуламен есептеледі:
Слайд 8Жұп сандағы реттелген қатардың медианасы деп қатардың ортасында орналасқан екі варианттың
Слайд 10ПОЛИГОН – дискреттік және интервалдық қатарларды бейнелеуге арналған график. Координаталар жүйесінде
ГИСТОГРАММА – тек қана интервалдық қатарды бейнелейді. Координаталар жүйесінде Х бойымен интервалдар, У бойымен жиіліктер алынады.
КУМУЛЯТА – жинақталған жиіліктер қисығы. Координаталар жүйесінде Х бойымен варианталар, У бойымен жинақталған жиіліктер алынады.
ОГИВА – кумулятаға керісінше, Х бойымен жинақталған жиіліктер, У бойымен варианталар алынады.
Слайд 11
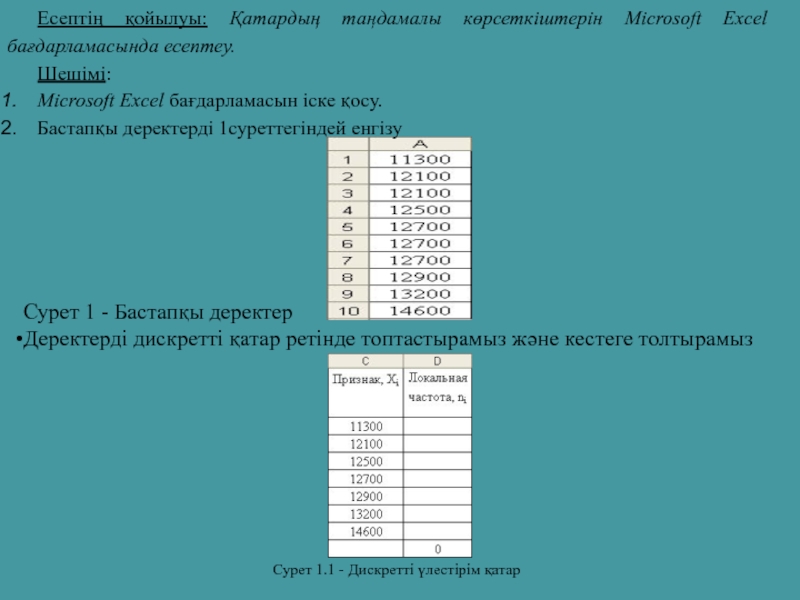
Сурет 1 - Бастапқы деректер
Деректерді дискретті қатар ретінде топтастырамыз және кестеге
Сурет 1.1 - Дискретті үлестірім қатар
Есептің қойылуы: Қатардың таңдамалы көрсеткіштерін Microsoft Excel бағдарламасында есептеу.
Шешімі:
Microsoft Excel бағдарламасын іске қосу.
Бастапқы деректерді 1суреттегіндей енгізу
Слайд 12Жиілікті (ni) есептеу үшін СТАТИСТИЧЕСКИЕ категориясынан - СЧЕТЕСЛИ функциясын пайдаланамыз.
-
- «Аргументы функции» терезесінде «Диапазон» өрісін А1:А10 ұяшықтар диапазонымен толтыру, «Критерий» өрісінде – 11300 (С2 ұяшығы);
- D3:D8 ұяшықтарына формуланы көшіру
- барлық жиіліктерінің сомасын есептеу (1.2 сурет)
Слайд 13Сурет 1.2 - Дискретті үлестірім қатар
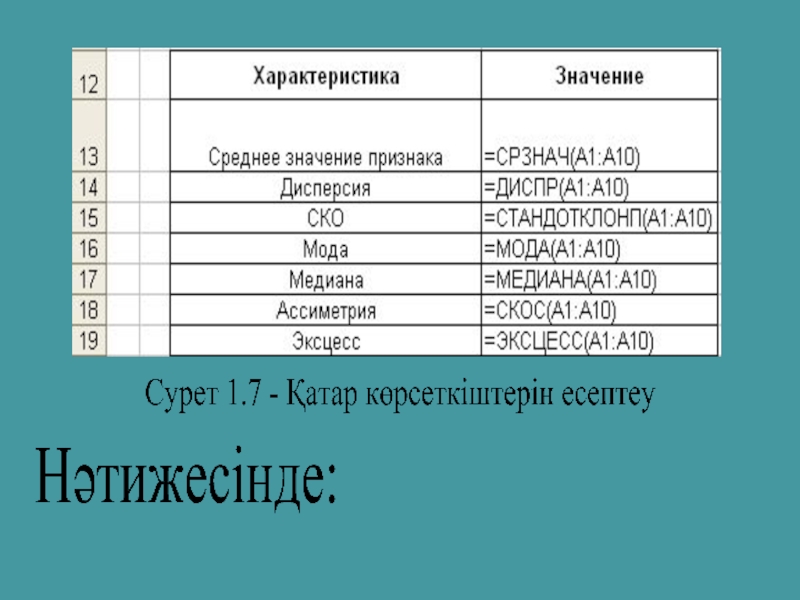
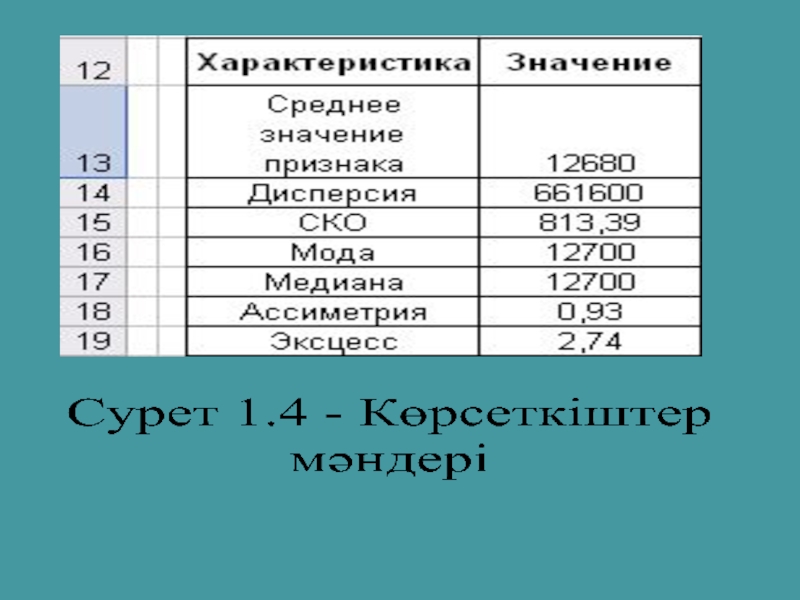
Қатардың көрсеткіштерін есептеу үшін СТАТИСТИЧЕСКИЕ категориясынан
Арифметикалық орташа – СРЗНАЧ функциясы
Дисперсия – ДИСПР функциясы
Слайд 14
Орташа квадраттық ауытқу – СТАНДОТКЛОНП функциясы
Мода – МОДА
Медиана – МЕДИАНА
Ассиметрия коэффициенті
Эксцесс көрсеткіші – ЭКСЦЕСС
Көрсеткіштер мәндерін қосымша кестеге толтыру (1.3 сурет)
Слайд 17Статистикалық талдаудың бірінші кезеңінде зерттелініп жатқан бірліктер бойынша мәліметтер жиналады.
Статистикалық
Жинақтау нәтижелері екі түрлі вариациялық қатарлар ретінде анықталуы мүмкін.
Вариациялық қатарлардың екі түрлерін ажыратады – дискретті және интервалдық.
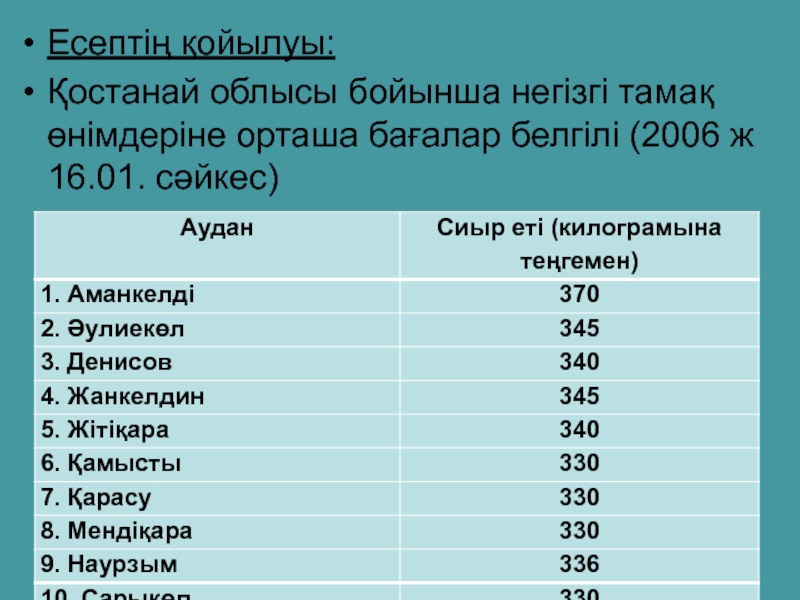
Слайд 18Есептің қойылуы:
Қостанай облысы бойынша негізгі тамақ өнімдеріне орташа бағалар белгілі (2006
Слайд 19Тапсырма: 1.1 кестедегі мәліметтер бойынша дискреттік вариациялық қатар құру, қатардың негізгі
Шешімі:
Дискреттік вариациялық қатарды құру үшін, кестедегі мәліметтерді өсу немесе кему ретімен орналастырамыз: 330, 330, 330, 330, 336, 340, 340, 345, 345, 370.
Слайд 20Дискреттік қатарды кесте ретінде анықтаймыз: берілген сиыр етінің бағасы – варианта,
Слайд 22Қатардың көрсеткіштерін есептейміз: Вариациялық қатарларды талдау көрсеткіштері 4 топқа бөлінеді: 1) Орташа шамалар
Слайд 26Қатарды график түрiнде бейнелейтiн болсақ, ПОЛИГОН, КУМУЛЯТА, ОГИВА қисықтарын сызамыз.
Сурет
Слайд 29Қорытынды: қарастырылып жатқан жиынтықта сиыр етінің орташа бағасы 339,6 теңгеге тең,
Слайд 30Пайдаланған әдебиеттер:
1. Ә.Н.Шыныбеков.Ықтималдықтар теориясы және математикалық статистика элементтері. Оқу құралы.-Алматы:Экономика, 2008.-236
2. Лукьянова Е.А. Медицинская статистика.- М.: Изд. РУДН, 2002.
3. Медик В.А.,Токмачев М.С.,Фишман Б.Б.Статистика в медицине и биологии. М.: Медицина, 2000.
4. И.В. Павлушков и др. Основы высшей математики и математической статистики. (учебник для медицинских и фармацевтических вузов) М., «ГЭОТАР - МЕД»; 2008