- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Устойчивость пластин и оболочек презентация
Содержание
- 1. Устойчивость пластин и оболочек
- 2. Понятие об устойчивости. Задача Эйлера Задача Эйлера
- 3. Понятие об устойчивости. Задача Эйлера Граничные условия 1) 2)
- 4. Понятие об устойчивости. Задача Эйлера
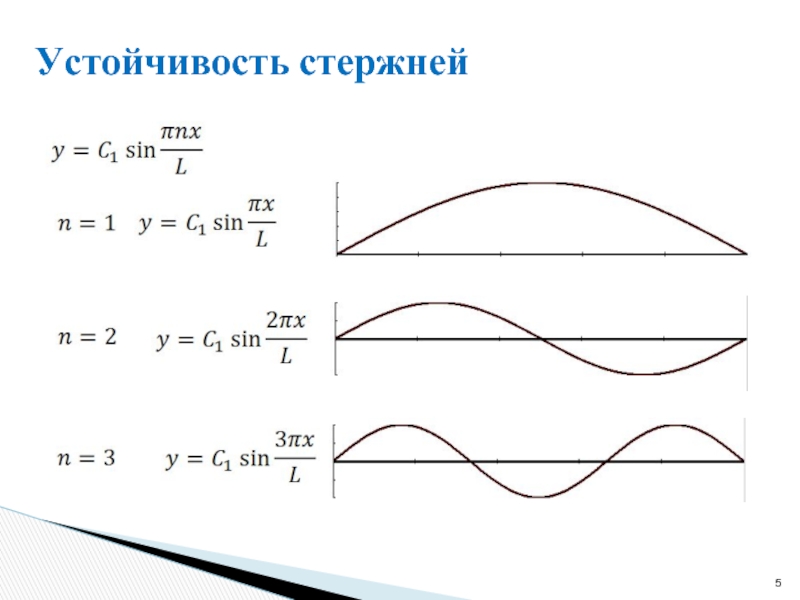
- 5. Устойчивость стержней
- 6. Устойчивость пластин Дифференциальное уравнение изогнутой поверхности пластины
- 7. Устойчивость прямоугольной пластины, свободно опертой по четырем
- 8. Устойчивость прямоугольной пластины, свободно опертой по четырем
- 9. Устойчивость прямоугольной пластины, свободно опертой по четырем
- 10. Устойчивость прямоугольной пластины, свободно опертой по четырем
- 11. Двустороннее сжатие прямоугольной пластины, свободно опертой по
- 12. Двустороннее сжатие прямоугольной пластины, свободно опертой по
- 13. Двустороннее сжатие прямоугольной пластины, свободно опертой по четырем сторонам
- 14. Двустороннее сжатие прямоугольной пластины, свободно опертой по
- 15. Устойчивость оболочек Дифференциальное уравнение для цилиндрической оболочки
- 16. Устойчивость цилиндрической оболочки при осевом сжатии Решение
- 17. Устойчивость цилиндрической оболочки при осевом сжатии Число
- 18. Устойчивость цилиндрической оболочки при осевом сжатии
- 19. Устойчивость цилиндрической оболочки при осевом сжатии Эта формула впервые была получена Лоренцем и Тимошенко (7)
- 20. Устойчивость цилиндрической оболочки при осевом сжатии Экспериментальные
- 21. Устойчивость цилиндрической оболочки при осевом сжатии Влияние внутреннего давления на коэффициент устойчивости
- 22. Устойчивость цилиндрической оболочки при равномерном внешнем давлении
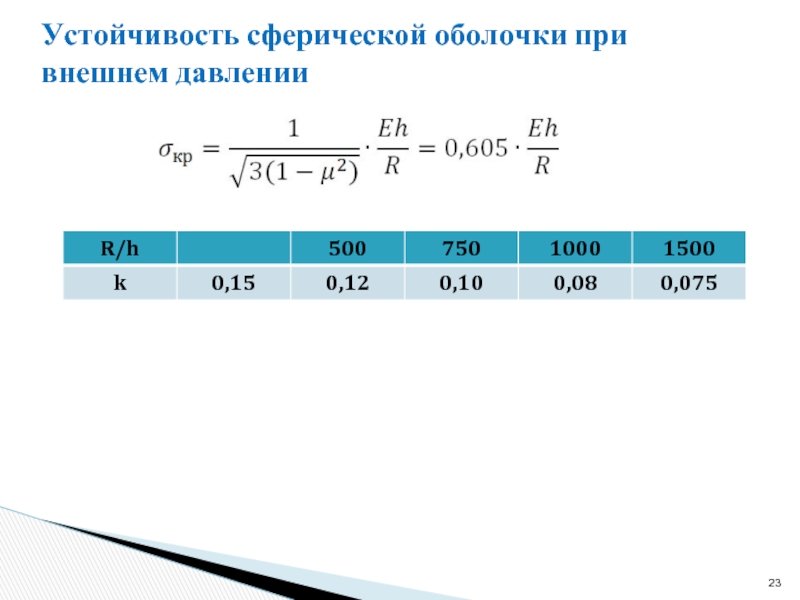
- 23. Устойчивость сферической оболочки при внешнем давлении
- 24. Спасибо за внимание!
Слайд 2Понятие об устойчивости.
Задача Эйлера
Задача Эйлера – задача о равновесии стержня, сжатого
Под устойчивостью понимается свойство системы самостоятельно восстанавливать свое первоначальное состояние после того, как ей было сообщено некоторое отклонение от положения равновесия.
При малых прогибах
Изгиб стержня происходит в плоскости минимальной жесткости и поэтому под величиной I понимается минимальный момент инерции сечения.
Слайд 6Устойчивость пластин
Дифференциальное уравнение изогнутой поверхности пластины при действии сил в срединной
Это уравнение следует использовать в том случае, если пластина, кроме поперечных нагрузок подвергается еще и действию сил в ее срединной плоскости.
(1)
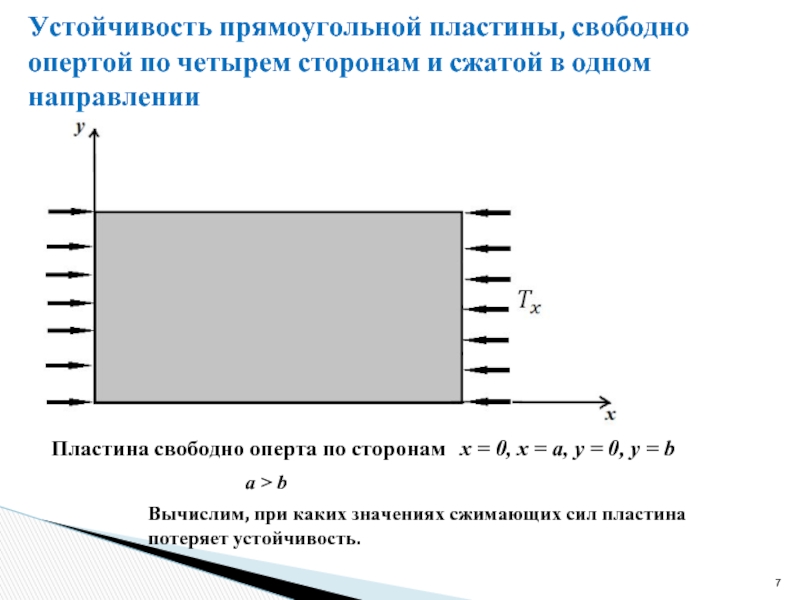
Слайд 7Устойчивость прямоугольной пластины, свободно опертой по четырем сторонам и сжатой в
Пластина свободно оперта по сторонам x = 0, x = a, y = 0, y = b
a > b
Вычислим, при каких значениях сжимающих сил пластина потеряет устойчивость.
Слайд 8Устойчивость прямоугольной пластины, свободно опертой по четырем сторонам и сжатой в
Предположим, что выпучивание пластины происходит по уравнению
(2)
Уравнение (2) удовлетворяет граничным условиям
Проверим, удовлетворяет ли решение (2) исходному дифференциальному уравнению (1)
Дифференцируя уравнение (2) получаем:
Слайд 9Устойчивость прямоугольной пластины, свободно опертой по четырем сторонам и сжатой в
Учитывая, что в данном случае
Подставляя производные в дифференциальное уравнение (1), получаем следующее тождество
Откуда
или
(3)
Слайд 10Устойчивость прямоугольной пластины, свободно опертой по четырем сторонам и сжатой в
где
Остается исследовать выражение (3) на минимум. Учитываем, что по смыслу задачи m может принимать только целые положительные значения.
Для квадратной пластины (a=b) минимум получается только при
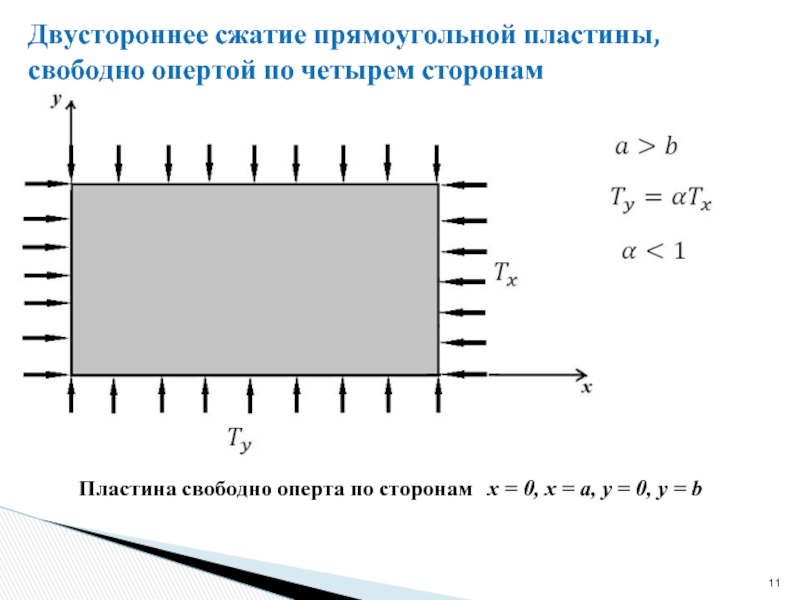
Слайд 11Двустороннее сжатие прямоугольной пластины, свободно опертой по четырем сторонам
Пластина свободно оперта
Слайд 12Двустороннее сжатие прямоугольной пластины, свободно опертой по четырем сторонам
Предположим, что выпучивание
(4)
Дифференцируя (4) и подставляя в дифференциальное уравнение (1), получаем
Слайд 14Двустороннее сжатие прямоугольной пластины, свободно опертой по четырем сторонам
Для квадратной пластины
Наименьшее значение при
По сравнению с 1-м случаем значение критической нагрузки получается в 2 раза меньше
Слайд 15Устойчивость оболочек
Дифференциальное уравнение для цилиндрической оболочки имеет следующий вид
(5)
1. Устойчивость цилиндрической
Граничные условия
Предположим, что края оболочки шарнирно оперты, т.е.
1) При
2) При
Слайд 16Устойчивость цилиндрической оболочки при осевом сжатии
Решение дифференциального уравнения (5), удовлетворяющего граничным
где
Подставляя это решение в дифференциальное уравнение, получим
(6)
Слайд 17Устойчивость цилиндрической оболочки при осевом сжатии
Число полуволн m подбирается из условия
Тонкие оболочки обычно теряю устойчивость с образованием большого числа полуволн.
Обозначив
Можно записать
Слайд 19Устойчивость цилиндрической оболочки при осевом сжатии
Эта формула впервые была получена Лоренцем
(7)
Слайд 20Устойчивость цилиндрической оболочки при осевом сжатии
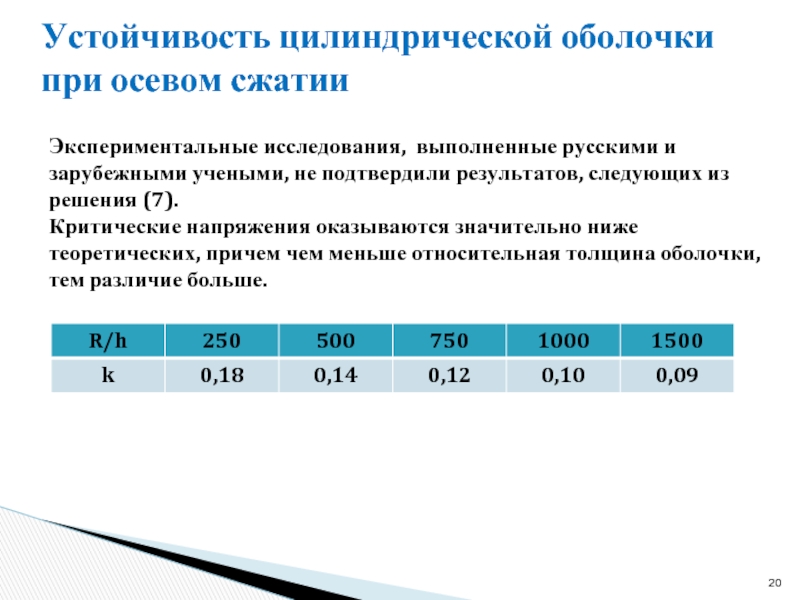
Экспериментальные исследования, выполненные русскими и зарубежными
Критические напряжения оказываются значительно ниже теоретических, причем чем меньше относительная толщина оболочки, тем различие больше.
Слайд 21Устойчивость цилиндрической оболочки при осевом сжатии
Влияние внутреннего давления на коэффициент устойчивости
Слайд 22Устойчивость цилиндрической оболочки при равномерном внешнем давлении
Для оболочки средней длины
Формула оболочки
В расчетах