- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Уравнения и неравенства с параметрами. Часть 1 презентация
Содержание
- 1. Уравнения и неравенства с параметрами. Часть 1
- 2. План Что такое задача с параметром?
- 3. Что такое задача с параметром Задачи:
- 4. Задача с параметром первого типа Пример: Решить
- 5. Задача с параметром первого типа
- 6. Задача с параметром второго типа Примеры
- 7. Методы решения задач с параметрами Аналитические Графические
- 8. Аналитические приемы 1. «В лоб» Этапы:
- 9. Решение «в лоб» Пример Решить уравнение: Решение:
- 10. Решение «в лоб» Квадратное уравнение
- 11. Схема решения 2 этап:
- 12. Схема решения 3 этап. Ответ:
- 13. Решение «в лоб» Замечание.
- 14. Аналитические приемы 2. Метод равносильных переходов Используются
- 15. 2. Метод равносильных переходов Решение:
- 16. Решение при a 1 решений нет при a>1
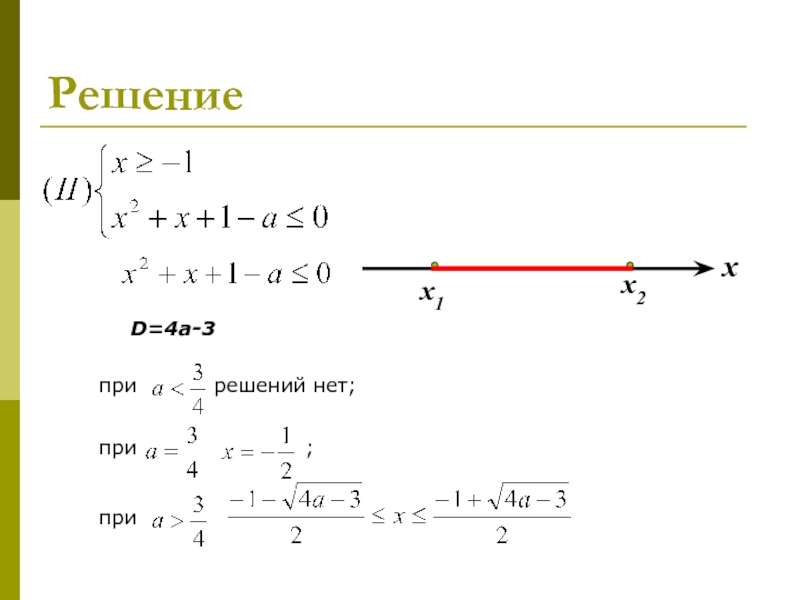
- 17. Решение D=4a-3 х при
- 18. Решение Ответ: при
- 19. Аналитические приемы 3. Замена переменной исходя из свойств какой-то функции упрощающая вычисления
- 20. 3. Замена переменной Пример 1.
- 21. 3. Замена переменной Пример 2. При каких
- 22. Аналитические приемы 4. Использование свойств функций монотонность ограниченность свойства линейной и квадратичной функций
- 23. 4. Использование свойств функций Пример
- 24. 4. Использование свойств функций Пример 2.
- 25. 4. Использование свойств функций Пример 3. Найдите
- 26. Аналитические приемы 5. Поиск необходимых условий использование
- 27. 5. Поиск необходимых условий Пример
- 28. 5. Поиск необходимых условий Пример 2. При
- 29. 6. Рассмотрение параметра как равноправной переменной
- 30. 7. Решение относительно параметра Пример:
- 31. Задание Решите неравенство: 2a(a-2)x>a-2 Решите уравнение:
- 32. Задание 5. Решить уравнение: 6. Решить систему
Слайд 2План
Что такое задача с параметром?
Аналитический метод решения задач с параметрами.
Графический
Слайд 3Что такое задача с параметром
Задачи:
Решить уравнение (найти все пары чисел (х,
Например: решить уравнение в целых числах
Для каждого значения а решить уравнение относительно переменной х.
Слайд 4Задача с параметром первого типа
Пример:
Решить уравнение относительно х:
где b
Семейство уравнений:
Слайд 5Задача с параметром первого типа
Определение
Решить уравнение с
Замечание. Аналогично определяются понятия неравенства, системы уравнений, системы неравенств с параметром. Кроме того, часто встречаются задачи, в условии которых содержится не один, а несколько параметров.
Слайд 6Задача с параметром второго типа
Примеры
Для каких значений a и b
2. При каких значениях а минимум функции больше 1?
Слайд 8Аналитические приемы
1. «В лоб»
Этапы:
- обнаружение критических значений параметра и разбиение
- решение задачи на каждом из выделенных подмножеств
- запись ответа
Слайд 9Решение «в лоб»
Пример
Решить уравнение:
Решение:
1 этап.
1 вывод. Уравнение степени не выше
2 вывод. Рассмотреть значения параметра, влияющие на степень уравнения.
1 промежуточный результат:
Первое «критическое» значение параметра а=1
Слайд 10Решение «в лоб»
Квадратное уравнение
2 промежуточный результат:
Второе «критическое» значение параметра:
Результат
Слайд 11Схема решения
2 этап:
а=-0,8 – дискриминант квадратного уравнения обращается в ноль, и уравнение имеет корень х=
уравнение является квадратным с положительным дискриминантом, и его корнями являются два различных числа:
а=1 – уравнение имеет вид: 6х+7=0 и единственный корень:
Слайд 13Решение «в лоб»
Замечание.
При определении пограничных значений параметра следует
- обращение в 0 старшего коэффициента;
- обращение в 0 дискриминанта;
- границы области определения параметра;
- ОДЗ уравнения (неравенства…) и др.
Слайд 14Аналитические приемы
2. Метод равносильных переходов
Используются теоремы о равносильных и неравносильных преобразованиях
Пример: решить неравенство
Слайд 19Аналитические приемы
3. Замена переменной
исходя из свойств какой-то функции
упрощающая вычисления
Слайд 203. Замена переменной
Пример 1.
При каких значения параметра
ОДЗ:
x=sin(t),
так как , то
Слайд 213. Замена переменной
Пример 2.
При каких значениях параметра с система имеет решение?
(1)
Пусть
, z=4
Слайд 22Аналитические приемы
4. Использование свойств функций
монотонность
ограниченность
свойства линейной и квадратичной функций
Слайд 234. Использование свойств функций
Пример 1. (ограниченность)
При каких
Слайд 244. Использование свойств функций
Пример 2. (монотонность)
При каких значениях
(1)
Слайд 254. Использование свойств функций
Пример 3.
Найдите все значения параметра а, при которых
1 вывод: И
2 вывод:
Слайд 26Аналитические приемы
5. Поиск необходимых условий
использование симметрии аналитических выражений
присутствует требование единственности решения
есть
поиск «выгодной» точки
Слайд 275. Поиск необходимых условий
Пример 1.
При каких значениях
Необходимое условие: х=0.
Слайд 285. Поиск необходимых условий
Пример 2.
При каких значениях параметра а уравнения равносильны?
(1)
(2)
(1)
Слайд 296. Рассмотрение параметра как равноправной переменной
Пример:
Найти все значения параметра,
(1)
(2)
Слайд 307. Решение относительно параметра
Пример:
При каких значениях параметра а
sinx=t
Слайд 31Задание
Решите неравенство: 2a(a-2)x>a-2
Решите уравнение:
Найдите те значения параметра а, при которых
При каких значениях параметра уравнения имеют общие корни?
;
Слайд 32Задание
5. Решить уравнение:
6. Решить систему
уравнений:
7. Найти все значения параметра,
8.При каких значениях а система имеет единственное решение?