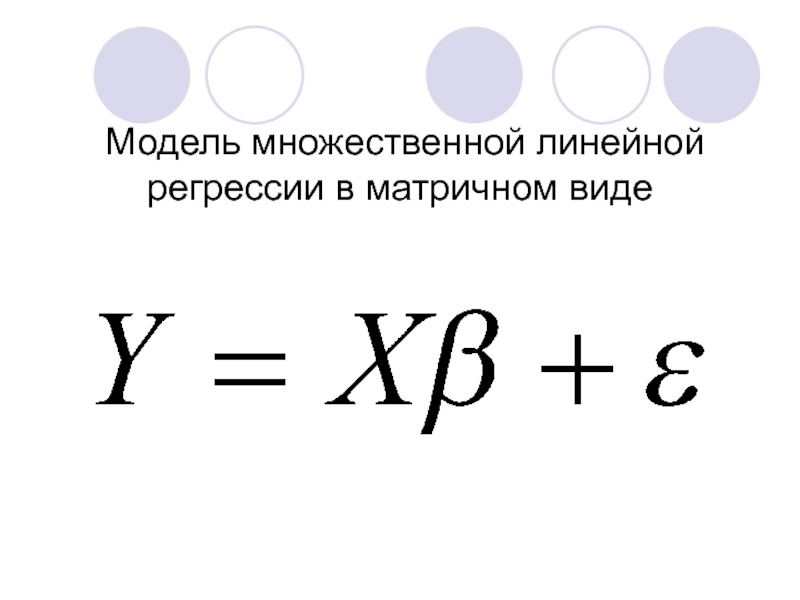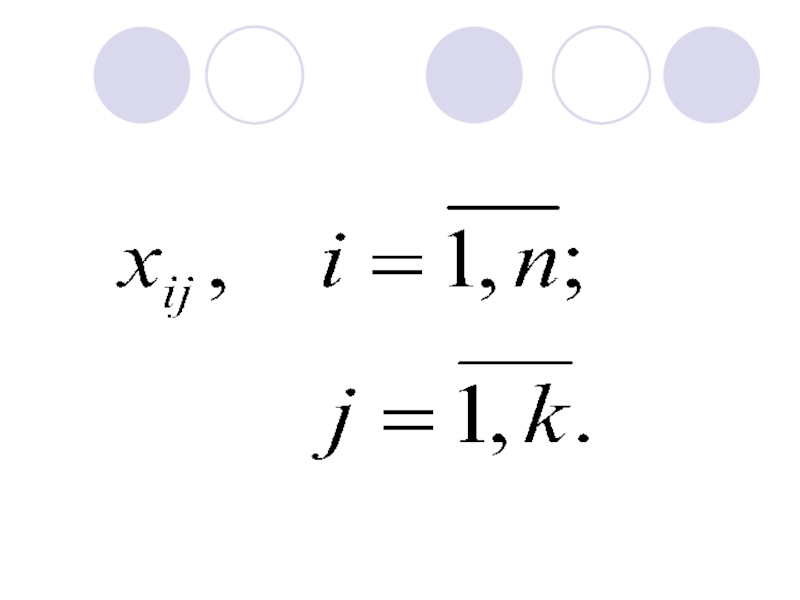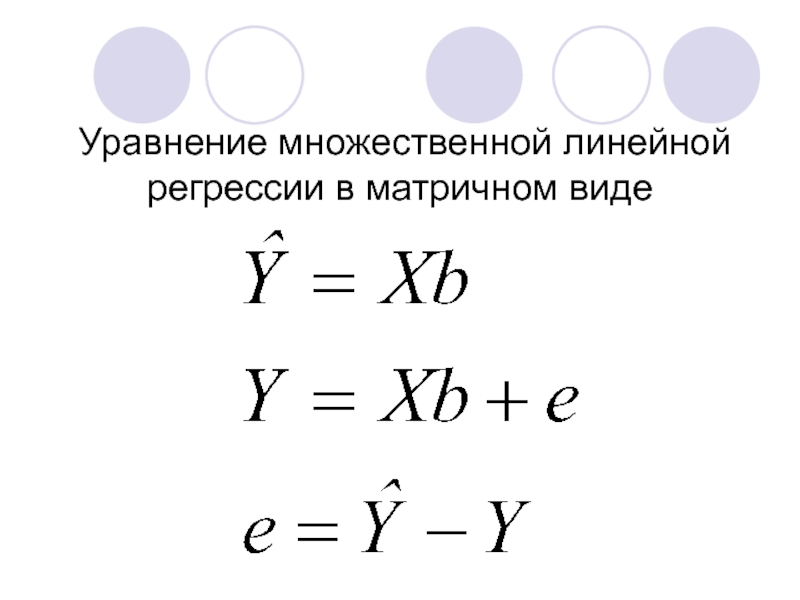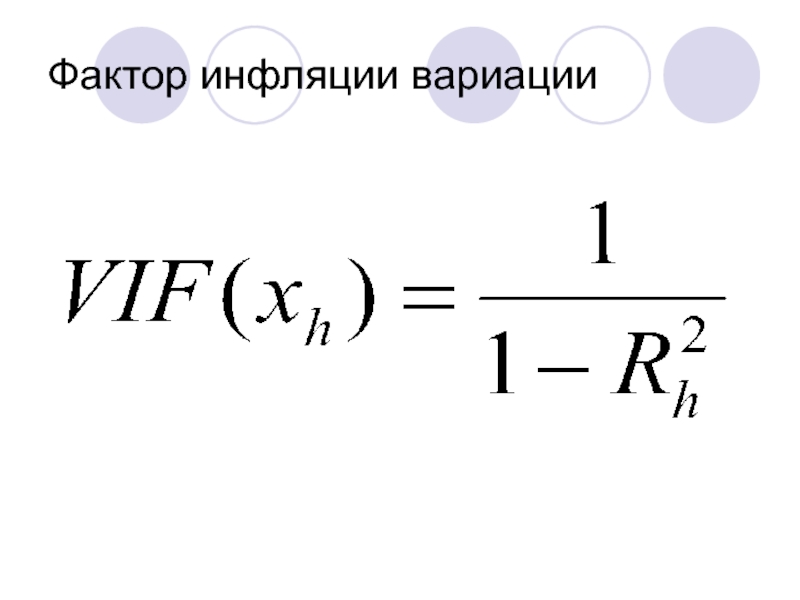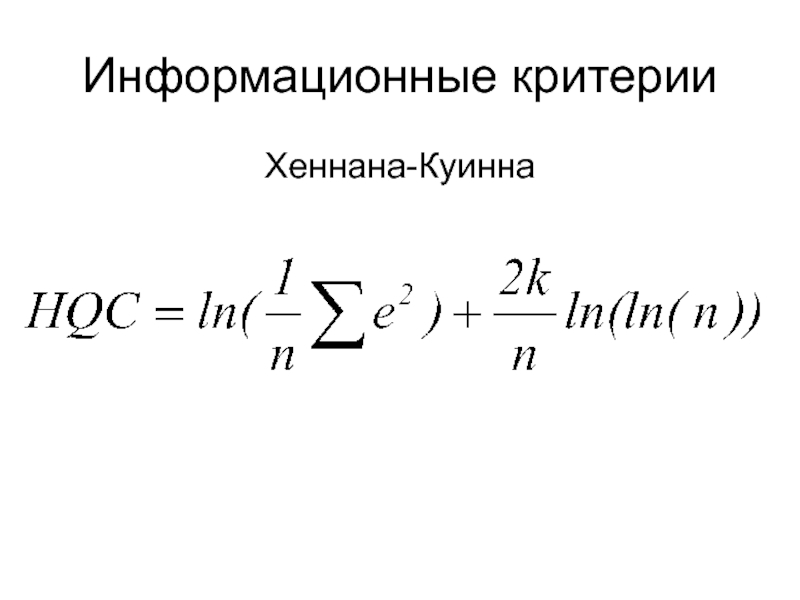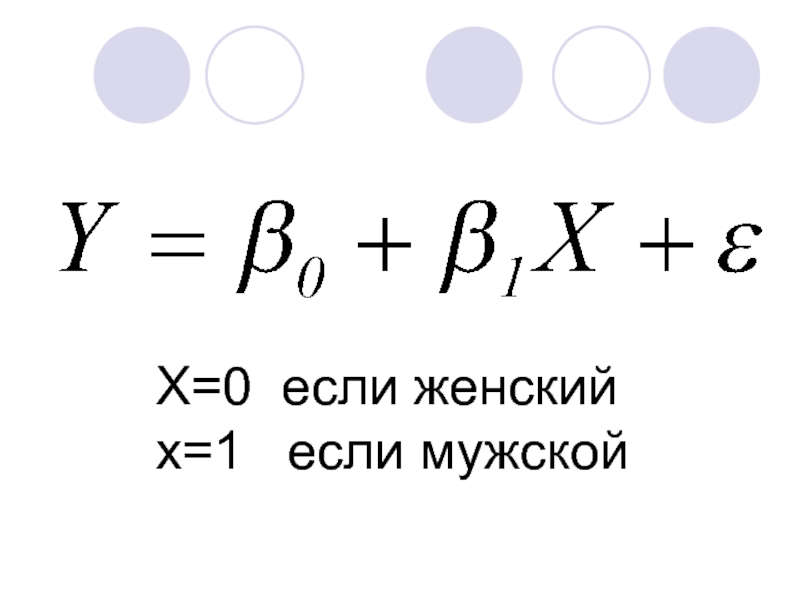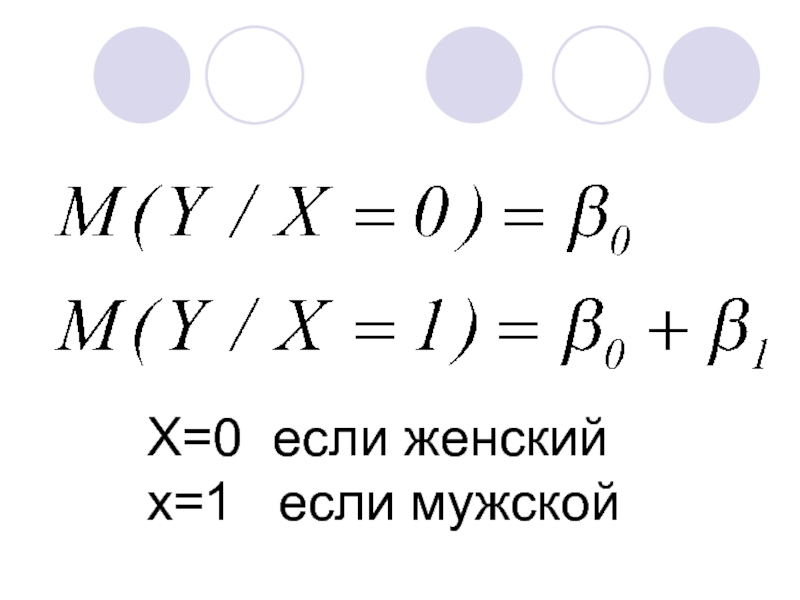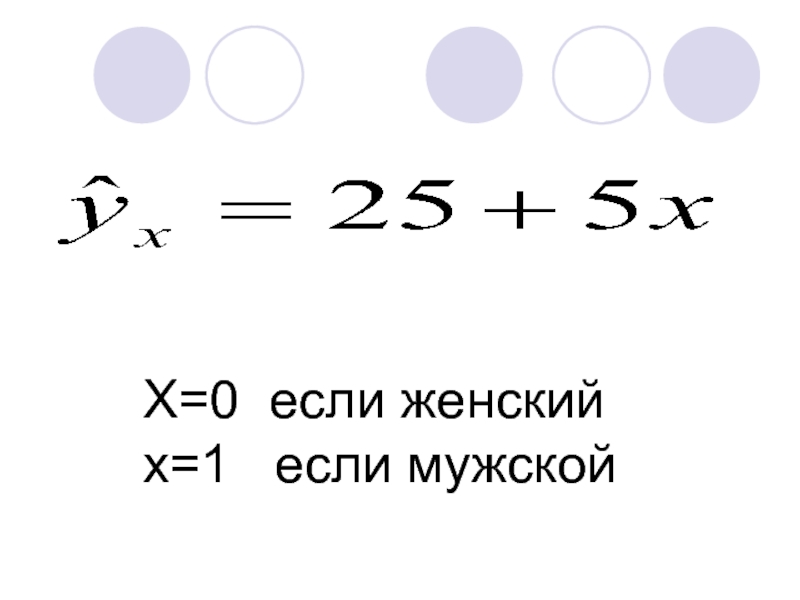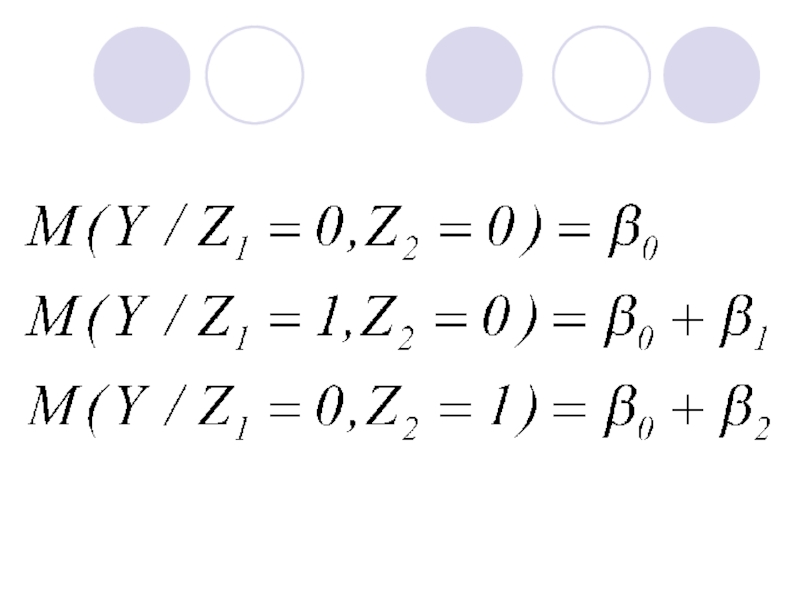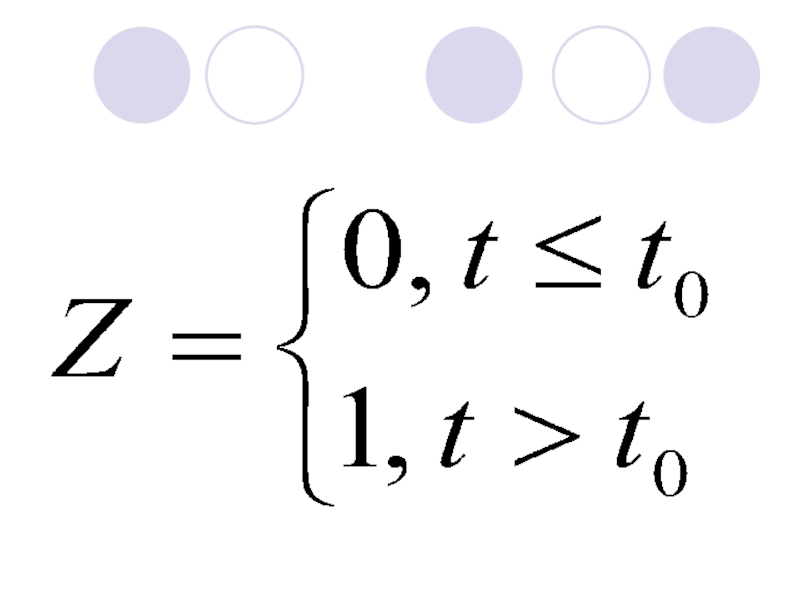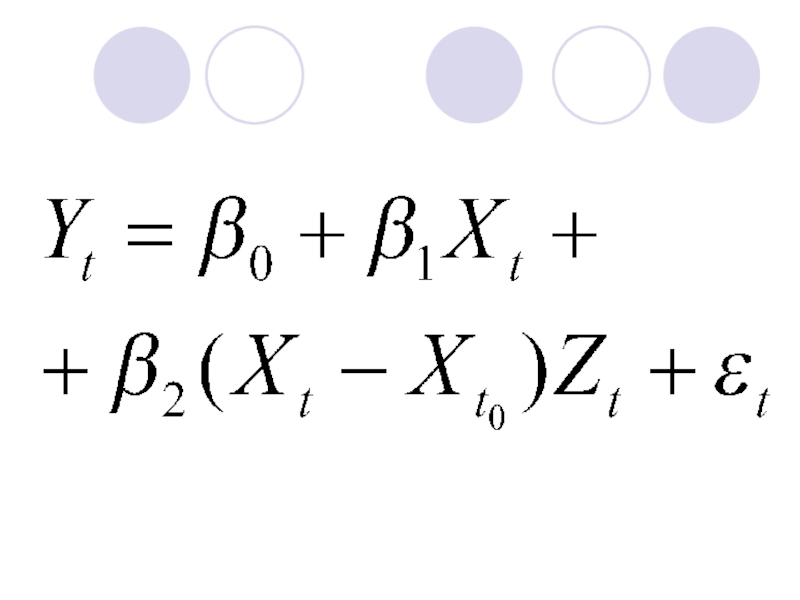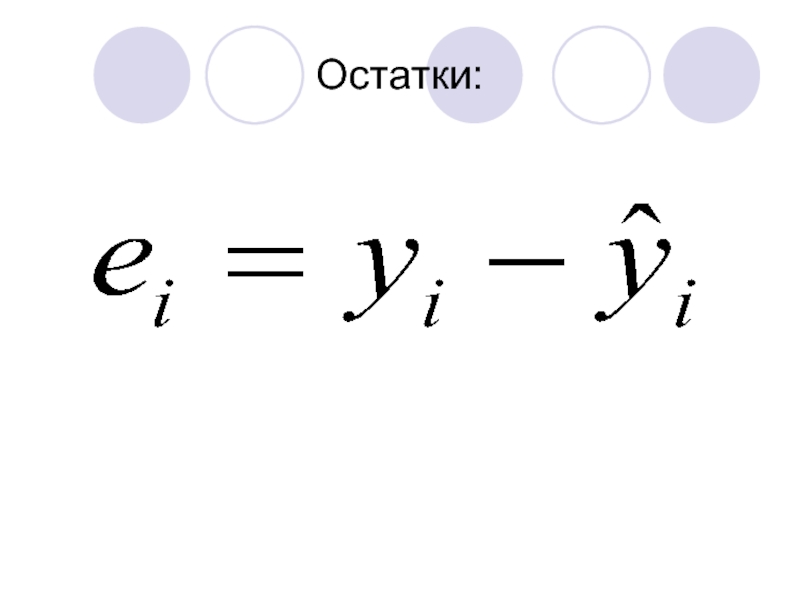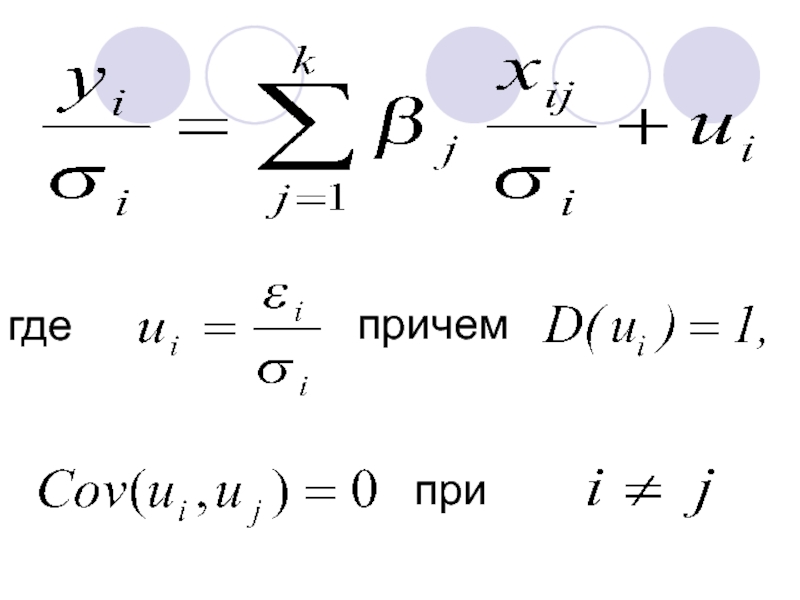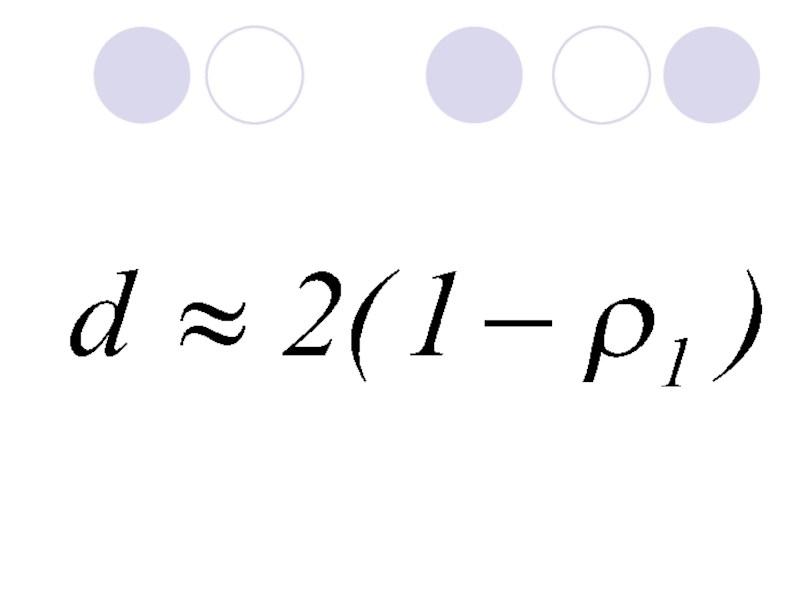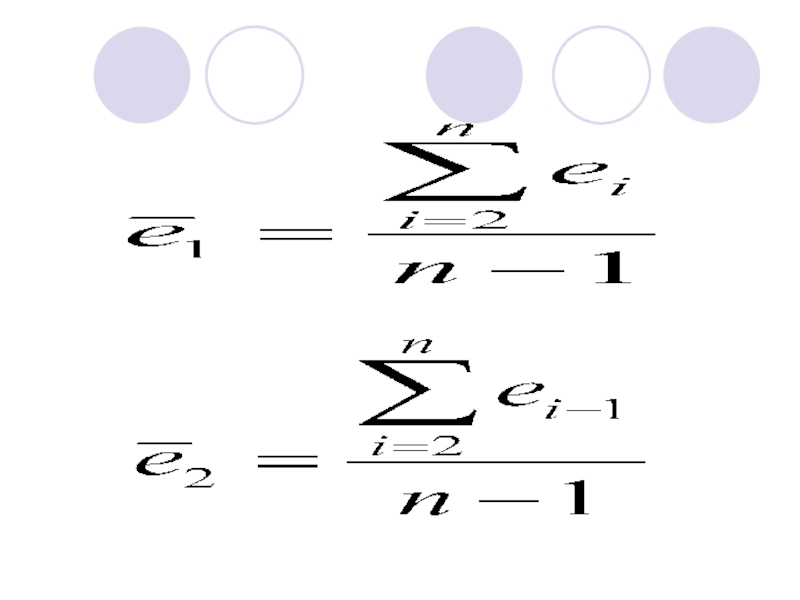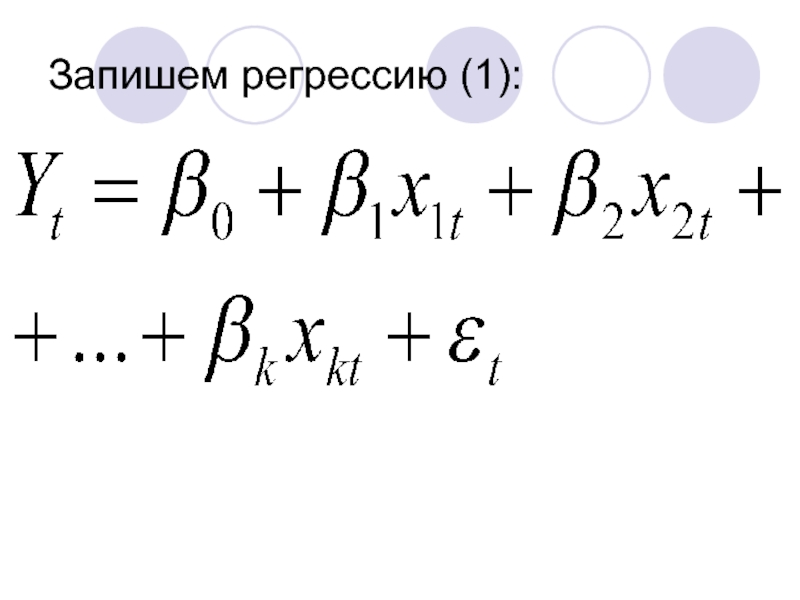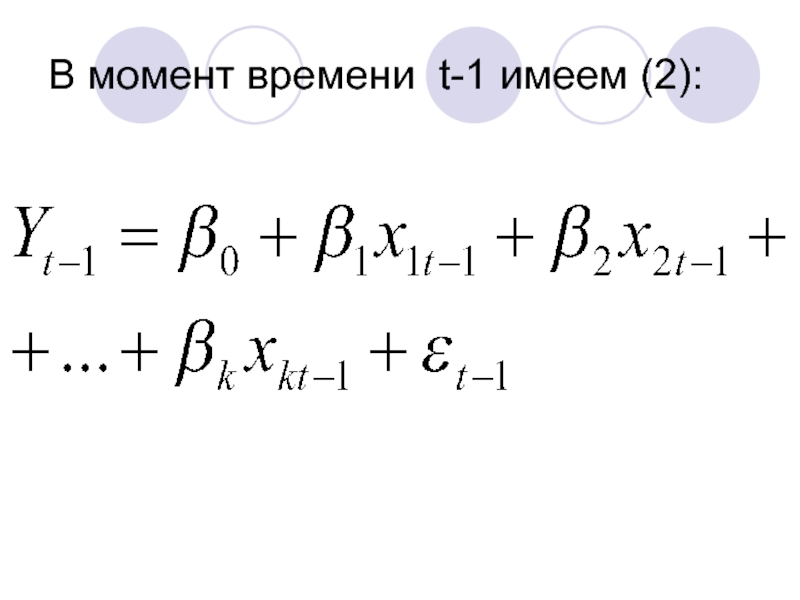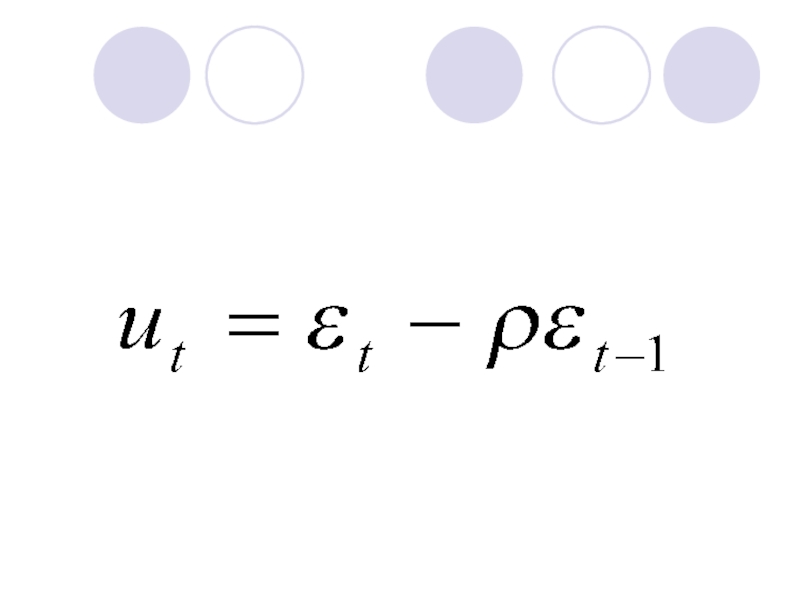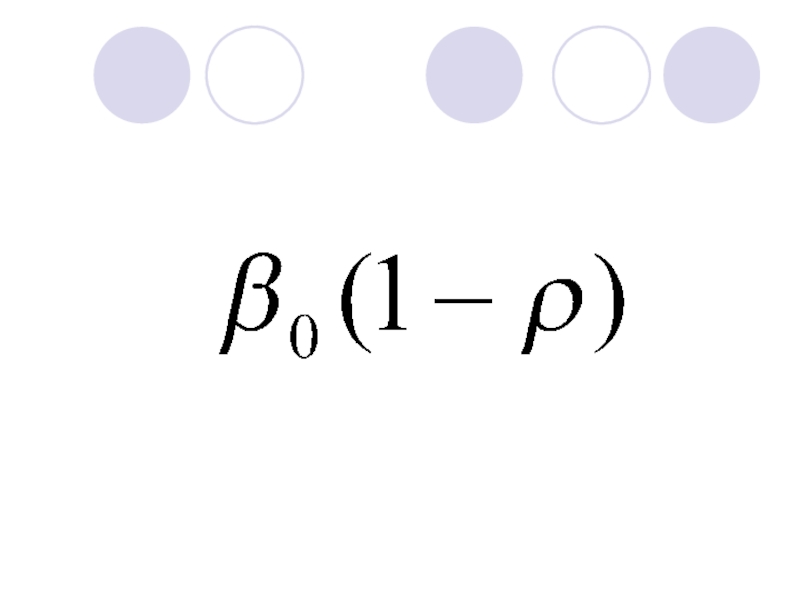- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Некоторые аспекты регрессионного анализа. Тема 4 презентация
Содержание
- 1. Некоторые аспекты регрессионного анализа. Тема 4
- 2. Вопросы: 4.1. Спецификация уравнения регрессии и ошибки
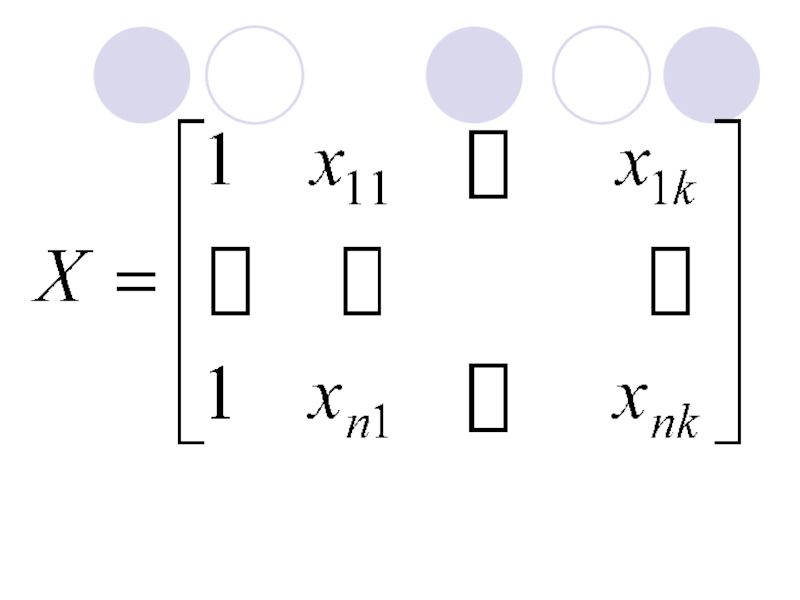
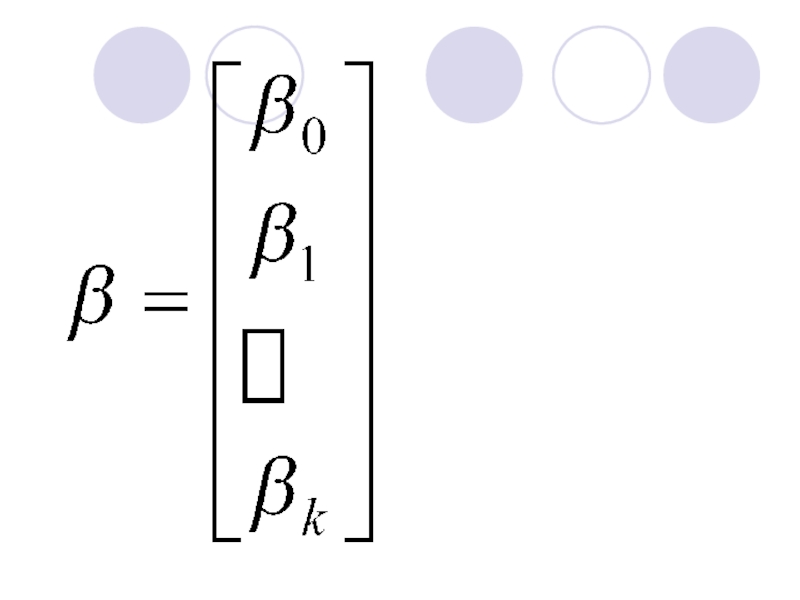
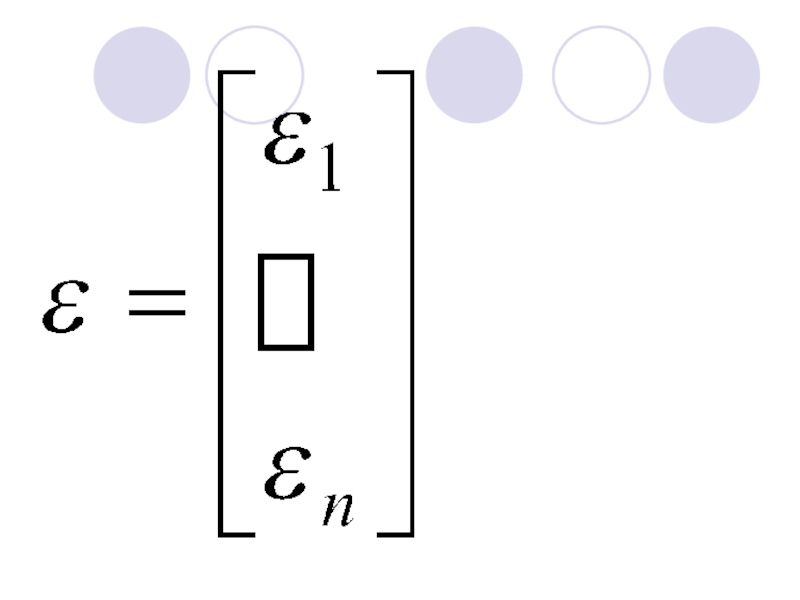
- 3. Модель множественной линейной регрессии в матричном виде
- 9. Уравнение множественной линейной регрессии в матричном виде
- 10. Метод наименьших квадратов
- 11. Условия теоремы Гаусса-Маркова 1.
- 12. Гомоскедастичность Гетероскедастичность
- 13. Условия теоремы Гаусса-Маркова
- 14. Условия теоремы Гаусса-Маркова
- 15. Мультиколлинеарность Способы выявления и устранения
- 16. Признаки наличия мультиколлинеарности 1. Небольшое изменение
- 17. Признаки наличия мультиколлинеарности 2. Стандартные ошибки
- 18. Признаки наличия мультиколлинеарности 3. Значения коэффициентов
- 19. Способы выявления мультиколлинеарности: 1. Вычисление матрицы
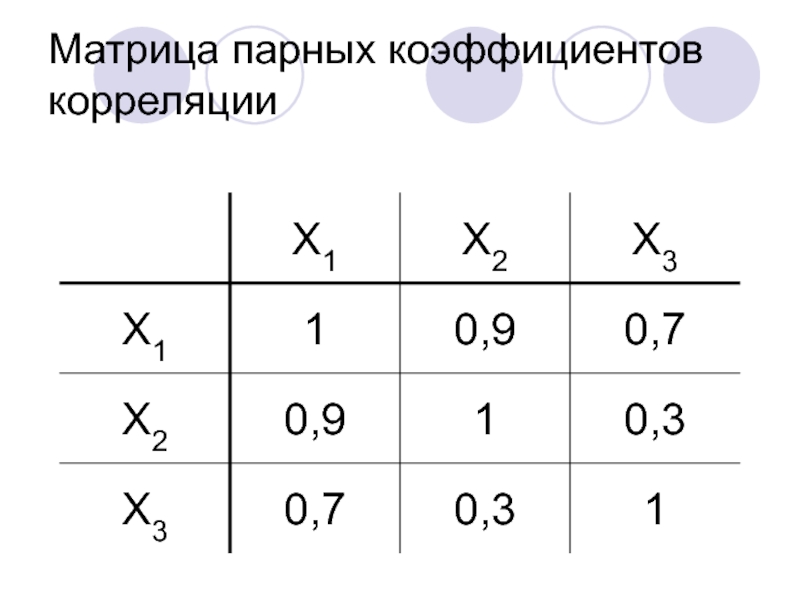
- 20. Матрица парных коэффициентов корреляции
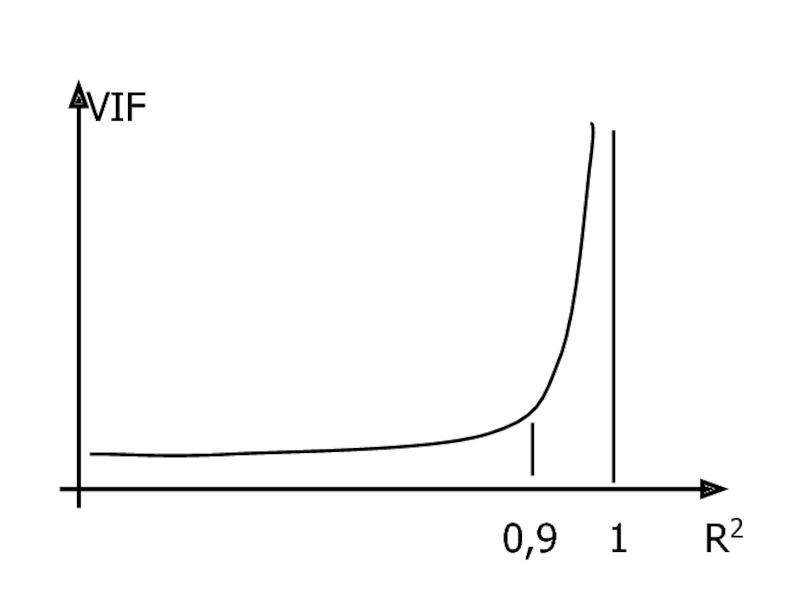
- 21. Фактор инфляции вариации
- 23. Методы устранения мультиколлинеарности: 1. Удаление коллинеарных переменных.
- 24. Случай 1. Исключены существенные переменные.
- 25. Случай 2. Включены несущественные переменные.
- 26. Информационные критерии Акаике и Шварца
- 27. Информационные критерии Хеннана-Куинна
- 28. Фиктивные переменные в регрессионных моделях dummy
- 29. X=0 если женский x=1 если мужской
- 30. X=0 если женский x=1 если мужской
- 31. X=0 если женский x=1 если мужской
- 34. неправильно
- 35. правильно
- 37. Фиктивные переменные позволяют строить и оценивать так
- 38. Пусть в момент времени tо произошли некие
- 41. Регрессионная линия (рис) имеет коэффициент наклона β1
- 42. Тестируя стандартную гипотезу β2=0 мы
- 44. ГЕТЕРОСКЕДАСТИЧНОСТЬ ОСТАТКОВ
- 45. Гомоскедастичность
- 46. Гетероскедастичность
- 47. Последствия гетероскедастичности Основное последствие гетероскедастичности заключается в
- 48. Способы обнаружения гетероскедастичности Графики Тесты
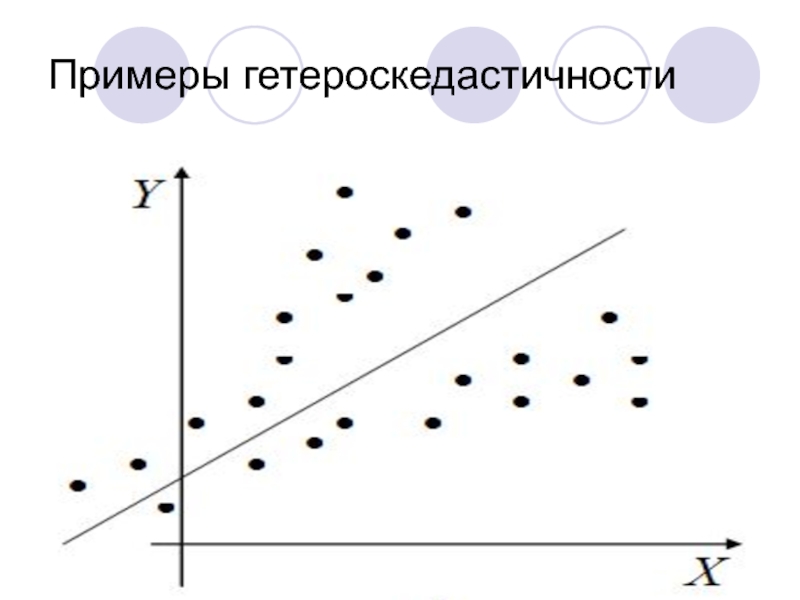
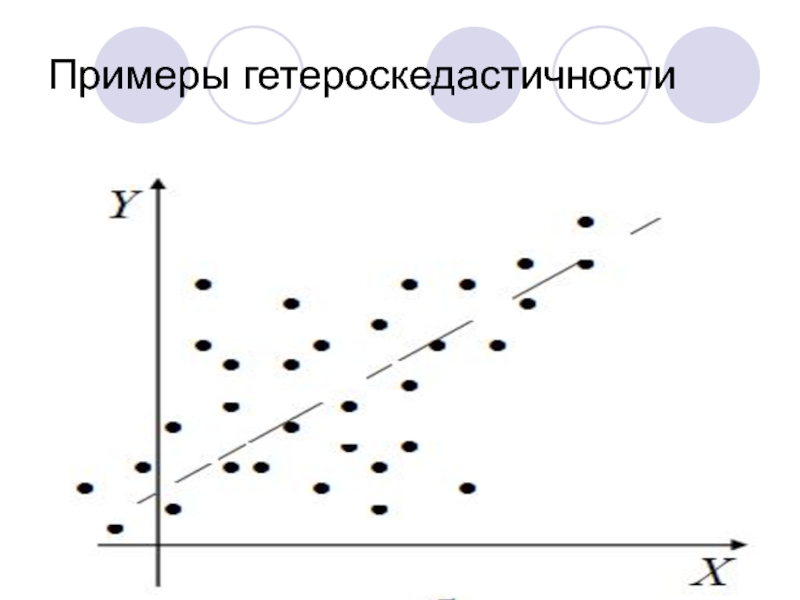
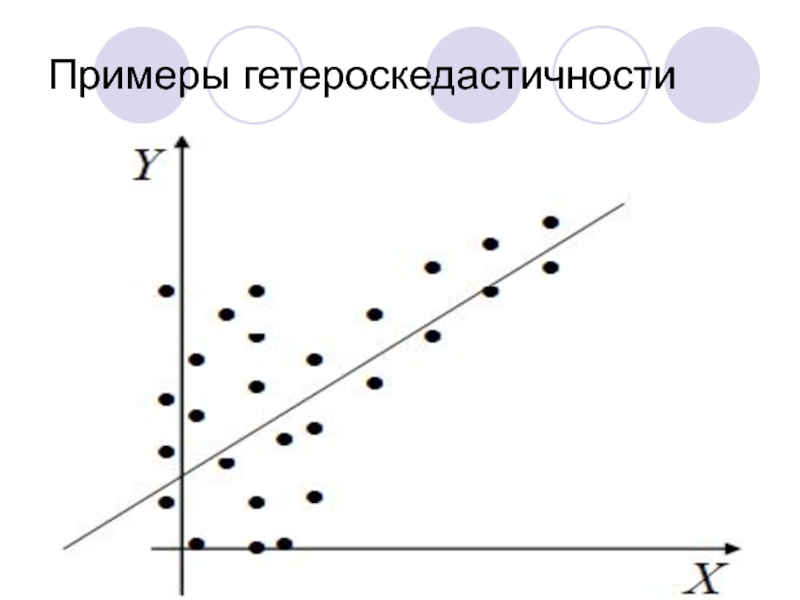
- 49. Примеры гетероскедастичности
- 50. Примеры гетероскедастичности
- 51. Примеры гетероскедастичности
- 52. Тесты на гетероскедастичность 1. Бартлетта 2. Голдфелда-Квандта 3. Уайта 4. Бреуша-Пагана 5. Глейзера
- 53. Остатки:
- 54. Вне зависимости от используемых тестов необходимо сформулировать
- 55. Тест Голдфелда-Куандта. 1. Упорядочить наблюдения по
- 56. Тест Голдфелда-Куандта. 2. Опустить v наблюдений,
- 57. Тест Голдфелда-Куандта. 3. Оценить отдельно обыкновенным
- 58. Тест Голдфелда-Куандта. 4. Найти SSE1 и
- 59. Тест Голдфелда-Куандта. 6. Найти Fкр. по
- 60. Если Fнабл.>Fкр., то нулевая гипотеза отклоняется
- 61. Тест Уайта. 1. Оцениваем параметры исходной модели, получаем уравнение регрессии
- 62. Тест Уайта. 2. Находим остатки
- 63. Тест Уайта. 4. Строим вспомогательную регрессию,
- 64. Тест Уайта. Например, для двухфакторной модели
- 65. Тест Уайта. 5. Оцениваем вспомогательную регрессию
- 66. Тест Уайта. 7. По таблице распределения
- 67. Тест Уайта. 8. Сравниваем наблюдаемое
- 68. Тест Уайта. Если
- 69. Тест Уайта (упрощенный) Отличается от классического
- 70. Тест Уайта (упрощенный). Тогда вспомогательная регрессия будет иметь вид:
- 71. Тест Уайта (упрощенный). А число степеней свободы k = 2-1=1
- 72. Критерий Бартлетта.
- 73. Критерий Бартлетта.
- 75. Обобщенный МНК Отличается от обычного МНК
- 76. Обобщенный МНК Или Обычный МНК:
- 77. Обобщенный МНК Если есть только гетероскедастичность,
- 78. Обобщенный МНК Критерий минимизации суммы квадратов
- 79. Обобщенный МНК Соответственно усложняется вид системы
- 80. Обобщенный МНК Соответственно усложняется вид системы
- 81. Обобщенный МНК
- 82. Обобщенный МНК Оценки МНК
- 83. Обобщенный МНК Для
- 84. Взвешенный МНК Предположим, что нам известны
- 85. Исходная модель
- 86. где причем при
- 87. Взвешенный МНК Для получения оценок неизвестных
- 88. Взвешенный МНК Принимая различные гипотезы относительно
- 89. Взвешенный МНК Если дисперсия случайного члена
- 90. Взвешенный МНК Если предположить, что дисперсия
- 91. Существуют также и другие методы коррекции модели
- 92. Стандартные ошибки в форме Ньюи-Веста. Пусть
- 93. Автокорреляция в остатках
- 94. пространственные данные – cross-sectional data; временные ряды данных – time-series data
- 95. Условие отсутствия автокорреляции
- 96. Причины автокорреляции Стохастические зависимости между значениями случайных
- 97. Последствия автокорреляции: 1. Выборочные дисперсии полученных оценок коэффициентов
- 98. Стандартные ошибки коэффициентов будут оценены неправильно, т.е.
- 99. Можно рассматривать так называемую корреляцию сериями (автокорреляцию),
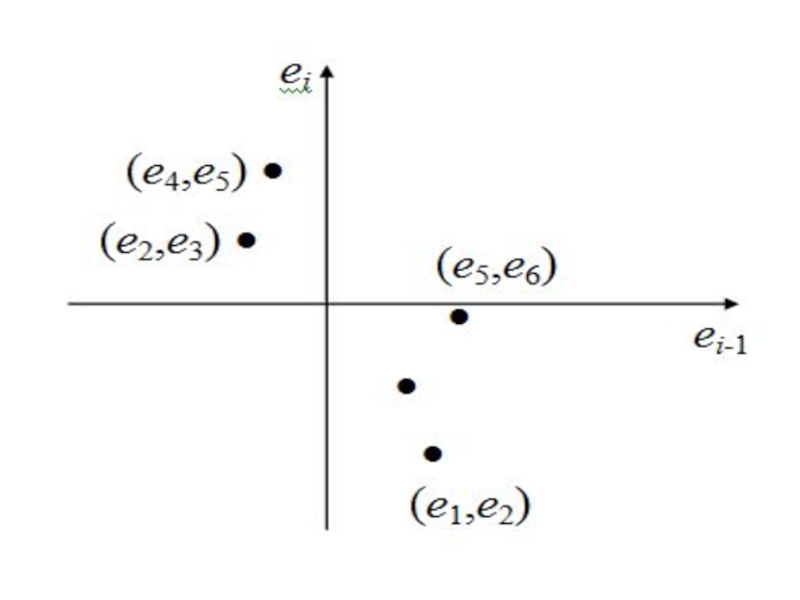
- 100. система координат (ei; ei-s)
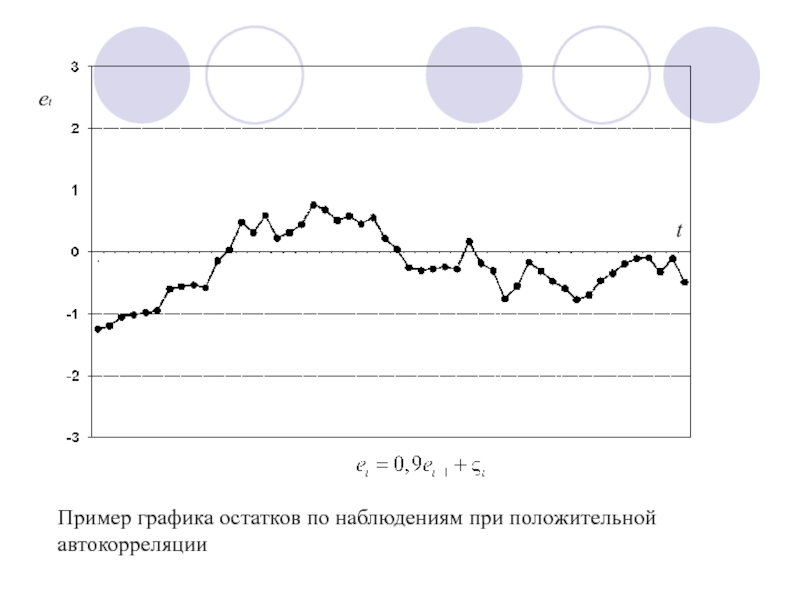
- 103. et t Пример графика остатков по наблюдениям при положительной автокорреляции
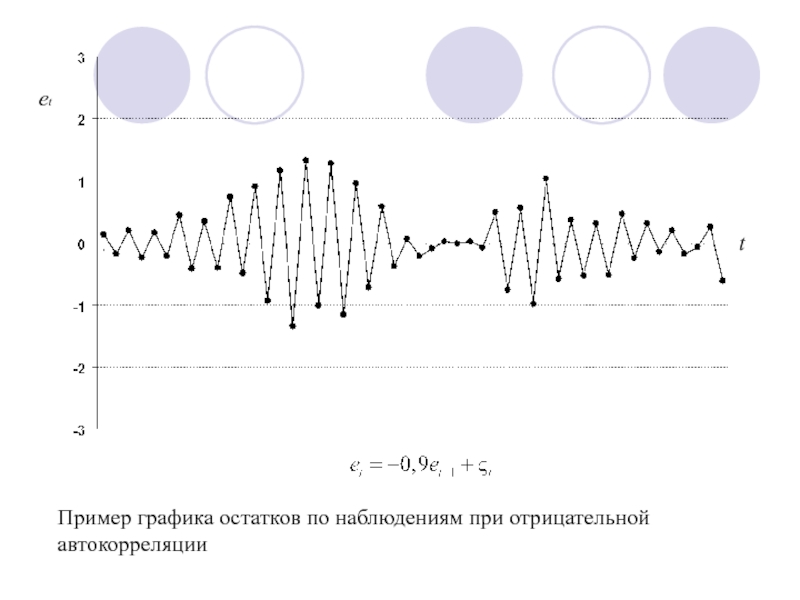
- 104. Пример графика остатков по наблюдениям при отрицательной автокорреляции et t
- 106. Тестирование на наличие автокорреляции. Для проверки
- 107. Критерий Дарбина-Уотсона.
- 108. Тестирование на наличие автокорреляции. Критерий
- 110. Коэффициент автокорреляции первого порядка
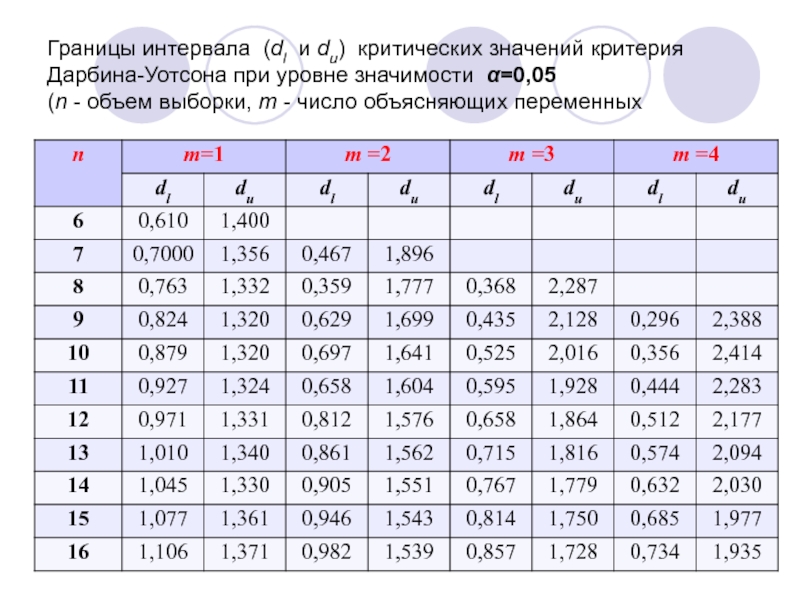
- 112. По таблице Дарбина-Уотсона определяются две критические точки: верхняя dU и нижняя dL.
- 113. Границы интервала (dl и du) критических значений
- 114. 2 4 0 dL dU
- 116. Методы устранения автокорреляции Кохрейна-Оркатта Хилдрета-Лу Дарбина
- 117. Запишем регрессию (1):
- 118. В момент времени t-1 имеем (2):
- 119. Умножим уравнение (2) на коэффициент автокорреляции ρ:
- 120. Вычтем уравнение (2) из уравнения (1)
- 124. Предположим, что остатки ui удовлетворяют следующему уравнению:
- 125. Оценивание регрессии при наличии автокорреляции. Метод 1.
- 126. Метод 3. Итеративная процедура Кохрейна-Оркатта. а) Оценивается регрессия
- 127. Метод 4. Метод Хилдрета-Лу. Основан на
- 128. Метод 5. Метод Дарбина. Получаем оценку
Слайд 2Вопросы:
4.1. Спецификация уравнения регрессии и ошибки спецификации.
4.2. Мультиколлинеарность: способы выявления и
4.3. Фиктивные переменные в регрессионных моделях.
4.4. Гетероскедастичность
4.5. Автокорреляция
Слайд 16Признаки наличия мультиколлинеарности
1. Небольшое изменение
исходных данных сильно
изменяет значения оценок
коэффициентов
Слайд 17Признаки наличия мультиколлинеарности
2. Стандартные ошибки
коэффициентов очень
велики
модель в целом
статистически значима
Слайд 18Признаки наличия мультиколлинеарности
3. Значения коэффициентов
неправильны с точки
теории
Слайд 19Способы выявления мультиколлинеарности:
1. Вычисление матрицы парных коэффициентов корреляции для всех
2. Расчет фактора инфляции вариации VIF (variance inflation factor).
Слайд 23Методы устранения мультиколлинеарности:
1. Удаление коллинеарных переменных.
2. Исправление выборки (проверка ее репрезентативности).
3.
4. Использование в модели регрессии эффекта взаимодействия факторов, например в виде их произведения.
Слайд 37Фиктивные переменные позволяют строить и оценивать так называемые кусочно-линейные модели, которые
Пусть х и у представлены в виде временных рядов.
xt – размер ОПФ в период времени t,
уt – объем выпуска продукции в период времени t.
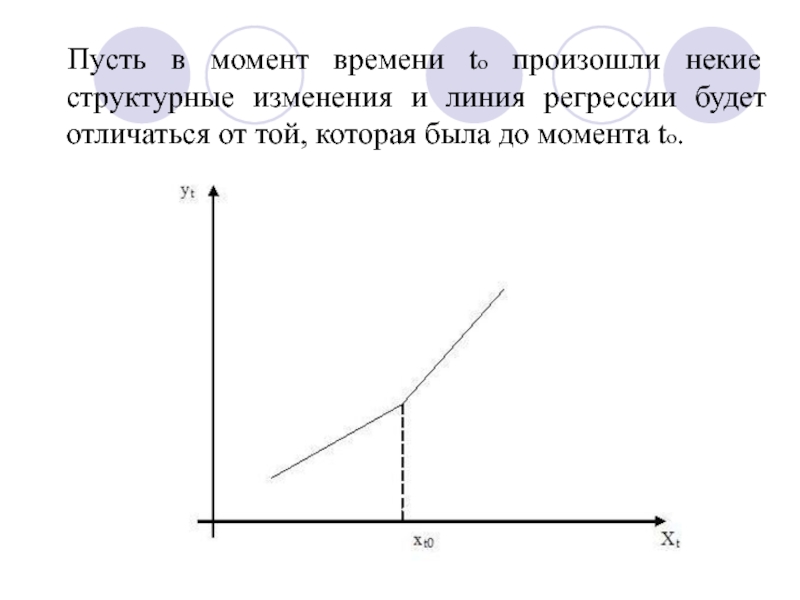
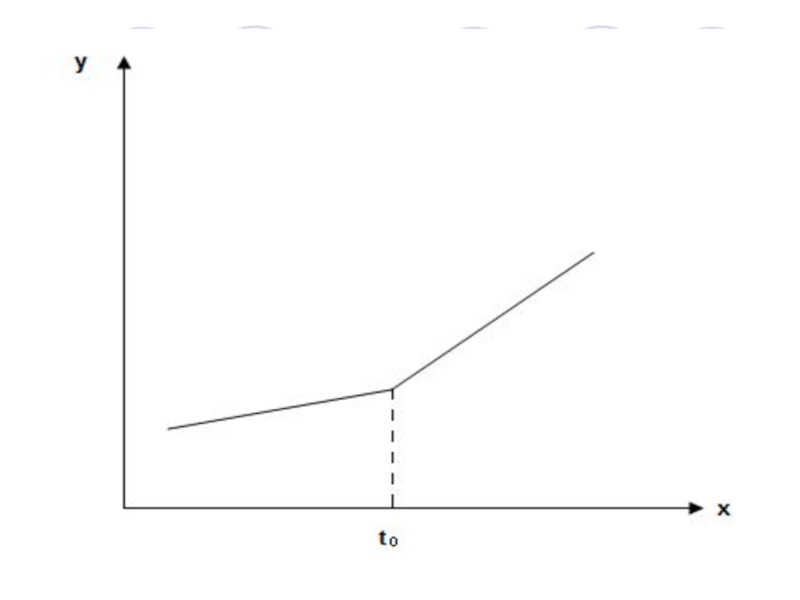
Слайд 38Пусть в момент времени tо произошли некие структурные изменения и линия
Слайд 41Регрессионная линия (рис) имеет коэффициент наклона β1 для t ≤ to
Слайд 42
Тестируя стандартную гипотезу β2=0 мы проверяем предположение о том, что фактически
Слайд 47Последствия гетероскедастичности
Основное последствие гетероскедастичности заключается в получении неэффективных оценок параметров модели
Слайд 52Тесты на гетероскедастичность
1. Бартлетта
2. Голдфелда-Квандта
3. Уайта
4. Бреуша-Пагана
5. Глейзера
Слайд 54Вне зависимости от используемых тестов необходимо сформулировать гипотезы:
при i=j
остатки гомоскедастичны
при i=j
остатки гетероскедастичны
Слайд 55Тест Голдфелда-Куандта.
1. Упорядочить наблюдения по убыванию той независимой переменной, относительно
Слайд 56Тест Голдфелда-Куандта.
2. Опустить v наблюдений, оказавшихся в центре (v должно
Слайд 57Тест Голдфелда-Куандта.
3. Оценить отдельно обыкновенным МНК регрессии на первых (n−v)/2
Слайд 58Тест Голдфелда-Куандта.
4. Найти SSE1 и SSE2 – суммы квадратов остатков
5. Найти Fнабл.
Слайд 59Тест Голдфелда-Куандта.
6. Найти Fкр. по таблице распределения Фишера по уровню
k1= k2= (n-v-2m)/2 .
Слайд 60 Если Fнабл.>Fкр., то нулевая гипотеза отклоняется в пользу альтернативной о
Иначе оснований отклонять нулевую гипотезу о гомоскедастичности остатков нет.
Слайд 63Тест Уайта.
4. Строим вспомогательную регрессию, в которой в качестве зависимой
Слайд 65Тест Уайта.
5. Оцениваем вспомогательную регрессию и находим R2
вспомогательной регрессии.
6. Вычисляем наблюдаемое значение
Слайд 66Тест Уайта.
7. По таблице распределения Пирсона по уровню значимости α
m – число параметров во вспомогательной регрессии.
Слайд 68Тест Уайта.
Если
нельзя отклонить нулевую гипотезу об отсутствии гетероскедастичности.
Если ,
нулевая гипотеза отклоняется в пользу конкурирующей о наличии гетероскедастичности.
Слайд 69Тест Уайта (упрощенный)
Отличается от классического вспомогательной регрессией, в которой в
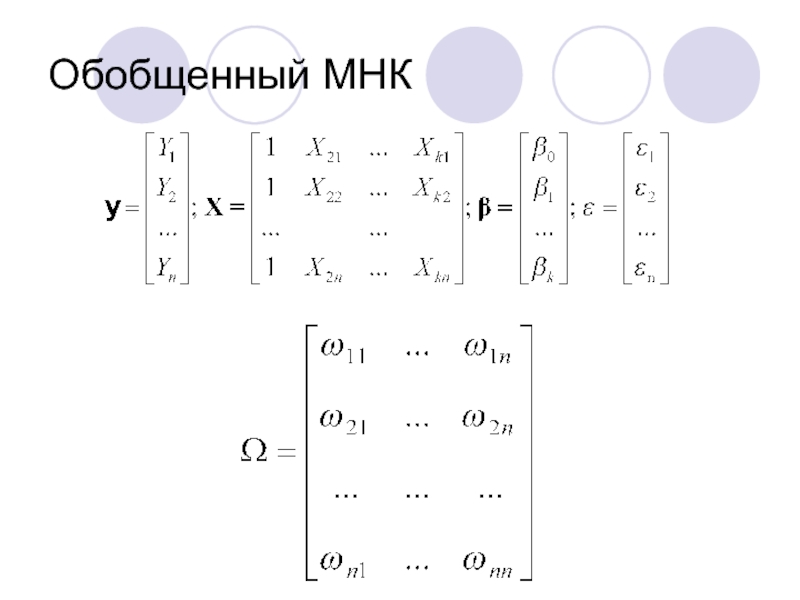
Слайд 75Обобщенный МНК
Отличается от обычного МНК в изменении предположений о поведении случайной
Обычный МНК:
Обобщенный МНК:
Слайд 78Обобщенный МНК
Критерий минимизации суммы квадратов ошибок МНК заменяется на другой –
Слайд 79Обобщенный МНК
Соответственно усложняется вид системы уравнений для определения оценок коэффициентов. ОМНК
Слайд 80Обобщенный МНК
Соответственно усложняется вид системы уравнений для определения оценок коэффициентов. ОМНК
Слайд 83Обобщенный МНК
Для применения ОМНК необходимо знать элементы матрицы Ω, что на
Слайд 84Взвешенный МНК
Предположим, что нам известны значения величин
Тогда исходную модель разделим на σi:
Слайд 87Взвешенный МНК
Для получения оценок неизвестных дисперсий будем предполагать, что они пропорциональны
где σ2 – некоторая константа.
Слайд 88Взвешенный МНК
Принимая различные гипотезы относительно характера гетероскедастичности, будем иметь соответствующие значения
Если дисперсия случайного члена пропорциональна квадрату регрессора X, так что
то
Слайд 90Взвешенный МНК
Если предположить, что дисперсия случайного члена пропорциональна
Слайд 91Существуют также и другие методы коррекции модели на гетероскедастичность, в частности,
Известны способы коррекции стандартных ошибок Уайта и Ньюи-Веста.
Стандартные ошибки в форме Уайта.
Рассмотрим матрицу XTΩX. Имеем ij-й элемент матрицы получается по
формуле (XTΩX)ij = . Обозначим как векторы-строки
размерности 1×k матрицы регрессоров X. Тогда XTΩX = . Уайт
предложил использовать в качестве состоятельной оценки матрицы ковариаций оценок коэффициентов величину:
Стандартные отклонения, рассчитанные по последней формуле, являются состоятельными стандартными ошибками при наличии гетероскедастичности.
Слайд 92Стандартные ошибки в форме Ньюи-Веста.
Пусть в матрице ковариаций Ω ненулевые
Ньюи и Вест показали, что оценка:
является состоятельной оценкой матрицы ковариаций оценок коэффициентов регрессии.
Веса wj выбираются либо по Бартлетту: ,
либо по Парзену:
Стандартные ошибки, рассчитанные по Ньюи и Весту, являются состоятельными стандартными ошибками при наличии гетероскедастичности и автокорреляции остатков.
Слайд 96Причины автокорреляции
Стохастические зависимости между значениями случайных ошибок – автокорреляция ошибок.
Ее
влияние некоторых случайных факторов или опущенных в уравнении регрессии важных объясняющих переменных, которое не является однократным, а действует в разные периоды времени;
случайный член может содержать составляющую, учитывающую ошибку измерения объясняющей переменной.
Слайд 97Последствия автокорреляции:
1. Выборочные дисперсии полученных оценок коэффициентов будут больше по сравнению с
2. Стандартные ошибки коэффициентов будут оценены неправильно, чаще всего занижены, иногда настолько, что нет возможности воспользоваться для проверки гипотез соответствующими точными критериями – мы будем чаще отвергать гипотезу о незначимости регрессии, чем это следовало бы делать в действительности.
Автокорреляция означает нарушение условия Гаусса-Маркова, которое принимает вид:
и матрица ковариаций:
Слайд 98Стандартные ошибки коэффициентов будут оценены неправильно, т.е. оценки коэффициентов будут неэффективны.
Выводы о значимости оценок коэффициентов будут некорректны.
Последствия автокорреляции:
Слайд 99Можно рассматривать так называемую корреляцию сериями (автокорреляцию), когда зависимость между ошибками,
Например, для s=1 показаны отрицательная (слева) и положительная (справа) автокорреляция остатков. В экономических исследованиях чаще всего встречается положительная автокорреляция.
Слайд 106Тестирование на наличие автокорреляции.
Для проверки гипотезы о существовании линейной автокорреляции первого
Слайд 108Тестирование на наличие автокорреляции.
Критерий Дарбина-Уотсона предназначен для моделей с детерминированными регрессорами
Для больших выборок
Автокорреляция отсутствует
Положительная автокорреляция
Отрицательная автокорреляция
Слайд 113Границы интервала (dl и du) критических значений критерия Дарбина-Уотсона при уровне
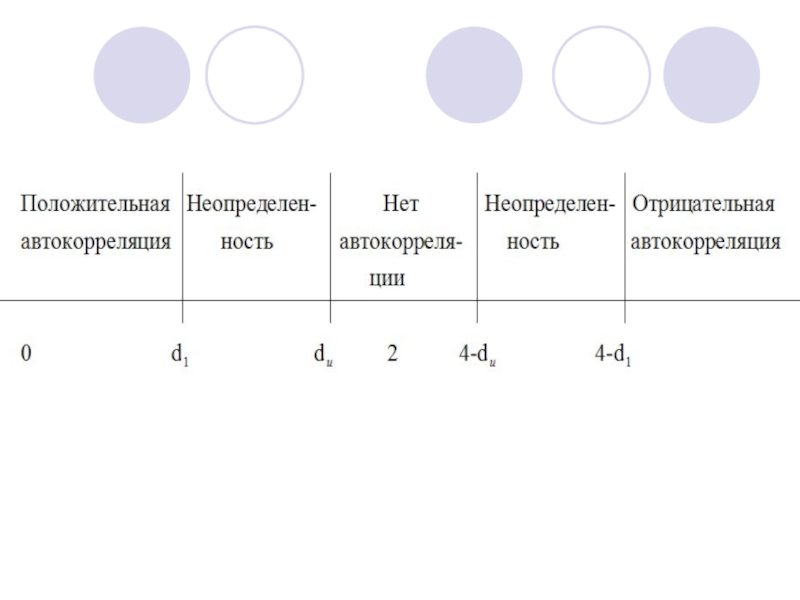
Слайд 114
2
4
0
dL
dU
dcrit
положительная
автокорреляция
отрицательная автокорреляция
нет автокорреляции
dcrit
Области статистических решений для критерия Дарбина-Уотсона
H0: ρ=0 (автокорреляции
H1: ρ≠0 (автокорреляция есть)
4-dL
4-dU
Слайд 124Предположим, что остатки ui удовлетворяют следующему уравнению:
ui=ρui-1+ςi, i=2,...,n,
представляющему собой авторегрессионную модель первого порядка, для которой выполнено |ρ|≤1, а ςi удовлетворяют условиям:
E(ςi)=0 и
Тогда несложно показать, что будет выполняться:
и матрица ковариаций
Слайд 125Оценивание регрессии при наличии автокорреляции.
Метод 1. Отказавшись от определения величины ρ
Однако даже грубая статистическая оценка будет более эффективной, поэтому другой способ определения ρ с помощью статистики Дарбина-Уотсона ρ≈1–0,5d.
Применяя затем непосредственно ОМНК, получим оценки коэффициентов.
Метод 2. Рассмотрим на примере парной регрессии:
(4.12)
причем и .
Ошибки в (4.12) не автокоррелированы и можно применять МНК.
Слайд 126Метод 3. Итеративная процедура Кохрейна-Оркатта.
а) Оценивается регрессия
б) Вычисляются остатки ei.
в) Оценивается регрессия ei=ρei-1+ςi, и коэффициент при ei-1 дает оценку ρ.
г) С учетом полученной оценки ρ уравнение
преобразовывается к виду (4.12), оценивание которого позволяет получить пересмотренные оценки коэффициентов β0 и β1.
д) Вычисляются остатки регрессии (4.12) и процесс выполняется снова, начиная с этапа в).
Итерации заканчиваются, когда абсолютные разности последовательных значений оценок коэффициентов β0, β1 и ρ будут меньше заданного числа (точности).
Подобная процедура оценивания порождает проблемы, касающиеся сходимости итерационного процесса и характера найденного минимума: локальный или глобальный
Слайд 127Метод 4. Метод Хилдрета-Лу.
Основан на тех же принципах, что и
Слайд 128Метод 5. Метод Дарбина.
Получаем оценку ρ как коэффициента при Yi-1
Вычисляем значения преобразованных переменных
и применяем к ним обыкновенный МНК. Получаем искомые оценки коэффициентов регрессии.