- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Умножение вектора на число презентация
Содержание
- 1. Умножение вектора на число
- 2. Прежде, чем ввести
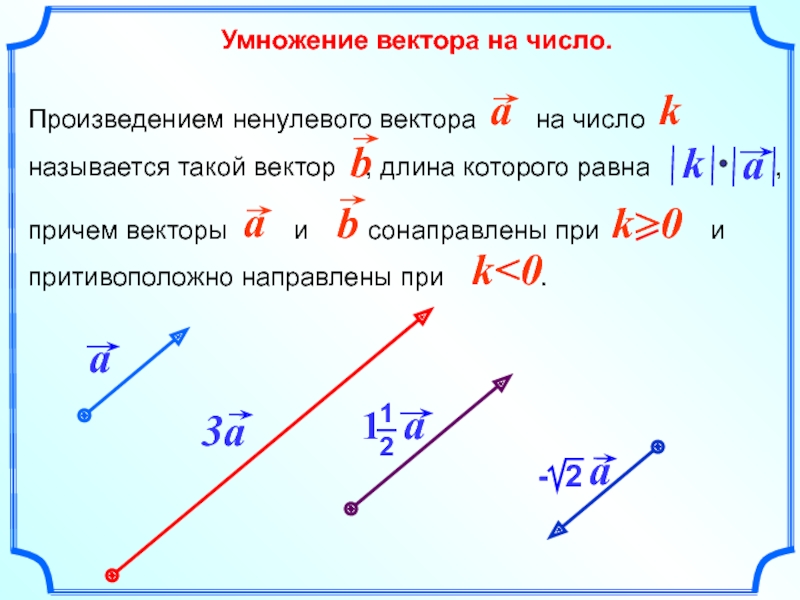
- 3. Умножение вектора на число.
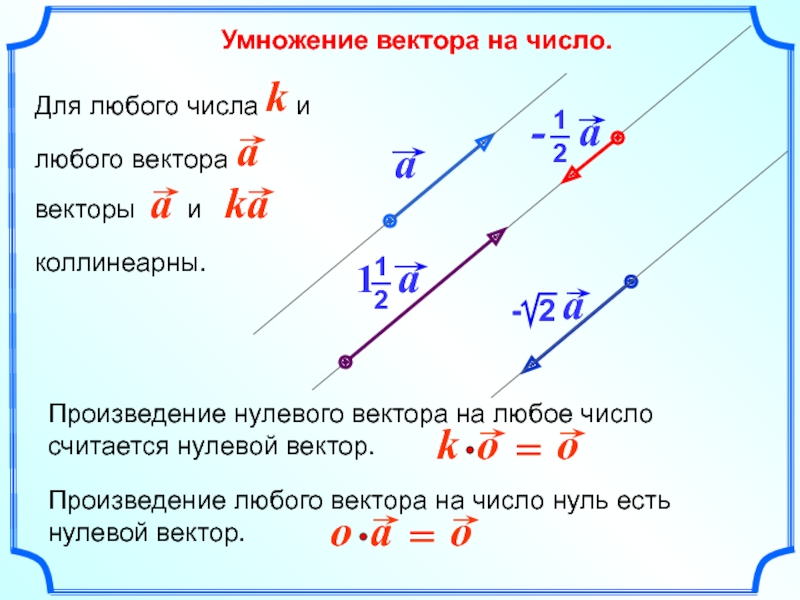
- 4. Умножение вектора на число.
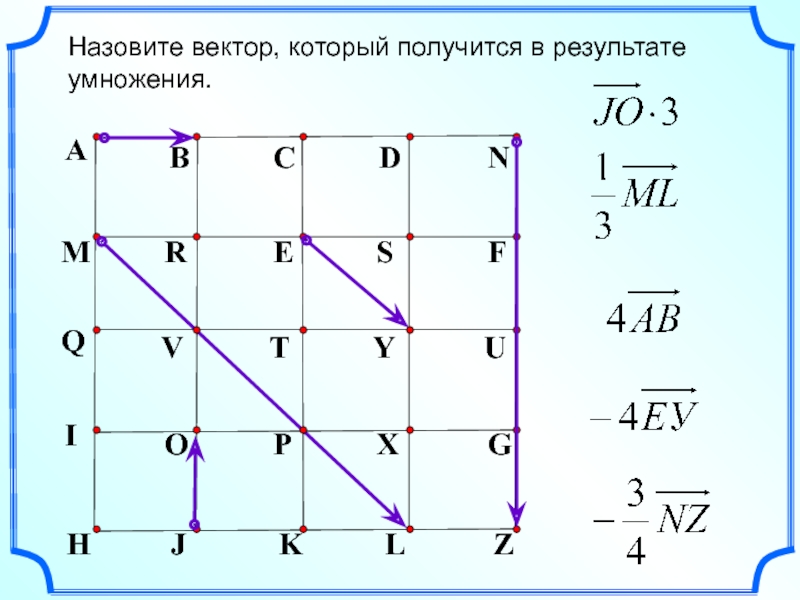
- 5. Умножение вектора на число. Произведение любого вектора
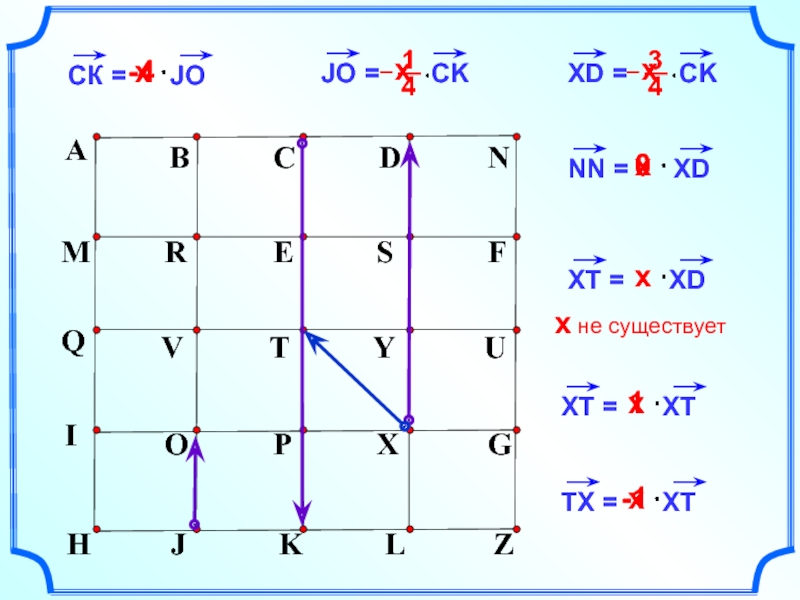
- 6. A
- 7. х -4 0 х A
- 8. 2 х 3 A
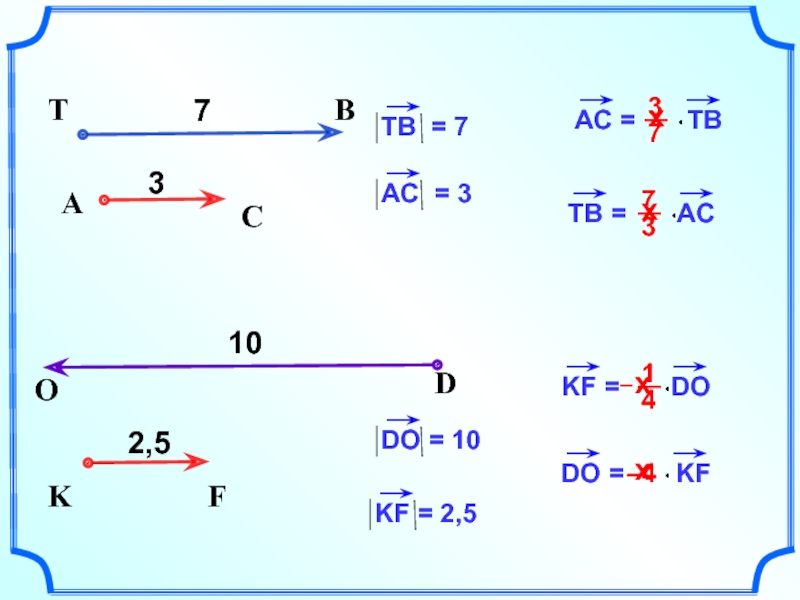
- 9. х –4 A C 7 T B х 3 х х
- 10. х 1,25 A C T B ТВ
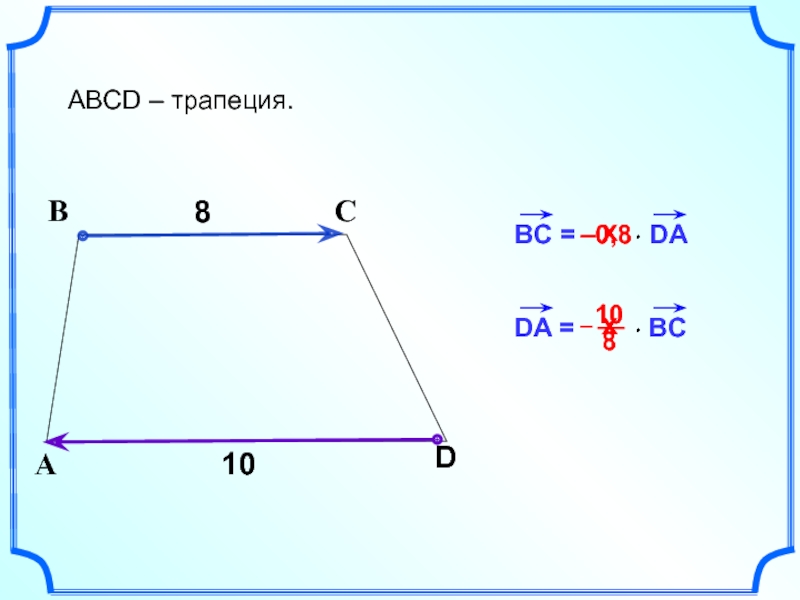
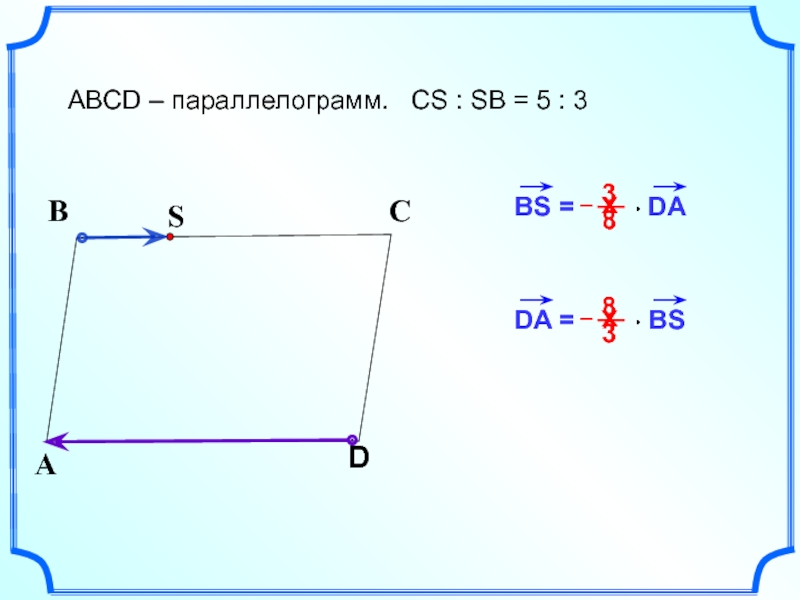
- 11. BC = DA
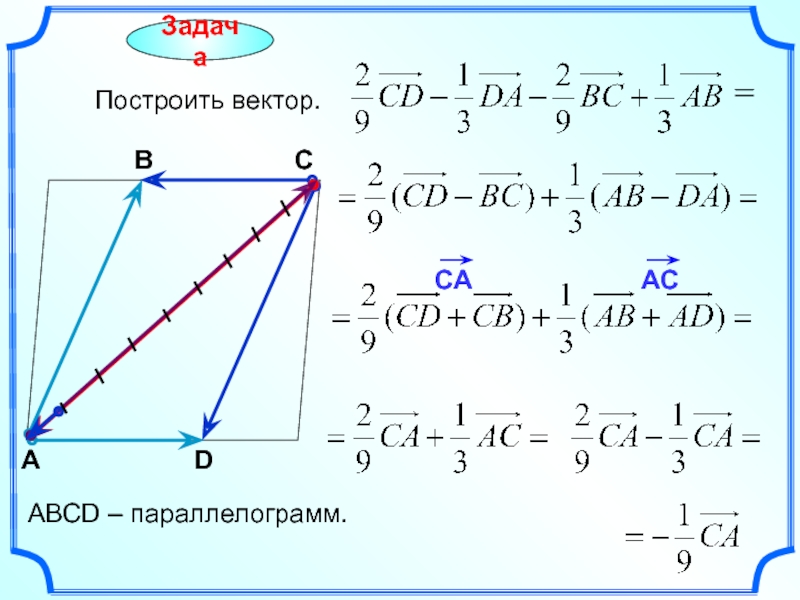
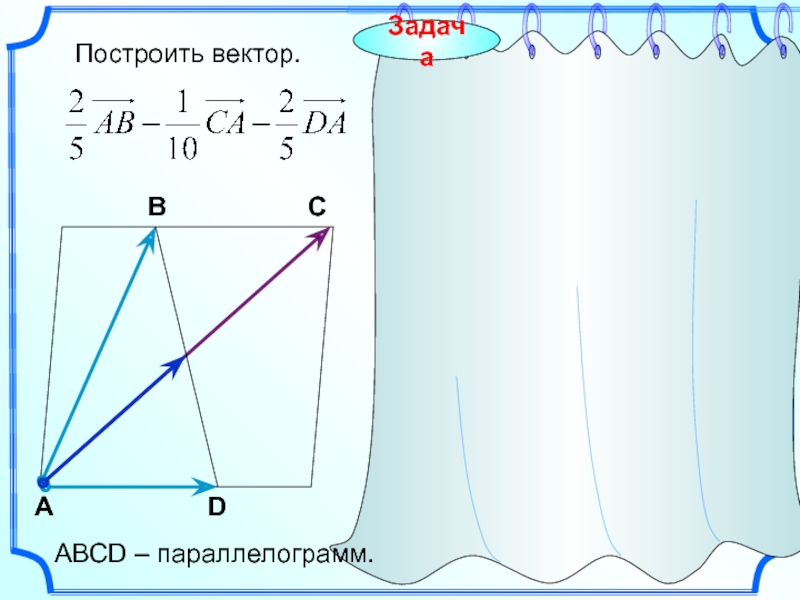
- 12. В С ABCD – параллелограмм.
- 13. Умножение вектора на число обладает следующими основными
- 14. Рисунок иллюстрирует
- 15. B Рисунок иллюстрирует первый распределительный закон. Представлен
- 16. O Второй распределительный закон 3
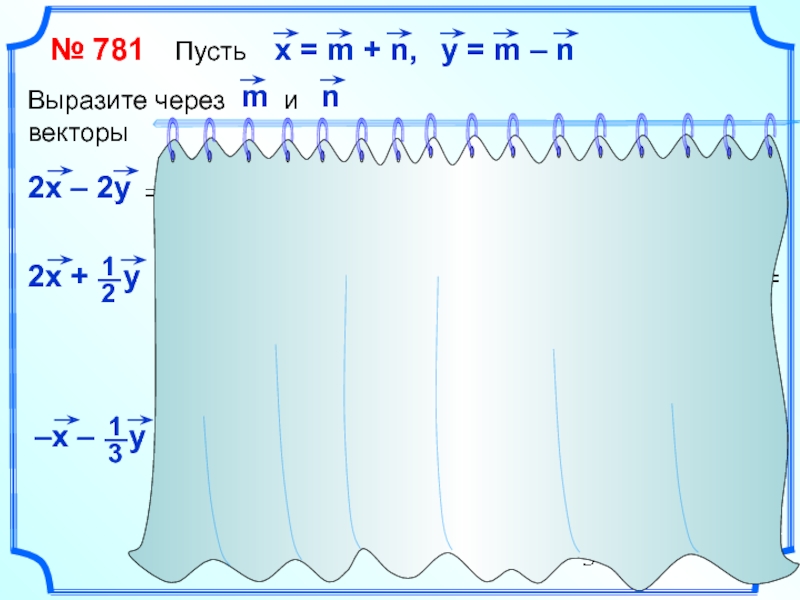
- 17. № 781 Пусть
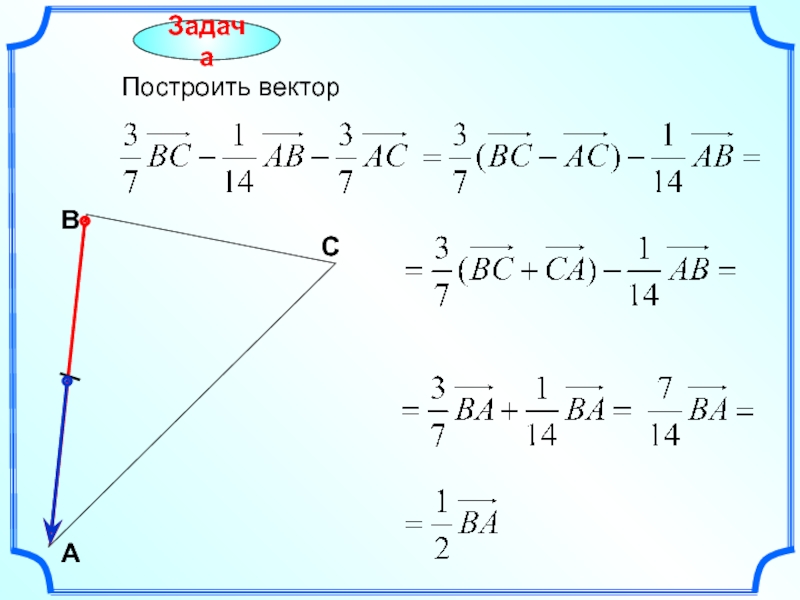
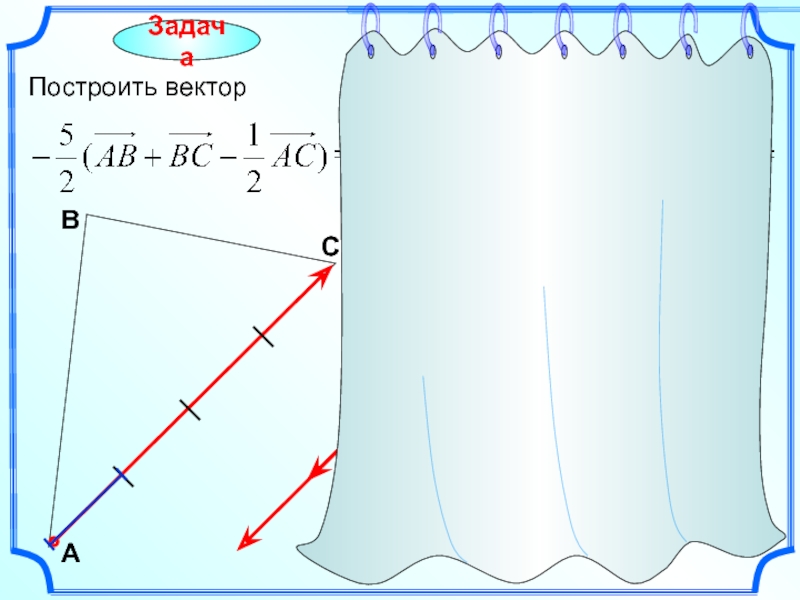
- 18. Задача Построить вектор С А В
- 19. Задача Построить вектор С А В
- 20. Задача Построить вектор. С А В
- 21. Построить вектор. С А В
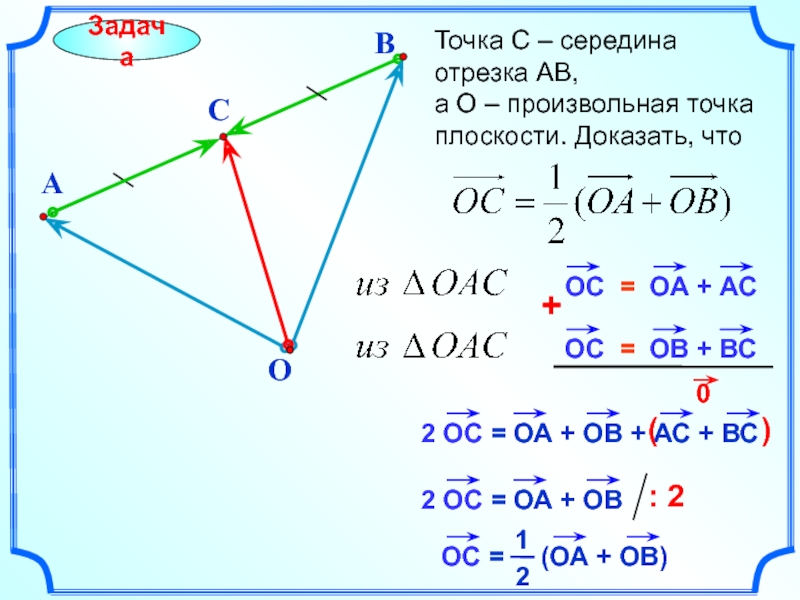
- 22. B Точка С – середина отрезка
- 23. A
- 24. Теорема Средняя линия трапеции параллельна основаниям
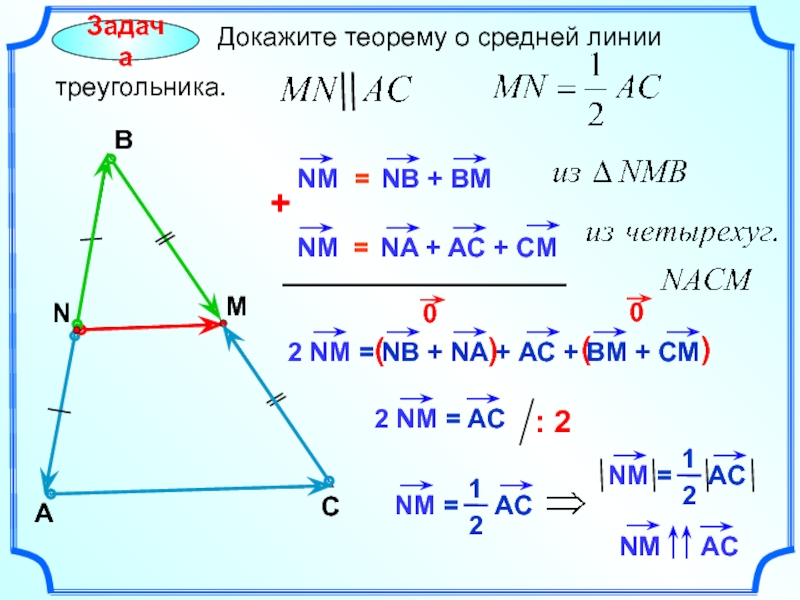
- 25. Правило многоугольника A
- 26. Задача
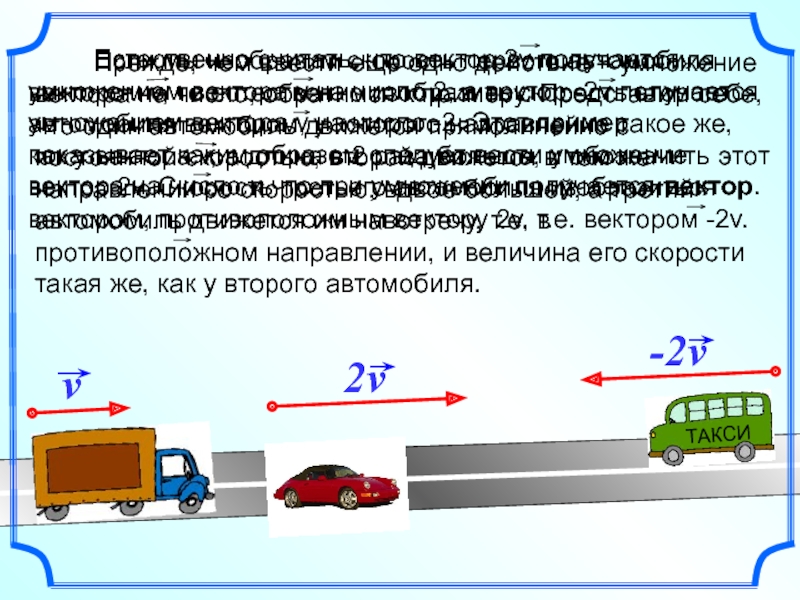
Слайд 2 Прежде, чем ввести еще одно действие –
Слайд 5Умножение вектора на число.
Произведение любого вектора на число нуль есть нулевой
Произведение нулевого вектора на любое число считается нулевой вектор.
Слайд 13Умножение вектора на число обладает следующими основными свойствами.
Сочетательный закон
Первый распределительный закон
Второй
1
2
3
Слайд 14
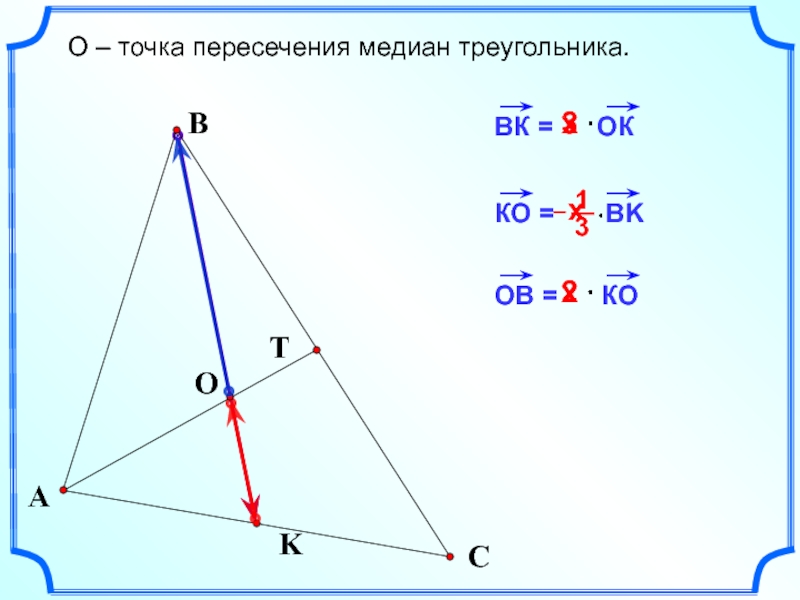
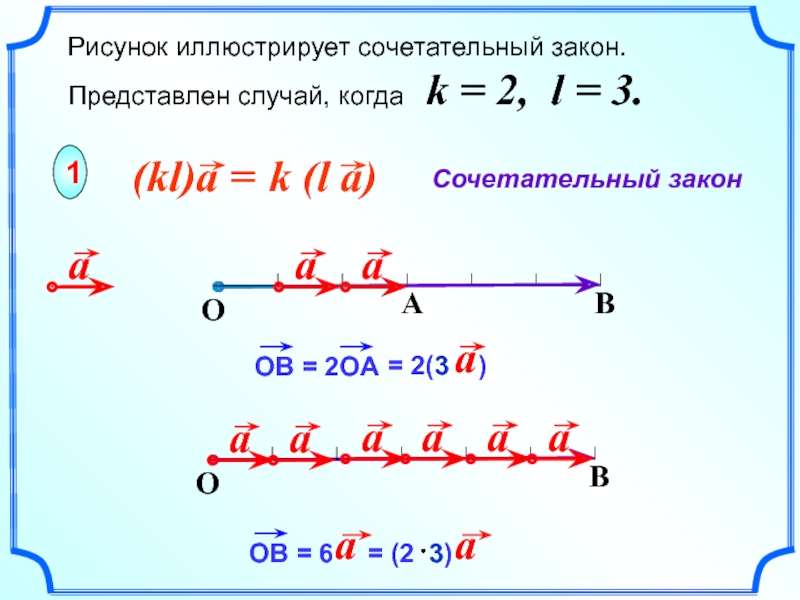
Рисунок иллюстрирует сочетательный закон. Представлен случай, когда k = 2,
Сочетательный закон
1
B
O
Слайд 15B
Рисунок иллюстрирует первый распределительный закон. Представлен случай, когда k =
O
Первый распределительный закон
2
OB =
Слайд 16
O
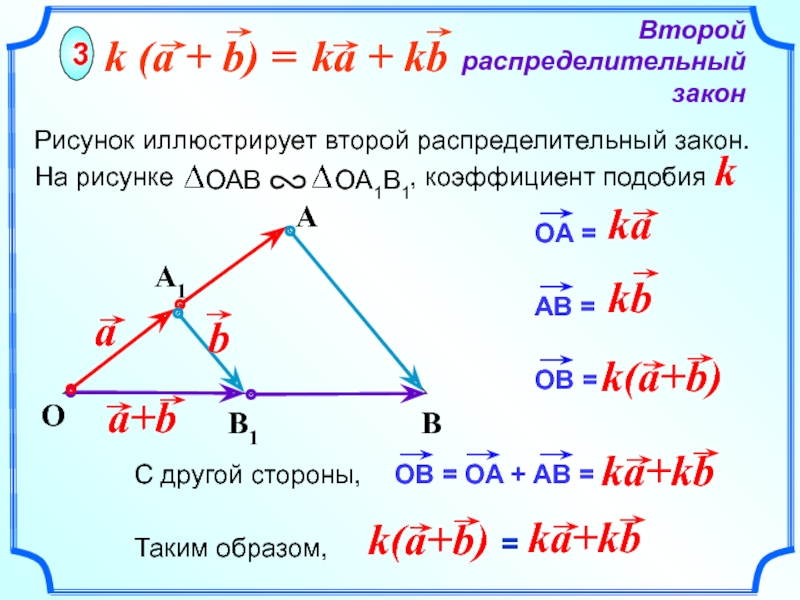
Второй распределительный закон
3
A
Рисунок иллюстрирует второй распределительный закон.
На рисунке
k
A1
B1
B
С другой стороны,
Таким образом,
=
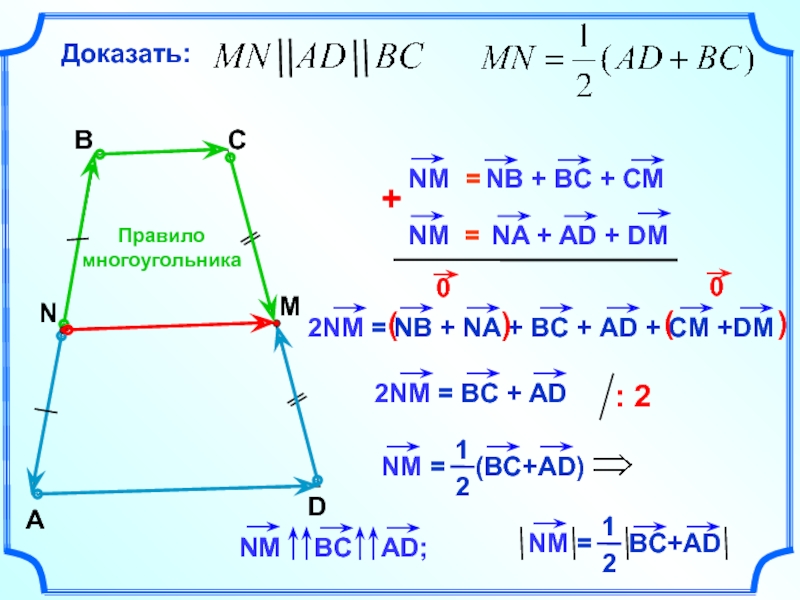
Слайд 24Теорема
Средняя линия трапеции параллельна
основаниям и равна их полусумме.
Дано:
трапеция АВСD,
Доказать:
Слайд 26
Задача
К – середина DC, АВ = , AD = . Выразите через
векторы и векторы:
С
А
В
D