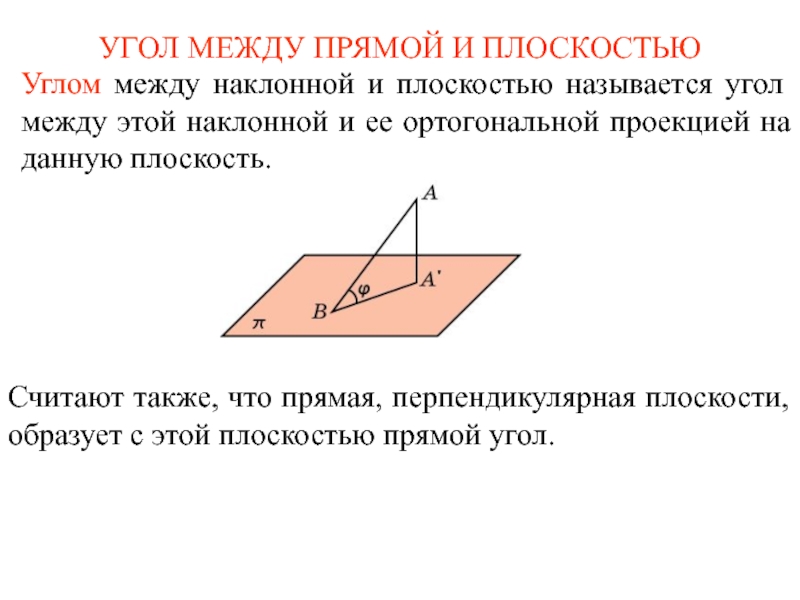
Считают также, что прямая, перпендикулярная плоскости, образует с этой плоскостью прямой угол.
- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Угол между прямой и плоскостью. Упражнения презентация
Содержание
- 1. Угол между прямой и плоскостью. Упражнения
- 2. Теорема Угол между наклонной и плоскостью является
- 3. Упражнение 1 Прямые a и b образуют
- 4. Упражнение 2 Две плоскости образуют с данной
- 5. Упражнение 3 Под каким углом к плоскости
- 6. Упражнение 4 Может ли катет равнобедренного прямоугольного
- 7. Упражнение 5 Одна из двух скрещивающихся прямых
- 8. Упражнение 6 Будут ли в пирамиде боковые
- 9. Упражнение 7 Через сторону квадрата проведена плоскость,
- 10. Упражнение 8 Основание равнобедренного треугольника лежит в
- 11. Упражнение 9 Из вершины A квадрата ABCD
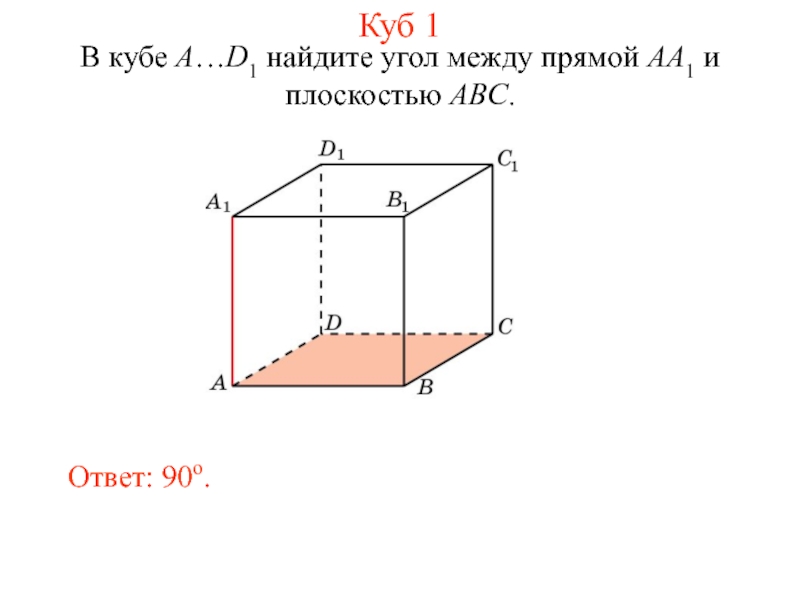
- 12. В кубе A…D1 найдите угол между прямой AA1 и плоскостью ABC. Ответ: 90o. Куб 1
- 13. В кубе A…D1 найдите угол между прямой AA1 и плоскостью AB1C1. Ответ: 45o. Куб 2
- 14. В кубе A…D1 найдите тангенс угла между прямой AA1 и плоскостью BC1D. Куб 3
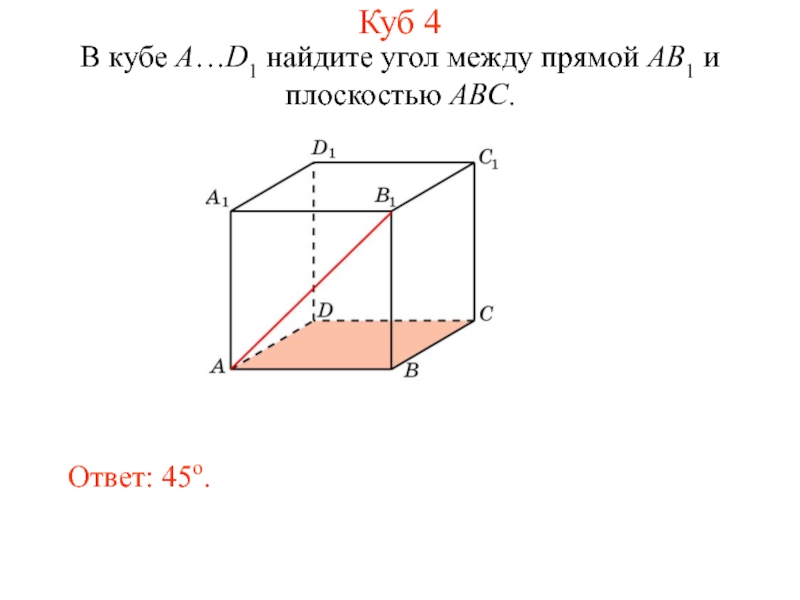
- 15. В кубе A…D1 найдите угол между прямой AB1 и плоскостью ABC. Ответ: 45o. Куб 4
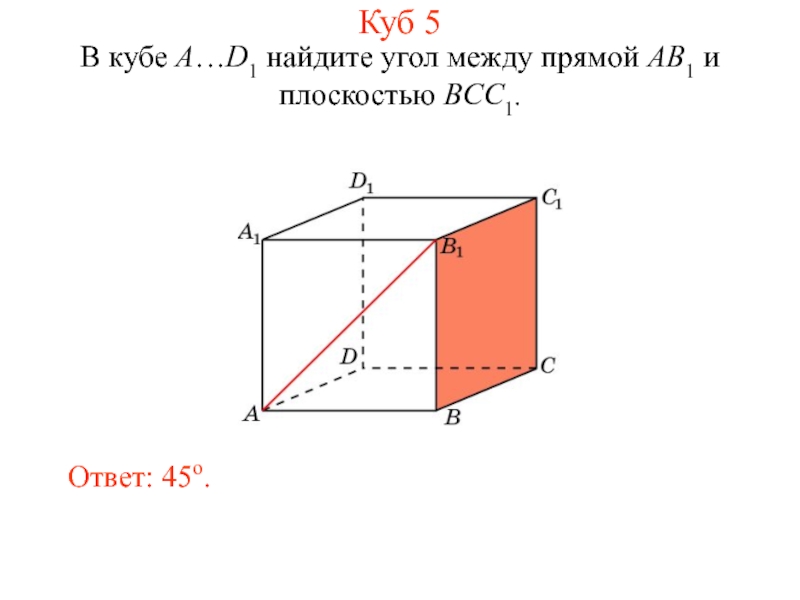
- 16. В кубе A…D1 найдите угол между прямой AB1 и плоскостью BCC1. Ответ: 45o. Куб 5
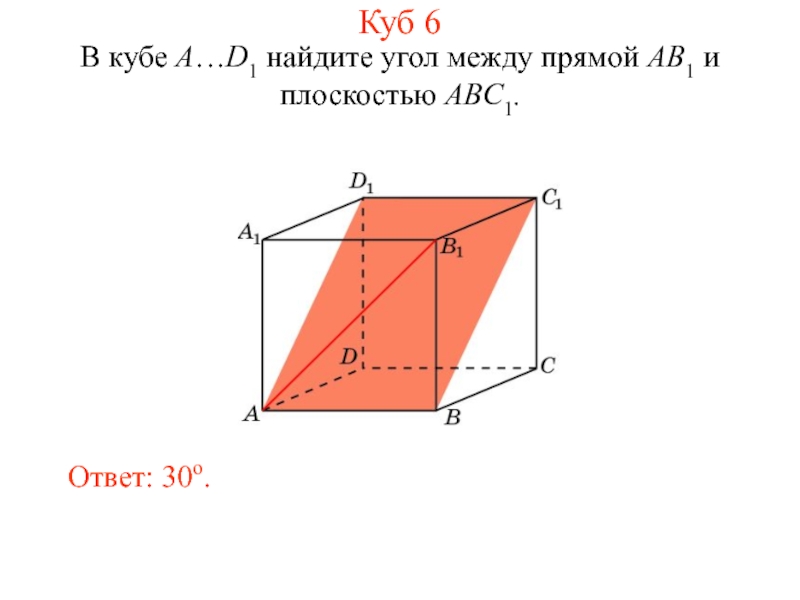
- 17. В кубе A…D1 найдите угол между прямой
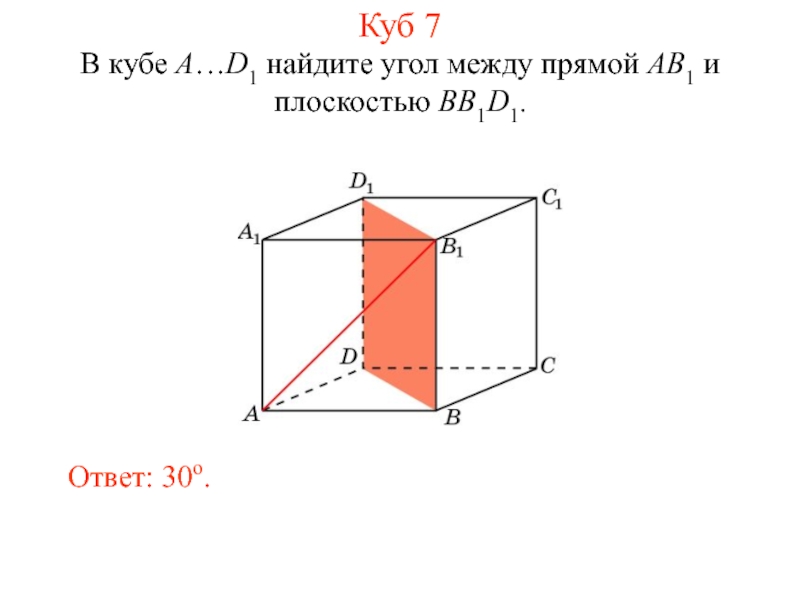
- 18. В кубе A…D1 найдите угол между прямой AB1 и плоскостью BB1D1. Ответ: 30o. Куб 7
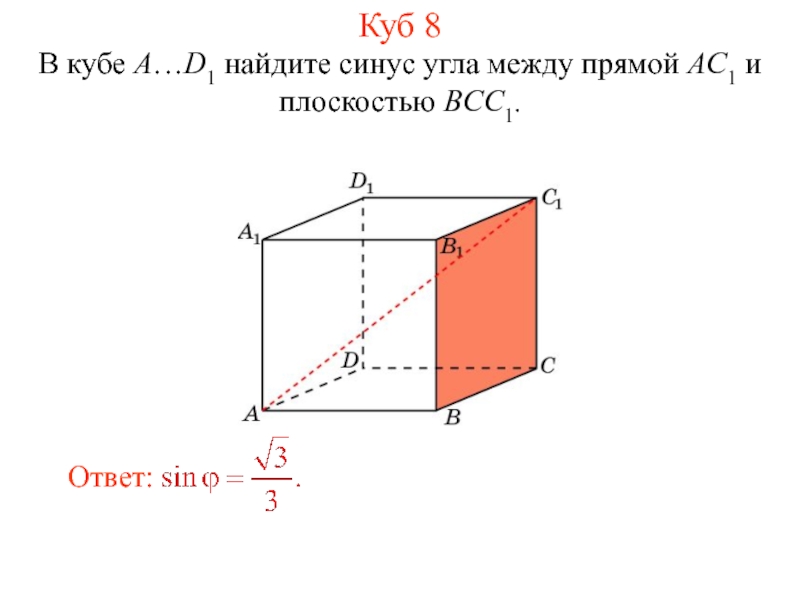
- 19. В кубе A…D1 найдите синус угла между прямой AC1 и плоскостью BCC1. Куб 8
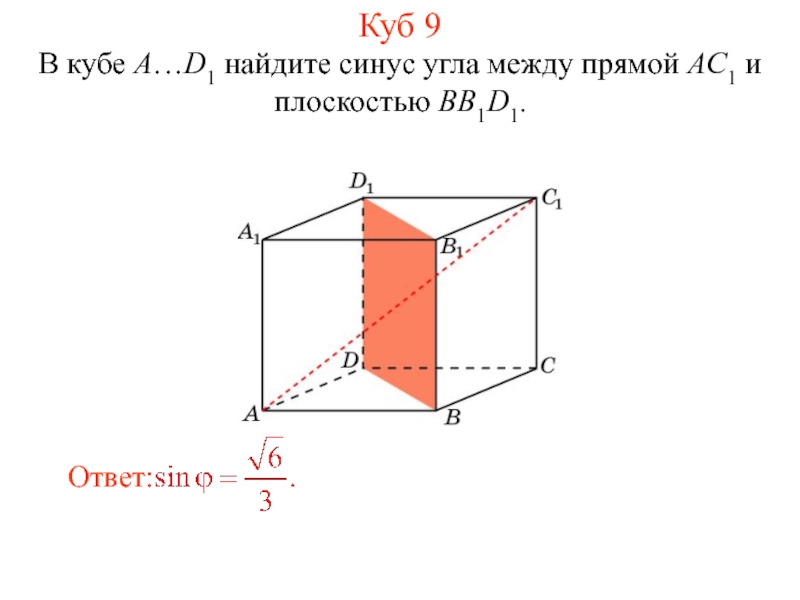
- 20. В кубе A…D1 найдите синус угла между прямой AC1 и плоскостью BB1D1. Куб 9
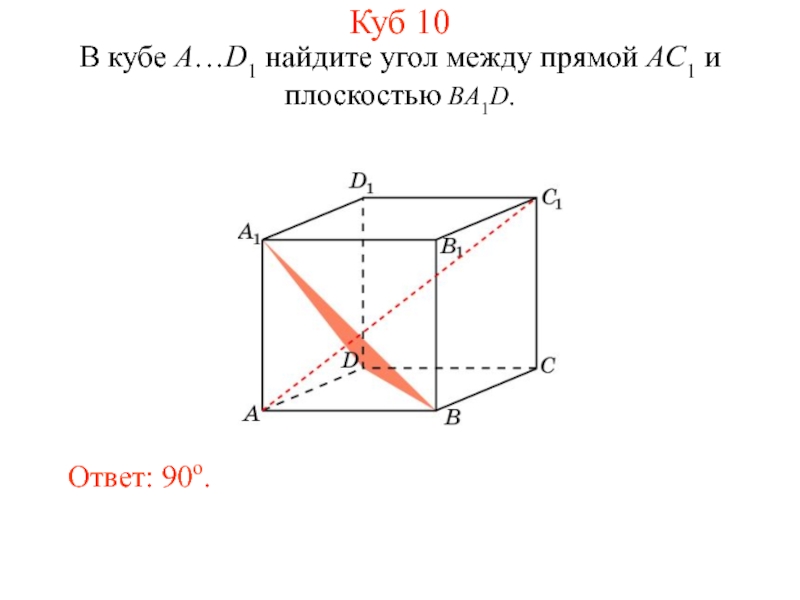
- 21. В кубе A…D1 найдите угол между прямой AC1 и плоскостью BA1D. Ответ: 90o. Куб 10
- 22. В правильном тетраэдре ABCD точка E –
- 23. В правильном тетраэдре ABCD найдите косинус угла между прямой AD и плоскостью ABC. Пирамида 2
- 24. В правильной пирамиде SABCD, все ребра которой
- 25. В правильной пирамиде SABCD, все ребра которой
- 26. В правильной пирамиде SABCD, все ребра которой
- 27. В правильной 6-ой пирамиде SA…F, боковые ребра
- 28. В правильной 6-ой пирамиде SA…F, боковые ребра
- 29. В правильной 6-ой пирамиде SA…F, боковые ребра
- 30. В правильной 6-ой пирамиде SA…F, боковые ребра
- 31. В правильной 6-ой пирамиде SA…F, боковые ребра
- 32. В правильной треугольной призме ABCA1B1C1, все ребра
- 33. В правильной треугольной призме ABCA1B1C1, все ребра
- 34. В правильной треугольной призме ABCA1B1C1, все ребра
- 35. В правильной треугольной призме ABCA1B1C1, все ребра
- 36. В правильной треугольной призме ABCA1B1C1, все ребра
- 37. В правильной треугольной призме ABCA1B1C1, все ребра
- 38. В правильной 6-й призме A…F1, ребра которой
- 39. В правильной 6-й призме A…F1, ребра которой
- 40. В правильной 6-й призме A…F1, ребра которой
- 41. В правильной 6-й призме A…F1, ребра которой
- 42. В правильной 6-й призме A…F1, ребра которой
- 43. В правильной 6-й призме A…F1, ребра которой
- 44. В правильной 6-й призме A…F1, ребра которой
- 45. В правильной 6-й призме A…F1, ребра которой
- 46. В правильной 6-й призме A…F1, ребра которой
- 47. В правильной 6-й призме A…F1, ребра которой
- 48. В правильной 6-й призме A…F1, ребра которой
- 49. В правильной 6-й призме A…F1, ребра которой
- 50. В правильной 6-й призме A…F1, ребра которой
- 51. В правильной 6-й призме A…F1, ребра которой
- 52. В правильной 6-й призме A…F1, ребра которой
Слайд 1УГОЛ МЕЖДУ ПРЯМОЙ И ПЛОСКОСТЬЮ
Углом между наклонной и плоскостью называется угол
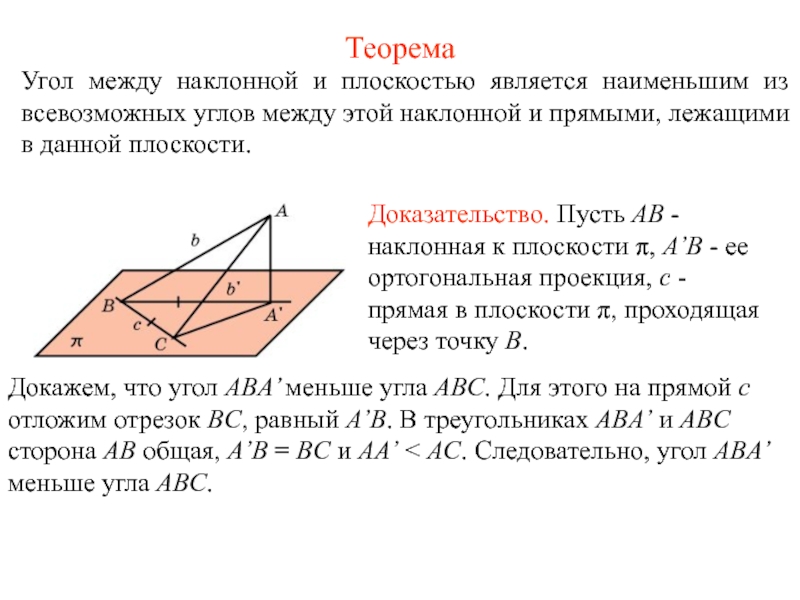
Слайд 2Теорема
Угол между наклонной и плоскостью является наименьшим из всевозможных углов между
Слайд 3Упражнение 1
Прямые a и b образуют с плоскостью α равные углы.
Ответ: Нет.
Слайд 4Упражнение 2
Две плоскости образуют с данной прямой равные углы. Как расположены
Ответ: Параллельны или пересекаются.
Слайд 5Упражнение 3
Под каким углом к плоскости нужно провести отрезок, чтобы его
Ответ: 60о.
Слайд 6Упражнение 4
Может ли катет равнобедренного прямоугольного треугольника образовать с плоскостью, проходящей
Ответ: Нет, 45о.
Слайд 7Упражнение 5
Одна из двух скрещивающихся прямых пересекает плоскость под углом 60°,
Ответ: 30о.
Слайд 8Упражнение 6
Будут ли в пирамиде боковые ребра равны, если они образуют
Ответ: Да.
Слайд 9Упражнение 7
Через сторону квадрата проведена плоскость, составляющая с диагональю квадрата угол
Ответ: 45о.
Слайд 10Упражнение 8
Основание равнобедренного треугольника лежит в плоскости π (плоскость треугольника не
Ответ: Угол наклона высоты.
Слайд 11Упражнение 9
Из вершины A квадрата ABCD перпендикулярно его плоскости проведен отрезок
Ответ: 30о.
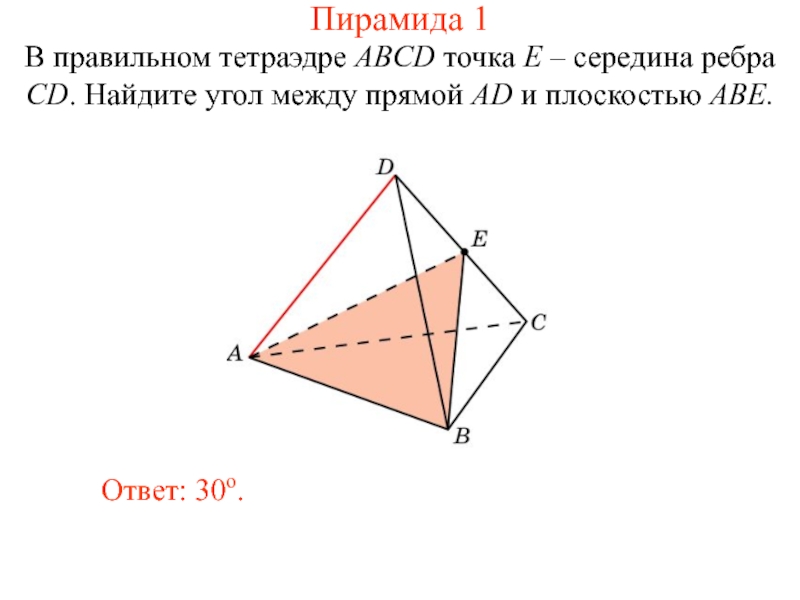
Слайд 22В правильном тетраэдре ABCD точка E – середина ребра CD. Найдите
Ответ: 30о.
Пирамида 1
Слайд 23В правильном тетраэдре ABCD найдите косинус угла между прямой AD и
Пирамида 2
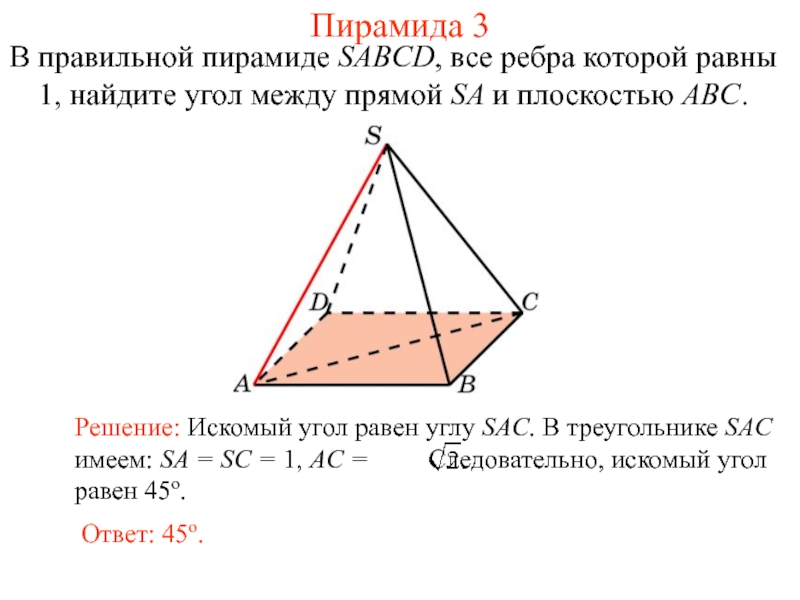
Слайд 24В правильной пирамиде SABCD, все ребра которой равны 1, найдите угол
Пирамида 3
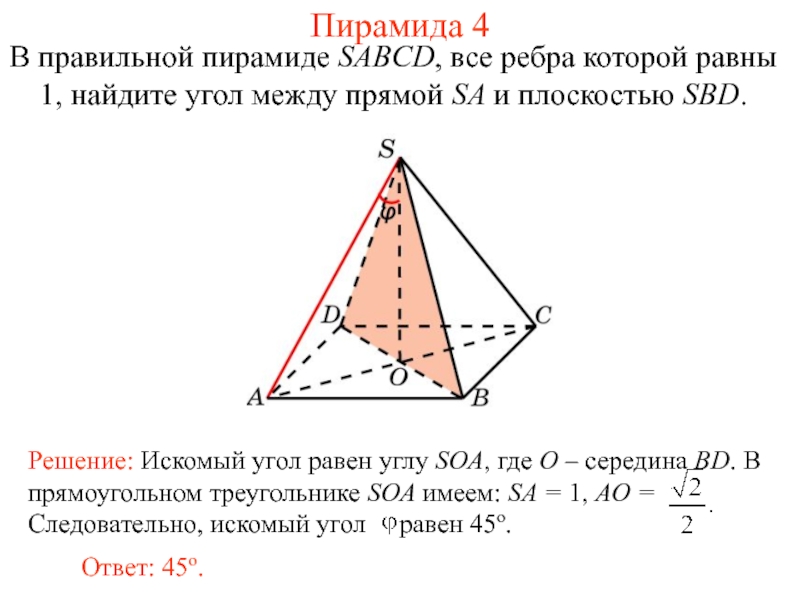
Слайд 25В правильной пирамиде SABCD, все ребра которой равны 1, найдите угол
Пирамида 4
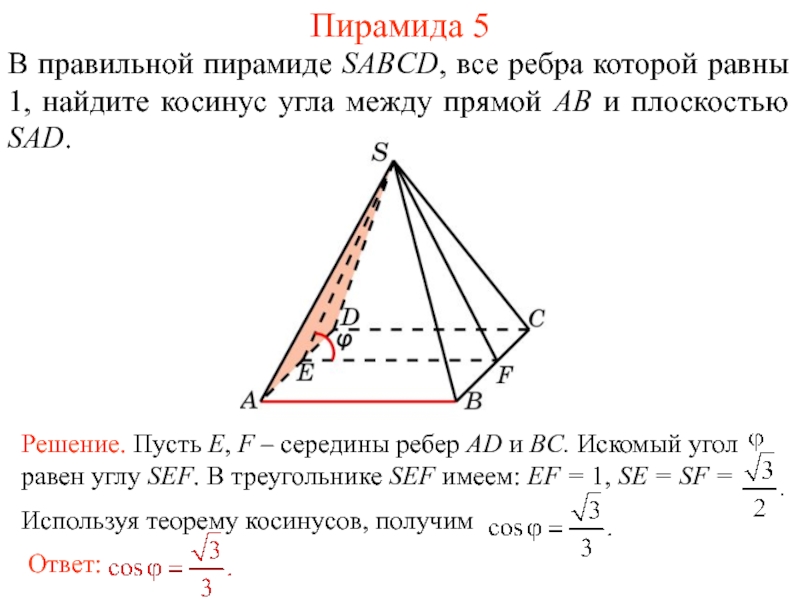
Слайд 26В правильной пирамиде SABCD, все ребра которой равны 1, найдите косинус
Пирамида 5
Слайд 27В правильной 6-ой пирамиде SA…F, боковые ребра которой равны 2, а
Пирамида 6
Слайд 28В правильной 6-ой пирамиде SA…F, боковые ребра которой равны 2, а
Пирамида 7
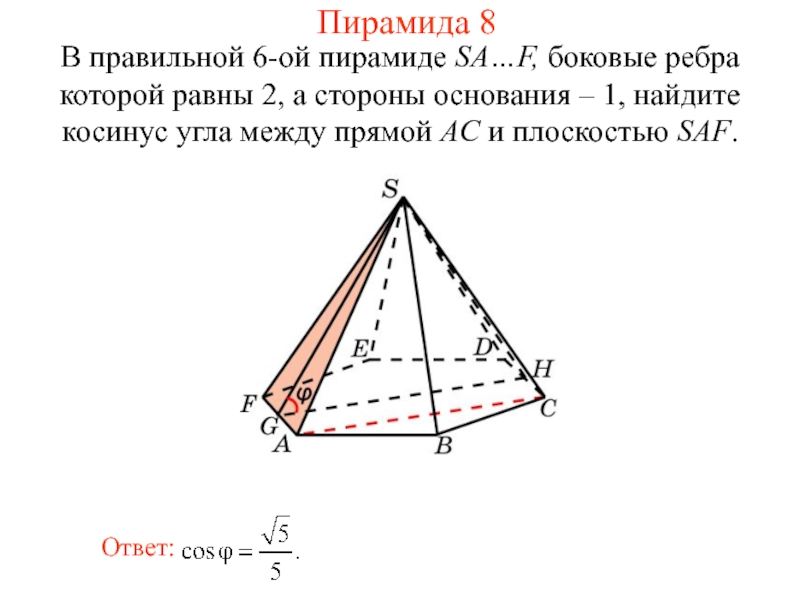
Слайд 29В правильной 6-ой пирамиде SA…F, боковые ребра которой равны 2, а
Пирамида 8
Слайд 30В правильной 6-ой пирамиде SA…F, боковые ребра которой равны 2, а
Пирамида 9*
Слайд 31В правильной 6-ой пирамиде SA…F, боковые ребра которой равны 2, а
Пирамида 10*
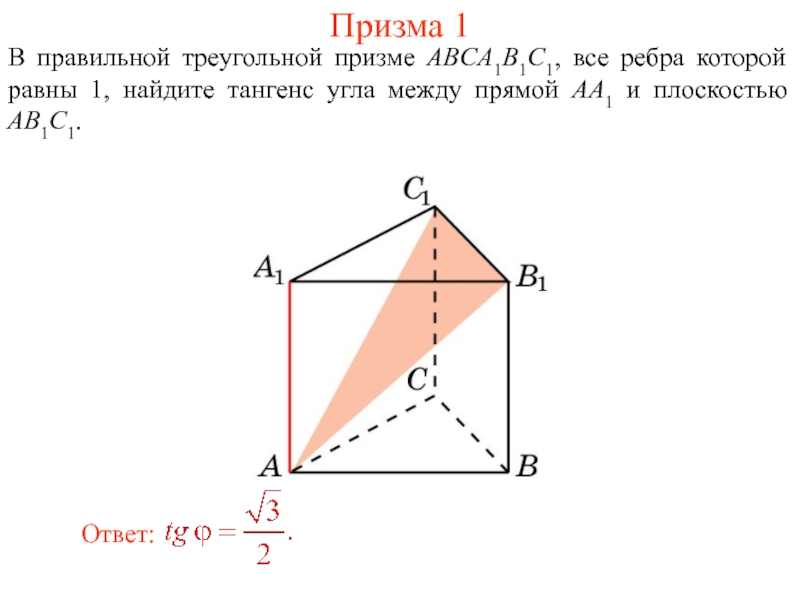
Слайд 32В правильной треугольной призме ABCA1B1C1, все ребра которой равны 1, найдите
Призма 1
Слайд 33В правильной треугольной призме ABCA1B1C1, все ребра которой равны 1, найдите
Призма 2
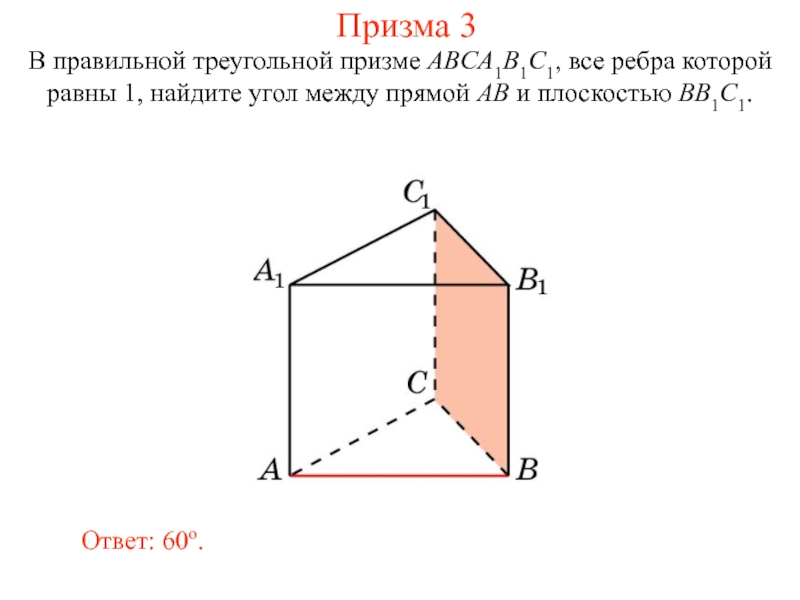
Слайд 34В правильной треугольной призме ABCA1B1C1, все ребра которой равны 1, найдите
Ответ: 60o.
Призма 3
Слайд 35В правильной треугольной призме ABCA1B1C1, все ребра которой равны 1, найдите
Призма 4
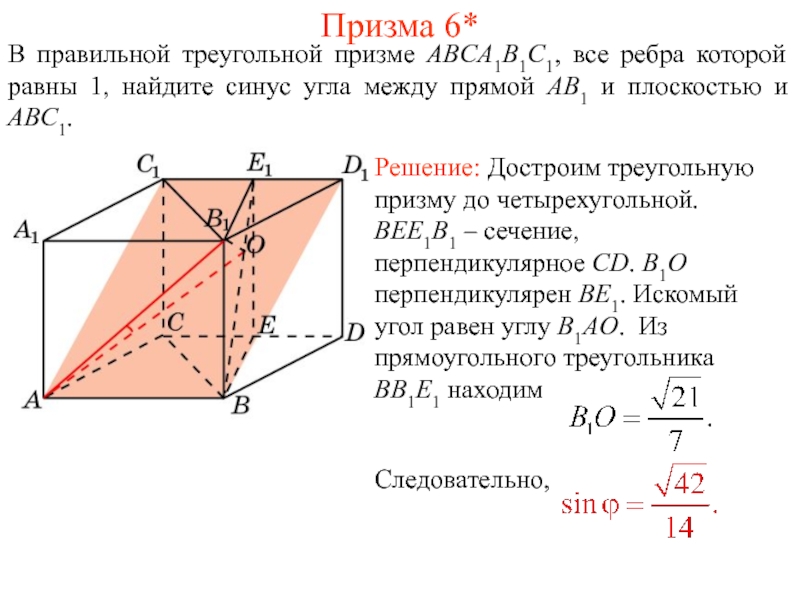
Слайд 36В правильной треугольной призме ABCA1B1C1, все ребра которой равны 1, найдите
Призма 5*
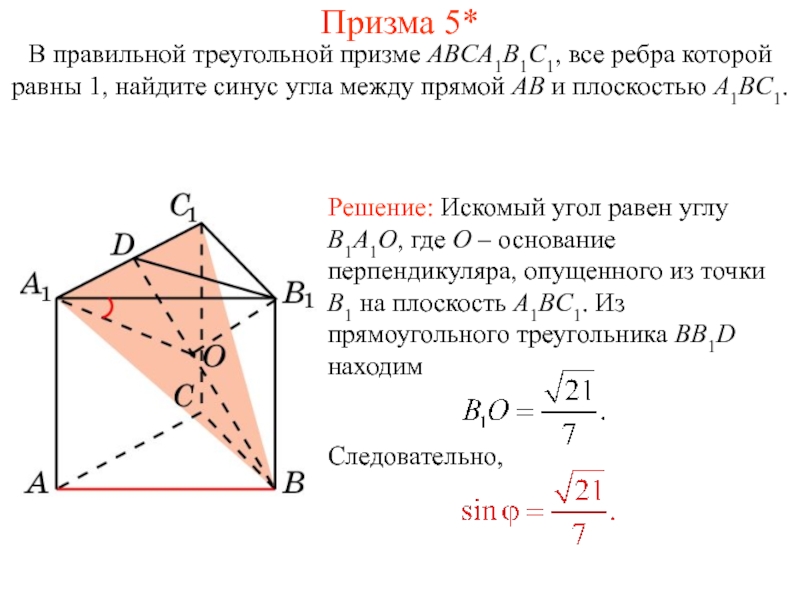
Слайд 37В правильной треугольной призме ABCA1B1C1, все ребра которой равны 1, найдите
Призма 6*
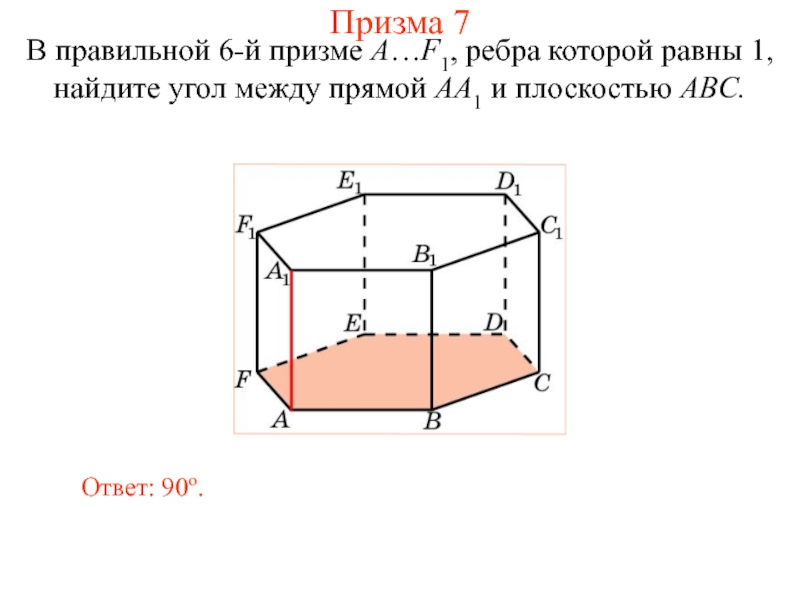
Слайд 38В правильной 6-й призме A…F1, ребра которой равны 1, найдите угол
Ответ: 90о.
Призма 7
Слайд 39В правильной 6-й призме A…F1, ребра которой равны 1, найдите угол
Ответ: 45о.
Призма 8
Слайд 40В правильной 6-й призме A…F1, ребра которой равны 1, найдите угол
Призма 9
Слайд 41В правильной 6-й призме A…F1, ребра которой равны 1, найдите тангенс
Призма 10
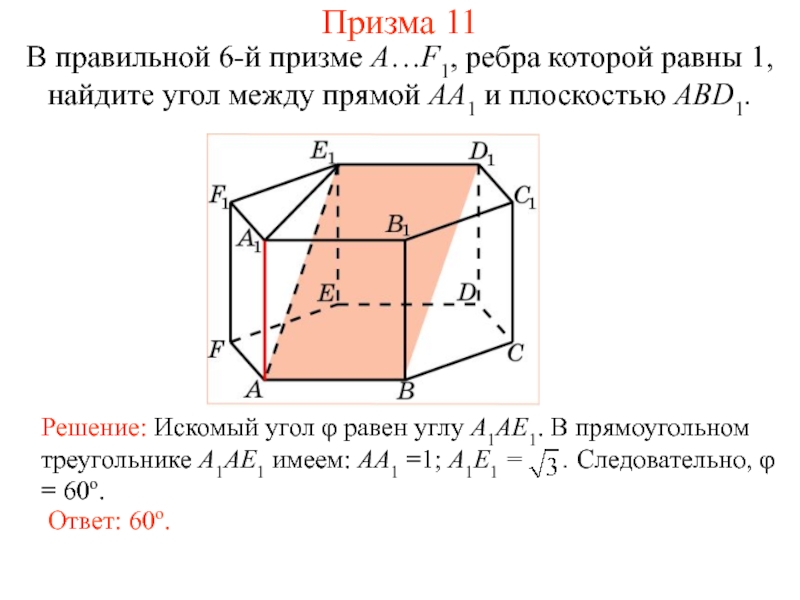
Слайд 42В правильной 6-й призме A…F1, ребра которой равны 1, найдите угол
Призма 11
Слайд 43В правильной 6-й призме A…F1, ребра которой равны 1, найдите тангенс
Призма 12
Слайд 44В правильной 6-й призме A…F1, ребра которой равны 1, найдите угол
Призма 13
Слайд 45В правильной 6-й призме A…F1, ребра которой равны 1, найдите тангенс
Призма 14
Слайд 46В правильной 6-й призме A…F1, ребра которой равны 1, найдите тангенс
Призма 15
Слайд 47В правильной 6-й призме A…F1, ребра которой равны 1, найдите синус
Призма 16*
Слайд 48В правильной 6-й призме A…F1, ребра которой равны 1, найдите синус
Призма 17*
Слайд 49В правильной 6-й призме A…F1, ребра которой равны 1, найдите синус
Призма 18*
Слайд 50В правильной 6-й призме A…F1, ребра которой равны 1, найдите синус
Призма 19*
Слайд 51В правильной 6-й призме A…F1, ребра которой равны 1, найдите синус
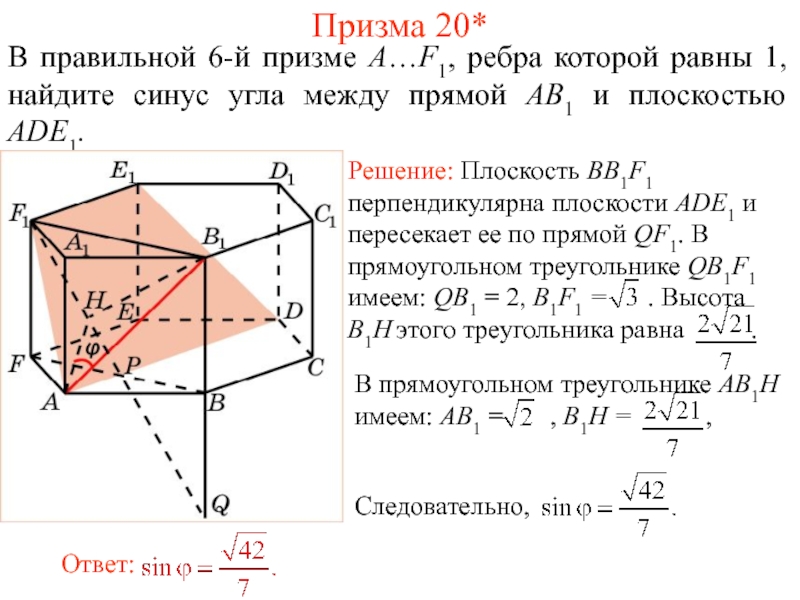
Призма 20*
Слайд 52В правильной 6-й призме A…F1, ребра которой равны 1, найдите синус
Призма 21*