остается грамматикой архитектора»
Ле Корбюзье
- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Цилиндр и конус, описанные около многогранника презентация
Содержание
- 1. Цилиндр и конус, описанные около многогранника
- 2. Ивановская медицинская академия Свято – Введенский собор Фабрика Ивановский государственный университет Квадросити
- 3. ЦИЛИНДР И КОНУС, ОПИСАННЫЕ ОКОЛО МНОГОГРАННИКА ПРИЗМА
- 4. ПИРАМИДА называется ВПИСАННОЙ В КОНУС (а КОНУС
- 5. Для любого треугольника: R=… Для любого треугольника:
- 6. №1. Вокруг правильной четырехугольной призмы описан цилиндр.
- 7. №2. Сторона основания правильной треугольной
- 8. ДОМАШНЕЕ ЗАДАНИЕ теория: записи в тетради Практика:
- 9. Литература и интернет- ресурсы 1. Геометрия:
Ивановская медицинская академия Свято – Введенский собор Фабрика Ивановский государственный университет Квадросити
Слайд 1АРХИТЕКТУРА-ЭТО ОСМЫСЛЕННАЯ ГЕОМЕТРИЯ
«Прошли века, но роль геометрии не изменилась.
Она по-прежнему
Слайд 2Ивановская медицинская академия
Свято – Введенский собор
Фабрика
Ивановский государственный университет
Квадросити
Слайд 3ЦИЛИНДР И КОНУС, ОПИСАННЫЕ ОКОЛО МНОГОГРАННИКА
ПРИЗМА называется ВПИСАННОЙ В ЦИЛИНДР (а
ЦИЛИНДР ОПИСАННЫМ ОКОЛО ПРИЗМЫ), если ее основания-многоугольники, вписанные в окружности оснований цилиндра, а боковые ребра совпадают с образующими цилиндра
В цилиндр можно вписать только такую призму, основания которой можно вписать в окружность.
Замечания:
Высота призмы равна высоте описанного около нее цилиндра
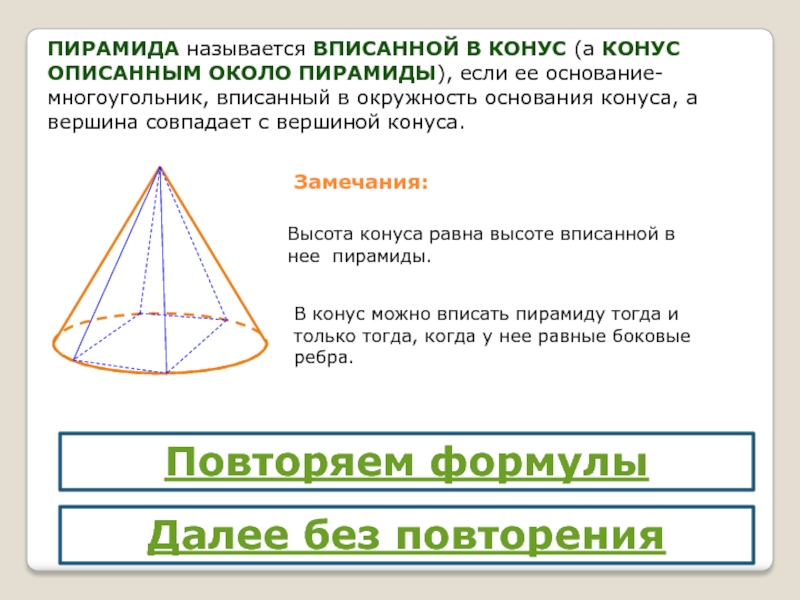
Слайд 4ПИРАМИДА называется ВПИСАННОЙ В КОНУС (а КОНУС ОПИСАННЫМ ОКОЛО ПИРАМИДЫ), если
ее основание-многоугольник, вписанный в окружность основания конуса, а вершина совпадает с вершиной конуса.
Замечания:
Высота конуса равна высоте вписанной в нее пирамиды.
В конус можно вписать пирамиду тогда и только тогда, когда у нее равные боковые ребра.
Повторяем формулы
Далее без повторения
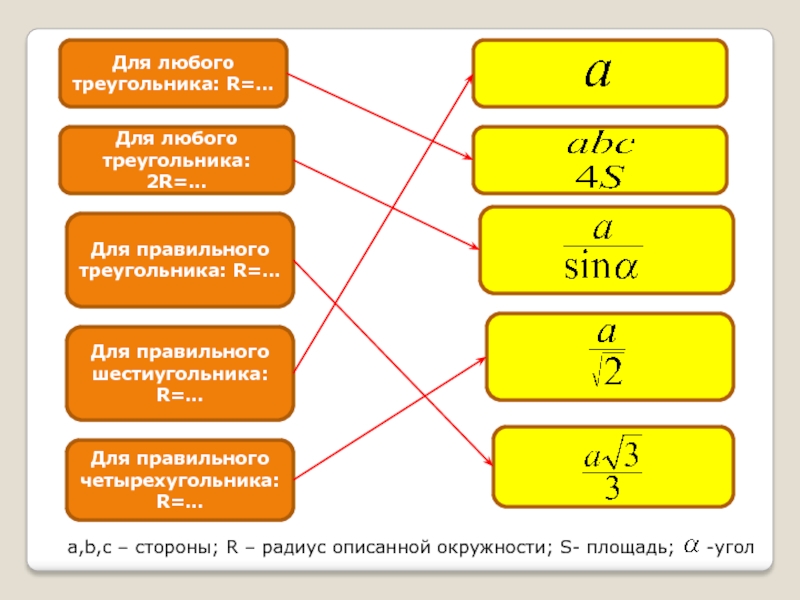
Слайд 5Для любого треугольника: R=…
Для любого треугольника: 2R=…
Для правильного треугольника: R=…
Для правильного
шестиугольника: R=…
Для правильного четырехугольника: R=…
a,b,c – стороны; R – радиус описанной окружности; S- площадь; -угол
Слайд 6№1. Вокруг правильной четырехугольной призмы описан цилиндр. Найти площадь его боковой
поверхности, если высота призмы равна 24 см, а диагональ боковой грани 26 см.
А
B
C
D
A1
B1
C1
D1
O
O1
Дано: ABCDA1B1C1D1 – правильная призма
ВВ1=24 см, В1С=26 см
описанный цилиндр
Найти: Sбоковой поверхности цилиндра
Анализ условий:
Sбоковой поверхности цилиндра=
R=AO (AO-половина диагонали АС квадрата ABCD)
BC-? (из ∆ВВ1С)
; H=BB1
Из ∆ВВ1С- прямоугольного по теореме Пифагора: ВС=10 см.
Из ∆АВС- прямоугольного и равнобедренного: АС= см.Значит, АО= (см)
Sбоковой поверхности цилиндра= = =
(см2).
Решение:
Ответ:
(см2).
Слайд 7
№2. Сторона основания правильной треугольной пирамиды равна 8√3 см, а боковые
грани наклонены к основанию под углом 450. Найти площадь боковой поверхности описанного около пирамиды конуса.
Дано: конус с вершиной Р, вписана правильная пирамида РАВС,
АВ= 8√3 см, (РАВ)^(АВС)= 450
Найти: Sбоковой поверхности конуса
Р
О
А
В
С
К
Анализ условий:
1. Sбоковой пов.конуса= Rl, R=?, l=?, R=CO
2. l=PB, дополнительно требуется узнать PO=?
3. Из ∆РКО: РО, зная КО=R:2
4. Из ∆РОВ: РВ
1. Т.к. ∆АВС – равносторонний, то СО=R, значит, СО=8 см.
r=ОК=R:2=4 (см)
2. Из ∆РОК – прямоугольного и равнобедренного: РО=4 см.
3. Из ∆РОВ- прямоугольного по теореме Пифагора: РВ=√80 см
4. Следовательно: Sбоковой пов.конуса= Rl= ∙8∙√80=32√5 (см2)
Решение:
Ответ:
32√5 (см2)
Слайд 8ДОМАШНЕЕ ЗАДАНИЕ
теория: записи в тетради
Практика:
2.1. №630
2.2. Детская игрушка – калейдоскоп- представляет
собой цилиндрическую трубку с размещенными внутрь цветными зеркалами. Пусть зеркала расположены в форме правильного треугольника со стороной 2 см. Длина трубки 5 см. Сколько краски потребуется на отделку боковой поверхности трубки, если на 1 см2 расходуется 0,8 г. краски? Результат округлите до десятых.
Слайд 9Литература и
интернет- ресурсы
1. Геометрия: Учебник для 10-11 классов средней школы/
Л.С. Атанасян и др.-М.:Просвещение, 1994
2. Зив Б.Г. И др. Задачи по геометрии для 7-11 классов /Б.Г. Зив, В.М. Мейлер, А.Г. Баханский.-М.:Просвещение, 1991
3. Фотографии, размещенные на слайде 1:
http://img-fotki.yandex.ru/get/3200/painkiller-302.2/0_1d1c4_1049c0f0_XL
http://s60.radikal.ru/i170/0909/e9/8fffcaf44f4b.jpg
http://www.tourgenius.ru/drp/f/file/391454993/ivanovo.jpg
http://www.stroyinvest-iv.ru/gal/Objects/1.jpg
http://www.kn37.ru/Rent/kvadro.jpg
2. Зив Б.Г. И др. Задачи по геометрии для 7-11 классов /Б.Г. Зив, В.М. Мейлер, А.Г. Баханский.-М.:Просвещение, 1991
3. Фотографии, размещенные на слайде 1:
http://img-fotki.yandex.ru/get/3200/painkiller-302.2/0_1d1c4_1049c0f0_XL
http://s60.radikal.ru/i170/0909/e9/8fffcaf44f4b.jpg
http://www.tourgenius.ru/drp/f/file/391454993/ivanovo.jpg
http://www.stroyinvest-iv.ru/gal/Objects/1.jpg
http://www.kn37.ru/Rent/kvadro.jpg
