среды, системы электронного обучения Гиперметод
learn.urfu.ru
- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Линейная алгебра презентация
Содержание
- 1. Линейная алгебра
- 2. ПЛАН ЛЕКЦИИ Определение и виды
- 3. 1. МАТРИЦЫ И ДЕЙСТВИЯ НАД НИМИ
- 4. ОПРЕДЕЛЕНИЯ Прямоугольной матрицей
- 5. ВИДЫ МАТРИЦ
- 6. ПРИНЦИП НУМЕРАЦИИ СТРОК И СТОЛБЦОВ
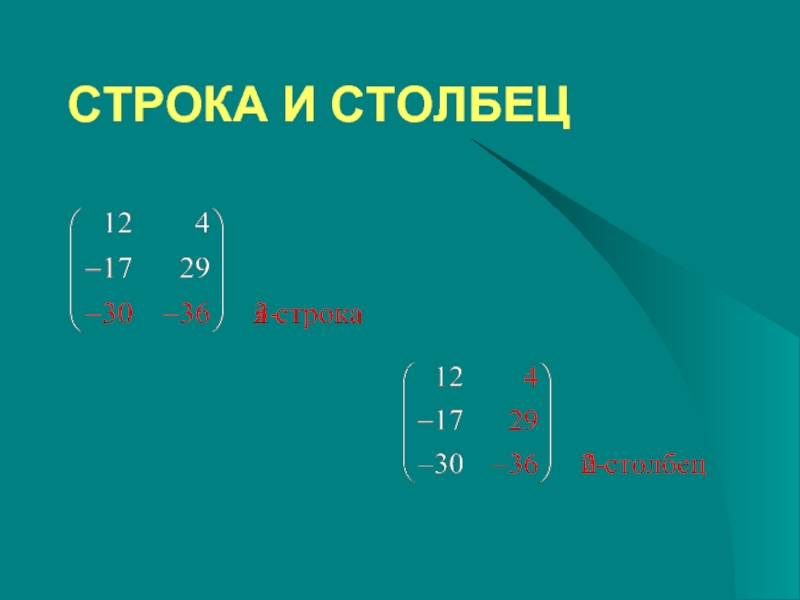
- 7. СТРОКА И СТОЛБЕЦ
- 8. РАЗМЕР МАТРИЦЫ МАТРИЦА, ИМЕЮЩАЯ m СТРОК И
- 9. ОБЩИЙ ВИД МАТРИЦЫ РАЗМЕРА m НА n
- 10. ЭЛЕМЕНТ МАТРИЦЫ
- 11. ДИАГОНАЛИ КВАДРАТНЫХ МАТРИЦ
- 12. ТРЕУГОЛЬНЫЕ МАТРИЦЫ
- 13. ОПЕРАЦИИ НАД МАТРИЦАМИ
- 14. ЛЮБУЮ МАТРИЦУ МОЖНО УМНОЖИТЬ НА ЧИСЛО
- 15. МАТРИЦЫ ОДИНАКОВОГО РАЗМЕРА МОЖНО СКЛАДЫВАТЬ И ВЫЧИТАТЬ
- 16. ТРАНСПОНИРОВАНИЕ МАТРИЦЫ
- 17. УМНОЖЕНИЕ СТРОКИ НА СТОЛБЕЦ (СКАЛЯРНОЕ ПРОИЗВЕДЕНИЕ)
- 18. УМНОЖЕНИЕ МАТРИЦЫ НА СТОЛБЕЦ
- 19. ВОЗМОЖНОСТЬ УМНОЖЕНИЯ МАТРИЦЫ НА МАТРИЦУ
- 20. ПРАВИЛО УМНОЖЕНИЯ МАТРИЦЫ
- 21. ПРИМЕР УМНОЖЕНИЯ МАТРИЦ
- 22. УМНОЖЕНИЕ СТОЛБЦА НА СТРОКУ
- 23. ВАЖНЫЕ ТИПЫ КВАДРАТНЫХ МАТРИЦ
- 24. СВОЙСТВО ЕДИНИЧНОЙ МАТРИЦЫ: A•E=E•A=A
- 25. 2. ОПРЕДЕЛИТЕЛИ
- 26. detA = ОПРЕДЕЛИТЕЛЬ второго порядка
- 27. ОПРЕДЕЛИТЕЛЬ третьего порядка
- 28. Правило Саррюса
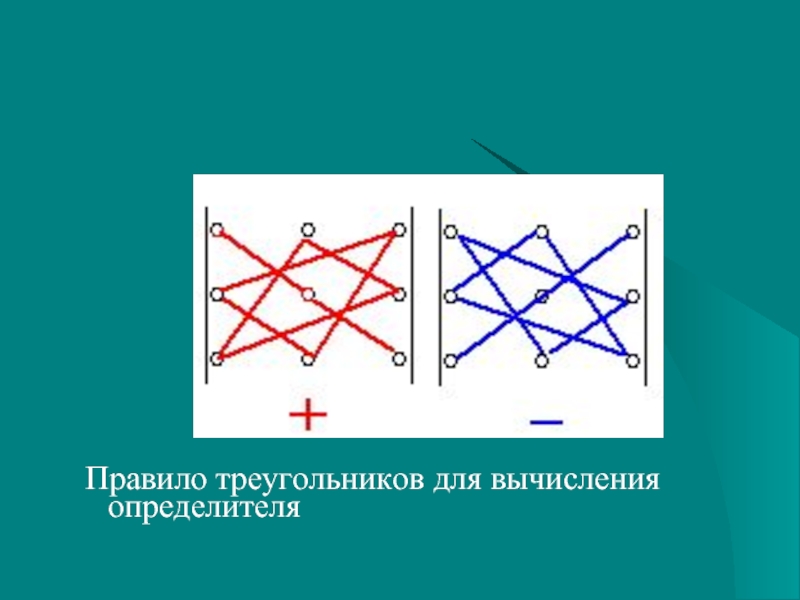
- 29. Правило треугольников для вычисления определителя
- 30. Минор элемента квадратной матрицы .
- 31. Алгебраическое дополнение элемента квадратной матрицы .
- 32. Свойство 1. При транспонировании матрицы ее определитель
- 33. Свойство 7. Определитель с двумя пропорцио-нальными строками
- 34. Свойство 10. Если для элементов какой-либо строки
- 35. Свойство 12. Теорема аннулирования. Сумма произведений элементов
- 36. ВЫРОЖДЕННЫЕ И ОБРАТНЫЕ МАТРИЦЫ
- 37. Если определитель квадратной матрицы А не равен
- 38. Матрица, составленная из алгебраических дополнений элементов исходной
- 39. Обратная матрица .
- 40. Алгоритм вычисления обратной матрицы по формуле (метод присоединенной матрицы) .
- 41. Если матрица не квадратная, то обратной
- 42. Ступенчатая матрица .
- 44. Сводная таблица по векторной алгебре
ПЛАН ЛЕКЦИИ Определение и виды матриц. Действия над матрицами Определители Вырожденные и обратные матрицы Решение систем линейных уравнений
Слайд 1МАТЕМАТИКА.
ТЕМА 1. ЛИНЕЙНАЯ АЛГЕБРА
Лектор:
Карицкая Светлана Геннадьевна,
Кандидат технических наук, доцент
http://connect.ustu.ru
Адрес электронной образовательной
Слайд 2ПЛАН ЛЕКЦИИ
Определение и виды матриц. Действия над матрицами
Определители
Вырожденные и обратные
матрицы
Решение систем линейных уравнений
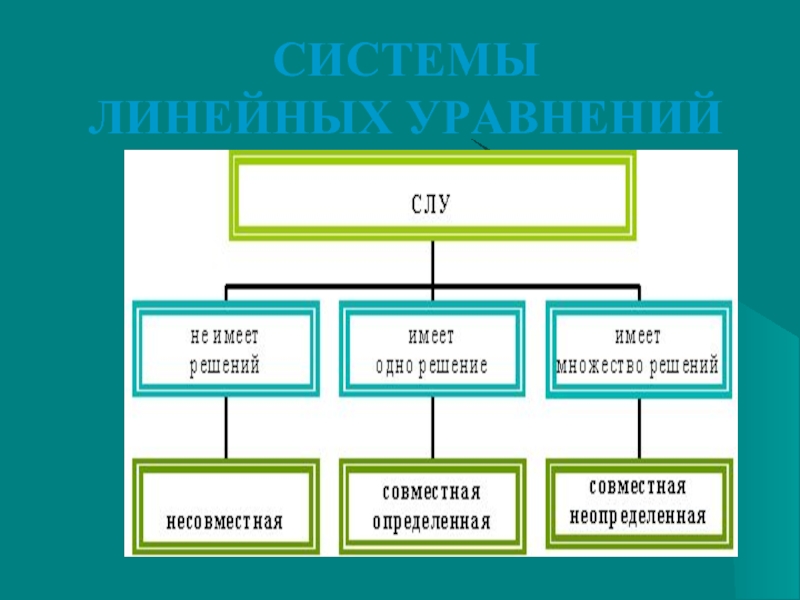
Решение систем линейных уравнений
Слайд 4 ОПРЕДЕЛЕНИЯ
Прямоугольной матрицей размером m×n, где m –
число строк, n – число столбцов, называется прямоугольная таблица чисел, расположенных в определенном порядке. Эти числа называются элементами матрицы. Место каждого элемента однозначно определяется номером строки и столбца, на пересечении которых он находится.
Слайд 6ПРИНЦИП НУМЕРАЦИИ
СТРОК И СТОЛБЦОВ
СТРОКИ НУМЕРУЮТСЯ СВЕРХУ
ВНИЗ, НАЧИНАЯ С №
1.
СТОЛБЦЫ НУМЕРУЮТСЯ СЛЕВА
НАПРАВО, НАЧИНАЯ С № 1.
СТОЛБЦЫ НУМЕРУЮТСЯ СЛЕВА
НАПРАВО, НАЧИНАЯ С № 1.
Слайд 19ВОЗМОЖНОСТЬ УМНОЖЕНИЯ МАТРИЦЫ НА МАТРИЦУ
МАТРИЦУ A, ЗАПИСАННУЮ СЛЕВА, МОЖНО
УМНОЖИТЬ НА
МАТРИЦУ B, ЗАПИСАННУЮ СПРАВА, ТОГДА И ТОЛЬКО ТОГДА, КОГДА ЧИСЛО СТОЛБЦОВ МАТРИЦЫ A РАВНО ЧИСЛУ СТРОК МАТРИЦЫ B
МАТРИЦУ B, ЗАПИСАННУЮ СПРАВА, ТОГДА И ТОЛЬКО ТОГДА, КОГДА ЧИСЛО СТОЛБЦОВ МАТРИЦЫ A РАВНО ЧИСЛУ СТРОК МАТРИЦЫ B
Слайд 20 ПРАВИЛО УМНОЖЕНИЯ МАТРИЦЫ НА МАТРИЦУ КАЖДАЯ СТРОКА ЛЕВОЙ МАТРИЦЫ СКАЛЯРНО УМНОЖАЕТСЯ
НА КАЖДЫЙ СТОЛБЕЦ ПРАВОЙ МАТРИЦЫ
Слайд 32Свойство 1. При транспонировании матрицы ее определитель не меняется:detA = detAT.
Свойство
2. det (A±B) = det A± det B.
Свойство 3. det (AB) = detA⋅detB
Свойство 4. Перестановка любых двух строк (или столбцов) меняет знак определителя.
Свойство 5.Общий множитель строки (столбца) можно выносить за знак определителя.
Свойство 6. Определитель с двумя равными строками (или столбцами) равен нулю.
Свойство 3. det (AB) = detA⋅detB
Свойство 4. Перестановка любых двух строк (или столбцов) меняет знак определителя.
Свойство 5.Общий множитель строки (столбца) можно выносить за знак определителя.
Свойство 6. Определитель с двумя равными строками (или столбцами) равен нулю.
Свойства определителей
.
Слайд 33Свойство 7. Определитель с двумя пропорцио-нальными строками (или столбцами) равен нулю.
Свойство
8. Если матрица содержит нулевой столбец или нулевую строку, то ее определитель равен нулю. (Данное утверждение очевидно, т.к. считать определитель можно именно по нулевой строке или столбцу.)
Свойство 9. Величина определителя не изменится, если к элементам одной из его строк(столбца) прибавить(вычесть) соответствующие элементы другой строки(столбца), умноженные на какое-либо число k, не равное нулю.
Свойство 9. Величина определителя не изменится, если к элементам одной из его строк(столбца) прибавить(вычесть) соответствующие элементы другой строки(столбца), умноженные на какое-либо число k, не равное нулю.
.
Слайд 34Свойство 10. Если для элементов какой-либо строки (или столбца) матрицы верно
соотношение d = d1±d2 , e = e1±e2 , f = f1±f2 , то верно
Свойство 11. Величина определителя треугольной матрицы равна произведению элементов, стоящих на главной диагонали.
Свойство 11. Величина определителя треугольной матрицы равна произведению элементов, стоящих на главной диагонали.
.
Слайд 35Свойство 12. Теорема аннулирования. Сумма произведений элементов некоторой строки (столбца) на
соответствующие алгебраические дополнения элементов другой строки (столбца) равна нулю.
Свойство 13. Теорема разложения. Величина определителя равна сумме произведений элементов некоторой строки (или столбца) на их алгебраические дополнения.
Свойство 13. Теорема разложения. Величина определителя равна сумме произведений элементов некоторой строки (или столбца) на их алгебраические дополнения.
.
Слайд 37Если определитель квадратной матрицы А не равен нулю, матрицу называют невырожденной,
в противном случае А называют вырожденной матрицей.
Вырожденная матрица
.
Слайд 38Матрица, составленная из алгебраических дополнений элементов исходной матрицы А, называется присоединенной
матрицей
.
Слайд 41
Если матрица не квадратная, то обратной матрицы не существует.
Вычисляем определитель исходной
матрицы. Если он равен нулю, обратной матрицы не существует. Если нет, переходим к следующему пункту.
Находим алгебраические дополнения элементов исходной матрицы и составляем из них транспонированную присоединенную матрицу.
Вычисляем обратную матрицу по формуле
Проверяем правильность вычисления обратной матрицы, исходя из ее определения.
Находим алгебраические дополнения элементов исходной матрицы и составляем из них транспонированную присоединенную матрицу.
Вычисляем обратную матрицу по формуле
Проверяем правильность вычисления обратной матрицы, исходя из ее определения.
.
