- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Тригонометрия. Углы презентация
Содержание
- 1. Тригонометрия. Углы
- 2. Выразите угол в радианах с помощью
- 3. Найдите градусную меру угла, радианная мера которого равна: 18° 72° 540° 300° 108°
- 4. у х 0 I
- 5. СИНУС , КОСИНУС, ТАНГЕНС И КОТАНГЕНС УГЛА ИЗ ПРОМЕЖУТКА [0°; 180°]
- 6. ПРОДОЛЖИТЕ ФРАЗУ: Синусом острого угла прямоугольного
- 7. НЕОБХОДИМО ПОНЯТЬ!!! 1. Если существуют
- 8. ПОЛУОКРУЖНОСТЬ С РАДИУСОМ R=1 И ЦЕНТРОМ
- 9. ПРОДОЛЖИТЕ ФРАЗУ: Тангенсом угла называется
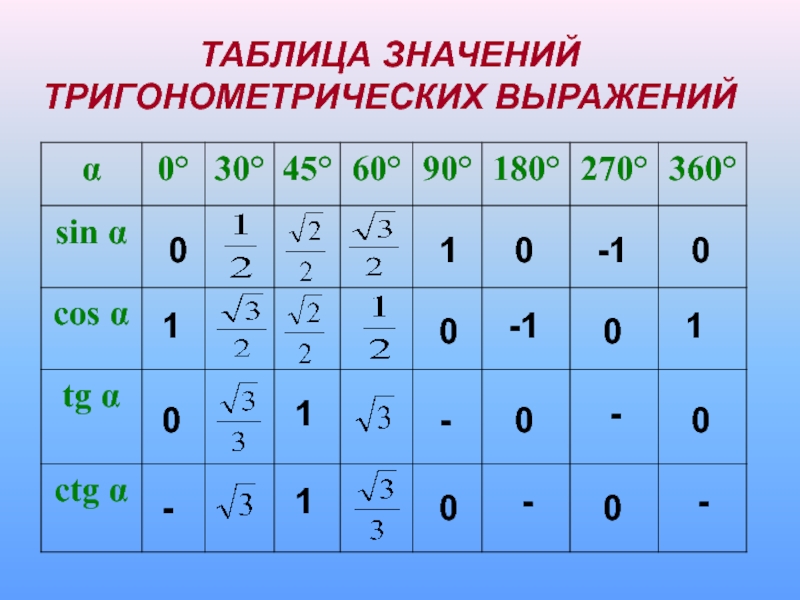
- 10. Вспомним таблицу значений тригонометрических функций углов в
- 11. РАССМОТРИМ УГЛЫ В 0°, 90° И 180°
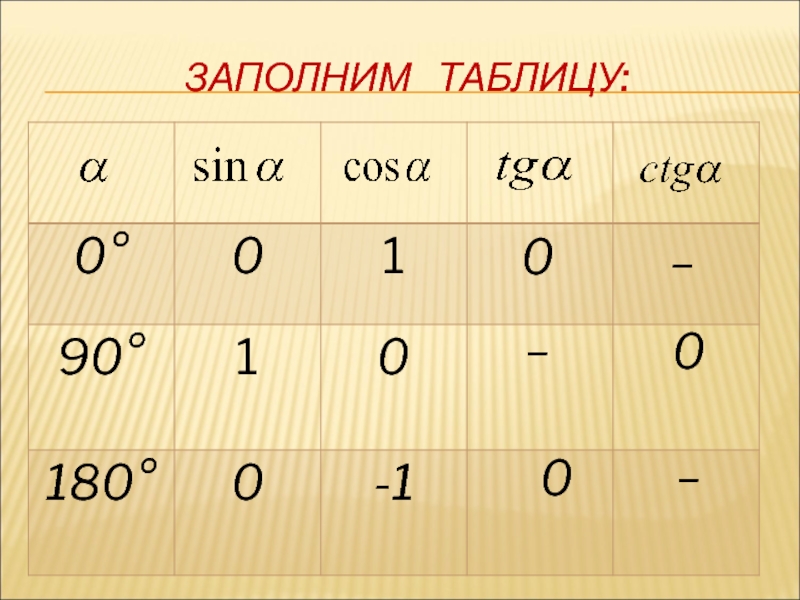
- 12. ЗАПОЛНИМ ТАБЛИЦУ: 0 _ _ 0 0 _
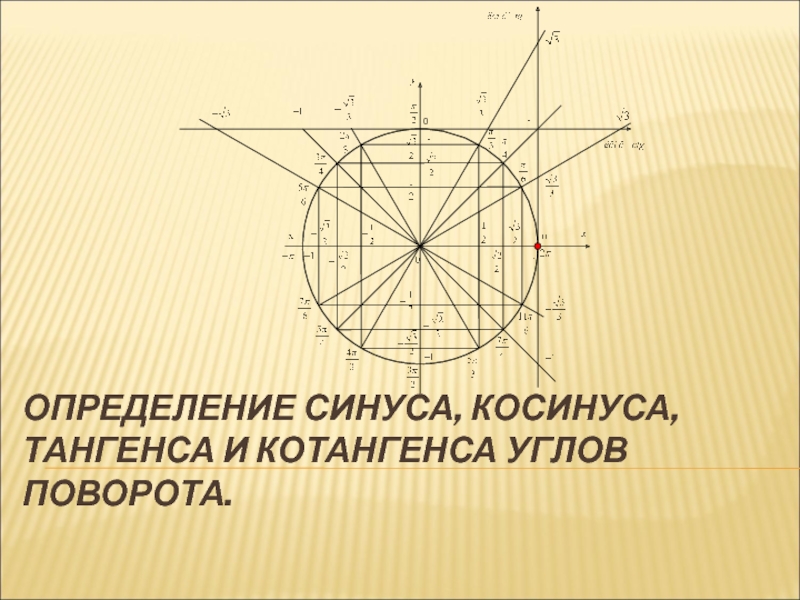
- 13. ОПРЕДЕЛЕНИЕ СИНУСА, КОСИНУСА, ТАНГЕНСА И КОТАНГЕНСА УГЛОВ ПОВОРОТА.
- 14. x y 1 0 1 Вспомним, что
- 15. sinα cosα
- 16. x y 0 1 0 1
- 17. x y 0 1 0 1
- 18. x y 0 1 0 1
- 19. x y 0 1 0 1
- 20. x y 0 1 0 1
- 21. x y 0 1 0 1
- 22. 0 0 0 1 0 -
- 23. 1. «Включите свет» в окнах, т.е. закрасьте
Слайд 4
у
х
0
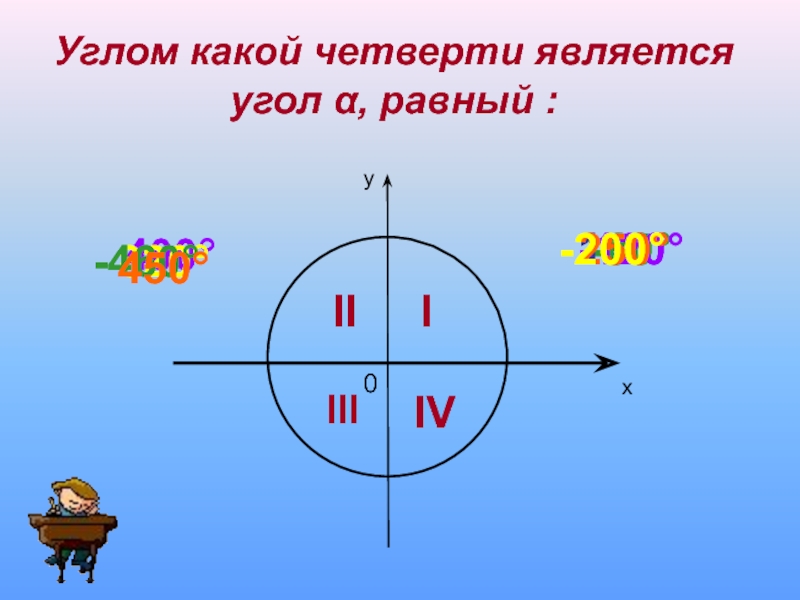
I
II
III
IV
Углом какой четверти является угол α, равный :
45°
-80°
150°
-120°
250°
-200°
400°
820°
-460°
450°
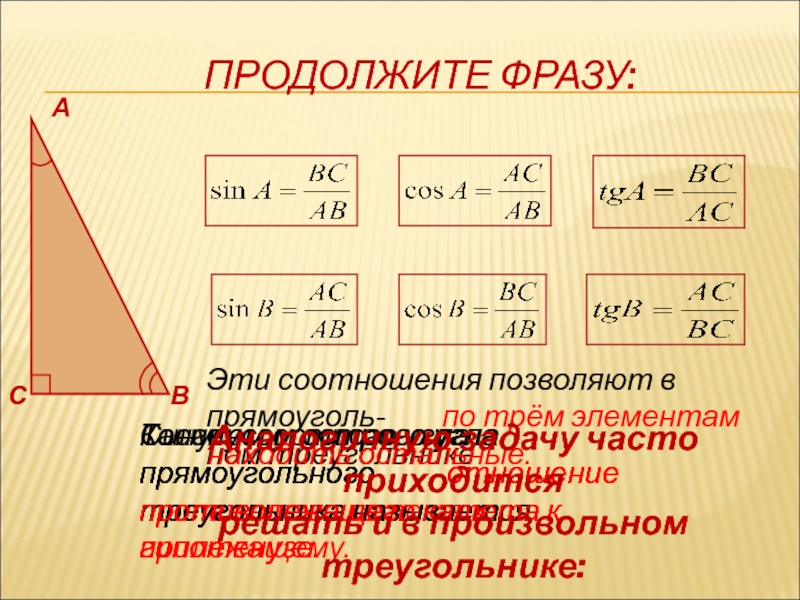
Слайд 6ПРОДОЛЖИТЕ ФРАЗУ:
Синусом острого угла прямоугольного
треугольника называется
А
С
В
противолежащего катета к гипотенузе.
Косинусом острого угла прямоугольного
треугольника называется
отношение
прилежащего катета к гипотенузе.
Тангенсом острого угла прямоугольного
треугольника называется
отношение
противолежащего катета к прилежащему.
Эти соотношения позволяют в прямоуголь-
ном треугольнике
по трём элементам
находить остальные.
Аналогичную задачу часто приходится
решать и в произвольном треугольнике:
остороугольном и тупоугольном.
Слайд 7НЕОБХОДИМО ПОНЯТЬ!!!
1. Если существуют соотношения между сторонами и углами в произвольном
2. Если существуют соотношения между сторонами и углами в произвольном треугольнике, то каковы эти соотношения?
Слайд 8 ПОЛУОКРУЖНОСТЬ С РАДИУСОМ R=1 И ЦЕНТРОМ В НАЧАЛЕ КООРДИНАТ НАЗЫВАЕТСЯ
М(х;у)
х
у
О
В треугольнике МОХ
sin =
=
=у
cos =
=
=х
y=sin
x=cos
Если точка М лежит
на единичной полу-
окружности под углом
к положительной полу-
оси ОХ,то sin назы-
вается ордината у
точки М, а сos - абс-
цисса х этой точки.
0°< <90°
90°< <180°
Слайд 9ПРОДОЛЖИТЕ ФРАЗУ:
Тангенсом угла
называется
отношение ординаты
точки на единичной
полуокружности к
абсциссе или отношение
синуса угла к его косинусу.
М(х;у)
х
у
Котангенсом угла
называется
отношение абсциссы
точки на единичной
полуокружности к её
ординате или отношение
косинуса угла к его синусу.
Слайд 10Вспомним таблицу значений тригонометрических функций углов в 30º, 45º, 60º.
30º
60º
45º
α
sin
α
α
α
α
cos
tg
ctg
1
2
3
1
1
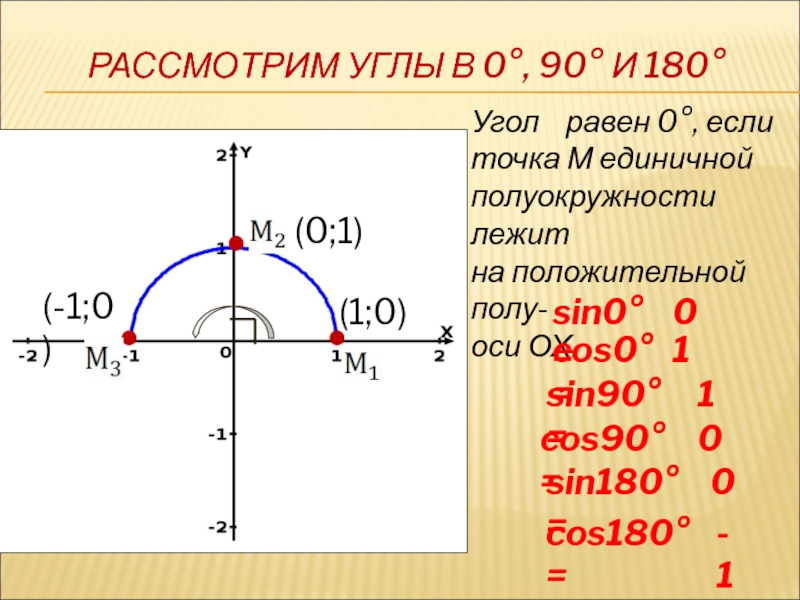
Слайд 11РАССМОТРИМ УГЛЫ В 0°, 90° И 180°
(1;0)
(-1;0)
(0;1)
Угол
точка М единичной
полуокружности лежит
на положительной полу-
оси ОХ.
sin0°=
cos0°=
sin90°=
sin180°=
cos90°=
cos180°=
0
1
1
0
0
-1
Слайд 14x
y
1
0
1
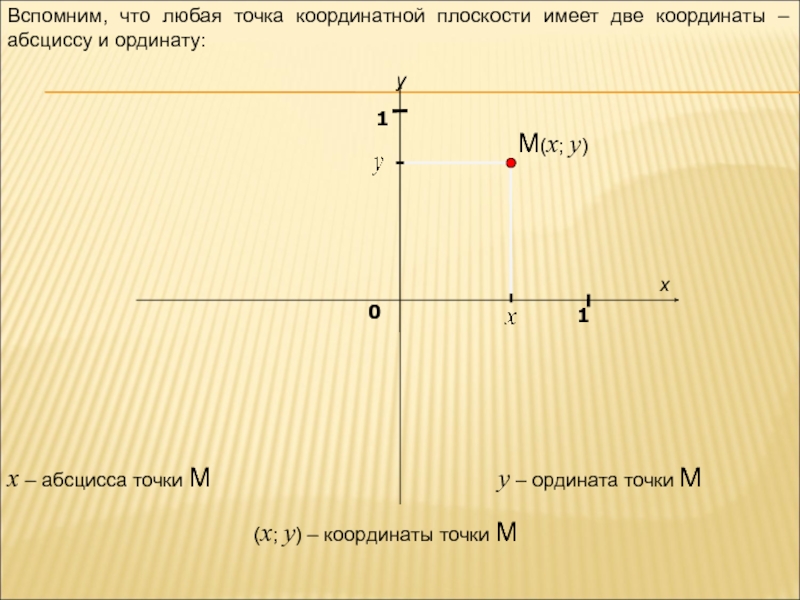
Вспомним, что любая точка координатной плоскости имеет две координаты – абсциссу
y – ордината точки M
x – абсцисса точки M
M(x; y)
(x; y) – координаты точки M
Слайд 15
sinα
cosα
α
x
y
0
1
0
1
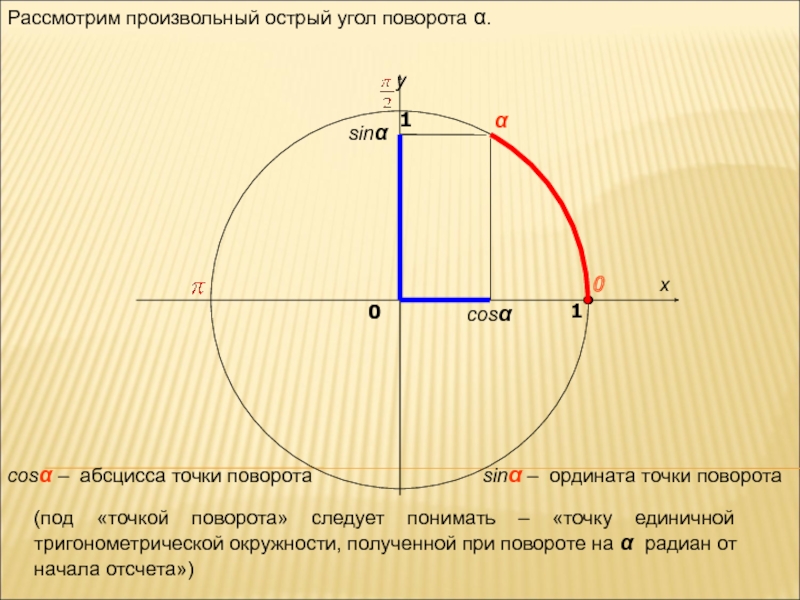
sinα – ордината точки поворота
cosα – абсцисса точки поворота
(под «точкой
Рассмотрим произвольный острый угол поворота α.
Слайд 16
x
y
0
1
0
1
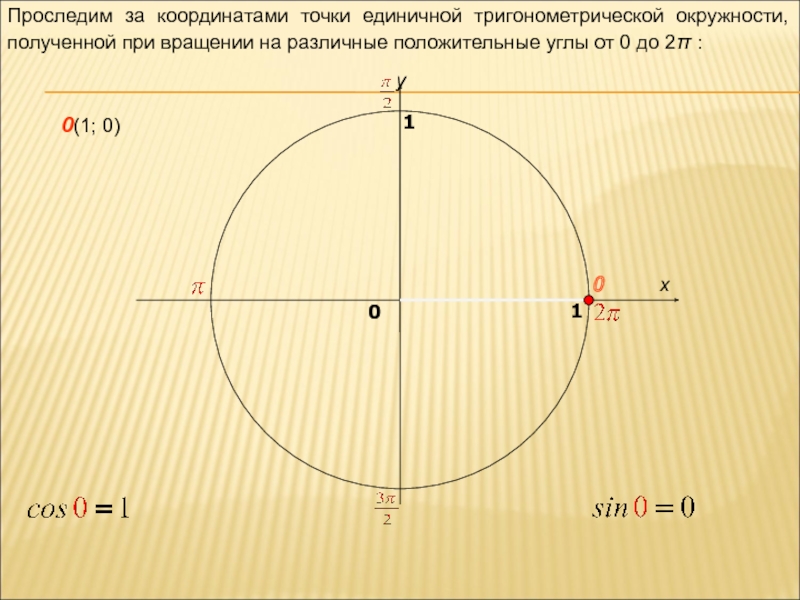
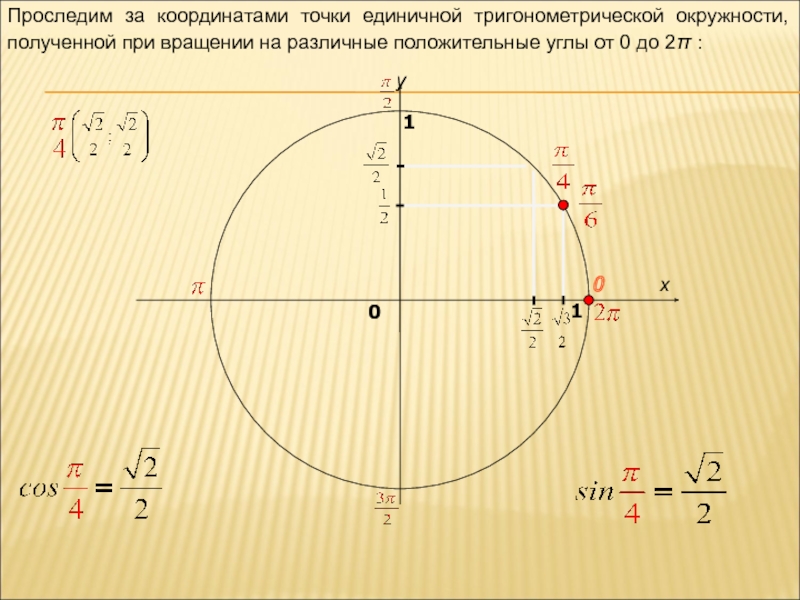
Проследим за координатами точки единичной тригонометрической окружности, полученной при вращении на
0(1; 0)
Слайд 17
x
y
0
1
0
1
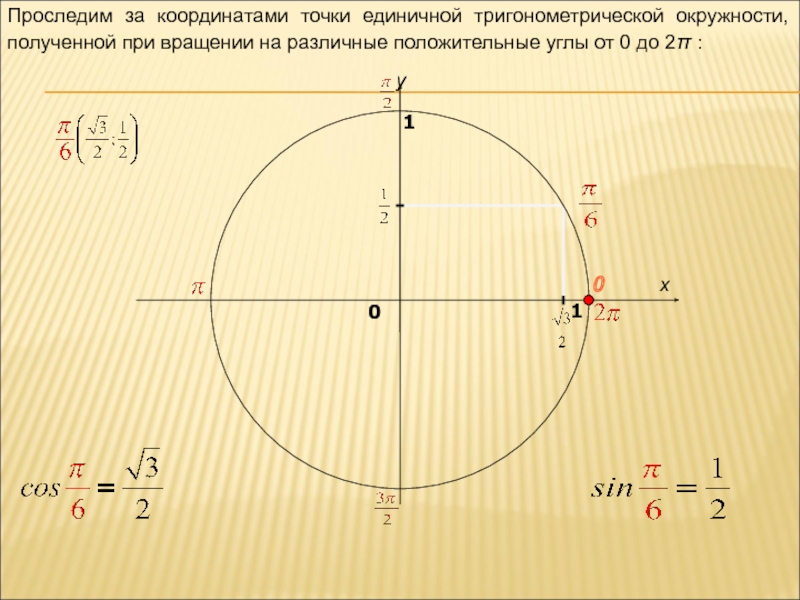
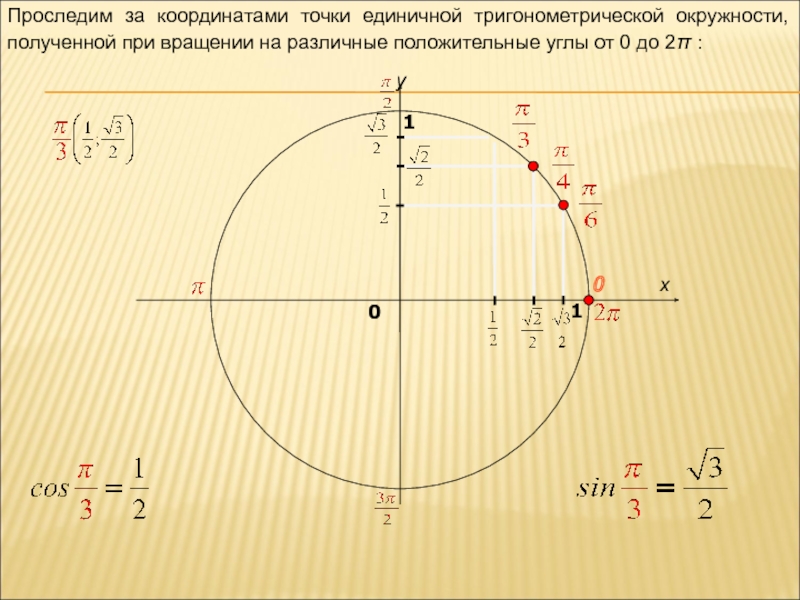
Проследим за координатами точки единичной тригонометрической окружности, полученной при вращении на
Слайд 18
x
y
0
1
0
1
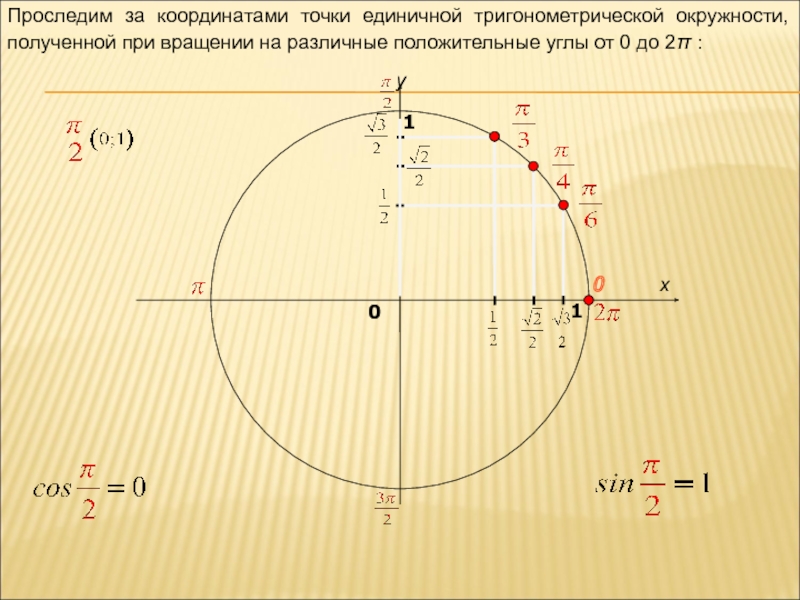
Проследим за координатами точки единичной тригонометрической окружности, полученной при вращении на
Слайд 19
x
y
0
1
0
1
Проследим за координатами точки единичной тригонометрической окружности, полученной при вращении на
Слайд 20
x
y
0
1
0
1
Проследим за координатами точки единичной тригонометрической окружности, полученной при вращении на
Слайд 21
x
y
0
1
0
1
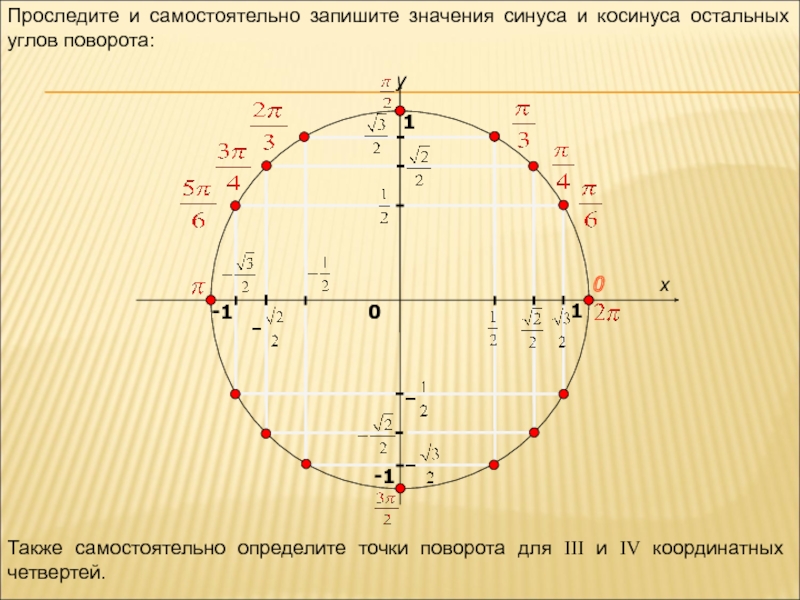
Проследите и самостоятельно запишите значения синуса и косинуса остальных углов поворота:
-1
-1
Также
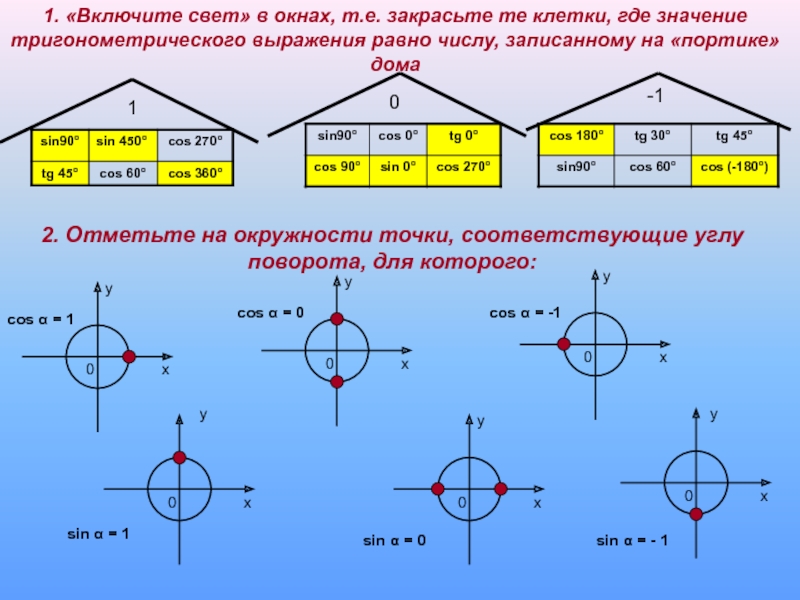
Слайд 231. «Включите свет» в окнах, т.е. закрасьте те клетки, где значение
0
1
-1
2. Отметьте на окружности точки, соответствующие углу поворота, для которого:
у
х
0
у
х
0
у
х
0
у
х
0
у
х
0
у
х
0
cos α = 1
cos α = 0
cos α = -1
sin α = 1
sin α = - 1
sin α = 0



![СИНУС , КОСИНУС, ТАНГЕНС И КОТАНГЕНС УГЛА ИЗ ПРОМЕЖУТКА [0°; 180°]](/img/tmb/1/37751/0f8e8432daa6bb8fce02dbf454ef5d79-800x.jpg)