- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Треугольники. Виды треугольников. Признаки равенства треугольников презентация
Содержание
- 1. Треугольники. Виды треугольников. Признаки равенства треугольников
- 2. Треугольником называется фигура, которая состоит из
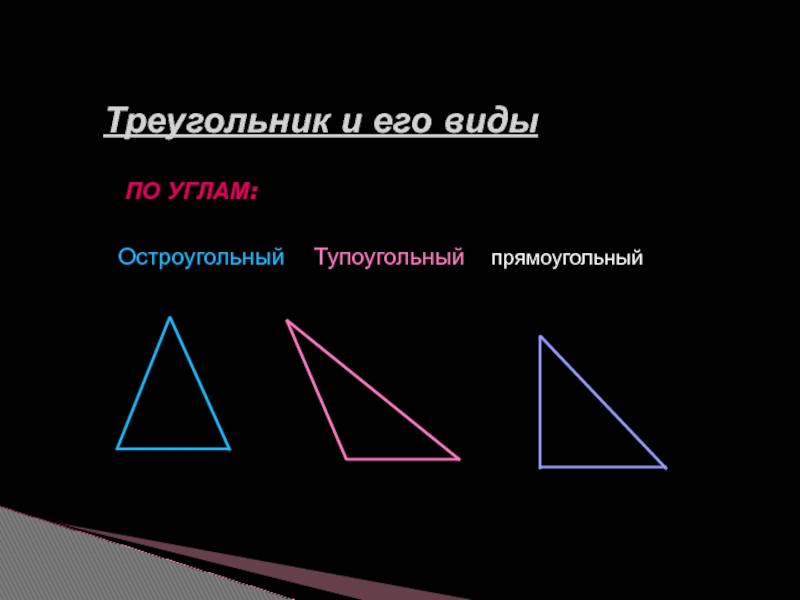
- 3. ПО УГЛАМ: Остроугольный Тупоугольный прямоугольный Треугольник и его виды
- 4. ПО СТОРОНАМ: Разносторонний равнобедренный равносторонний Треугольник и его виды
- 5. Медиана-отрезок, соединяющий вершину треугольника с серединой
- 6. Биссектриса-отрезок биссектрисы угла треугольника, соединяющий вершину
- 7. Треугольник и его элементы. Высота-
- 8. Первый признак: Если
- 9. Второй признак: Если
- 10. Третий признак: Если
- 11. Треугольник называется равнобедренным, если у него
- 12. В равнобедренном треугольнике углы при основании равны,
- 13. Если в треугольнике два угла равны, то
- 14. Треугольник называется равносторонним, если у
- 15. В равностороннем треугольнике все углы равны. В
- 17. Уже
- 18. То, что углы при
- 19. Эвклид Эйлер Архимед
- 20. Герон
- 21. СПАСИБО ЗА ВНИМАНИЕ!!!!!!!
Слайд 2 Треугольником называется фигура, которая состоит из трех точек, не лежащих
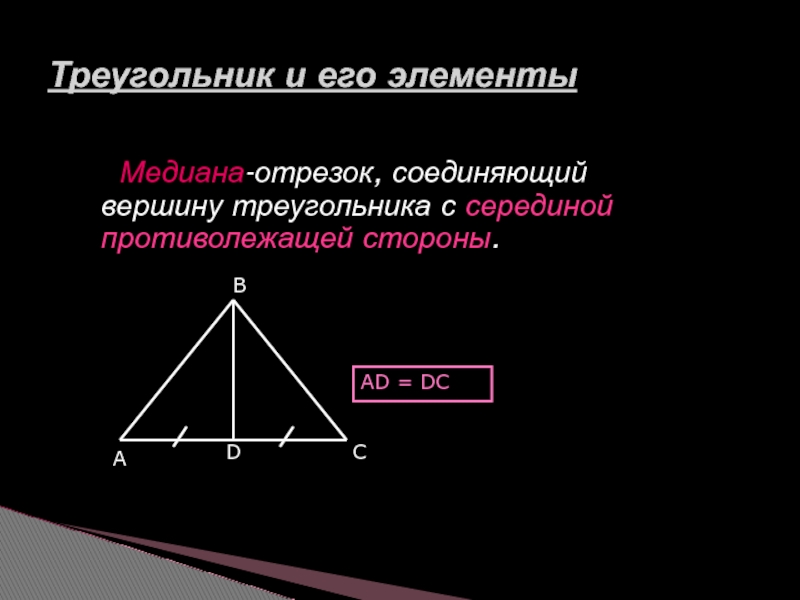
Слайд 5 Медиана-отрезок, соединяющий вершину треугольника с серединой противолежащей стороны.
Треугольник и его
A
C
B
D
АD = DC
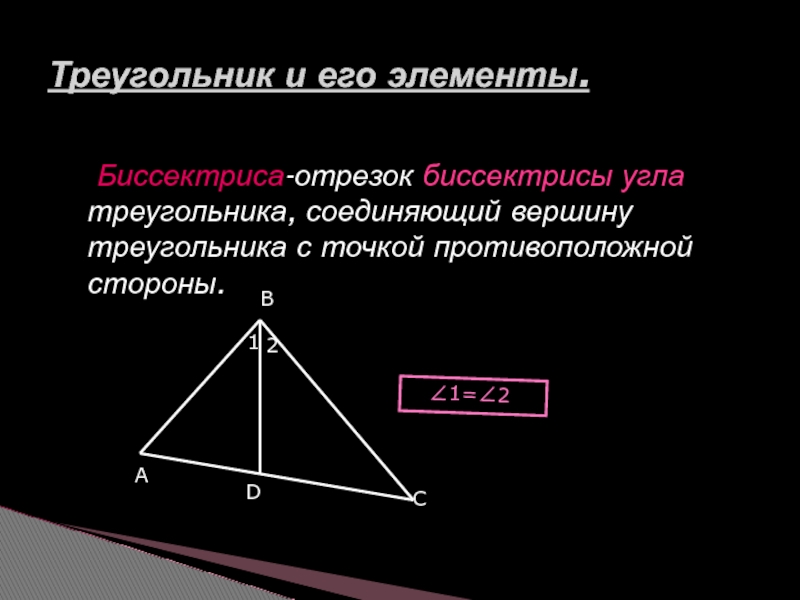
Слайд 6 Биссектриса-отрезок биссектрисы угла треугольника, соединяющий вершину треугольника с точкой противоположной
Треугольник и его элементы.
1
2
∠1=∠2
A
B
C
D
Слайд 7
Треугольник и его элементы.
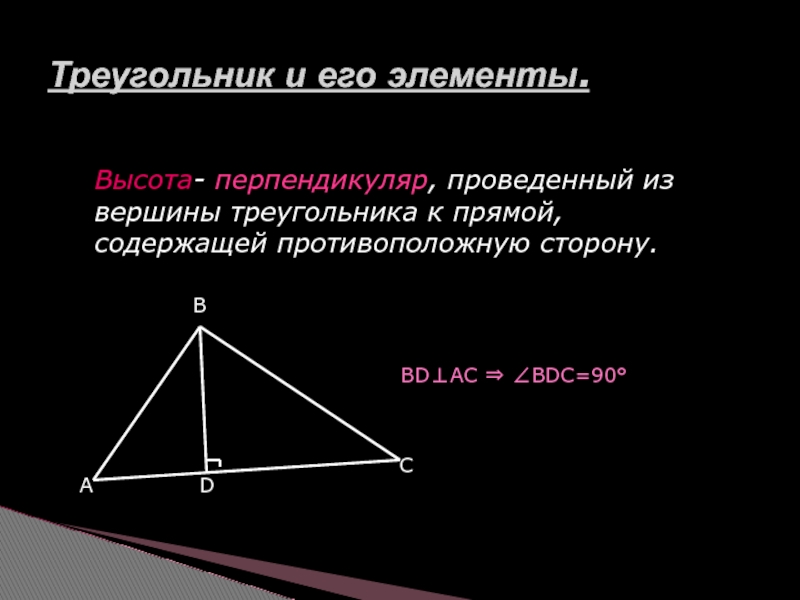
Высота- перпендикуляр, проведенный из вершины треугольника к прямой,
ВD⊥АС ⇒ ∠ВDС=90°
A
B
C
D
Слайд 8 Первый признак:
Если две стороны и угол между
одного треугольника равны соответственно двум сторонам и углу между ними другого треугольника, то такие треугольники равны.
Признаки равенства треугольников
Слайд 9 Второй признак:
Если сторона и два прилежащих к
Признаки равенства треугольников
Слайд 10 Третий признак:
Если три стороны одного треугольника равны
Признаки равенства треугольников
Слайд 11 Треугольник называется равнобедренным, если у него две стороны равны.
АС=СВ
АВ- основание
Определение равнобедренного треугольника.
A
B
C
Слайд 12В равнобедренном треугольнике углы при основании равны, а биссектриса, проведённая к
Свойства равнобедренного треугольника
ΔАВС- равнобедренный ⇒ ∠А=∠В, СD- биссектриса, медиана и высота
A
B
D
C
Слайд 13Если в треугольнике два угла равны, то он равнобедренный.
Если в треугольнике
Если в треугольнике медиана является биссектрисой, то он равнобедренный.
Если в треугольнике высота является биссектрисой, то он равнобедренный.
Признаки равнобедренного треугольника
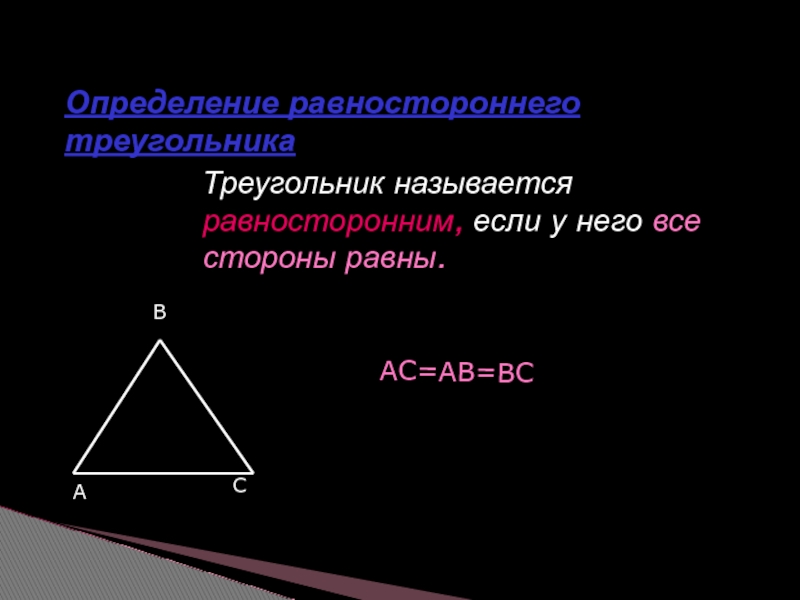
Слайд 14 Треугольник называется равносторонним, если у него все стороны
Определение равностороннего треугольника
АС=АВ=ВС
A
B
C
Слайд 15В равностороннем треугольнике все углы равны.
В равностороннем треугольнике каждая биссектриса является
В равностороннем треугольнике все три медианы равны.
Свойства равностороннего треугольника
Слайд 16
Треугольник – самая простая
Исторические сведения
Слайд 17 Уже Фалес доказал, что треугольник
Понятие о треугольнике исторически развивалось так: сначала рассматривались лишь равносторонние, затем равнобедренные и, наконец, разносторонние треугольники. Равнобедренный треугольник обладает рядом геометрических свойств, которые привлекли к себе внимание еще в древности. В задачах на треугольники, содержащихся в папирусе Ахмеса, на первый план выступают равнобедренный и прямоугольный треугольники. На практике часто применялось свойство медианы равнобедренного треугольника, являющейся одновременно и высотой и биссектрисой.
Слайд 18 То, что углы при основании равнобедренного треугольника равны,
Красивые теоремы о треугольнике доказывали замечательные ученые древности, как Аполлоний, Герон, Менелай и Птолемей. Закономерность в расположении трех замечательных точек треугольника - центра описанной окружности, центроида и ортоцента - впервые обнаружил знаменитый математик Леонард Эйлер.
Свойство суммы углов треугольника было установлено еще в Древнем Египте. Доказательство, изложенное в современных учебниках, содержится в комментарии
Прокла к “Началам” Евклида. Прокл утверждает, что это доказательство было открыто еще пифагорейцами в V веке до н.э. В первой книге “Начал” Евклид излагает другое доказательство теоремы о сумме углов треугольника.