- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Треугольник. Виды треугольников презентация
Содержание
- 1. Треугольник. Виды треугольников
- 2. Треугольник простейший многоугольник, имеющий 3 вершины (угла)
- 3. Виды треугольников по сторонам Равносторонний Равнобедренный Разносторонний
- 4. Виды треугольников по углам Прямоугольный Тупоугольный
- 5. Свойства медиан треугольника: 1. Медианы треугольника
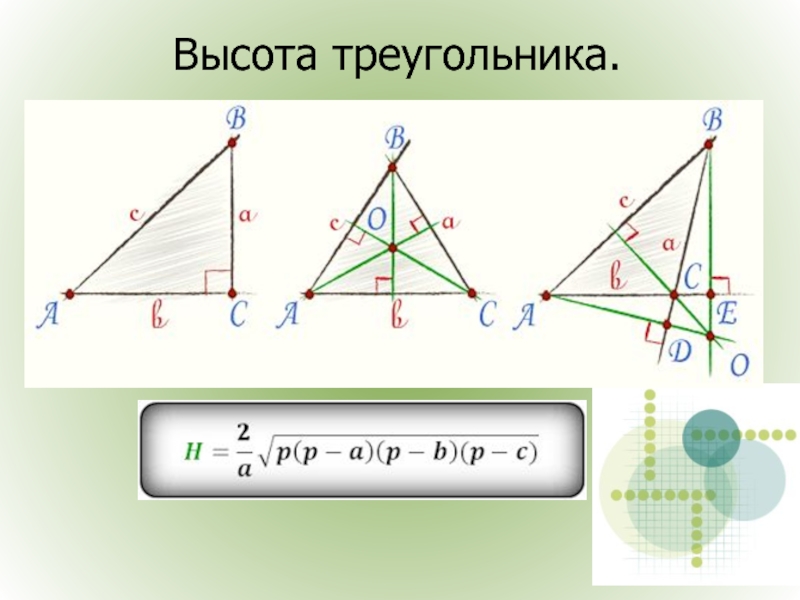
- 6. Высота треугольника.
- 7. Биссектриса треугольника. Свойства биссектрис треугольника: 1. Биссектриса
- 8. Средняя линия Средней линией треугольника называется отрезок, соединяющий
- 9. 2. Средняя линия треугольника отсекает от
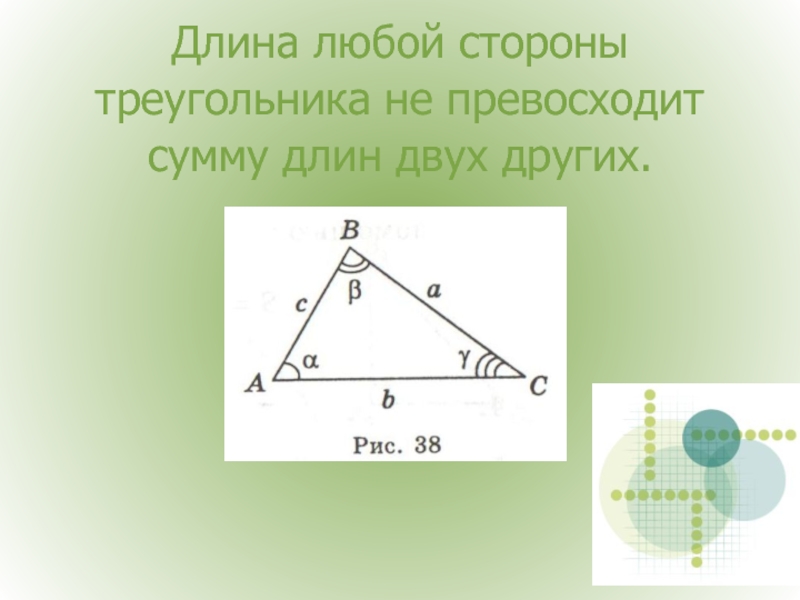
- 10. Длина любой стороны треугольника не превосходит сумму длин двух других.
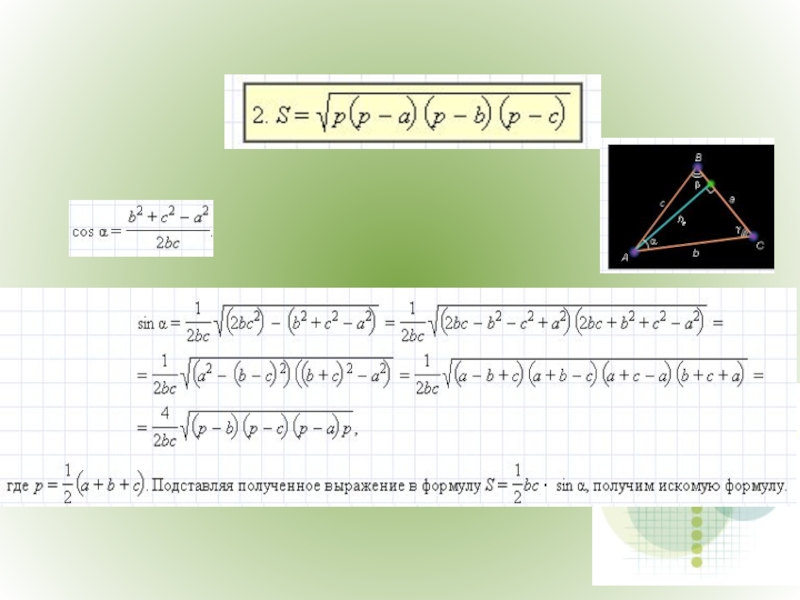
- 11. Площадь треугольника.
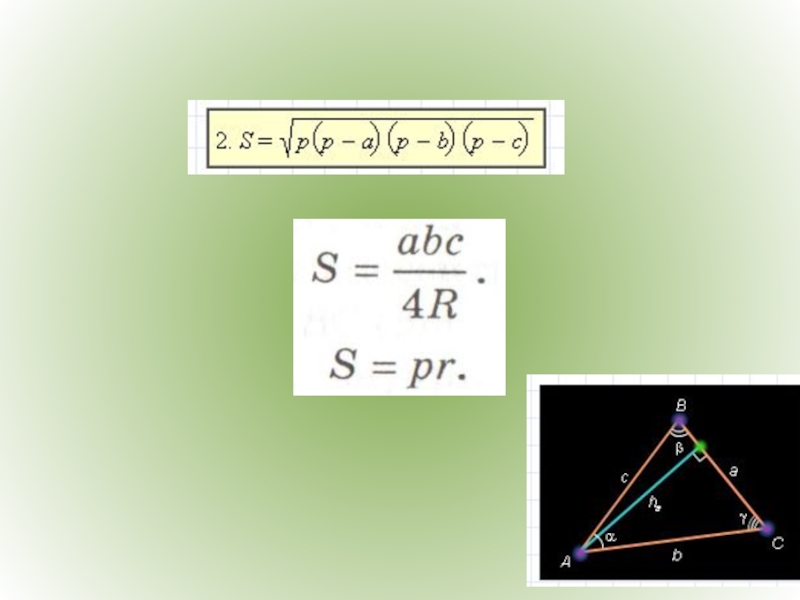
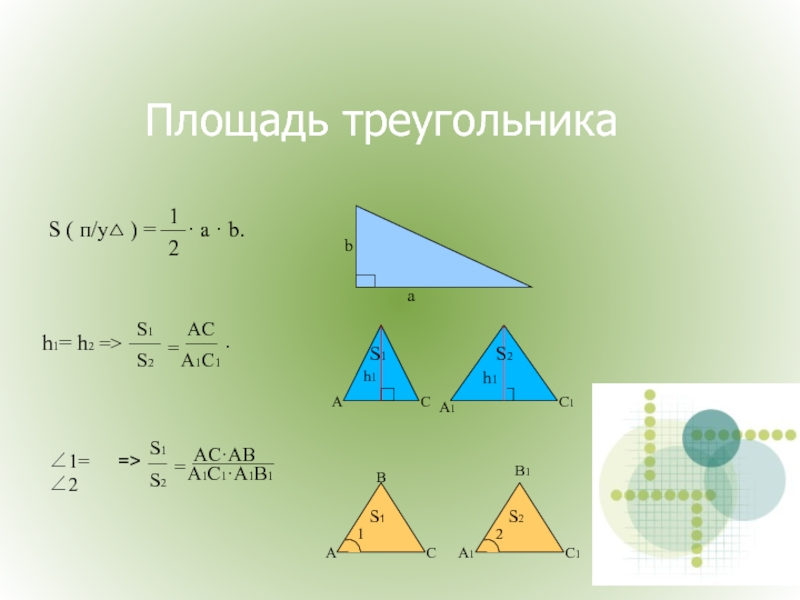
- 15. Площадь треугольника
- 16. Равенство треугольников Признаки равенства треугольников: 2.
- 17. Подобие треугольников Признаки подобия треугольников: 1.
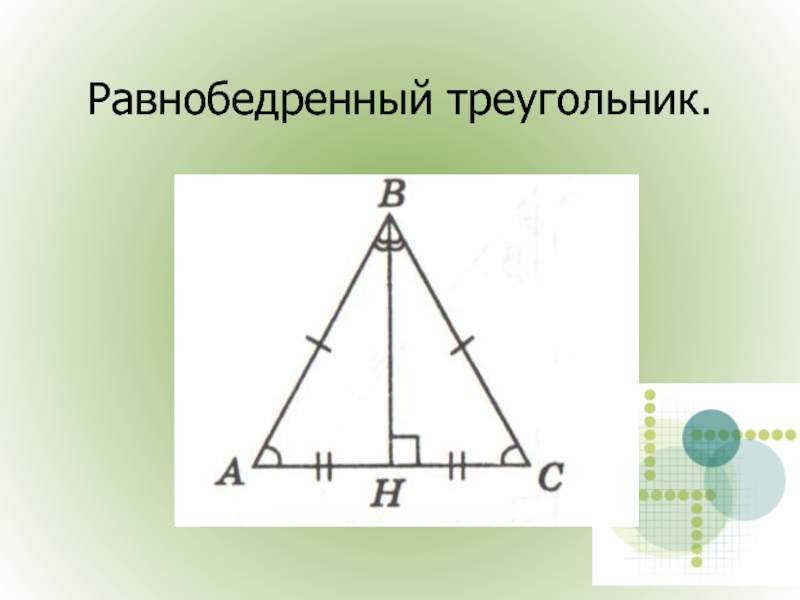
- 18. Равнобедренный треугольник.
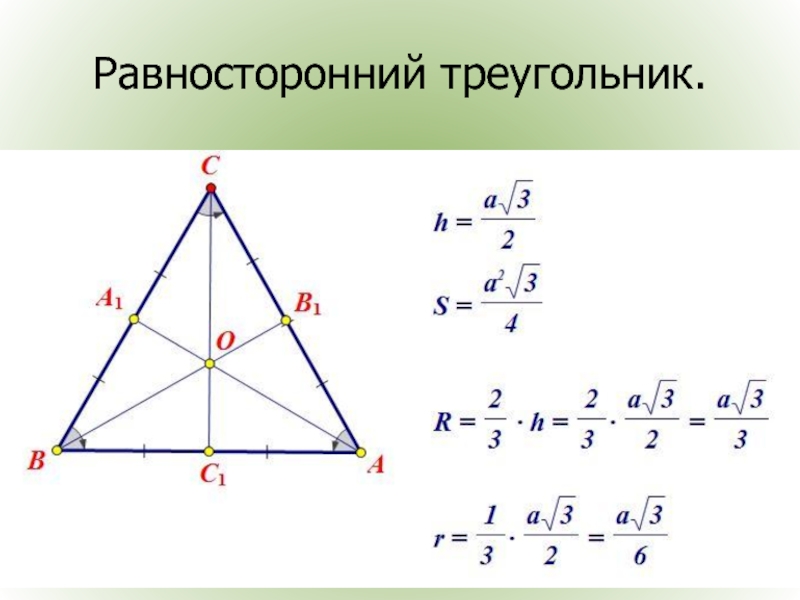
- 19. Равносторонний треугольник.
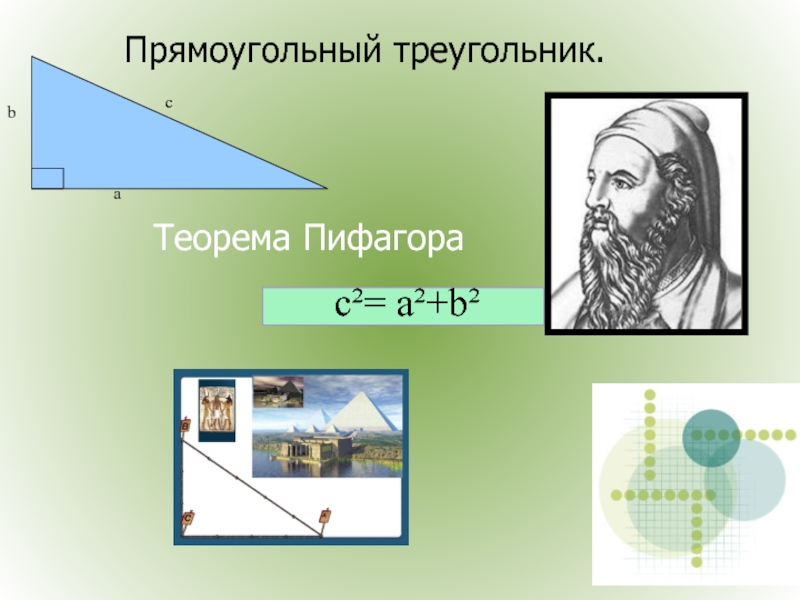
- 20. Теорема Пифагора c²= а²+b² Прямоугольный треугольник.
- 21. Доказательство теоремы Пифагора Дано: а,b- катеты, с-гипотенуза.
- 22. Задача Вот
- 23. Признаки равенства прямоугольных треугольников. Признак
- 24. Свойства прямоугольного треугольника 1. Сумма острых углов прямоугольного
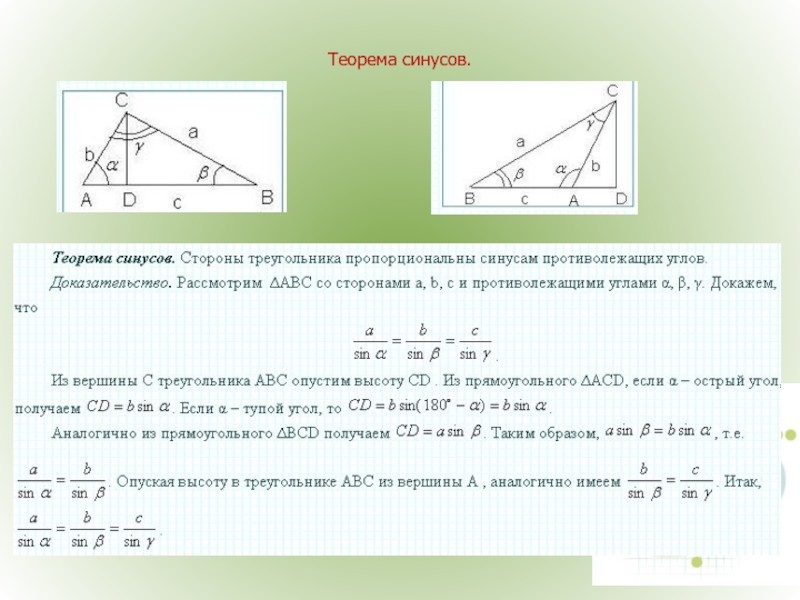
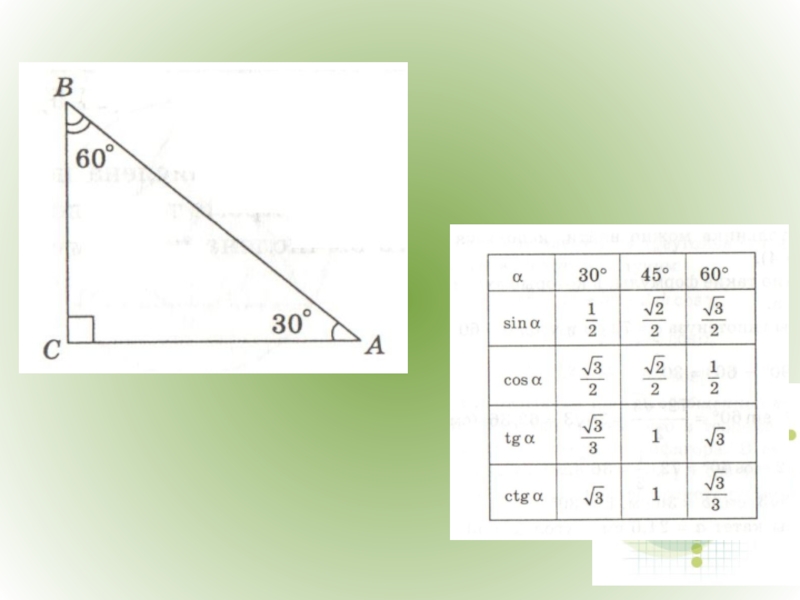
- 25. Теорема синусов.
- 26. Теорема косинусов.
- 27. Задача
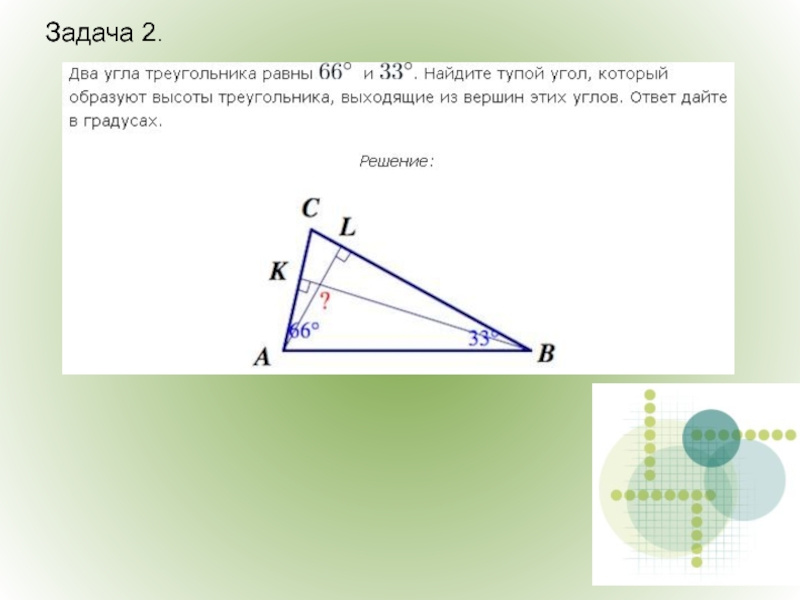
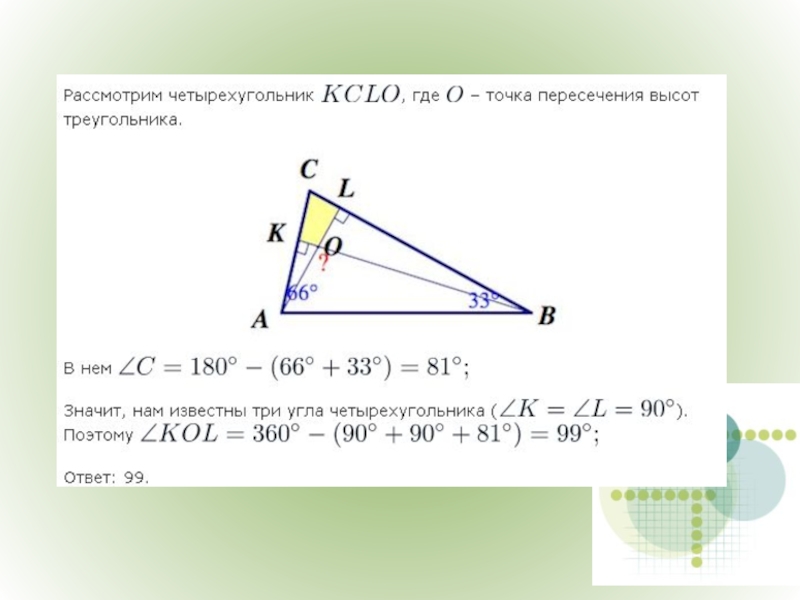
- 39. Задача 2.
- 41. Спасибо за внимание!
Треугольник простейший многоугольник, имеющий 3 вершины (угла) и 3 стороны; часть плоскости, ограниченная тремя точками, и тремя отрезками, попарно соединяющими эти точки; замкнутая ломаная линия с тремя звеньями.
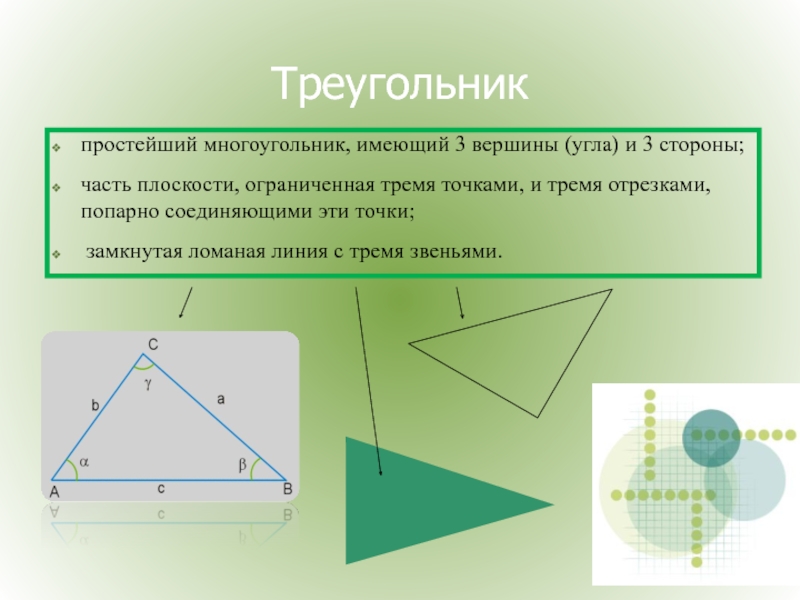
Слайд 2Треугольник
простейший многоугольник, имеющий 3 вершины (угла) и 3 стороны;
часть плоскости,
ограниченная тремя точками, и тремя отрезками, попарно соединяющими эти точки;
замкнутая ломаная линия с тремя звеньями.
замкнутая ломаная линия с тремя звеньями.
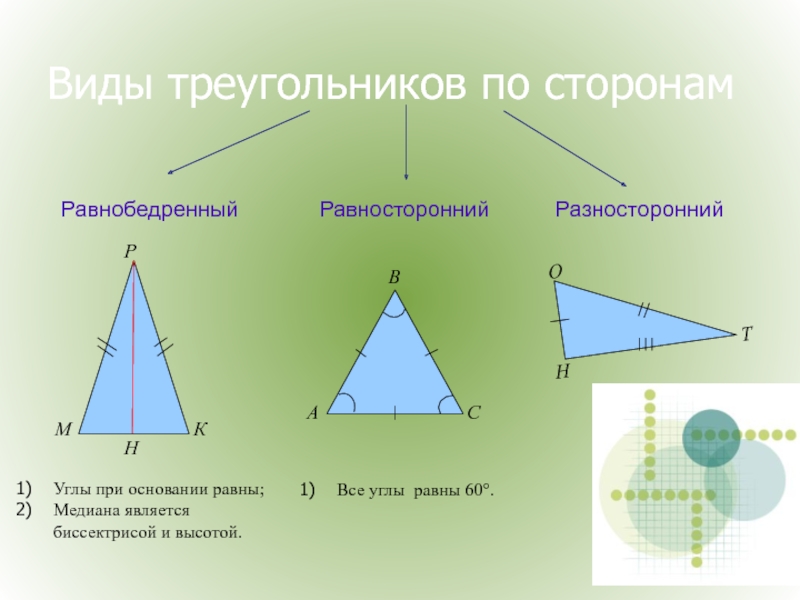
Слайд 3Виды треугольников по сторонам
Равносторонний
Равнобедренный
Разносторонний
Углы при основании равны;
Медиана является биссектрисой и высотой.
Все
углы равны 60°.
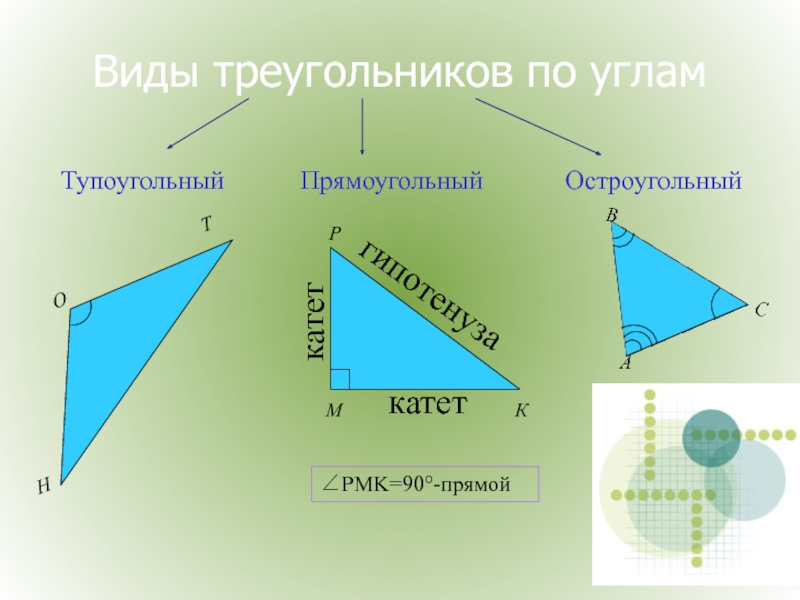
Слайд 4Виды треугольников по углам
Прямоугольный
Тупоугольный
Н
О
Т
Остроугольный
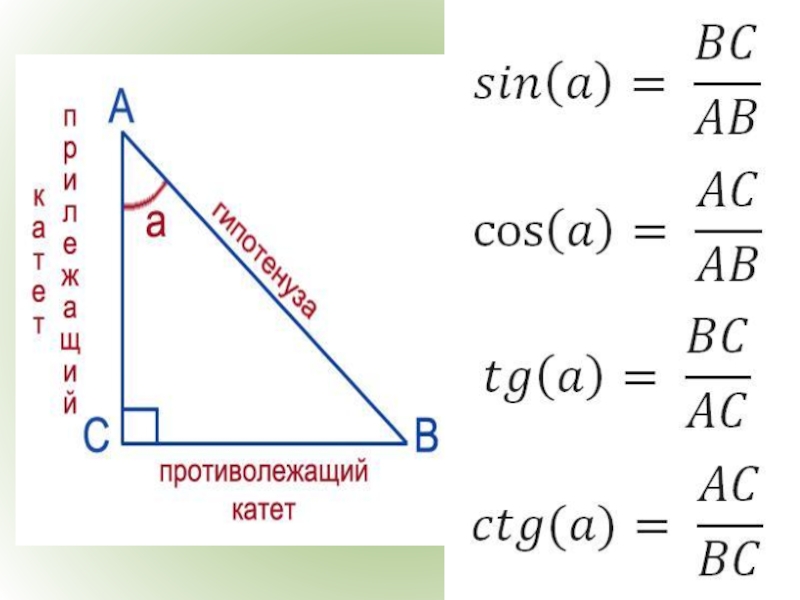
катет
катет
гипотенуза
∠PMK=90°-прямой
Слайд 5
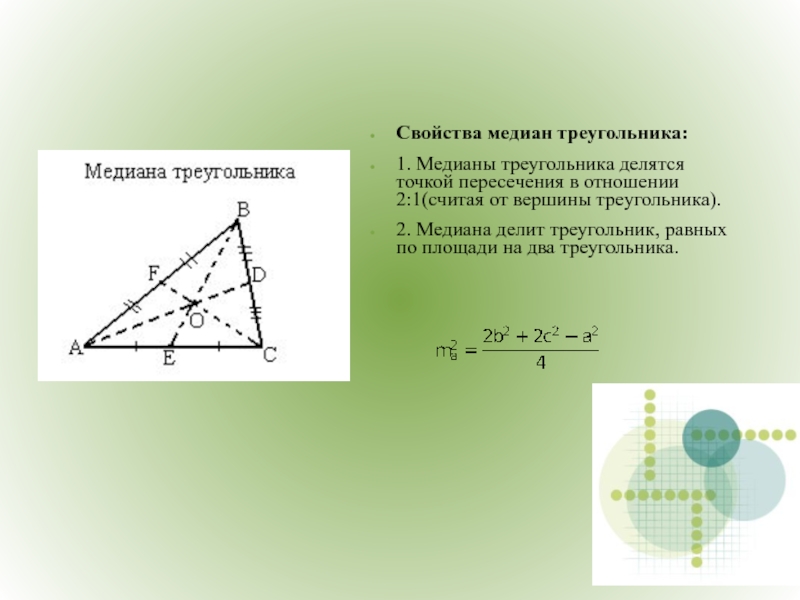
Свойства медиан треугольника:
1. Медианы треугольника делятся точкой пересечения в отношении 2:1(считая
от вершины треугольника).
2. Медиана делит треугольник, равных по площади на два треугольника.
2. Медиана делит треугольник, равных по площади на два треугольника.
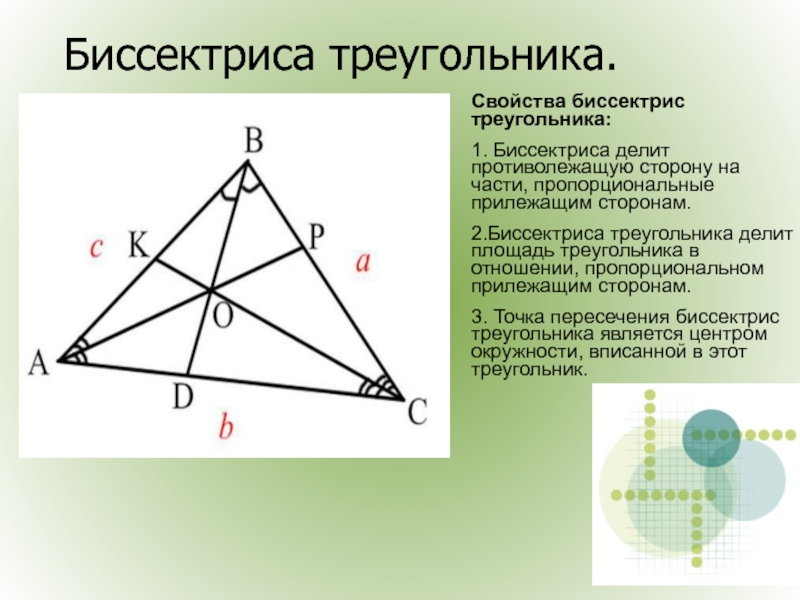
Слайд 7Биссектриса треугольника.
Свойства биссектрис треугольника:
1. Биссектриса делит противолежащую сторону на части, пропорциональные
прилежащим сторонам.
2.Биссектриса треугольника делит площадь треугольника в отношении, пропорциональном прилежащим сторонам.
3. Точка пересечения биссектрис треугольника является центром окружности, вписанной в этот треугольник.
2.Биссектриса треугольника делит площадь треугольника в отношении, пропорциональном прилежащим сторонам.
3. Точка пересечения биссектрис треугольника является центром окружности, вписанной в этот треугольник.
Слайд 8Средняя линия
Средней линией треугольника называется отрезок, соединяющий середины двух его сторон.
Свойство средней
линии треугольника
Средняя линия треугольника параллельна одной из его сторон и равна половине этой стороны.
Средняя линия треугольника параллельна одной из его сторон и равна половине этой стороны.
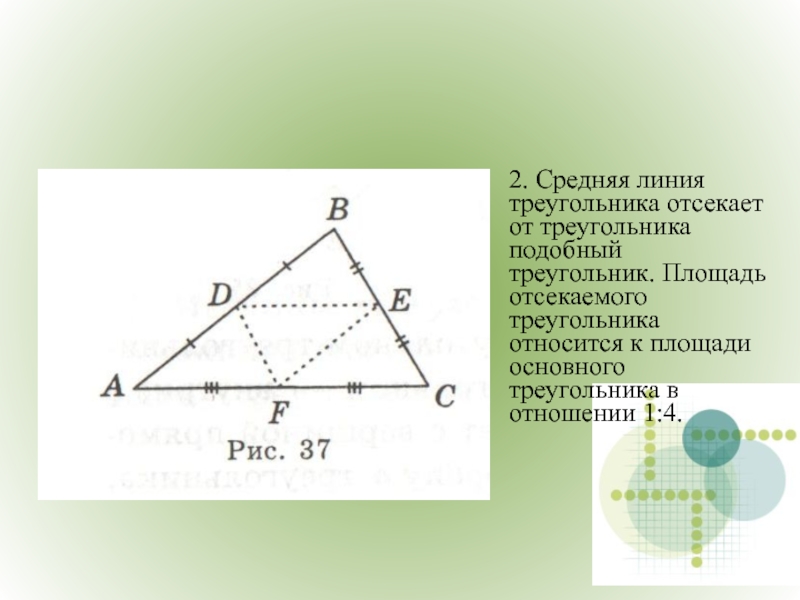
Слайд 9
2. Средняя линия треугольника отсекает от треугольника подобный треугольник. Площадь отсекаемого
треугольника относится к площади основного треугольника в отношении 1:4.
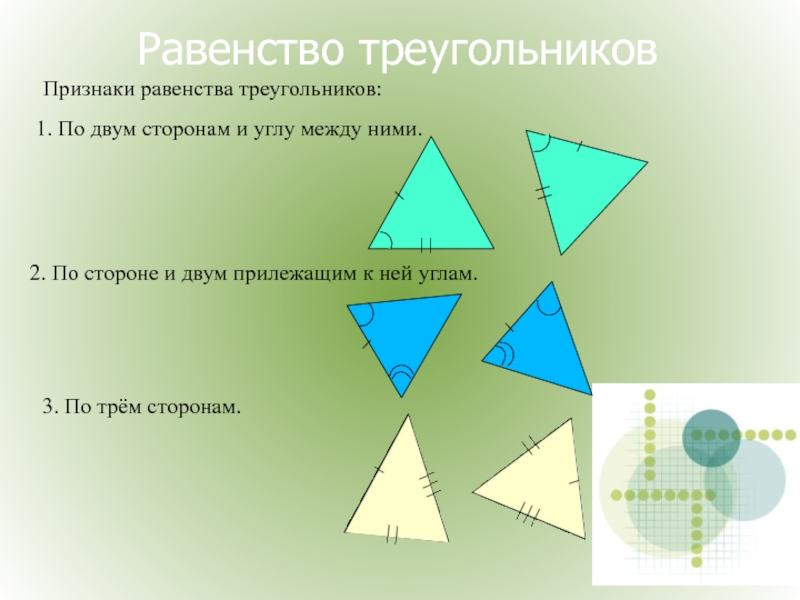
Слайд 16Равенство треугольников
Признаки равенства треугольников:
2. По стороне и двум прилежащим к ней
углам.
3. По трём сторонам.
1. По двум сторонам и углу между ними.
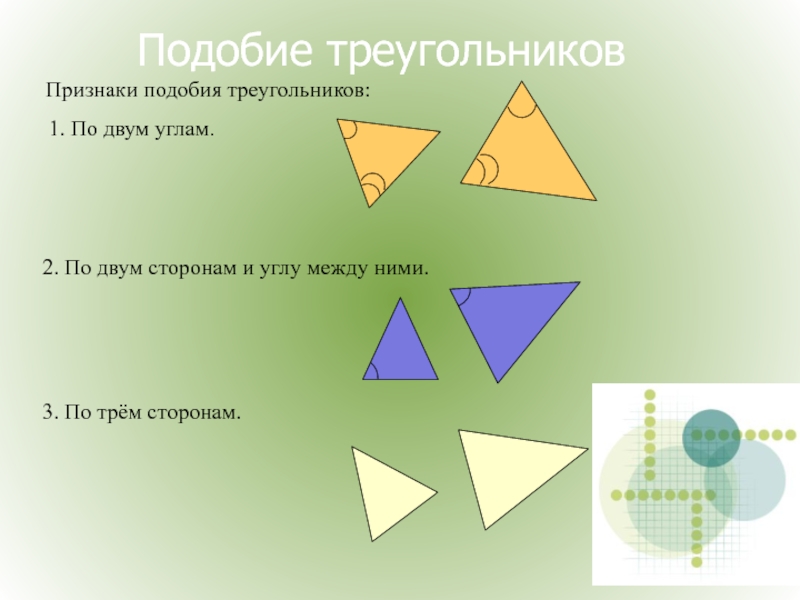
Слайд 17Подобие треугольников
Признаки подобия треугольников:
1. По двум углам.
2. По двум сторонам и
углу между ними.
3. По трём сторонам.
Слайд 21Доказательство теоремы Пифагора
Дано: а,b- катеты, с-гипотенуза.
Доказать: a2+b2=c2.
Доказательство:
Достроим до квадрата со
стороной (a+b).
S1=(a+b)2
S2=4(1/2ab)+c2
Приравняем площади:S1=S2.
(a+b)2=4(1/2ab)+c2
а2+2ab+b2=2ab+c2
а2+b2=c2
S1=(a+b)2
S2=4(1/2ab)+c2
Приравняем площади:S1=S2.
(a+b)2=4(1/2ab)+c2
а2+2ab+b2=2ab+c2
а2+b2=c2
Слайд 22 Задача
Вот задача индийского математика 12в. Бхаскары
На
берегу реки рос тополь одинокий. Вдруг ветра порыв его ствол надломал. Бедный тополь упал. И угол прямой с теченьем реки его ствол составлял. Запомни теперь, что в том месте река в четыре лишь фута была широка. Верхушка склонилась у края реки. Осталось три фута всего от ствола, прошу тебя, скоро теперь мне скажи: у тополя как велика высота?
Решение:
По теореме Пифагора находим СD:
CD = 3 + 4 = 9 + 16 =25 => CD= 5.
Высота тополя равна: CB+CA. Т.к. CD=CB =>
AB=AC+CD= 3 + 5 = 8.
Ответ: высота тополя 8 футов.
2
2
2
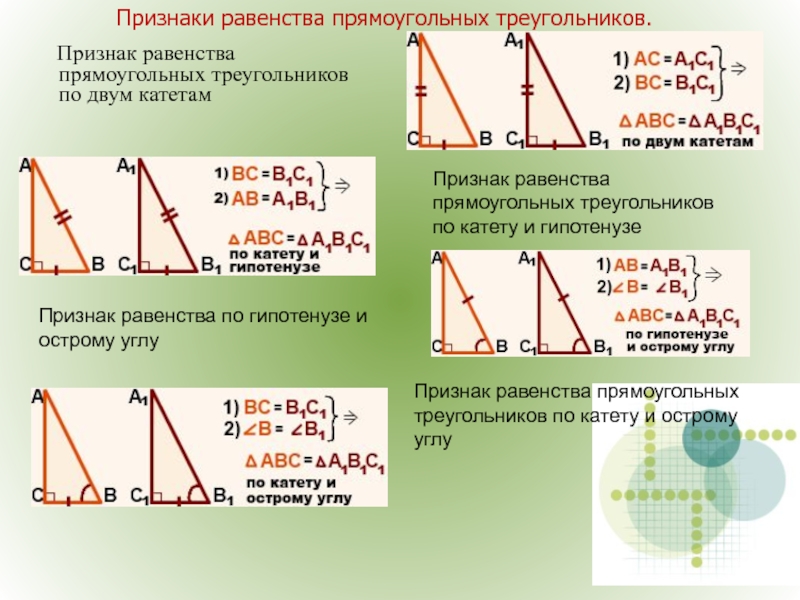
Слайд 23Признаки равенства прямоугольных треугольников.
Признак равенства прямоугольных треугольников по двум
катетам
Признак равенства прямоугольных треугольников по катету и гипотенузе
Признак равенства по гипотенузе и острому углу
Признак равенства прямоугольных треугольников по катету и острому углу
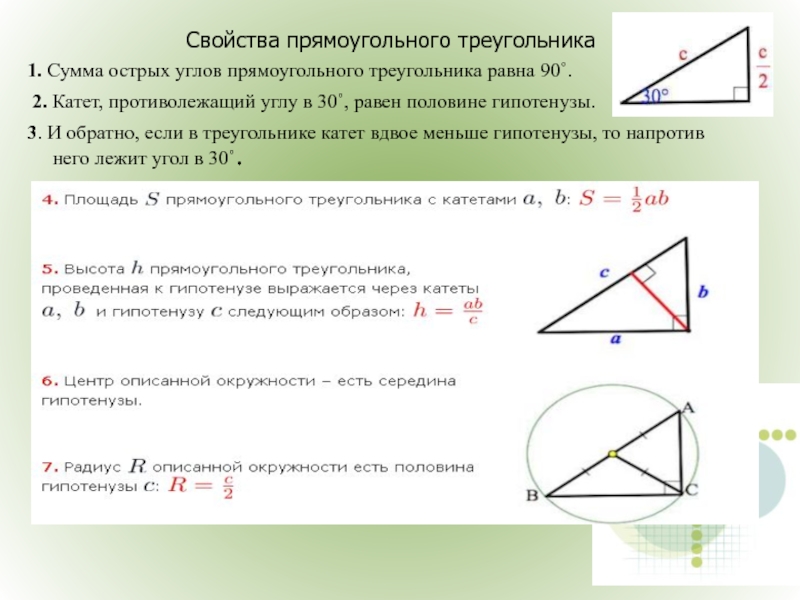
Слайд 24Свойства прямоугольного треугольника
1. Сумма острых углов прямоугольного треугольника равна 90˚.
2. Катет, противолежащий углу
в 30˚, равен половине гипотенузы.
3. И обратно, если в треугольнике катет вдвое меньше гипотенузы, то напротив него лежит угол в 30˚.
3. И обратно, если в треугольнике катет вдвое меньше гипотенузы, то напротив него лежит угол в 30˚.
