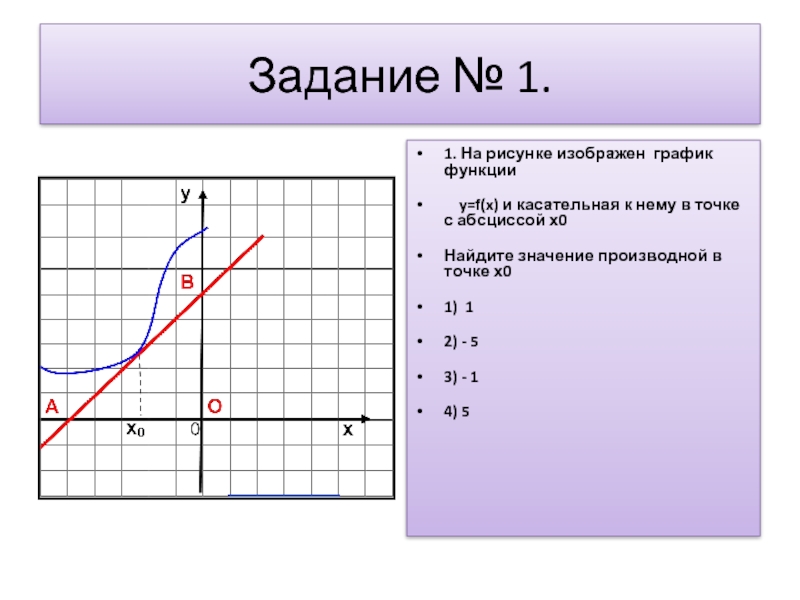
касательная к нему в точке с абсциссой х0
Найдите значение производной в точке х0
1) 1
2) - 5
3) - 1
4) 5
- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Тренажёр по алгебре по теме: Производная функции презентация
Содержание
- 2. Задание № 1. 1. На рисунке изображен
- 3. Задание № 2 2. На рисунке изображен
- 4. Задание № 3. 3. На рисунке изображен
- 5. Задание № 4. 4. На рисунке изображен
- 6. Задание № 5. Функция задана графиком. 5.
- 7. Задание № 6. 17. По графику функции
- 8. Задание № 7. 18. На рисунке
- 9. Задание № 8. 19. На рисунке
- 10. Задание № 9. В 20. Дан график
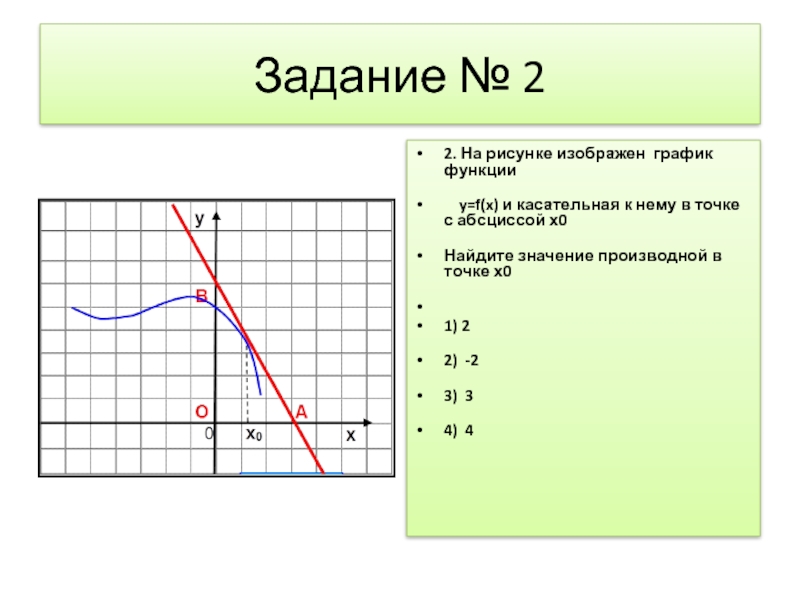
Слайд 3Задание № 2
2. На рисунке изображен график функции
y=f(x) и
касательная к нему в точке с абсциссой х0
Найдите значение производной в точке х0
1) 2
2) -2
3) 3
4) 4
Найдите значение производной в точке х0
1) 2
2) -2
3) 3
4) 4
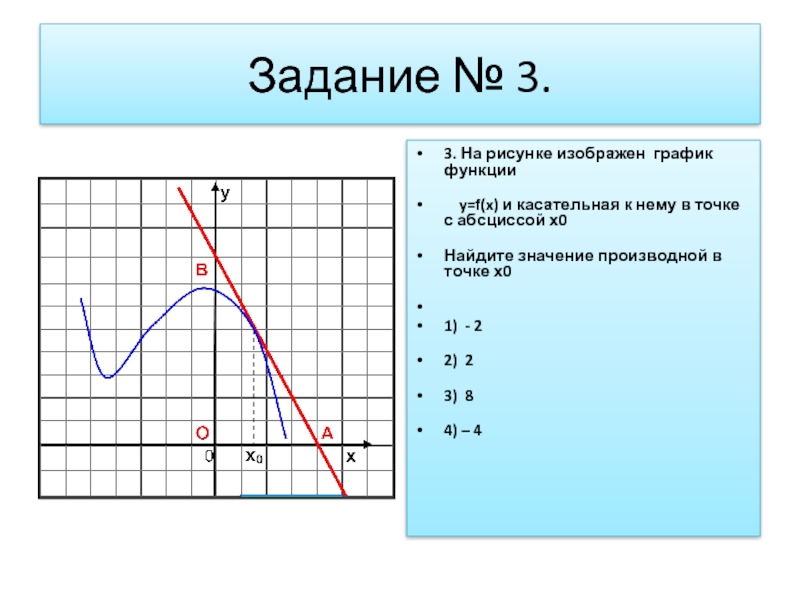
Слайд 4Задание № 3.
3. На рисунке изображен график функции
y=f(x) и
касательная к нему в точке с абсциссой х0
Найдите значение производной в точке х0
1) - 2
2) 2
3) 8
4) – 4
Найдите значение производной в точке х0
1) - 2
2) 2
3) 8
4) – 4
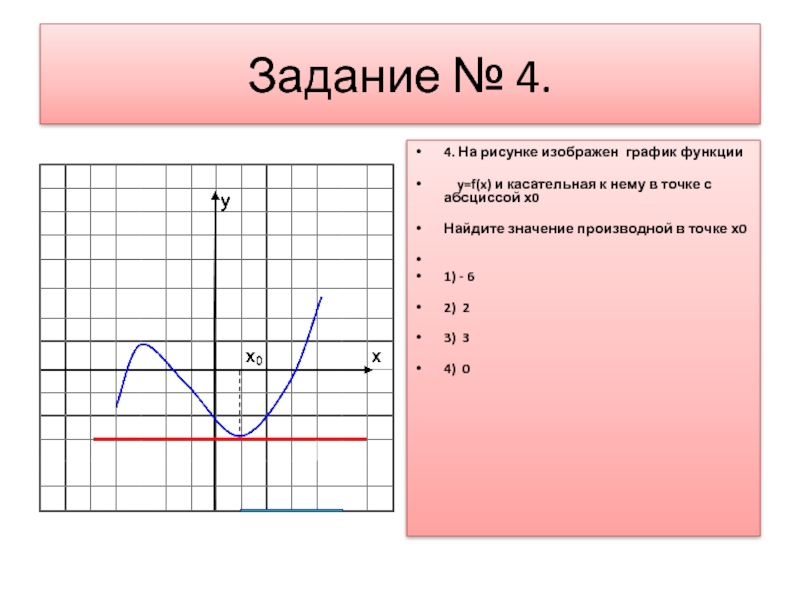
Слайд 5Задание № 4.
4. На рисунке изображен график функции
y=f(x) и
касательная к нему в точке с абсциссой х0
Найдите значение производной в точке х0
1) - 6
2) 2
3) 3
4) 0
Найдите значение производной в точке х0
1) - 6
2) 2
3) 3
4) 0
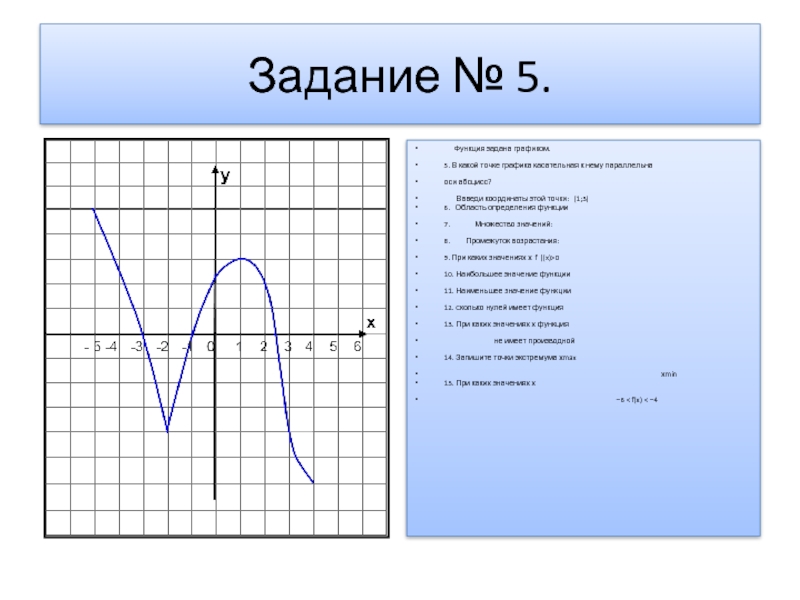
Слайд 6Задание № 5.
Функция задана графиком.
5. В какой точке графика касательная к
нему параллельна
оси абсцисс?
Ввведи координаты зтой точки: (1;3)
6. Область определения функции
7. Множество значений:
8. Промежуток возрастания:
9. При каких значениях х f |(x)>0
10. Наибольшее значение функции
11. Наименьшее значение функции
12. Cколько нулей имеет функция
13. При каких значениях х функция
не имеет производной
14. Запишите точки экстремума хmax
хmin
15. При каких значениях х
−6 < f(x) < −4
оси абсцисс?
Ввведи координаты зтой точки: (1;3)
6. Область определения функции
7. Множество значений:
8. Промежуток возрастания:
9. При каких значениях х f |(x)>0
10. Наибольшее значение функции
11. Наименьшее значение функции
12. Cколько нулей имеет функция
13. При каких значениях х функция
не имеет производной
14. Запишите точки экстремума хmax
хmin
15. При каких значениях х
−6 < f(x) < −4
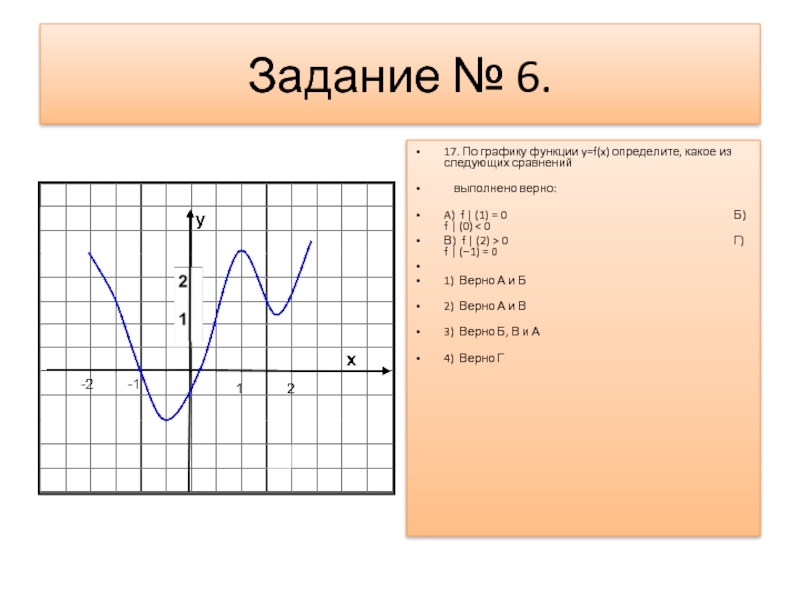
Слайд 7Задание № 6.
17. По графику функции y=f(x) определите, какое из следующих
сравнений
выполнено верно:
A) f | (1) = 0 Б) f | (0) < 0
В) f | (2) > 0 Г) f | (−1) = 0
1) Верно А и Б
2) Верно А и В
3) Верно Б, В и А
4) Верно Г
выполнено верно:
A) f | (1) = 0 Б) f | (0) < 0
В) f | (2) > 0 Г) f | (−1) = 0
1) Верно А и Б
2) Верно А и В
3) Верно Б, В и А
4) Верно Г
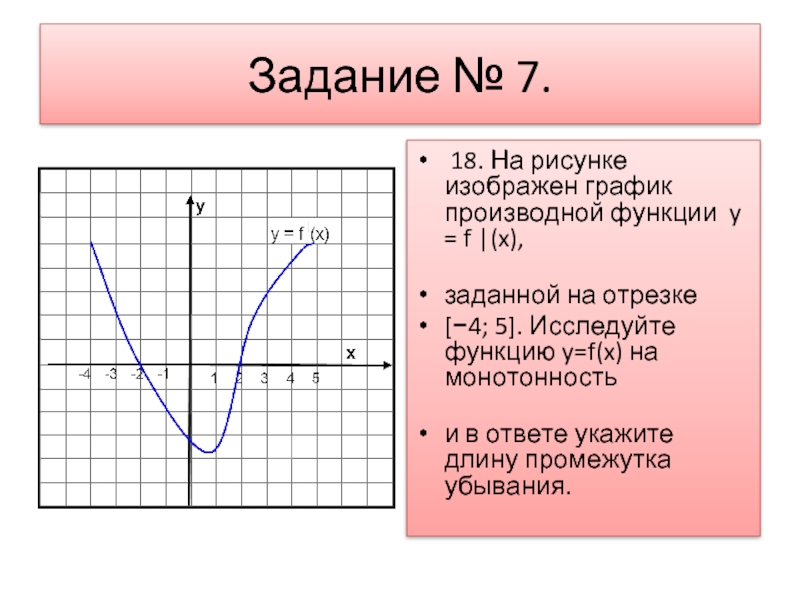
Слайд 8Задание № 7.
18. На рисунке изображен график производной функции y
= f |(x),
заданной на отрезке
[−4; 5]. Исследуйте функцию y=f(x) на монотонность
и в ответе укажите длину промежутка убывания.
заданной на отрезке
[−4; 5]. Исследуйте функцию y=f(x) на монотонность
и в ответе укажите длину промежутка убывания.
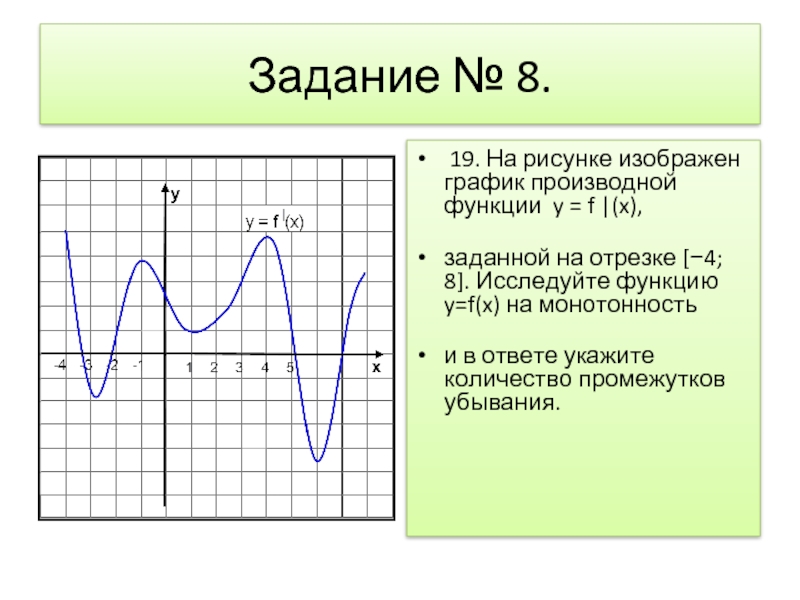
Слайд 9Задание № 8.
19. На рисунке изображен график производной функции y
= f |(x),
заданной на отрезке [−4; 8]. Исследуйте функцию y=f(x) на монотонность
и в ответе укажите количество промежутков убывания.
заданной на отрезке [−4; 8]. Исследуйте функцию y=f(x) на монотонность
и в ответе укажите количество промежутков убывания.
Слайд 10Задание № 9.
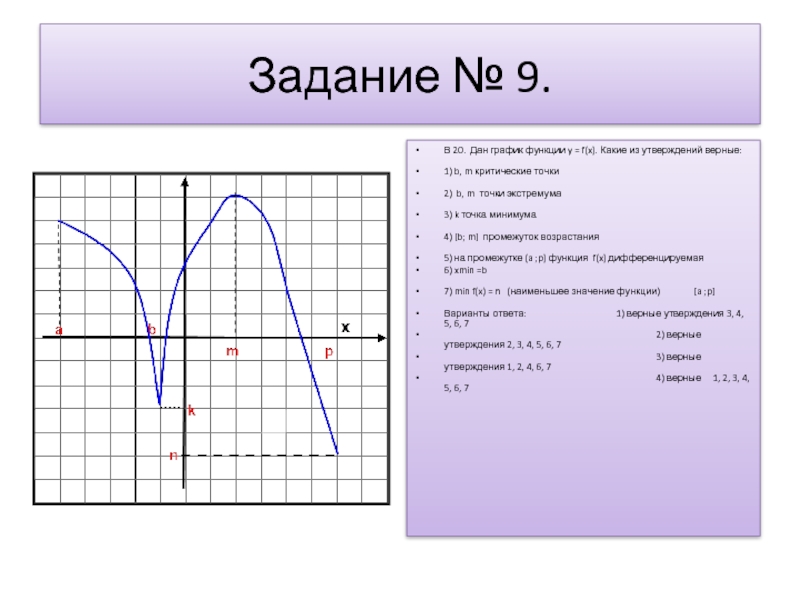
В 20. Дан график функции y = f(x). Какие
из утверждений верные:
1) b, m критические точки
2) b, m точки экстремума
3) k точка минимума
4) [b; m] промежуток возрастания
5) на промежутке (a ;p) функция f(x) дифференцируемая
6) xmin =b
7) min f(x) = n (наименьшее значение функции) [a ;p]
Варианты ответа: 1) верные утверждения 3, 4, 5, 6, 7
2) верные утверждения 2, 3, 4, 5, 6, 7
3) верные утверждения 1, 2, 4, 6, 7
4) верные 1, 2, 3, 4, 5, 6, 7
1) b, m критические точки
2) b, m точки экстремума
3) k точка минимума
4) [b; m] промежуток возрастания
5) на промежутке (a ;p) функция f(x) дифференцируемая
6) xmin =b
7) min f(x) = n (наименьшее значение функции) [a ;p]
Варианты ответа: 1) верные утверждения 3, 4, 5, 6, 7
2) верные утверждения 2, 3, 4, 5, 6, 7
3) верные утверждения 1, 2, 4, 6, 7
4) верные 1, 2, 3, 4, 5, 6, 7