- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Тіла обертання презентация
Содержание
- 1. Тіла обертання
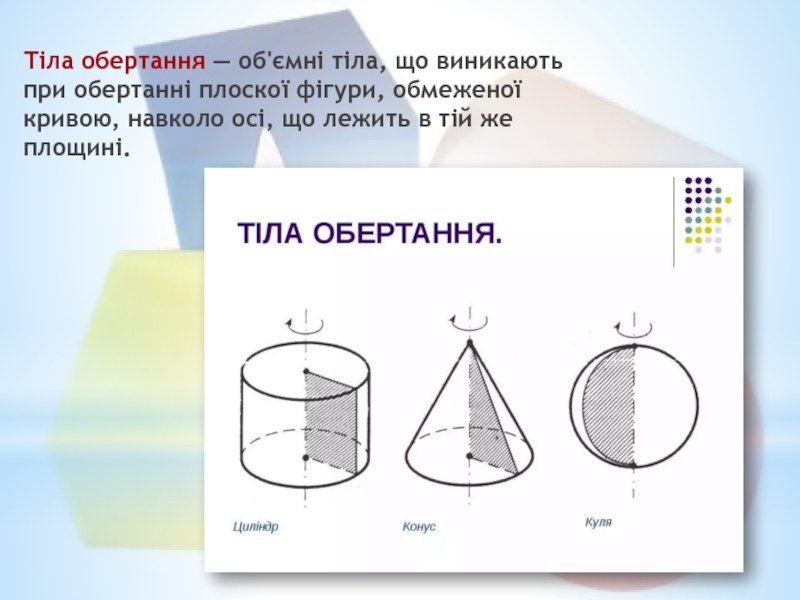
- 2. Тіла обертання — об'ємні тіла, що виникають
- 3. Приклади тіл обертання Куля — тривимірна фігура, утворена півколом, що обертається навколо діаметра розрізу.
- 4. Циліндр — тривимірна фігура, утворена прямокутником, що
- 5. Конус — тривимірна фігура, утворена прямокутним трикутником,
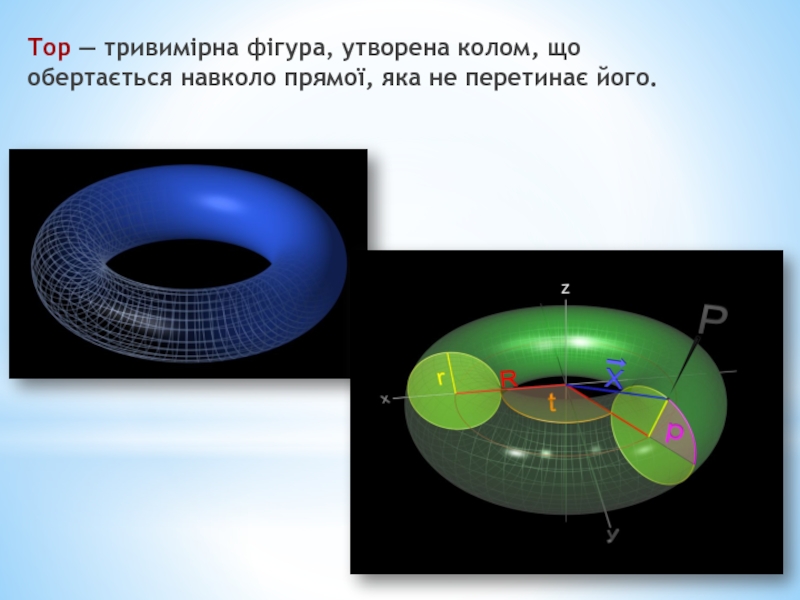
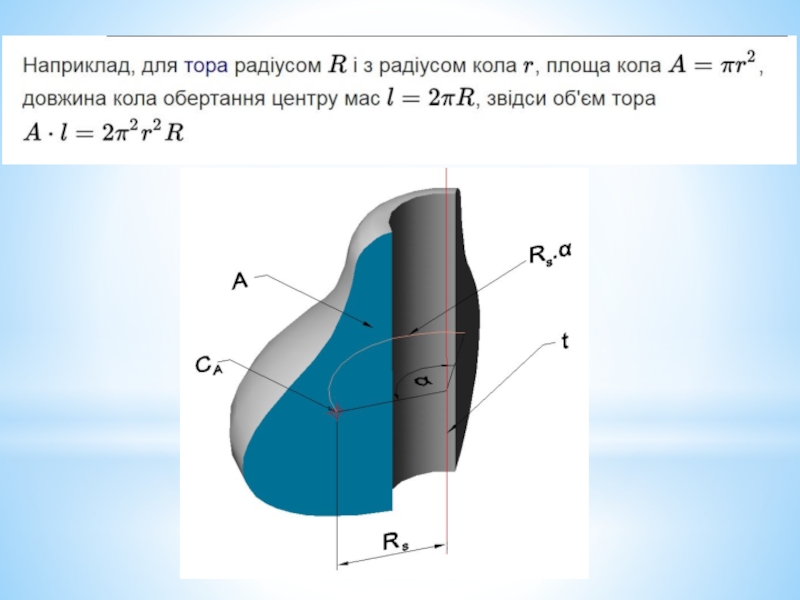
- 6. Тор — тривимірна фігура, утворена колом, що обертається навколо прямої, яка не перетинає його.
- 7. При обертанні контурів фігур виникає поверхня обертання
- 8. Об'єм і площа поверхні тіл обертання Об'єм
- 9. Перша теорема Гульдіна-Паппа стверджує: Площа поверхні,
- 11. Друга теорема Гульдіна-Паппа стверджує: Об'єм тіла,
- 13. Нехай графік функції y = f (x)
- 14. Обчислення об'єму тіла обертання навколо осі Оy
Тіла обертання — об'ємні тіла, що виникають при обертанні плоскої фігури, обмеженої кривою, навколо осі, що лежить в тій же площині.
Слайд 2Тіла обертання — об'ємні тіла, що виникають при обертанні плоскої фігури,
обмеженої кривою, навколо осі, що лежить в тій же площині.
Слайд 3Приклади тіл обертання
Куля — тривимірна фігура, утворена півколом, що обертається навколо
діаметра розрізу.
Слайд 4Циліндр — тривимірна фігура, утворена прямокутником, що обертається навколо однієї із
сторін
За площу бічної поверхні циліндра приймається площа її розгортки:
Sбіч = 2πrh
За площу бічної поверхні циліндра приймається площа її розгортки:
Sбіч = 2πrh
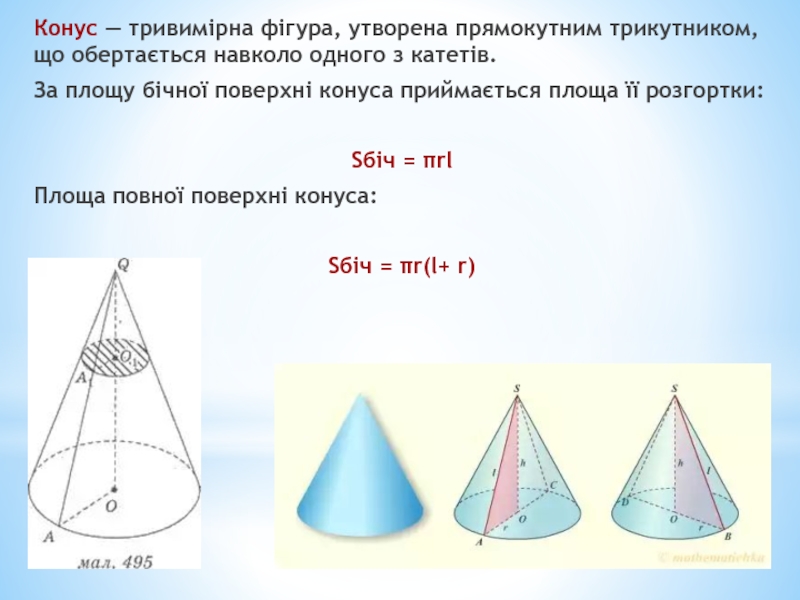
Слайд 5Конус — тривимірна фігура, утворена прямокутним трикутником, що обертається навколо одного
з катетів.
За площу бічної поверхні конуса приймається площа її розгортки:
Sбіч = πrl
Площа повної поверхні конуса:
Sбіч = πr(l+ r)
За площу бічної поверхні конуса приймається площа її розгортки:
Sбіч = πrl
Площа повної поверхні конуса:
Sбіч = πr(l+ r)
Слайд 6Тор — тривимірна фігура, утворена колом, що обертається навколо прямої, яка
не перетинає його.
Слайд 7При обертанні контурів фігур виникає поверхня обертання (наприклад, сфера, утворена колом),
в той час як при обертанні заповнених контурів виникають тіла (як куля, утворена кругом).
Слайд 8Об'єм і площа поверхні тіл обертання
Об'єм і площа поверхні тіл обертання
можна дізнатися за допомогою теорем Гульдіна-Паппа
Слайд 9Перша теорема Гульдіна-Паппа
стверджує:
Площа поверхні, утвореної при обертанні лінії, що лежить
в площині цілком по одну сторону від осі обертання, дорівнює добутку довжини лінії s на довжину кола l = 2πrs, яке пробігає центр мас (т.С) цієї лінії.
Слайд 11Друга теорема Гульдіна-Паппа
стверджує:
Об'єм тіла, утвореного при обертанні фігури, що лежить
в площині цілком по одну сторону від осі обертання, дорівнює добутку площі А фігури на довжину кола l = 2πRs, яке пробігає центр мас (т.CA) цієї фігури.
Слайд 13Нехай графік функції y = f (x) обертається навколо осі Ox,
утворюючи так звану поверхню обертання. Визначимо об'єм тіла, обмеженого цією поверхнею і площинами x = a, x = b.
Об'єм тіла обертання, утвореного обертанням графіка y = f (x) навколо осі Ox, може бути обчислений за формулою:
1. Обчислити об'єм тіла, утвореного обертанням дуги кривої y = x2, x∈ [1,3] навколо осі Оx.
Рішення. Дані a = 1, b = 3, f (x) = x2, підставляємо в формулу, отримуємо:
Обчислення об'єму тіла обертання навколо осі Ох
Слайд 14Обчислення об'єму тіла обертання навколо осі Оy
Нехай графік функції x =
φ (y) обертається навколо осі Oy, утворюючи так звану поверхню обертання. Визначимо об'єм тіла, обмеженого цією поверхнею і площинами y = c, y = d.
Об'єм тіла обертання, утвореного обертанням графіка x = φ (y) навколо осі Oy, може бути обчислений за формулою:
Приклад 2. Обчислити об'єм тіла, утвореного обертанням дуги кривої x = 3y-y2, x∈ [1,2] навколо осі Оx.
Рішення. Дані c = 1, d = 2, φ (y) = 3y-y2, підставляємо в формулу, отримуємо:
У калькулятор вставляємо функцію x = 3y-y2, x міняємо на y, кордони від 1 до 2, перевіряємо правильність обчислення об'єму, а також отримуємо малюнок тіла обертання.
