- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Теория кривых. Эволюта и Эвольвента презентация
Содержание
- 1. Теория кривых. Эволюта и Эвольвента
- 2. Эволюта Определение: нормалью плоской кривой называется прямая,
- 3. Эволюта уравнением. направлен вдоль нормали плоской
- 4. Уравнение эволюты Определение: огибающая семейства нормалей плоской
- 5. Уравнение эволюты (46) (46) – параметрические уравнения эволюты.
- 6. Эвольвента Определение: ортогональной траекторией данного семейства
- 7. Эвольвента Определение: ортогональная траектория семейства касательных
- 8. Уравнение эвольвенты Пусть - уравнение
- 9. Натуральные уравнения пространственной кривой
Эволюта Определение: нормалью плоской кривой называется прямая, перпендикулярная касательной, проходящая через точку касания и лежащая в плоскости этой кривой. Нормаль плоской кривой совпадает с главной
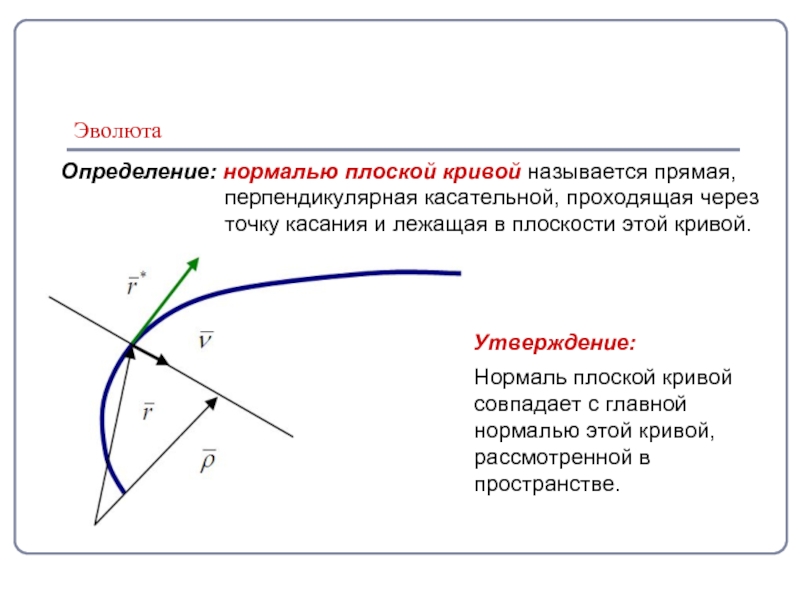
Слайд 2Эволюта
Определение: нормалью плоской кривой называется прямая,
перпендикулярная касательной, проходящая через
точку
касания и лежащая в плоскости этой кривой.
Нормаль плоской кривой
совпадает с главной
нормалью этой кривой,
рассмотренной в
пространстве.
Утверждение:
Слайд 3Эволюта
уравнением.
направлен вдоль нормали плоской кривой с неявным
(43)
(43) – уравнение нормали плоской
кривой, где
(x; y) – точка,
лежащая на кривой.
нормали
(44)
(44) – уравнение нормали плоской кривой, заданной
параметрическими уравнениями.
Слайд 4Уравнение эволюты
Определение: огибающая семейства нормалей плоской кривой
называется эволютой.
Уравнения (44) и (44’) можно записать в виде:
Продифференцируем это уравнение по t:
(45)
Распишем уравнения (44’) и (45) по координатам и найдем их
решение:
Слайд 6Эвольвента
Определение: ортогональной траекторией данного семейства
плоских кривых называется кривая, которая
пересекает каждую кривую данного семейства под
прямым углом.
пересекает каждую кривую данного семейства под
прямым углом.
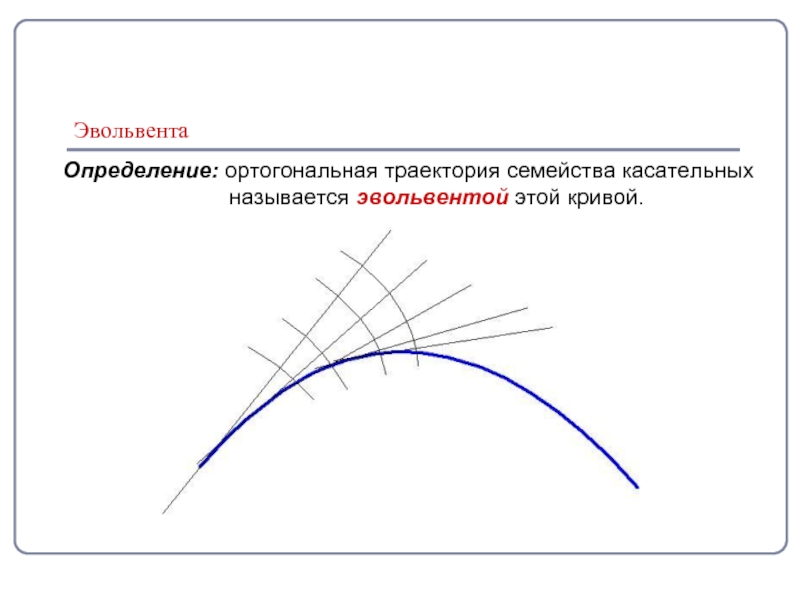
Слайд 7Эвольвента
Определение: ортогональная траектория семейства касательных
называется эвольвентой этой кривой.
Слайд 8Уравнение эвольвенты
Пусть
- уравнение кривой,
- касательный вектор,
- радиус-вектор точек
на эвольвенте.
(47)
(47) – уравнение эвольвенты.
Слайд 9Натуральные уравнения пространственной кривой
Утверждение:
2 эвольвенты одной кривой являются эквидистантными линиями.
Натуральные уравнения
пространственной кривой.
(48)
(48) – натуральные уравнения пространственной кривой.
