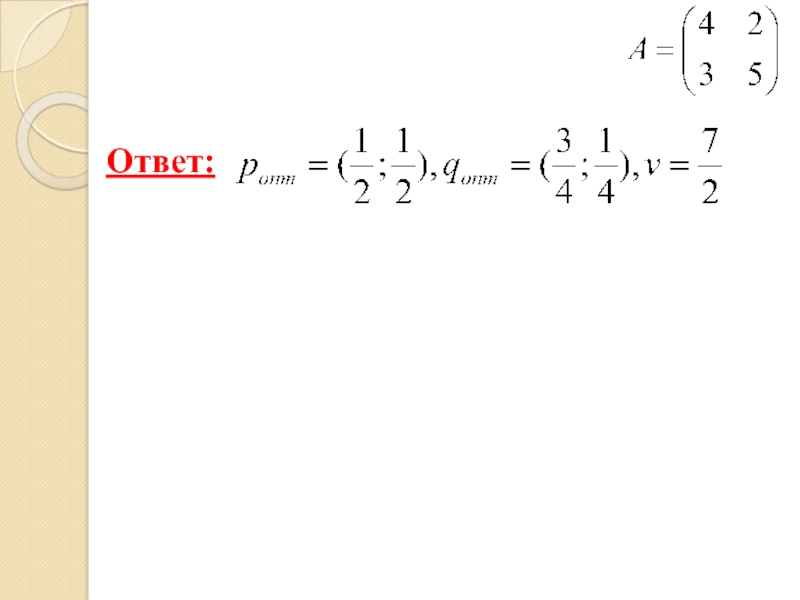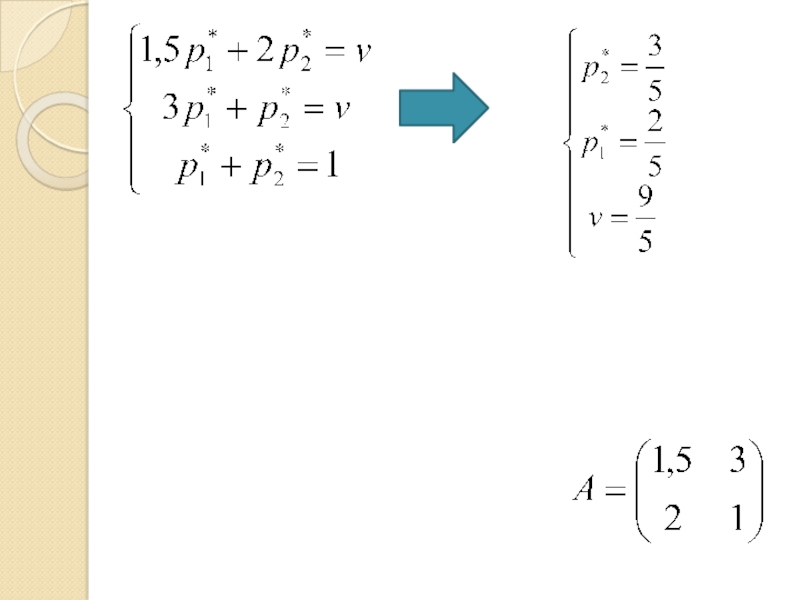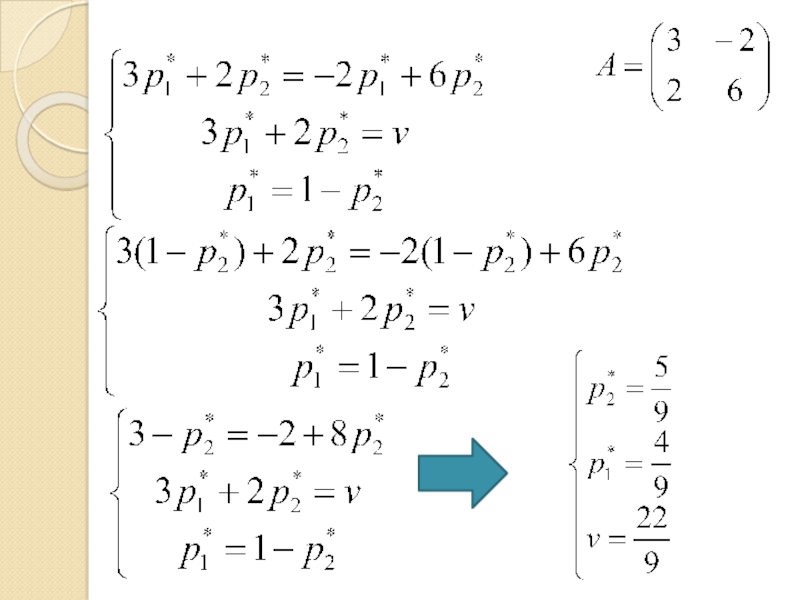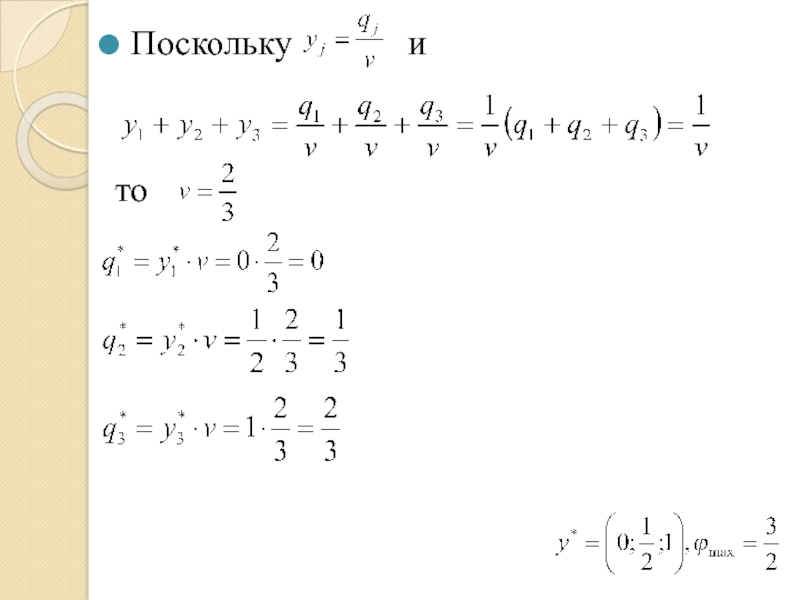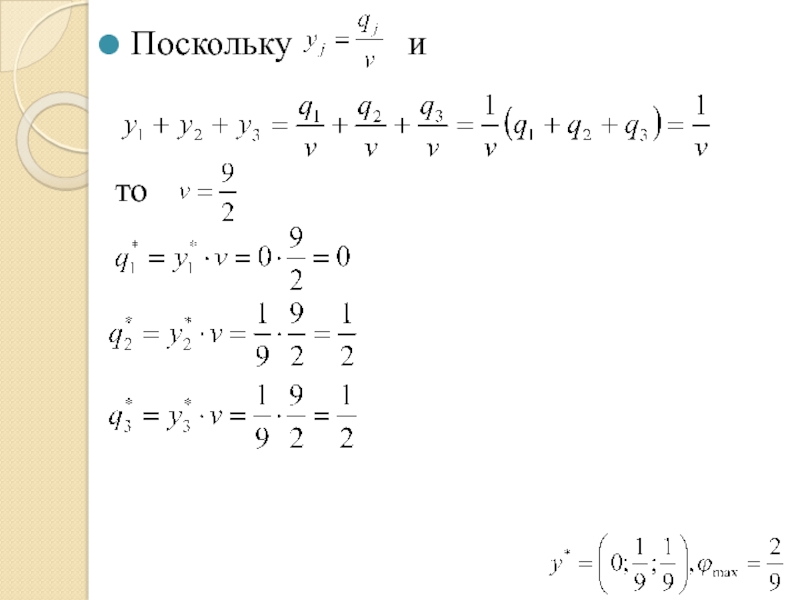- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Теория игр. Платежная матрица. (Семинар 2) презентация
Содержание
- 1. Теория игр. Платежная матрица. (Семинар 2)
- 2. Платежная матрица Пусть игрок A располагает m
- 3. Нижняя цена игры Пусть αi –
- 4. Верхняя цена игры Число β –
- 5. Задача 1 Найдите седловую точку
- 6. Решение: Найдем минимальные значения каждой строки матрицы
- 7. Найдем верхнюю цену игры. Для этого определим
- 8. Получаем: α = β = 0,3 v = 0,3 Седловая точка - (A2B3)
- 9. Задача 2 Найдите седловую точку
- 10. Решение: Нижняя цена игры: α1 =
- 11. Верхняя цена игры: β1 =
- 12. Получаем: α = β = 6 v = 6 Седловая точка - (A2B4)
- 13. Решение игры в смешанных стратегиях Если α
- 14. Смешанная стратегия SА игрока А –
- 15. Задача 3 Найдите решение игры
- 16. Решение: Найдем нижнюю и верхнюю цену
- 17. Средний выигрыш игрока А также равен
- 18. Решаем систему:
- 19. Составим аналогичную систему для игрока В:
- 20. Ответ:
- 21. Задача 4 Найдите решение игры
- 22. Решение: Найдем нижнюю и верхнюю цену
- 23. Решение: Найдем нижнюю и верхнюю цену
- 25. Составим аналогичную систему для игрока В:
- 26. Ответ:
- 27. Задача 3 Найдите решение игры
- 28. Решение: Найдем нижнюю и верхнюю цену
- 29. Решение: Найдем нижнюю и верхнюю цену
- 30. В1 В2 В1 y Пусть игрок В
- 31. В1 В2 В1 y Точки, лежащие на
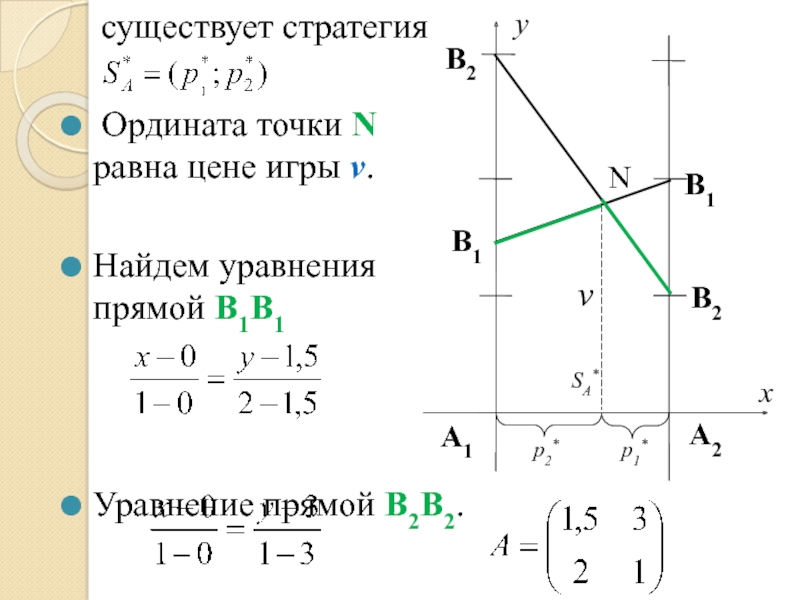
- 32. В1 В2 В1 y существует стратегия
- 33. Получаем систему уравнений:
- 34. Определим аналогично геометрическим способом оптимальную стратегию игрока
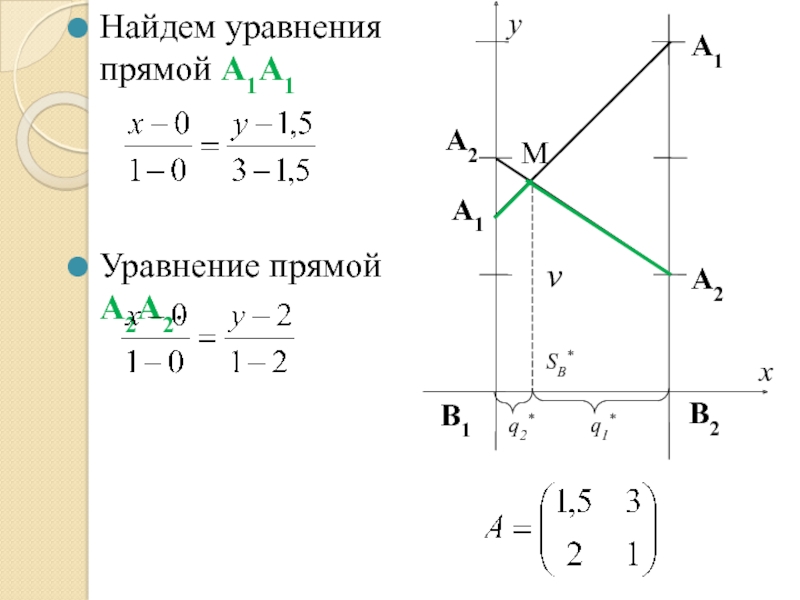
- 35. А1 А2 А1 y Найдем уравнения прямой
- 36. Получаем систему уравнений: Ответ:
- 37. Задача 4 Найдите
- 38. Решение: Найдем нижнюю и верхнюю цену
- 39. Решение: Найдем нижнюю и верхнюю цену
- 40. В1 В2 В1 y Пусть игрок В
- 41. В1 В2 В1 y Точки, лежащие на
- 42. В1 В2 В1 y существует стратегия
- 43. Получаем систему уравнений:
- 44. Определим аналогично геометрическим способом оптимальную стратегию игрока
- 45. А1 А2 А1 y Найдем уравнения прямой
- 46. Получаем систему уравнений: Ответ:
- 47. Если в платежной матрице A все элементы
- 48. Игроку А не выгодно применять стратегии, которым
- 49. Задача 5 Найти
- 50. Найдем нижнюю и верхнюю цену игры:
- 51. Найдем нижнюю и верхнюю цену игры:
- 52. Удаляем не выгодные для игроков А и
- 53. Удаляем не выгодные для игроков А и
- 55. Для игрока В:
- 56. Для игрока В:
- 57. Ответ:
- 58. Задача 6 Найти решение игры
- 59. Найдем нижнюю и верхнюю цену игры:
- 60. Найдем нижнюю и верхнюю цену игры:
- 61. Для игрока В при сравнении: В1 и
- 62. Решим полученную задачу аналитическим способом. Для игрока А:
- 63. Для игрока В:
- 64. Для игрока В:
- 65. Ответ:
- 66. Приведение матричной игры к задаче линейного программирования
- 67. Пусть v > 0, тогда для оптимальной
- 68. Цель игрока A – максимизировать свой гарантированный
- 69. Получаем задачу линейного программирования:
- 70. Для определения оптимальной стратегии SВ*игрока B следует
- 71. Задача 7 Найти решение игры с помощью линейного программирования.
- 72. Найдем нижнюю и верхнюю цену игры:
- 73. Найдем нижнюю и верхнюю цену игры:
- 74. Приведем полученную систему к каноническому виду:
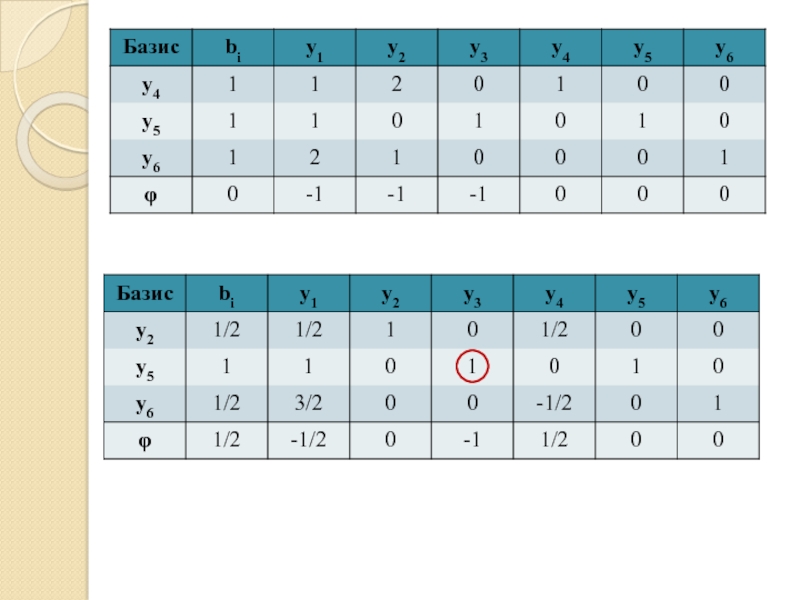
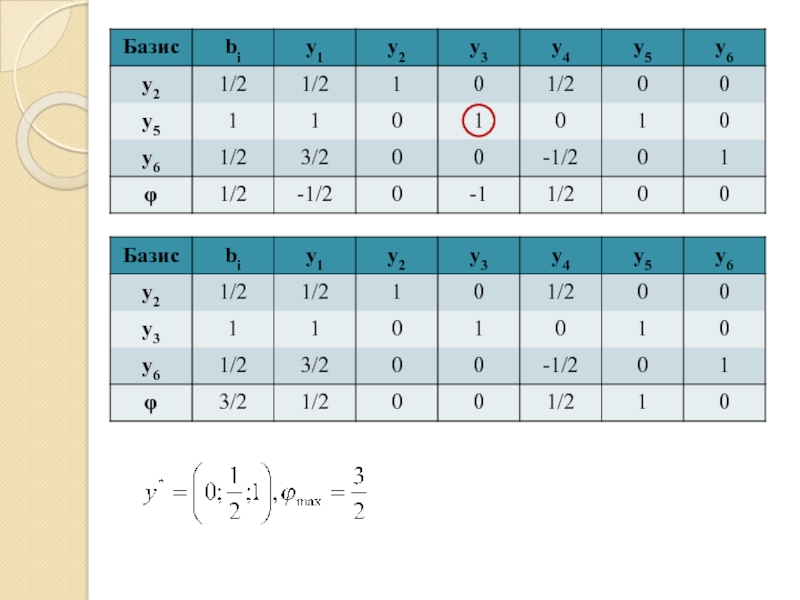
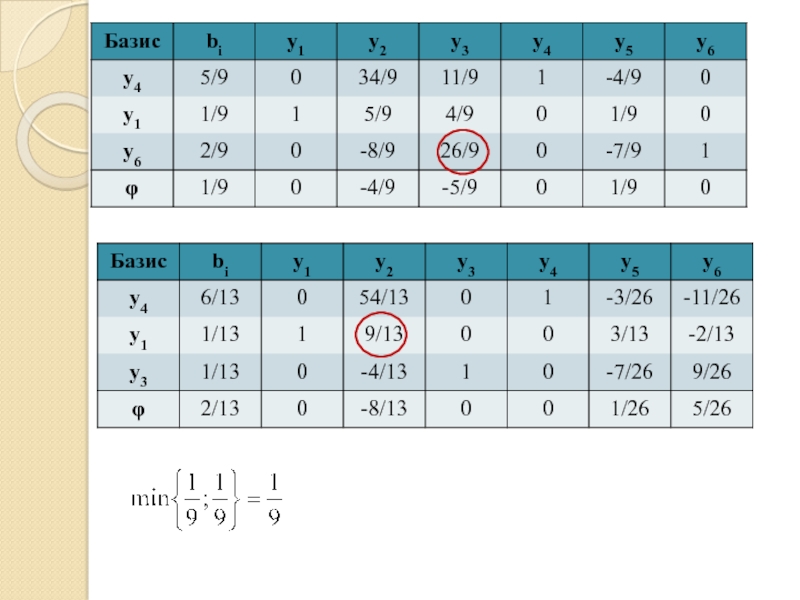
- 75. Решим полученную задачу линейного программирования симплекс-методом:
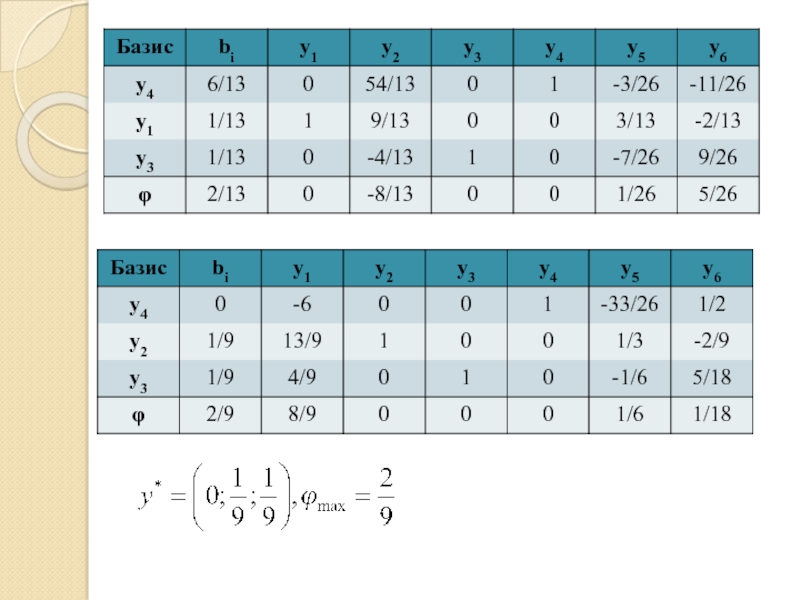
- 78. Поскольку
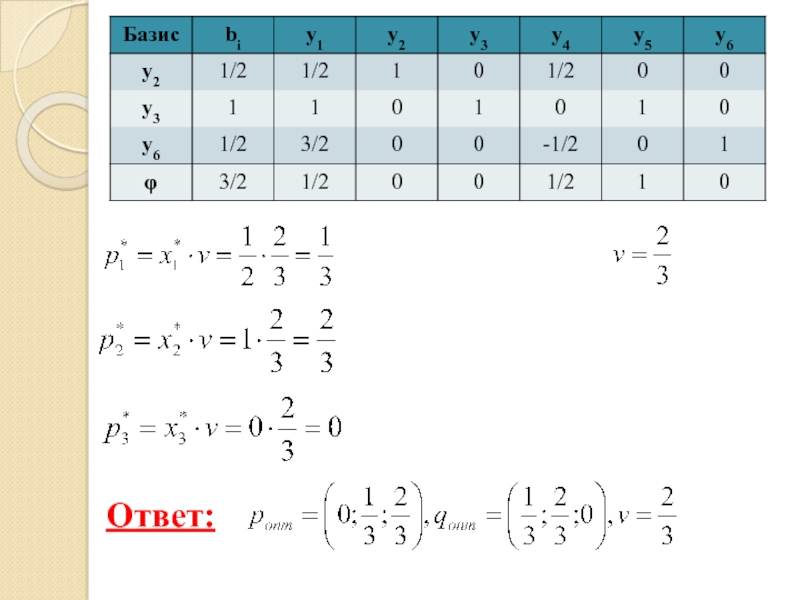
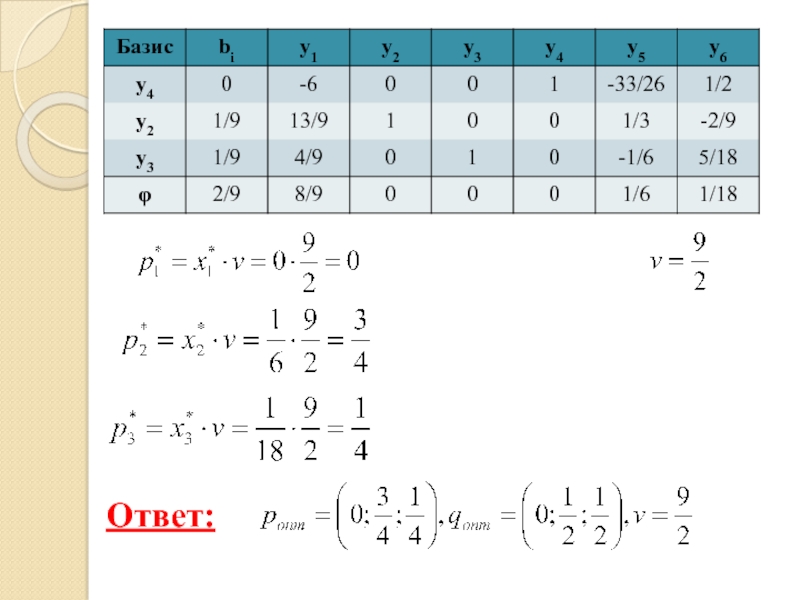
- 79. Ответ:
- 80. Задача 8 Найти решение игры с помощью линейного программирования.
- 81. Найдем нижнюю и верхнюю цену игры:
- 82. Найдем нижнюю и верхнюю цену игры:
- 83. Приведем полученную систему к каноническому виду:
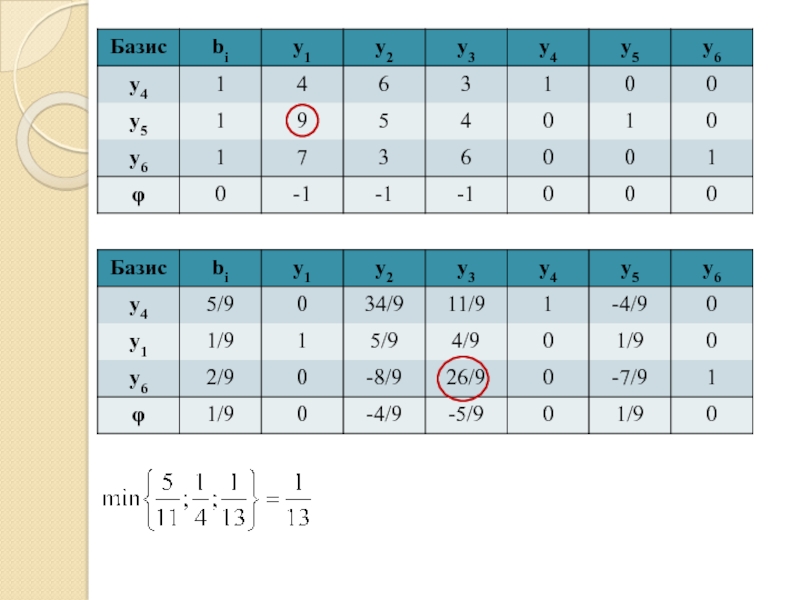
- 84. Решим симплекс-методом:
- 88. Поскольку
- 89. Ответ:
- 90. Игра с природой - матричная игра,
- 91. Игра с природой Пусть A1 , A2,
- 92. Есть другой способ задания матрицы игры с
- 93. Для определения оптимальной стратегии игрока A в
- 94. Критерий Cэвиджа – использует матрицу рисков
- 95. Критерий Гурвица – при любом выборе
- 96. Критерий Лапласа – все состояния природы
- 97. Задача 9 Найти оптимальную стратегию
- 98. 1. Найдем критерий Вальда.
- 99. 2. Найдем критерий Сэвиджа. Для матрицы
- 100. Найдем наибольший элемент каждой строки матрицы R,
- 101. 3. Найдем критерий Гурвица. (α = 0,3)
- 102. 4. Найдем критерий Лапласа. n = 3
- 103. Ответ: По критерию Вальда оптимальные
- 104. Задача 10 Найти оптимальную стратегию
- 105. 1. Найдем критерий Вальда.
- 106. 2. Найдем критерий Сэвиджа. Для матрицы
- 107. Найдем наибольший элемент каждой строки матрицы R,
- 108. 3. Найдем критерий Гурвица. (α = 0,3)
- 109. 4. Найдем критерий Лапласа. n = 3
- 110. Ответ: По критерию Вальда оптимальная
- 111. Спасибо за внимание!
Слайд 2Платежная матрица
Пусть игрок A располагает m стратегиями A1 , A2, …,
Выигрыш игрока A при выборе стратегий Ai и Bj обозначим aij.
Платежная матрица (матрица игры):
Слайд 3
Нижняя цена игры
Пусть αi – наименьший выигрыш игрока A при выборе
Тогда гарантированный выигрыш игрока A при любой стратегии игрока B равен:
α – нижняя цена игры.
Слайд 4
Верхняя цена игры
Число β – верхняя цена игры:
β - гарантированный проигрыш
Если α = β = v, то v – чистая цена (или цена игры). Тогда пара оптимальных стратегий Ai и Bj, для которой aij = v называется седловой точкой платежной матрицы.
Слайд 5Задача 1
Найдите седловую точку в игре с матрицей выигрышей
Слайд 6Решение:
Найдем минимальные значения каждой строки матрицы А и выберем из них
α1 = min (0,1; 0,4; 0,2) = 0,1
α2 = min (0,5; 0,4; 0,3) = 0,3
α3 = min (0,3; 0,2; 0,1) = 0,1
α = max (0,1; 0,3; 0,1) = 0,3
Слайд 7Найдем верхнюю цену игры. Для этого определим максимальное значение в каждом
β1 = max (0,1; 0,5; 0,3) = 0,5
β2 = max (0,4; 0,4; 0,2) = 0,4
β3 = max (0,2; 0,3; 0,1) = 0,3
β = min (0,5; 0,4; 0,3) = 0,3
Слайд 9Задача 2
Найдите седловую точку в игре с матрицей выигрышей
Слайд 10Решение:
Нижняя цена игры:
α1 = min (2; 10; 25; 0) =
α2 = min (13; 14; 19; 6) = 6
α3 = min (-5; 3; -2; -4) = - 5
α4 = min (18; 5; -3; -5) = - 5
α = max (0; 6 ; -5; -5) = 6
Слайд 11Верхняя цена игры:
β1 = max (2; 13; -5; 18)
β2 = max (10; 14; 3; 5) = 14
β3 = max (25; 19; -2; -3) = 25
β4 = max (0; 6; -4; -5) = 6
β = min (18; 14 ; 25; 6) = 6
Слайд 13Решение игры в смешанных стратегиях
Если α < β, то применение чистых
Оптимальное решение можно получить случайным образом путем чередования чистых стратегий – в смешанных стратегиях.
Слайд 14
Смешанная стратегия SА игрока А – применение чистых стратегий A1 ,
Для игрока B аналогично:
Слайд 16
Решение:
Найдем нижнюю и верхнюю цену игры:
α = 3, β =
Средний выигрыш игрока А равен цене игры v, если он использует оптимальную смешанную стратегию
игрок B использует чистую стратегию B1 (т.е. первый столбец платежной матрицы)
Слайд 17
Средний выигрыш игрока А также равен цене игры v, если игрок
Получаем систему:
Слайд 23
Решение:
Найдем нижнюю и верхнюю цену игры:
α = 1,5, β =
Система уравнений для игрока А:
Слайд 27Задача 3
Найдите решение игры в смешанных стратегиях графическим способом.
Слайд 29
Решение:
Найдем нижнюю и верхнюю цену игры:
α = 3, β =
На оси Оx отложим единичный отрезок A1A2.
Прямая x = 0 соответствует стратегии A1 игрока A, а прямая x = 1 соответствует стратегии A2.
Слайд 30В1
В2
В1
y
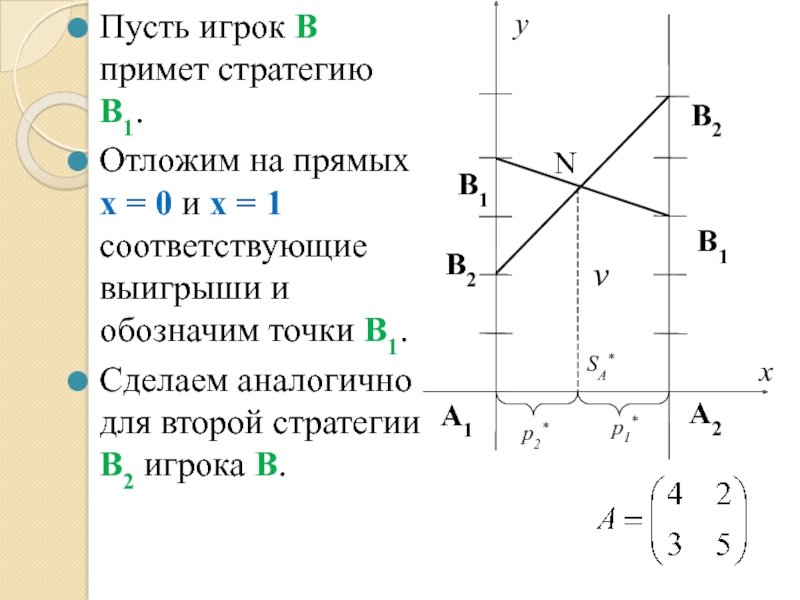
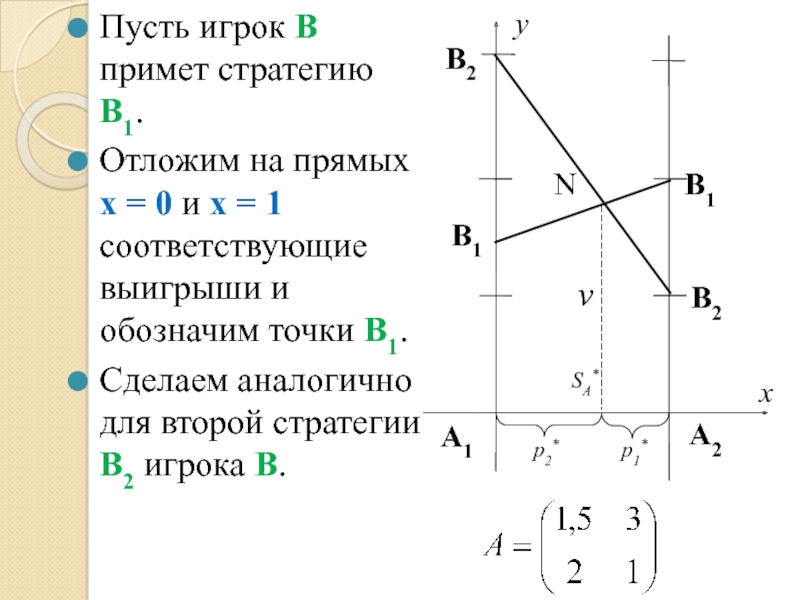
Пусть игрок В примет стратегию В1.
Отложим на прямых x = 0
Сделаем аналогично для второй стратегии В2 игрока В.
Слайд 31В1
В2
В1
y
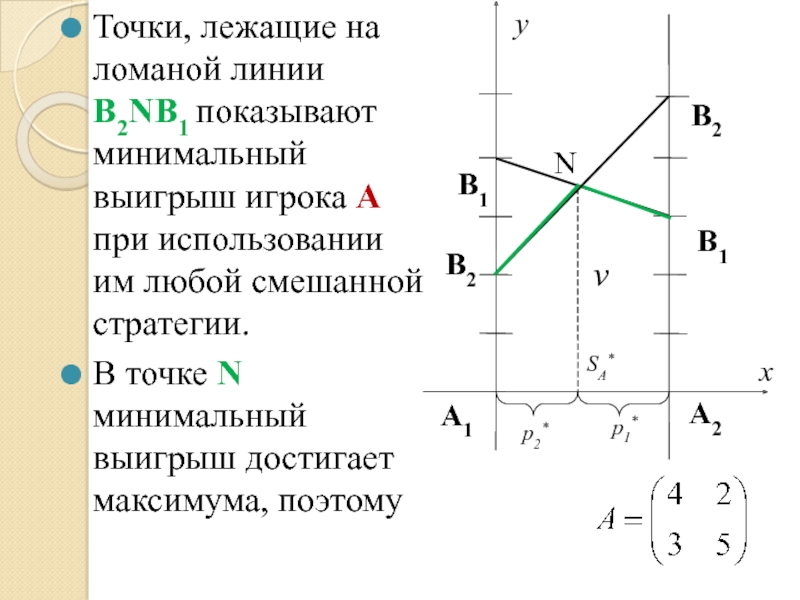
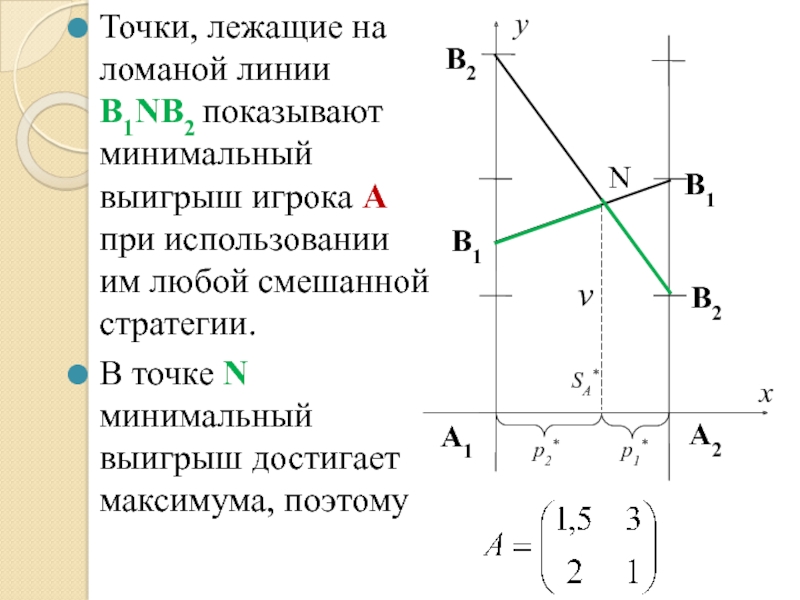
Точки, лежащие на ломаной линии В2NВ1 показывают минимальный выигрыш игрока A
В точке N минимальный выигрыш достигает максимума, поэтому
Слайд 32В1
В2
В1
y
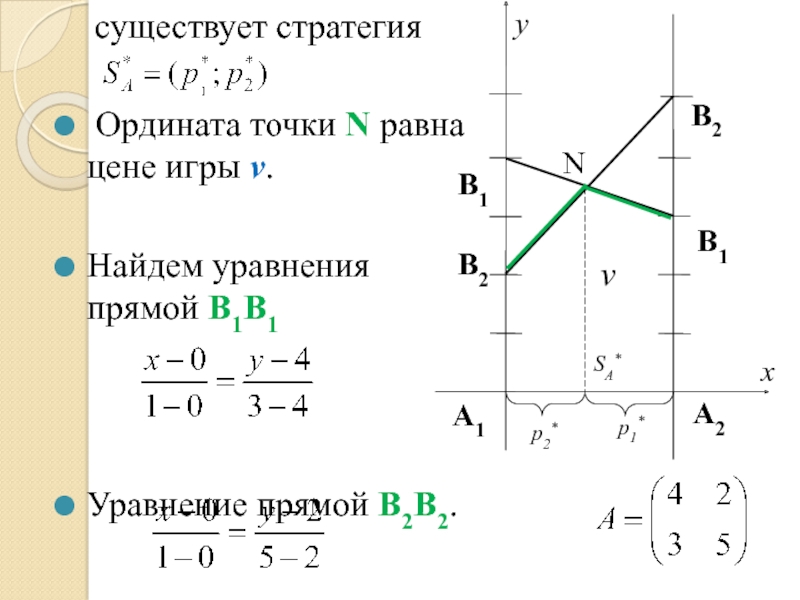
существует стратегия
Ордината точки N равна цене игры v.
Найдем уравнения
Уравнение прямой В2В2.
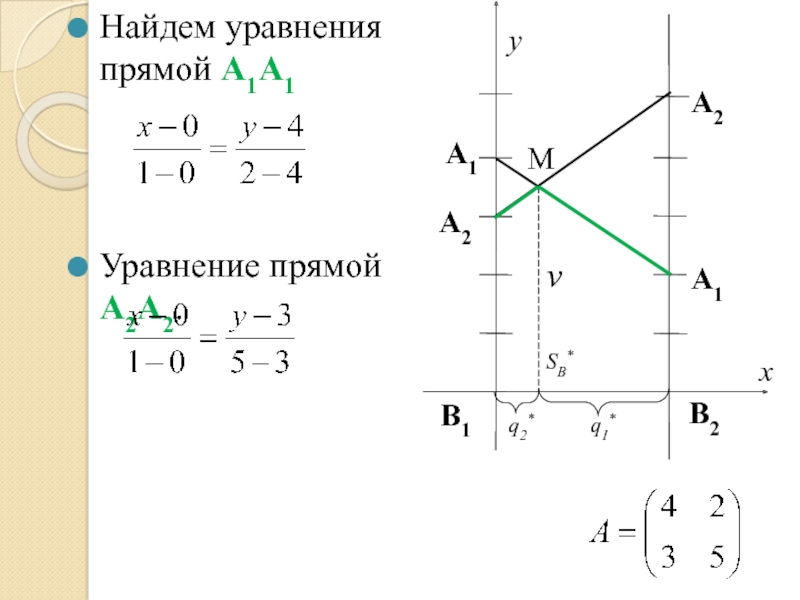
Слайд 34Определим аналогично геометрическим способом оптимальную стратегию игрока В.
Поменяем местами игроков А
Слайд 37Задача 4
Найдите решение игры в смешанных стратегиях графическим способом.
Слайд 39
Решение:
Найдем нижнюю и верхнюю цену игры:
α = 1,5, β
На оси Оx отложим единичный отрезок A1A2.
Прямая x = 0 соответствует стратегии A1 игрока A, а прямая x = 1 соответствует стратегии A2.
Слайд 40В1
В2
В1
y
Пусть игрок В примет стратегию В1.
Отложим на прямых x = 0
Сделаем аналогично для второй стратегии В2 игрока В.
Слайд 41В1
В2
В1
y
Точки, лежащие на ломаной линии В1NВ2 показывают минимальный выигрыш игрока A
В точке N минимальный выигрыш достигает максимума, поэтому
Слайд 42В1
В2
В1
y
существует стратегия
Ордината точки N равна цене игры v.
Найдем уравнения
Уравнение прямой В2В2.
Слайд 44Определим аналогично геометрическим способом оптимальную стратегию игрока В.
Поменяем местами игроков А
Слайд 47Если в платежной матрице A все элементы i-й строки не меньше
Доминирующие и доминируемые стратегии
Слайд 48Игроку А не выгодно применять стратегии, которым соответствуют доминируемые строки, а
При решении игры можно уменьшить размер платежной матрицы с помощью удаления из нее доминируемых строк и доминирующих столбцов.
Доминирующие и доминируемые стратегии
Слайд 49Задача 5
Найти решение игры в смешанных стратегиях, предварительно упростив
Слайд 51Найдем нижнюю и верхнюю цену игры:
α = 2, β =
Cтрока А3 доминируемая относительно строки А1, поэтому для игрока А она не выгодна.
Для игрока В не выгодны столбцы В1 и В2 .
Решение:
Слайд 52Удаляем не выгодные для игроков А и В стратегии и получаем
Решим полученную задачу аналитическим способом. Для игрока А:
Слайд 53Удаляем не выгодные для игроков А и В стратегии и получаем
Решим полученную задачу аналитическим способом. Для игрока А:
Слайд 58Задача 6
Найти решение игры в смешанных стратегиях, предварительно упростив
Слайд 60Найдем нижнюю и верхнюю цену игры:
α = 3, β =
Строка А2 доминируемая относительно строки А1 .
Строка А4 доминируемая строки А3.
Для игрока А они не выгодны.
Остается матрица:
Решение:
Слайд 61Для игрока В при сравнении:
В1 и В4 исключим столбец В1;
В2 и
В3 и В4 исключим столбец В3.
Остается матрица:
Слайд 66Приведение матричной игры к задаче линейного программирования
Пусть игрок A обладает Ai
i = 1, 2, …, m и игрок B имеет Bj стратегий
j = 1, 2, …, n.
Оптимальная стратегия SA* обеспечивает игроку A при любой стратегии игрока B средний выигрыш, не меньший, чем цена игры v, и при оптимальной стратегии игрока B выигрыш равный цене игры v.
Слайд 67Пусть v > 0, тогда для оптимальной стратегии SA* все средние
Пусть , тогда:
Слайд 69Получаем задачу линейного программирования:
Решением задачи будет оптимальная стратегия SA* игрока A.
Слайд 70Для определения оптимальной стратегии SВ*игрока B следует учесть, что игрок B
Тогда задача линейного программирования будет иметь вид:
где
Слайд 73Найдем нижнюю и верхнюю цену игры:
α = 0, β =
Решим задачу для второго игрока В с помощью линейного программирования:
где
Решение:
Слайд 82Найдем нижнюю и верхнюю цену игры:
α = 4, β =
Решим задачу для второго игрока В с помощью линейного программирования:
где
Решение:
Слайд 90Игра с природой
- матричная игра, где игрок взаимодействует с окружающей
Слайд 91Игра с природой
Пусть A1 , A2, …, Am - возможные чистые
Платежная матрица:
Слайд 92Есть другой способ задания матрицы игры с природой – в виде
Риск rij игрока A при использовании стратегии Ai и состоянии природы Пj – разность между выигрышем, который получил бы игрок, если бы знал, что состоянием природы будет Пj, и выигрышем, который получит игрок, не зная этого.
Слайд 93Для определения оптимальной стратегии игрока A в игре с природой используется
Критерий Вальда – основан на выборе наилучшей из наихудших стратегий Ai.
Если в матрице А результат аij представляет выигрыш игрока A, при выборе его оптимальной стратегии используется максиминный критерий:
Слайд 94
Критерий Cэвиджа – использует матрицу рисков
В оптимальной стратегии минимизируется максимальный
Слайд 95
Критерий Гурвица – при любом выборе стратегии наихудший для игрока А
где α – показатель пессимизма (0 ≤ α ≤ 1).
Если аij – выигрыш игрока А, то оптимальной стратегией считается та, в которой достигается значение G:
Слайд 96
Критерий Лапласа – все состояния природы Пj, j = 1, …,
Оптимальной стратегией считается та, для которой достигается значение L:
Слайд 97Задача 9
Найти оптимальную стратегию игрока, используя критерии оптимальности Вальда,
Слайд 981. Найдем критерий Вальда.
В каждой строке матрицы
По критерию Вальда оптимальные стратегии A2 и A3.
Решение:
Слайд 992. Найдем критерий Сэвиджа.
Для матрицы А построим матрицу рисков R:
В каждом столбце выбираем наибольший элемент: 3; 4; 1
Слайд 100Найдем наибольший элемент каждой строки матрицы R, затем среди них выберем
По критерию Сэвиджа оптимальная стратегия A3.
Слайд 103
Ответ:
По критерию Вальда оптимальные стратегии A2 и A3.
По критерию
По критерию Гурвица оптимальная стратегия A3.
По критерию Лапласа оптимальная стратегия A3.
Слайд 104Задача 10
Найти оптимальную стратегию игрока, используя критерии оптимальности Вальда,
Слайд 1051. Найдем критерий Вальда.
В каждой строке матрицы
По критерию Вальда оптимальные стратегии A3.
Решение:
Слайд 1062. Найдем критерий Сэвиджа.
Для матрицы А построим матрицу рисков R:
В каждом столбце выбираем наибольший элемент: 8; 7; 9
Слайд 107Найдем наибольший элемент каждой строки матрицы R, затем среди них выберем
По критерию Сэвиджа оптимальная стратегия A3.
Слайд 110
Ответ:
По критерию Вальда оптимальная стратегия A3.
По критерию Сэвиджа оптимальная
По критерию Гурвица оптимальная стратегия A2.
По критерию Лапласа оптимальная стратегия A3.