Теория графов путь, цепь, цикл презентация

Содержание

ТЕОРИЯ ГРАФОВ ПУТЬ, ЦЕПЬ, ЦИКЛ Путь длины k – последовательность, содержащая k ребер. Длина пути - количество ребер в нем; каждое ребро считается столько раз, сколько оно встречается в маршруте.

Слайд 1ТЕОРИЯ ГРАФОВ ПУТЬ, ЦЕПЬ, ЦИКЛ
Путь (маршрут) – конечная последовательность ребер графа,

в котором два соседних ребра соединены общей вершиной. В маршруте одно и тоже ребро может встречаться несколько раз. Путь – это совокупность ребер, которые объединены вершинами таким образом, что можно двигаться по ним вдоль графа.
Обозначение маршрута – v0,v1,…vk.

Слайд 2ТЕОРИЯ ГРАФОВ ПУТЬ, ЦЕПЬ, ЦИКЛ
Путь длины k – последовательность, содержащая k

ребер. Длина пути - количество ребер в нем; каждое ребро считается столько раз, сколько оно встречается в маршруте.

Слайд 3ТЕОРИЯ ГРАФОВ ПУТЬ, ЦЕПЬ, ЦИКЛ
Путь называется простым или цепью, если все

его ребра различны. Если все вершины в цепи различны, то она является простой цепью.
Циклом называется путь, в котором v0=vk,.
Простой цикл – цикл, у которого все ребра и все вершины, кроме концов, различны.
В простой цепи число вершин на единицу больше, чем число ребер, а в простом цикле их количество совпадает.


Слайд 4ТЕОРИЯ ГРАФОВ ПУТЬ, ЦЕПЬ, ЦИКЛ
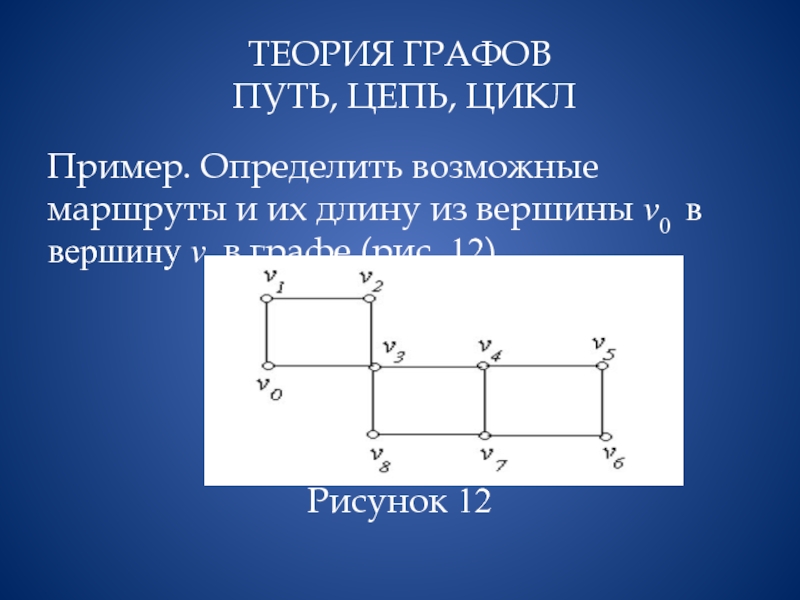
Пример. Определить возможные маршруты и их длину

из вершины v0 в вершину v8 в графе (рис. 12)




Рисунок 12

Слайд 5ТЕОРИЯ ГРАФОВ ПУТЬ, ЦЕПЬ, ЦИКЛ
Решение.
Пути:
1) v0v3v8 длиной 2;

5) v0v3v4v5v4v7v8 длиной 6;
2) v0v1v2v3v8 длиной 4; 6) v0v1v2v3v4v7v8 длиной 6;
3) v0v3v4v7v8 длиной 4; 7) v0v1v2v3v4v5v6v7v8 длиной 8;
4) v0v3v4v5v6v7v8 длиной 6;
8) v0v1v2v3v4v7v6v5v4v3v8 длиной 10.

Слайд 6ТЕОРИЯ ГРАФОВ ПУТЬ, ЦЕПЬ, ЦИКЛ
Маршрут v0v1v2v3v0 для графа (рис.

12) является простым циклом;
маршрут v3v4v5v6v7v4v3 является циклом, но не будет простым, потому что содержит повторяющиеся вершины.

Слайд 7ТЕОРИЯ ГРАФОВ ПУТЬ, ЦЕПЬ, ЦИКЛ
Эйлеров цикл – последовательность вер­шин (может быть

и с повторениями), через которые проходит иско­мый маршрут.
Цикл, проходящий через каждую вершину графа в точности один раз, называется гамильтоновым, а соответствующий
граф – гамилътоновым графом.

Слайд 8 ТЕОРИЯ ГРАФОВ СВЯЗНОСТЬ ГРАФА
Вершины v’ и v’’ называются связными, если существует маршрут

с началом в вершине v’ и концом в v’’. Граф называется связным, если любые пары его вершин связаны между собой.

Слайд 9ТЕОРИЯ ГРАФОВ СВЯЗНОСТЬ ГРАФА
Граф, изображенный на рис. 13 (a) – не связный,

а граф на рис. 13 (б) – связный.





Рисунок 13

Слайд 10ТЕОРИЯ ГРАФОВ КОЛИЧЕСТВО МАРШРУТОВ
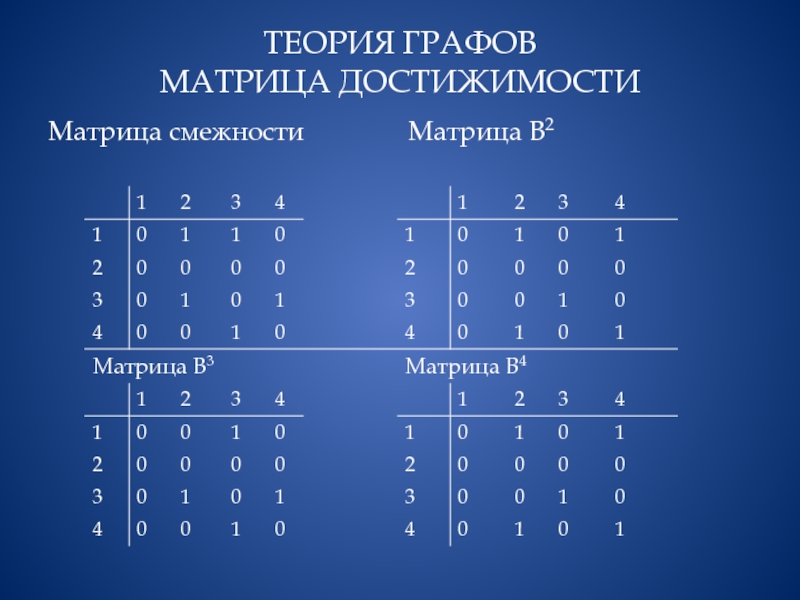
Для определения наличия маршрута между двумя вершинами используется матрица

смежности. Булево произведение матрицы В с самой собой обозначается через В2. В этой матрице 1 символизирует наличие пути
длины 2. По матрице В3 = В * В * В можно определить все пути длины 3, т.е., матрица Вk хранит сведения о путях длины к.



Слайд 11ТЕОРИЯ ГРАФОВ КОЛИЧЕСТВО МАРШРУТОВ
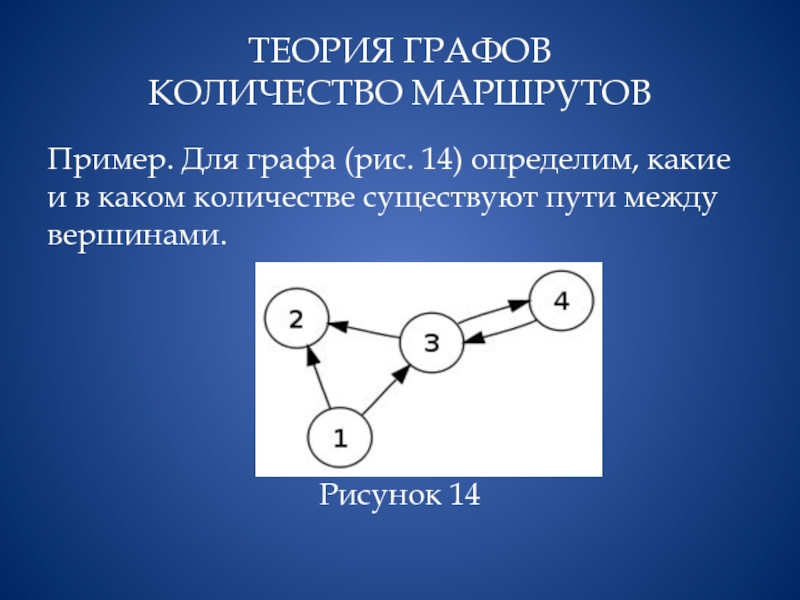
Пример. Для графа (рис. 14) определим, какие и в

каком количестве существуют пути между вершинами.





Рисунок 14

Слайд 12ТЕОРИЯ ГРАФОВ ОСНОВНЫЕ ПОНЯТИЯ
Матрица смежности Матрица В2

Слайд 13ТЕОРИЯ ГРАФОВ ОСНОВНЫЕ ПОНЯТИЯ
Матрица В3 Матрица В4

Слайд 14ТЕОРИЯ ГРАФОВ КОЛИЧЕСТВО МАРШРУТОВ
При использовании алгебраических операций получаем матрицу,




которая характеризует не только

наличие путей между вершинами, но и количество таких путей.

Слайд 15ТЕОРИЯ ГРАФОВ КОЛИЧЕСТВО МАРШРУТОВ
 

Слайд 16ТЕОРИЯ ГРАФОВ КОЛИЧЕСТВО МАРШРУТОВ
 

Слайд 17ТЕОРИЯ ГРАФОВ КОЛИЧЕСТВО МАРШРУТОВ
 

Слайд 18ТЕОРИЯ ГРАФОВ МАТРИЦА ДОСТИЖИМОСТИ
Матрица достижимости ориентированного графа – бинарная матрица замыкания по

транзитивности. Таким образом, в матрице достижимости хранится информация о существовании путей между вершинами орграфа.

Слайд 19ТЕОРИЯ ГРАФОВ МАТРИЦА ДОСТИЖИМОСТИ
Для нахождения матрицы достижимости начинаем работу с построения матрицы

смежности.
Находим булевы степени этой матрицы: В2, В3, …, Вn
Находим матрицу достижимости:
В*=В∨В2 ∨ … ∨ Вn







Слайд 20ТЕОРИЯ ГРАФОВ МАТРИЦА ДОСТИЖИМОСТИ
Матрица смежности Матрица В2

Слайд 21ТЕОРИЯ ГРАФОВ МАТРИЦА ДОСТИЖИМОСТИ
Бо­лее удобный путь определения матрицы достижимости дает так

называемый алгоритм Уоршелла (алгоритм Флойда  – Уоршелла)   – алгоритм для нахождения расстояний между всеми вершинами орграфа. Разработан в 1962 году Робертом Флойдом и Стивеном Уоршеллом.

Слайд 22ТЕОРИЯ ГРАФОВ МАТРИЦА ДОСТИЖИМОСТИ
Алгоритм Уоршелла генерирует последовательность матриц W0…Wn, матрица
W0 совпадает

с матрицей смежности орграфа, а Wn – искомая матрица достижимости.




Слайд 23ТЕОРИЯ ГРАФОВ АЛГОРИТМ УОРШЕЛЛА
Берем k-ый столбец матрицы Wk-1
Строку с номером i(i=1,…,n), у

которой на k-ом месте стоит 0, переписываем в i-ую строку марицы Wk .
Строку с номером i(i=1,…,n), у которой на k-ом месте стоит 1, объединяем с помощью операции или с k-ой строкой, а результат записываем в
i-ую строку марицы Wk .

Слайд 24ТЕОРИЯ ГРАФОВ АЛГОРИТМ УОРШЕЛЛА
 

Слайд 25ТЕОРИЯ ГРАФОВ АЛГОРИТМ УОРШЕЛЛА
 

Слайд 26ТЕОРИЯ ГРАФОВ АЛГОРИТМ УОРШЕЛЛА
 

Слайд 27ТЕОРИЯ ГРАФОВ АЛГОРИТМ УОРШЕЛЛА
 

Слайд 28ТЕОРИЯ ГРАФОВ АЛГОРИТМ УОРШЕЛЛА
 

Похожие презентации

Задачи с параметром в материалах Государственной итоговой аттестации и методы их решения (По материалам ЕГЭ за последние 5лет) 266
Алгебра. Лекция 6. Классы вычетов 498
Понятие управления 777
Метод наименьших квадратов 259
Иррациональные числа. История открытия 529
Модуль числа 315

Обратная связь

Если не удалось найти и скачать презентацию, Вы можете заказать его на нашем сайте. Мы постараемся найти нужный Вам материал и отправим по электронной почте. Не стесняйтесь обращаться к нам, если у вас возникли вопросы или пожелания:

Email: Нажмите что бы посмотреть 

Что такое ThePresentation.ru?

Это сайт презентаций, докладов, проектов, шаблонов в формате PowerPoint. Мы помогаем школьникам, студентам, учителям, преподавателям хранить и обмениваться учебными материалами с другими пользователями.

Для правообладателей

Яндекс.Метрика