- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Теория графов презентация
Содержание
- 1. Теория графов
- 2. Литература В.А. Горбатов Дискретная математика М.: АСТ;
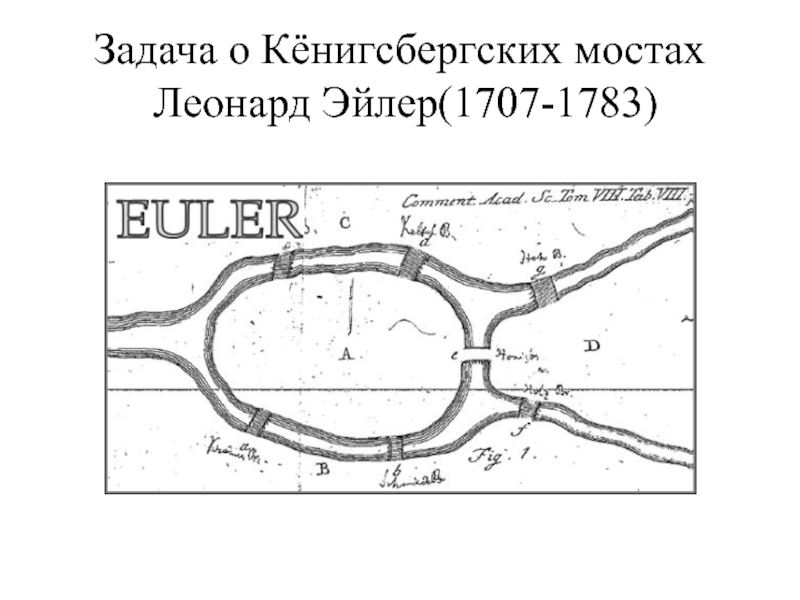
- 3. Задача о Кёнигсбергских мостах Леонард Эйлер(1707-1783)
- 4. Основные объекты графов носитель метаграфа
- 5. Понятие графа и орграфа Граф G=, где
- 6. Неориентированный граф (граф) G = ,
- 7. Ориентированный граф (орграф) G=, V={v1,v2,…,vn},n≥1
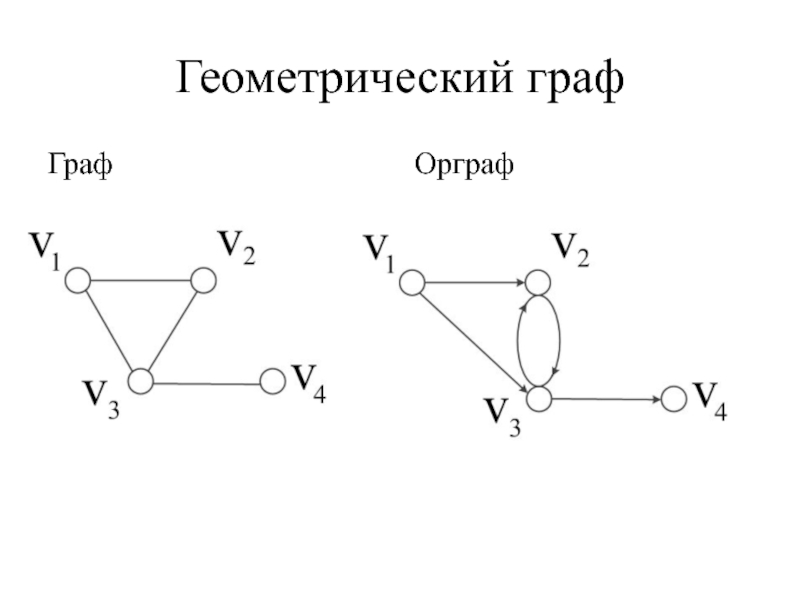
- 8. Геометрический граф Граф Орграф
- 9. Обозначение Gp,q ⏐V⏐= p, ⏐U⏐= q G1,0 - тривиальный граф
- 10. типы метаграфов ГИПЕРГРАФ (модельный граф) Сигнатура
- 11. взвешенные метаграфы f: V→N - весовая
- 12. Локальная структура графа (vi,vj)∈U – vi и
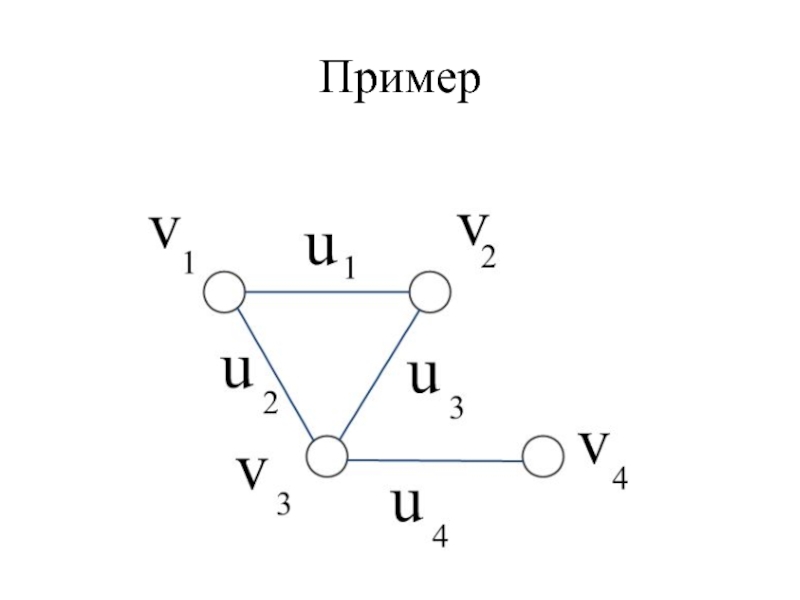
- 13. Пример
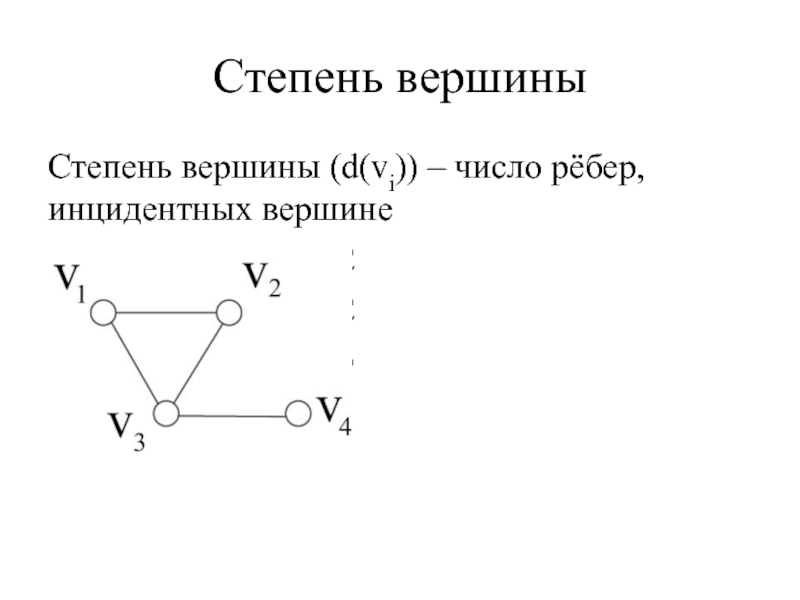
- 14. Степень вершины Степень вершины (d(vi)) – число рёбер, инцидентных вершине d(v1)=2 d(v2)=2 d(v3)=3 d(v4)=1
- 15. Теорема В любом конечном графе число вершин нечётной степени чётно.
- 16. Свойства степеней графа Gp,q
- 17. Степень графа Степень графа (максимальная степень вершины) Минимальная степень вершины графа
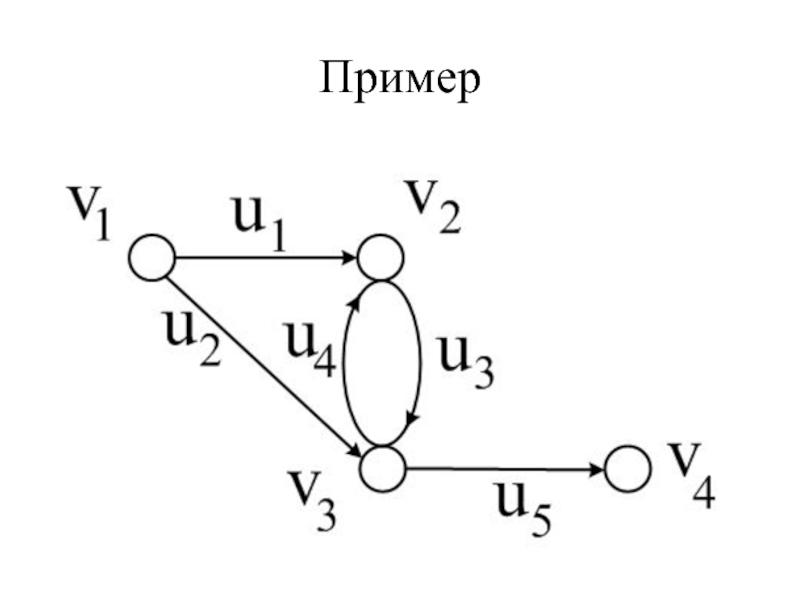
- 18. Локальная структура ориентированного графа uk= (vi,vj) –
- 19. Пример
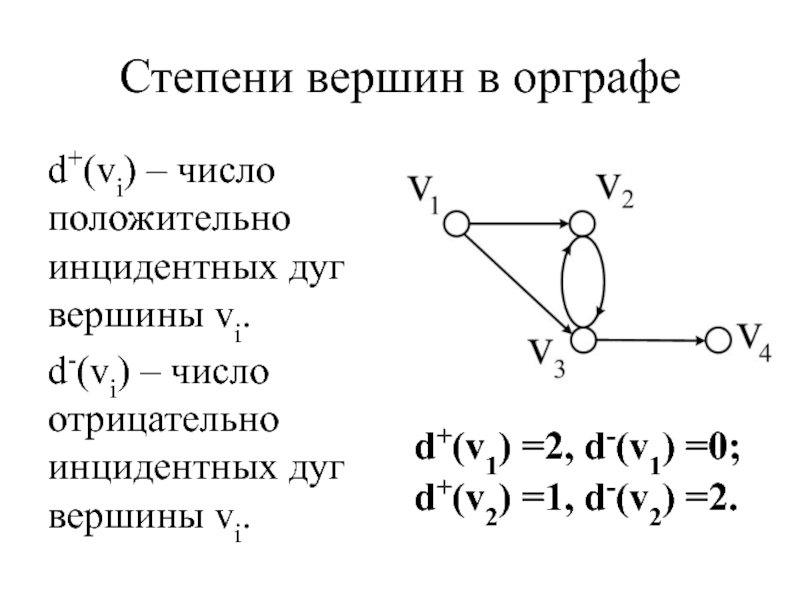
- 20. Степени вершин в орграфе d+(vi) – число
- 21. Свойства степеней орграфа Для любого ориентированного графа
- 22. Свойства степеней орграфа Для любого ориентированного графа
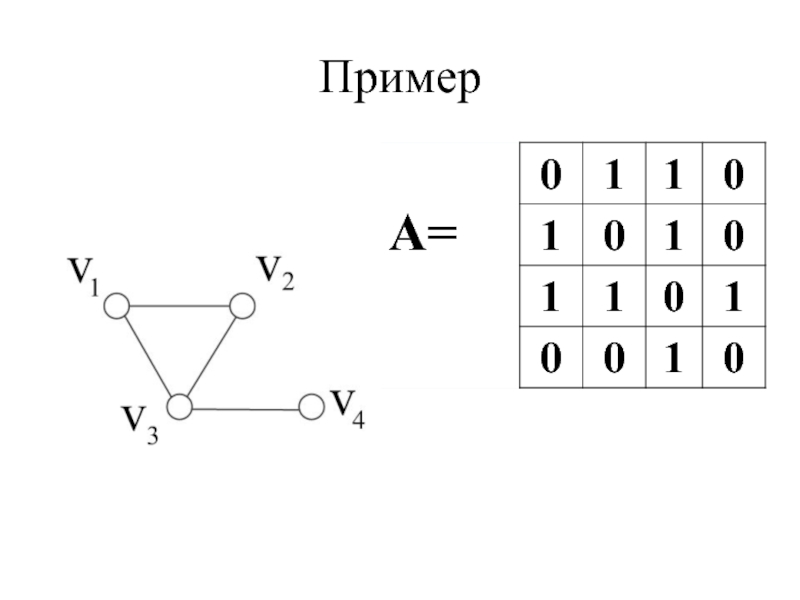
- 23. Матричное представление графа Матрица смежности А:
- 24. Пример
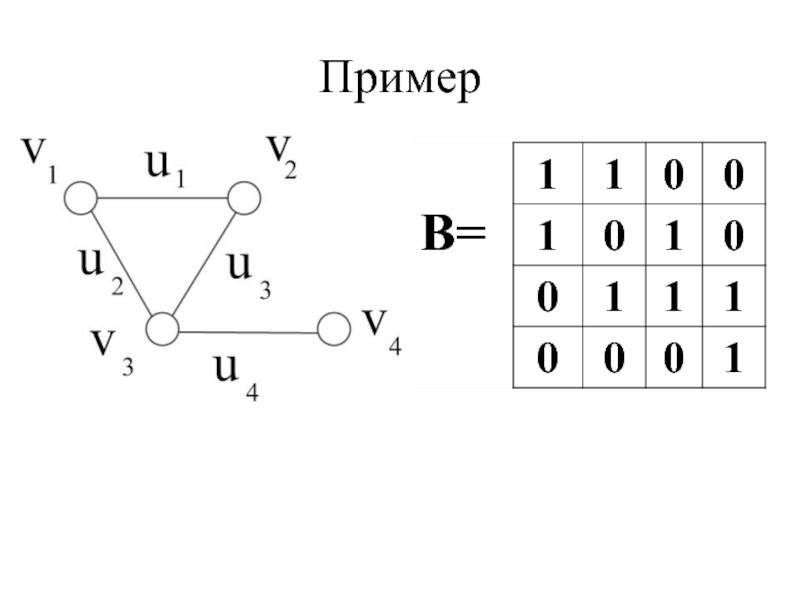
- 25. Матрица инцидентности В
- 26. Пример
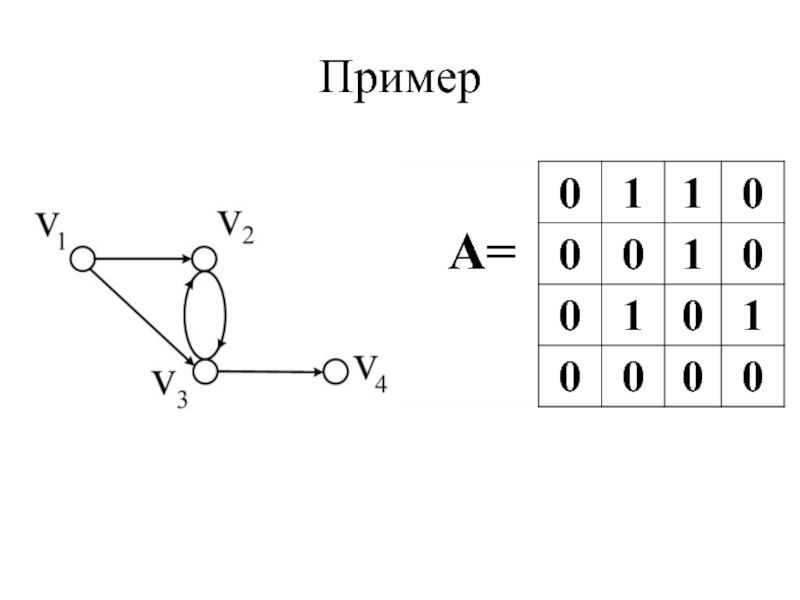
- 27. Матрица смежности орграфа А:
- 28. Пример
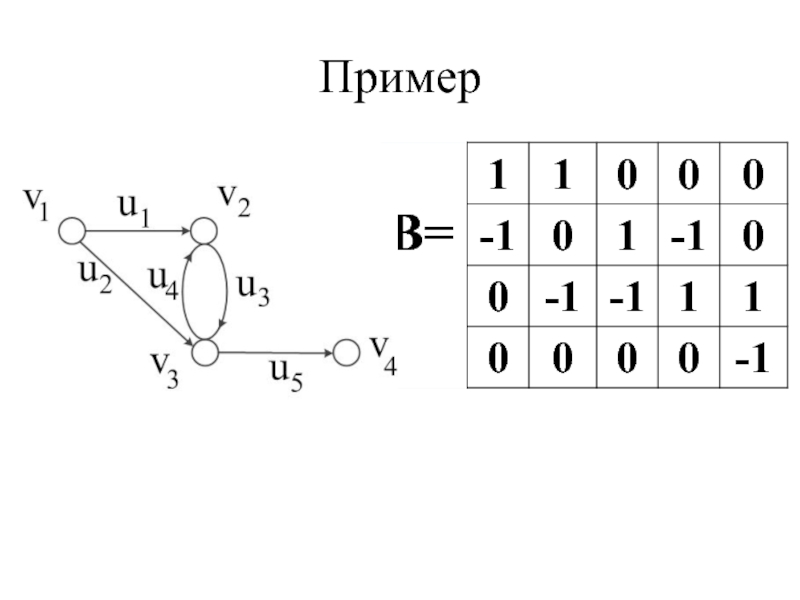
- 29. Матрица инцидентности В
- 30. Пример
- 31. Функциональный способ задания графов G= Г- функция
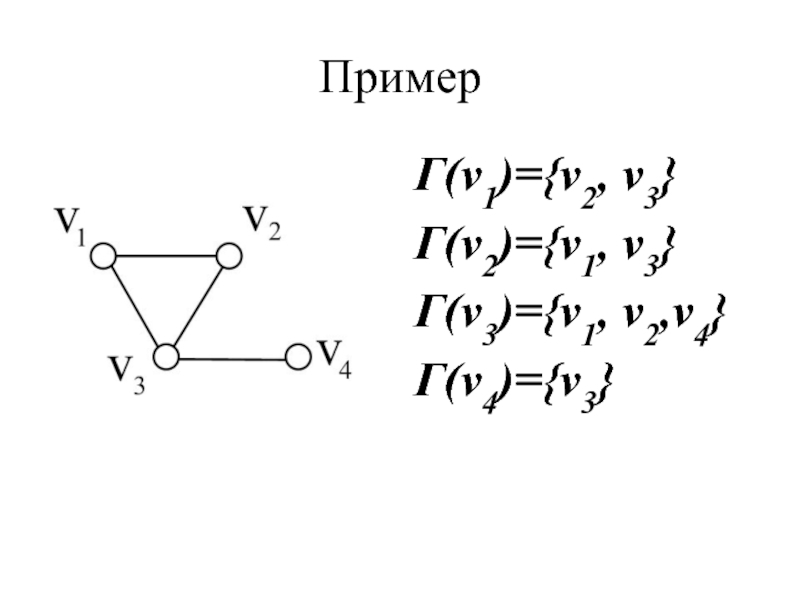
- 32. Пример Г(v1)={v2, v3} Г(v2)={v1, v3} Г(v3)={v1, v2,v4} Г(v4)={v3}
- 33. Функциональный способ задания орграфов G= G=
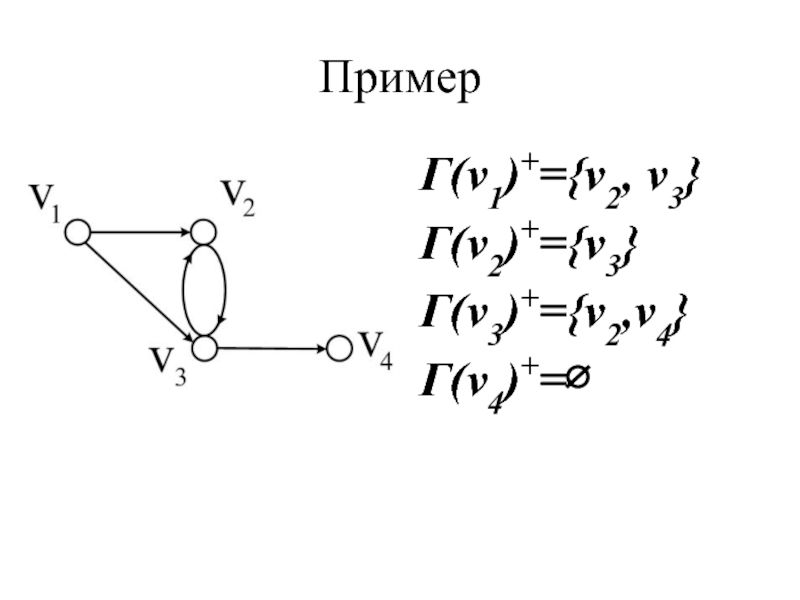
- 34. Пример Г(v1)+={v2, v3} Г(v2)+={v3} Г(v3)+={v2,v4} Г(v4)+=∅
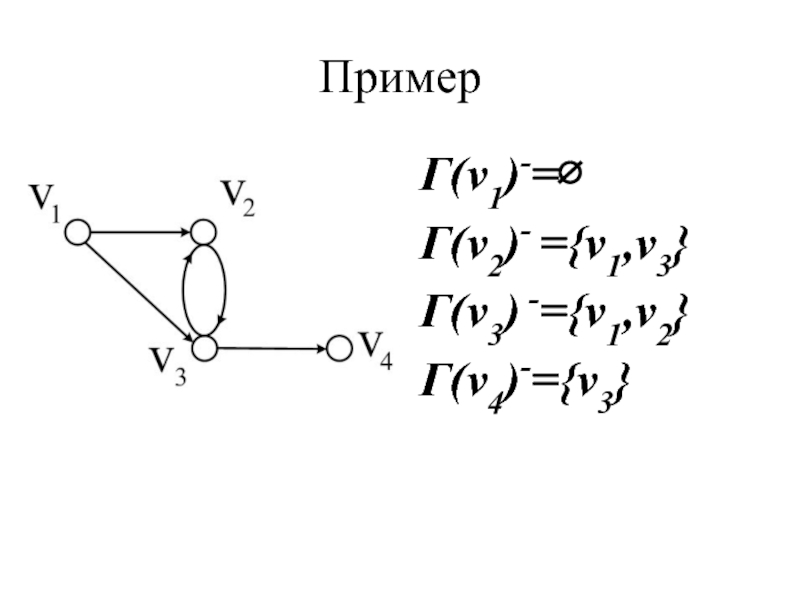
- 35. Пример Г(v1)-=∅ Г(v2)- ={v1,v3} Г(v3) -={v1,v2} Г(v4)-={v3}
- 36. Изоморфизм графов Графы изоморфны, если существует взаимно однозначное соответствие между множествами вершин, сохраняющее отношение смежности
- 37. Функциональное задание изоморфизма графов Два графа Ga=〈Va,Ua〉
- 38. Свойства изоморфизма Отношение рефлексивно симметрично транзитивно Эквивалентность
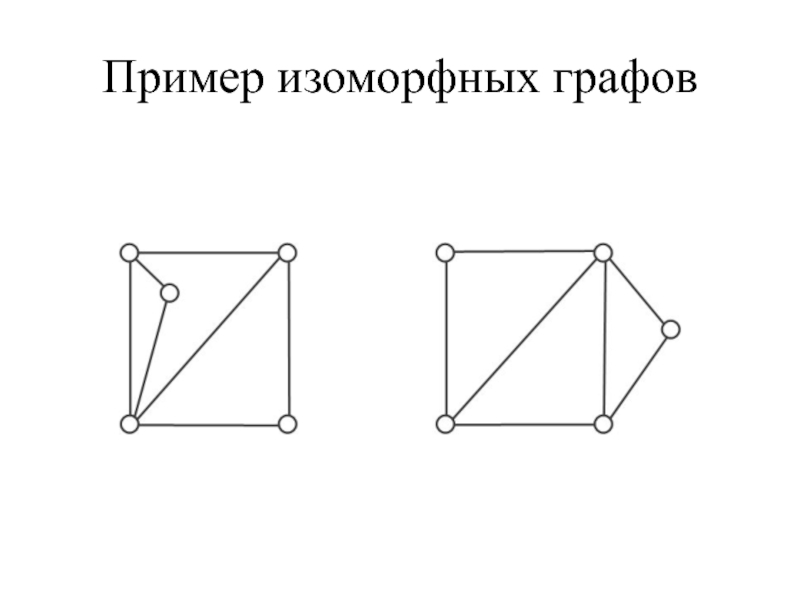
- 39. Пример изоморфных графов
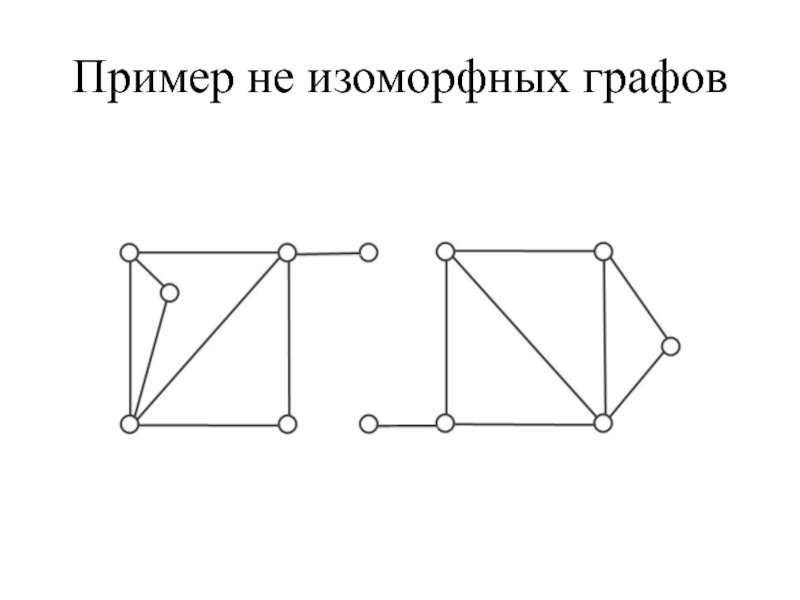
- 40. Пример не изоморфных графов
- 41. Инварианты графа Количественная или качественная характеристики,
- 42. Полный граф Kn Граф полный, если
- 43. Двудольный граф Граф двудольный, если множество вершин
- 44. Двудольные графы. Примеры
- 45. Полный двудольный граф Km,n Km,n - граф
- 46. Полные двудольные графы Km,n
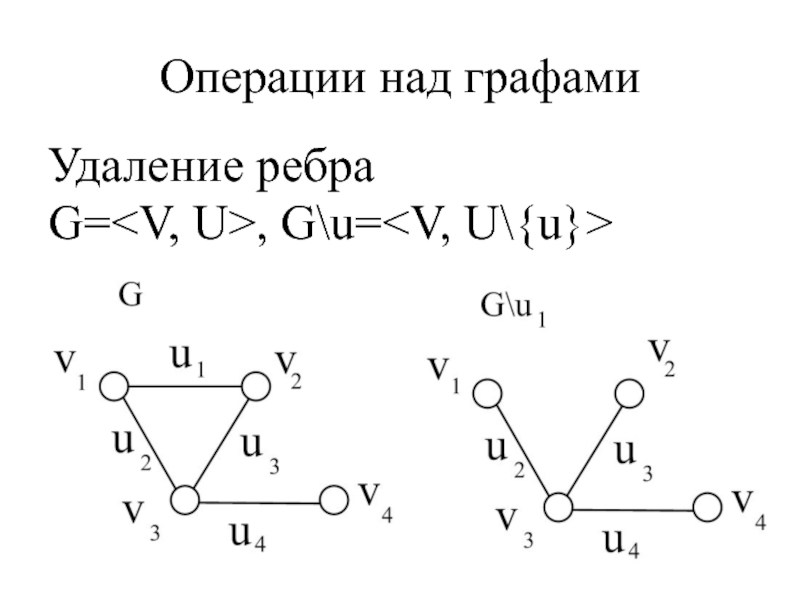
- 47. Операции над графами Удаление ребра G=, G\u=
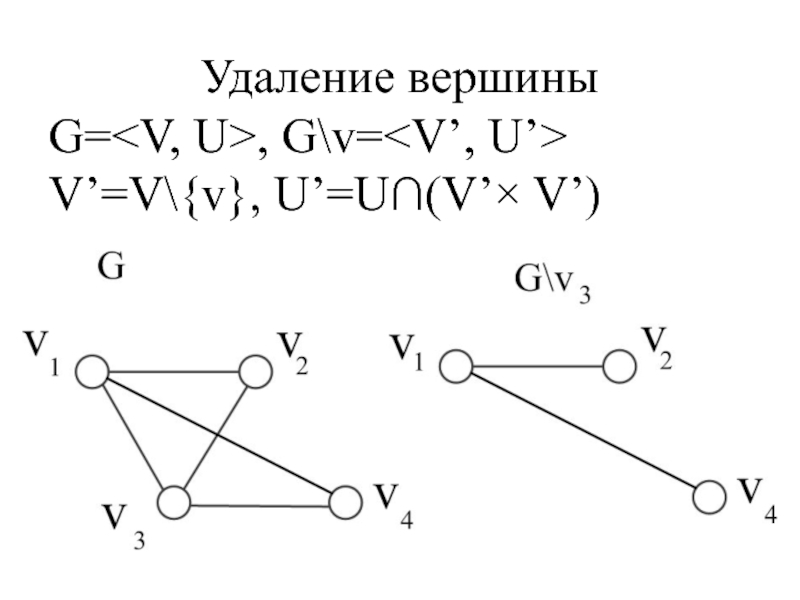
- 48. Удаление вершины G=, G\v= V’=V\{v}, U’=U∩(V’× V’)
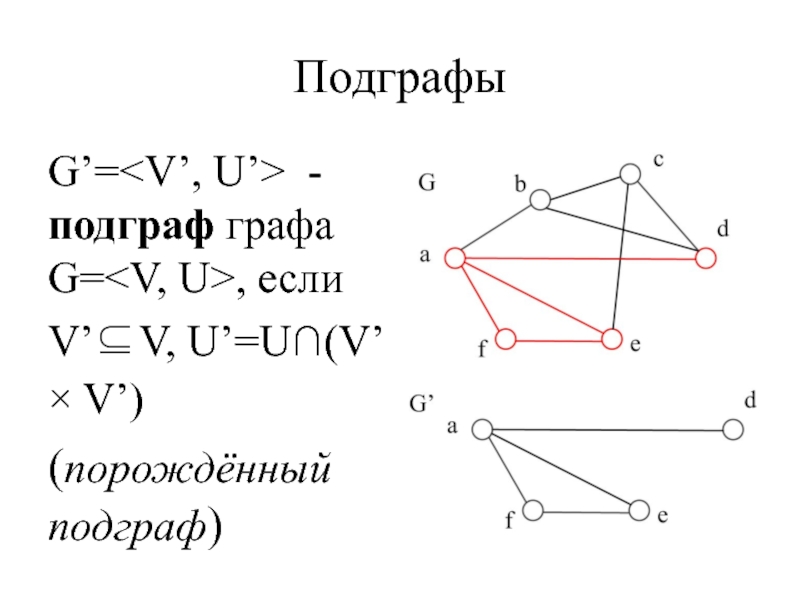
- 49. Подграфы G’= - подграф графа G=, если
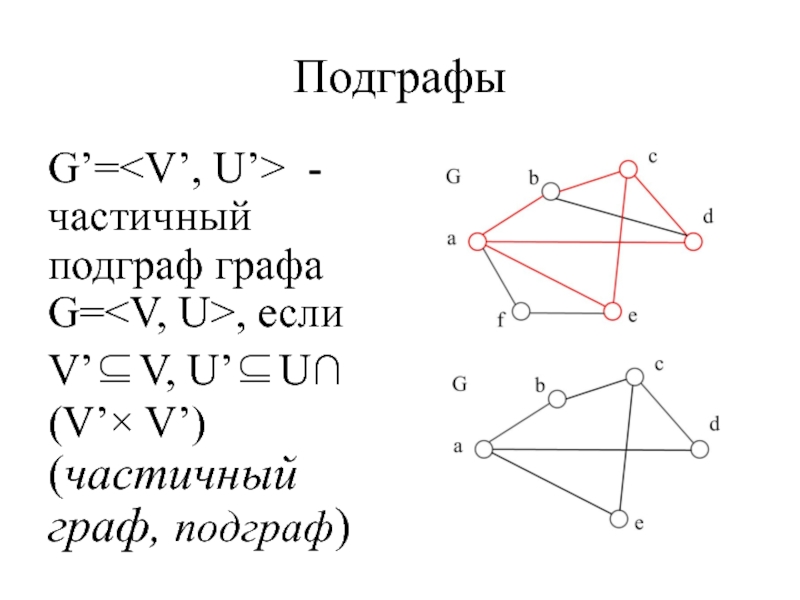
- 50. Подграфы G’= - частичный подграф графа G=,
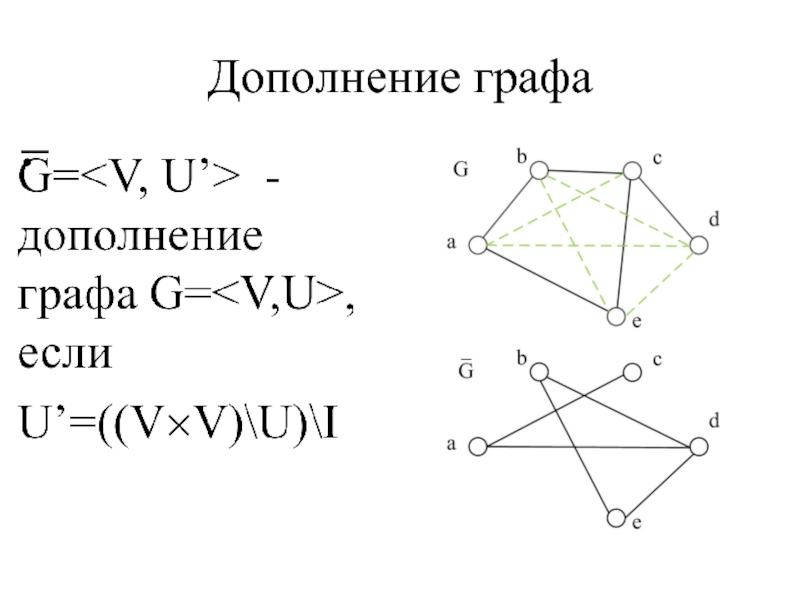
- 51. Дополнение графа
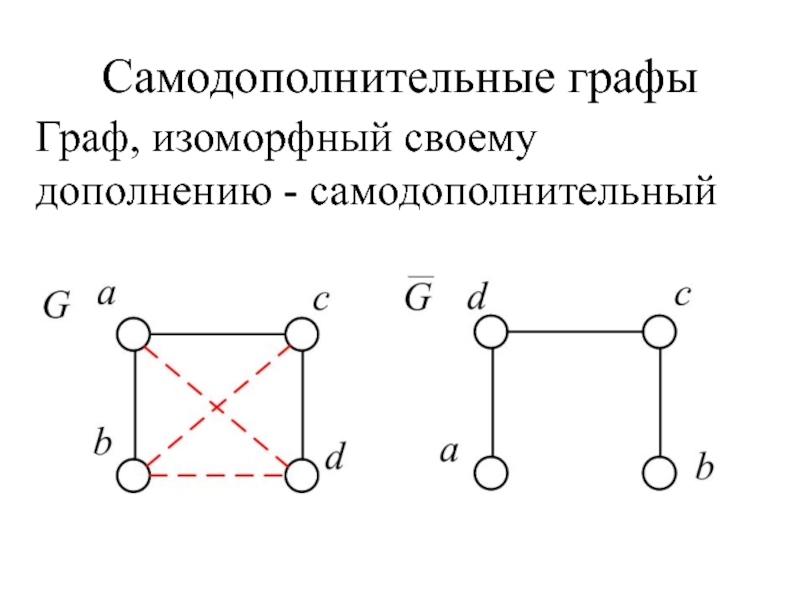
- 52. Самодополнительные графы Граф, изоморфный своему дополнению - самодополнительный
Слайд 2Литература
В.А. Горбатов Дискретная математика М.: АСТ; Астрель, 2003
Харари Ф. Теория
графов, 2003г
Кристофидес, Н. Теория графов. Алгоритмический подход. 1978
Кузнецов О.П., Дискретная математика для инженера, 2009.
Тихомирова А.Н. Теория графов, МИФИ,
Кристофидес, Н. Теория графов. Алгоритмический подход. 1978
Кузнецов О.П., Дискретная математика для инженера, 2009.
Тихомирова А.Н. Теория графов, МИФИ,
Слайд 4Основные объекты графов
носитель метаграфа (конечное множество вершин). V={v1,v2, …
vp}
сигнатура метаграфа (конечное множество связей между вершинами). U={u1,u2, … uq}
сигнатура метаграфа (конечное множество связей между вершинами). U={u1,u2, … uq}
©П.Порешин
Слайд 5Понятие графа и орграфа
Граф G=, где
V={v1,v2,…,vn}, n≥1 – множество вершин
(носитель),
U⊆V×V (сигнатура).
U⊆V×V (сигнатура).
Слайд 6Неориентированный граф (граф)
G = ,
V = {v1,v2,…,vn},n≥1,
U⊆V×V
(vi,vj)
= (vj, vi)
(vi,vj) – ребро графа
(vi, vi) - петля
(vi,vj) – ребро графа
(vi, vi) - петля
Слайд 10типы метаграфов
ГИПЕРГРАФ (модельный граф)
Сигнатура (U) - множество граней, каждая из
которых связывает некоторое подмножество вершин. Грань – подмножество вершин гиперграфа
©П.Порешин
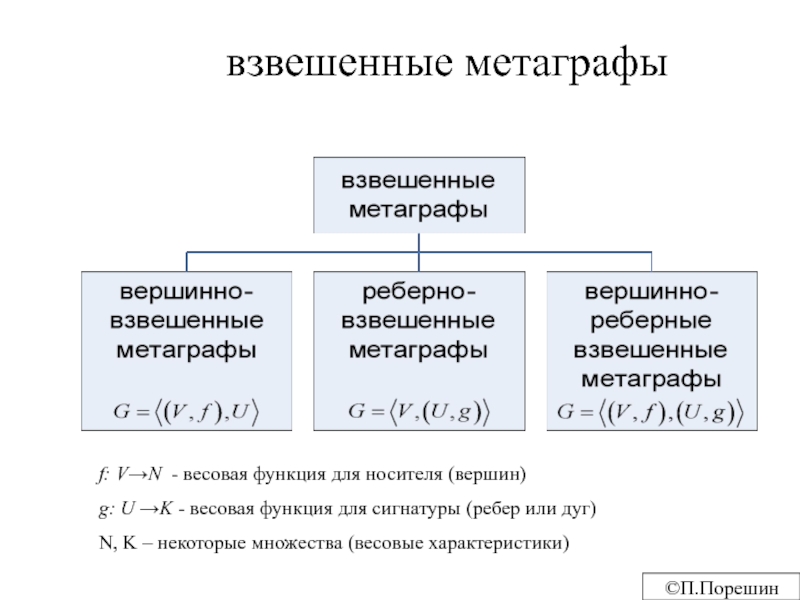
Слайд 11взвешенные метаграфы
f: V→N - весовая функция для носителя (вершин)
g: U
→K - весовая функция для сигнатуры (ребер или дуг)
N, K – некоторые множества (весовые характеристики)
N, K – некоторые множества (весовые характеристики)
©П.Порешин
Слайд 12Локальная структура графа
(vi,vj)∈U – vi и vj – смежны
uk= (vi,vj) –
uk инцидентно vi,
uk инцидентно vj, vi инцидентно uk
vj инцидентно uk
uk= (vi,vj), un= (vi,vm) –
uk и un – смежны
uk инцидентно vj, vi инцидентно uk
vj инцидентно uk
uk= (vi,vj), un= (vi,vm) –
uk и un – смежны
Слайд 14Степень вершины
Степень вершины (d(vi)) – число рёбер, инцидентных вершине
d(v1)=2
d(v2)=2
d(v3)=3
d(v4)=1
Слайд 18Локальная структура ориентированного графа
uk= (vi,vj) – дуга uk положительно инцидентна vi,
дуга
uk отрицательно инцидентна vj,
uk= (vi,vj), un= (vi,vm) –
uk и un – смежны
uk= (vi,vj), un= (vi,vm) –
uk и un – смежны
Слайд 20Степени вершин в орграфе
d+(vi) – число положительно инцидентных дуг вершины vi.
d-(vi) – число отрицательно инцидентных дуг вершины vi.
d+(v1) =2, d-(v1) =0;
d+(v2) =1, d-(v2) =2.
Слайд 31Функциональный способ задания графов
G=
Г- функция окрестности вершин
Г:V→P(V)
Г(v)={vi ⎢ vi
смежна с v}
Слайд 33Функциональный способ задания орграфов
G= G=
Г+, Г- - функции положительной и
отрицательной полуокрестности вершины, соответственно
Слайд 36Изоморфизм графов
Графы изоморфны, если существует взаимно однозначное соответствие между множествами вершин,
сохраняющее отношение смежности
Слайд 37Функциональное задание изоморфизма графов
Два графа Ga=〈Va,Ua〉 и Gb=〈Vb,Ub〉 изоморфны, если существует
взаимно однозначная функция
h: Va→Vb такая, что: 1) если (va1 ,va2 )∈ Ua, то (h(va1),h(va2)) ∈ Ub; 2) если (vb1,vb2) ∈ Ub, то (h-1(vb1),h-(vb2)) ∈ Ua
h: Va→Vb такая, что: 1) если (va1 ,va2 )∈ Ua, то (h(va1),h(va2)) ∈ Ub; 2) если (vb1,vb2) ∈ Ub, то (h-1(vb1),h-(vb2)) ∈ Ua
Слайд 41Инварианты графа
Количественная или качественная характеристики, неизменные для всех изоморфных между
собой графов (орграфов) называется ИНВАРИАНТОМ
Поиск полной системы инвариантов графа, задающей граф с точность до изоморфизма – основная задача теории графов
(полная система инвариантов ещё не найдена)
(полная система инвариантов ещё не найдена)
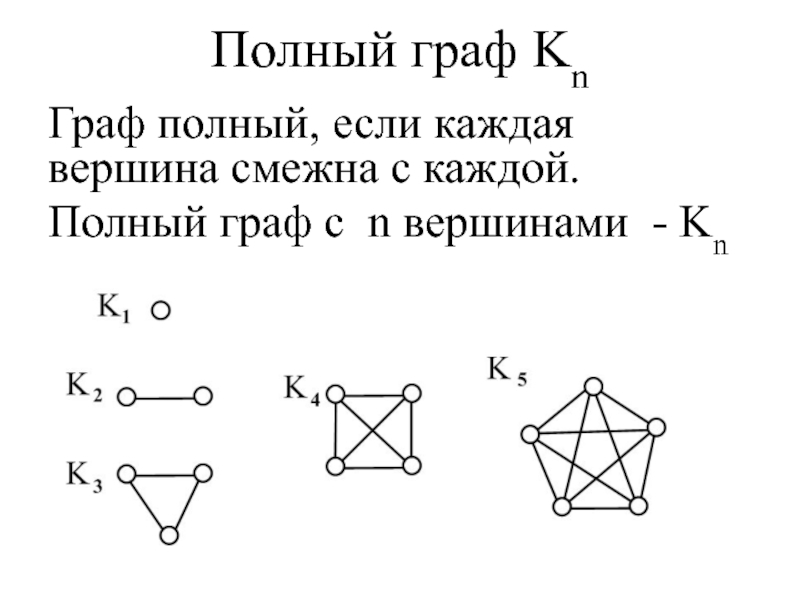
Слайд 42Полный граф Kn
Граф полный, если каждая вершина смежна с каждой.
Полный граф
с n вершинами - Kn
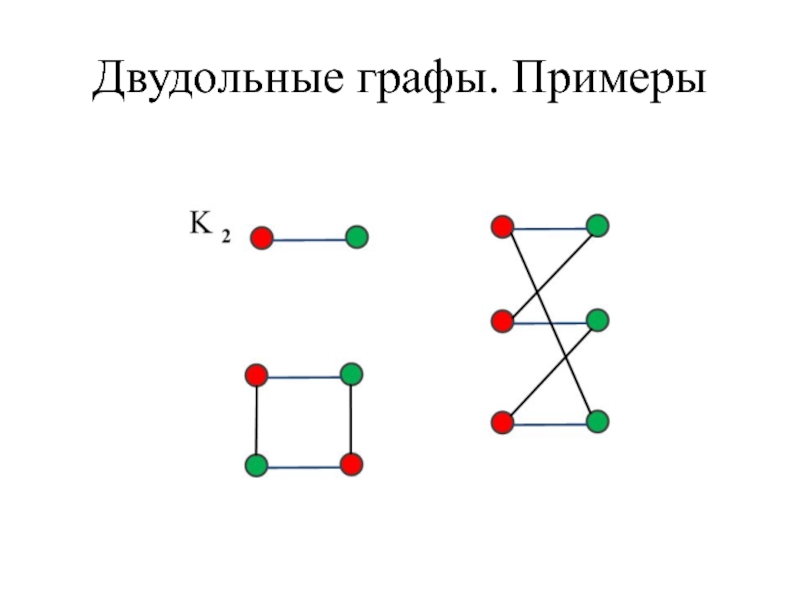
Слайд 43Двудольный граф
Граф двудольный, если множество вершин графа можно разбить на два
непересекающихся подмножества, в каждом из которых никакая пара вершин не смежна.
G=, V=V1∪V2, V1∩V2=∅, U⊆V1×V2
G=
Слайд 45Полный двудольный граф Km,n
Km,n - граф двудольный и каждая вершина из
множества V1 смежна с каждой вершиной из V2, ⎜V1⎜=m, ⎜V2⎜=n.
G=, V=V1∪V2, V1∩V2=∅, U=V1×V2
G=
Слайд 50Подграфы
G’= - частичный подграф графа G=, если
V’⊆V, U’⊆U∩(V’×
V’) (частичный граф, подграф)