- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Методи вирішення нелінійних рівнянь. (Лекція 3) презентация
Содержание
- 1. Методи вирішення нелінійних рівнянь. (Лекція 3)
- 2. Наближене рішення нелінійних рівнянь. Групи методів:
- 3. Метод половинного ділення Постановка задачі. Дано нелінійне
- 4. Метод половинного ділення (продовження) Де
- 5. Метод ітерації Постановка задачі. Дано нелінейне рівняння,
- 6. Метод ітерації (продовження) диферинцюєма на даному відрізку
- 7. Метод хорд При вирішенні нелінійного рівняння методом
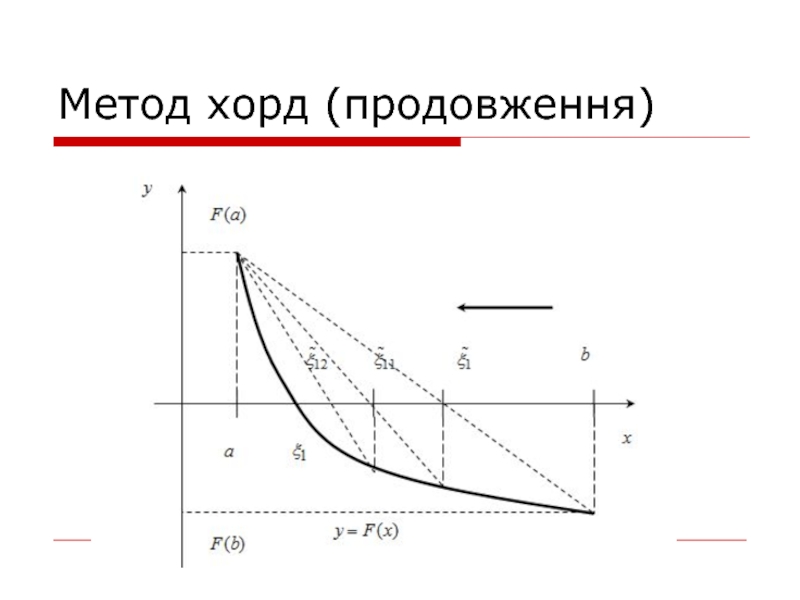
- 8. Метод хорд (продовження)
- 9. Метод дотичних При вирішенні нелінійного рівняння методом
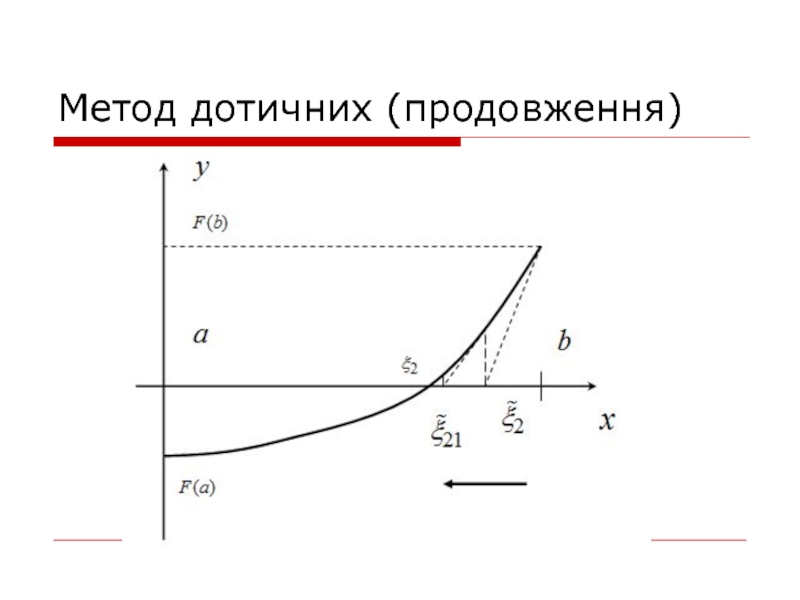
- 10. Метод дотичних (продовження)
Слайд 2Наближене рішення нелінійних рівнянь.
Групи методів:
Метод половинного ділення, хорд, метод дотичних,
комбінований метод
Метод ітерації
Методи відділення ізольованих коренів рівняння
Метод ітерації
Методи відділення ізольованих коренів рівняння
Слайд 3Метод половинного ділення
Постановка задачі. Дано нелінійне рівняння
, де функція визначена і неперервна для всіх , при чому функція змінює знак на кінцях цього відрізку, тобто
Знайти наближений розв'язок даного рівняння
з точністю , а так само необхідне для цього число розбиття відрізка . Наближене рішення і похибка наближення знаходяться за наступною схемою:
Знайти наближений розв'язок даного рівняння
з точністю , а так само необхідне для цього число розбиття відрізка . Наближене рішення і похибка наближення знаходяться за наступною схемою:
Слайд 4Метод половинного ділення (продовження)
Де
задовольняє умовам:
з останнього визначається число розбиття відрізка
з останнього визначається число розбиття відрізка
Слайд 5Метод ітерації
Постановка задачі. Дано нелінейне рівняння, де функція
визначена та неперервно-диференціюєма для всіх , при чому функція змінює знак на кінцях цього відрізку, тобто
Знайти наближене рішення даного рівняння з точністю .
Наближене рішення та похибка наближення знаходяться за наступною схемою:
Рівняння приводиться до виду , де функція задовольняє умовам:
Знайти наближене рішення даного рівняння з точністю .
Наближене рішення та похибка наближення знаходяться за наступною схемою:
Рівняння приводиться до виду , де функція задовольняє умовам:
Слайд 6Метод ітерації (продовження)
диферинцюєма на даному відрізку та
При вирішенні нелінійного рівняння методом
ітерацій скористуємся записом рівняння в вигляді x=f(x). Задаються початкове значення аргумента x0 та точність ε. Перше наближення рішення x1 знаходимо з выразу x1=f(x0), друге - x2=f(x1) і т.д. В загальному випадку (i+1)-е наближання знайдемо за формулою xi+1 =f(xi). Цю процедуру повторюємо поки |f(xi)|>ε. Умова сходимості метода ітерацій |f'(x)|<1.
Слайд 7Метод хорд
При вирішенні нелінійного рівняння методом хорд задається інтервал [a,b], на
якому існує тільки одно рішення і точність ε. Потім через дві точки з координатами (a,F(a)) і (b,F(b)) проводимо відрізок прямої лінії (хорду) та визначити точку перетину цієї лінії з віссю абсцис (точка c). Якщо при цьому F(a)∙F(c)<0, то праву межу інтервалу переносимо в точку с (b=c). Якщо указана умова не виконується, то в точку c переноситься ліва межа інтервалу (а=с). Пошук рішення припиняється при досягненні заданої точності |F(c)|< ε. Для визначення точки перетину хорди з віссю абсцис скористуємося наступною формулою
Слайд 9Метод дотичних
При вирішенні нелінійного рівняння методом дотичних задаються початковее значення аргументу
x0 та точність ε. Потім в точці (x0,F(x0)) проводимо дотичну до графіку F(x) і визначимо точку перетину дотичну з віссю абсцис x1. В точці (x1,F(x1)) знову будуємо дотичну, знаходимо наступне наближення шукомого рішення x2 та ін. Вказану процедуру повторюємо доки |F(xi)| > ε. Для визначення точки перетину (i+1) дотичної з віссю абсцис скористуємося наступною формулою.
Умова сходимості методу дотичних F(x0)∙F''(x0)>0.
Умова сходимості методу дотичних F(x0)∙F''(x0)>0.






![Метод хордПри вирішенні нелінійного рівняння методом хорд задається інтервал [a,b], на якому існує тільки одно](/img/tmb/5/482772/da7f8fc7177230f27a0c95114248bef5-800x.jpg)