Теоремы о пределах функции и о непрерывных функциях. Асимптотические приближения. Точки разрыва. (Лекция 4) презентация

Основные теоремы о непрерывных функциях. Точки разрыва. Классификация точек разрыва.
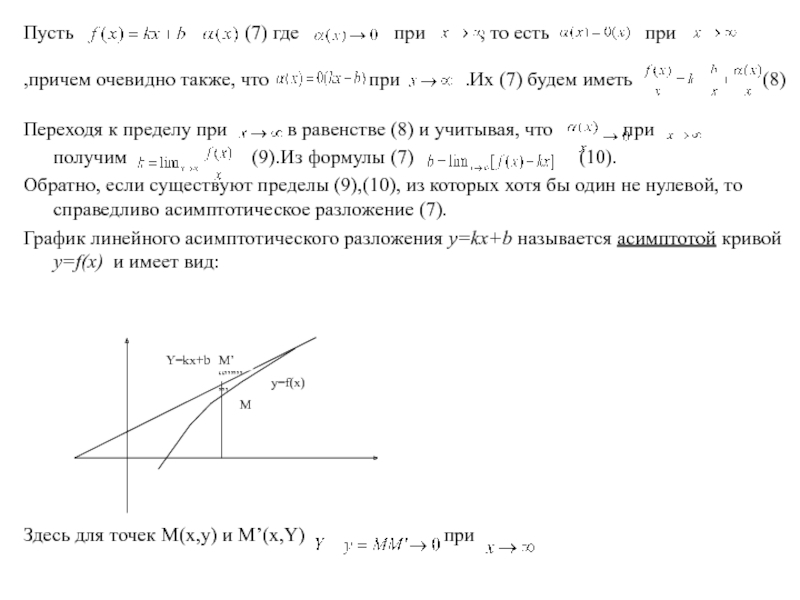
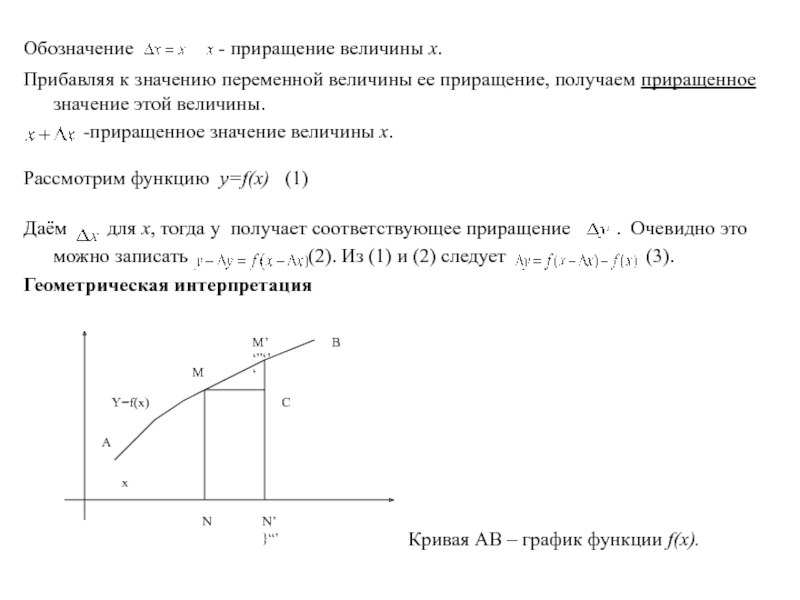
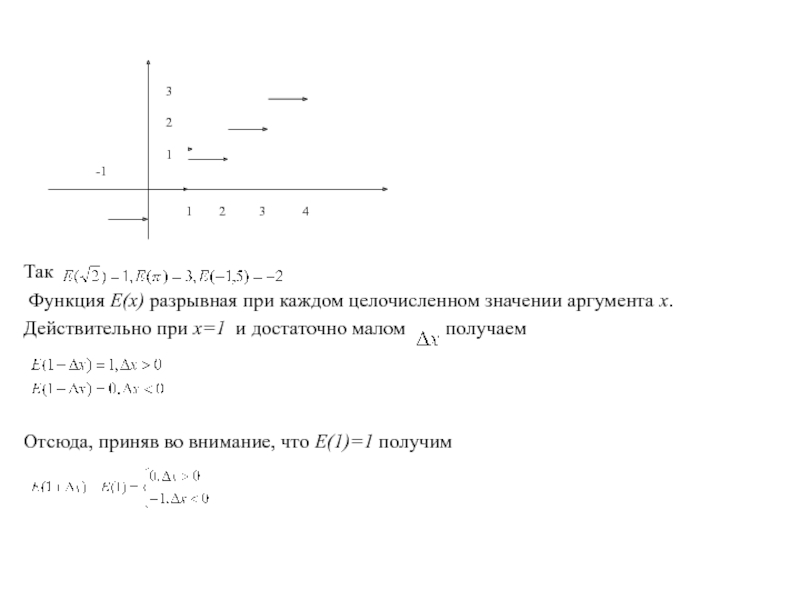
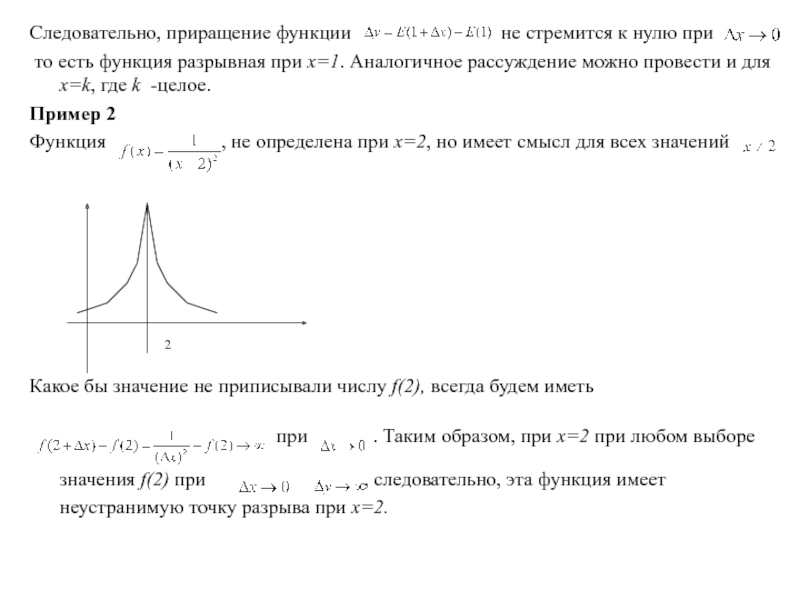
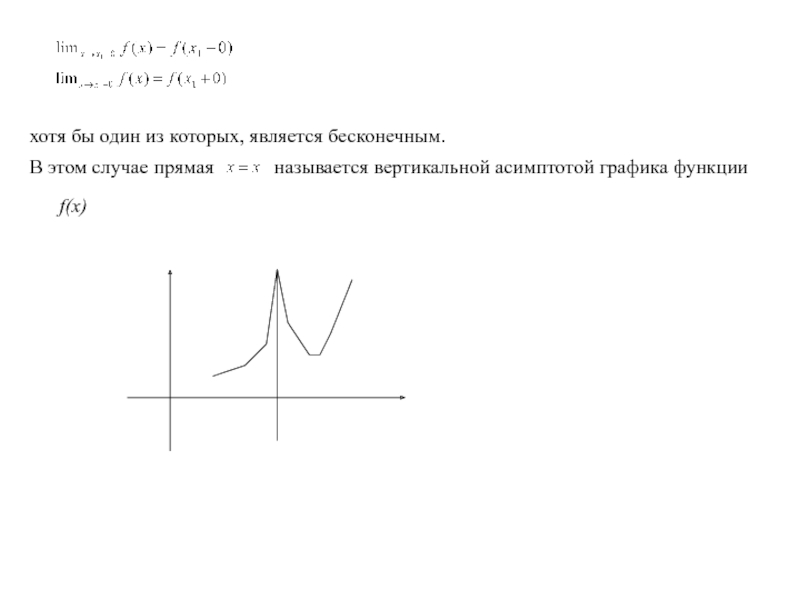
Основные теоремы о пределах

Предполагается, что функции, рассматриваемые в следующих теоремах определены на некотором общем множестве Х, для которого точка а является предельной точкой.
Теорема 1
Если каждое слагаемое алгебраической суммы конечного числа функций имеет предел при , то предел этой алгебраической суммы при существует и равен такой же алгебраической сумме пределов слагаемых.
Доказательство
Рассмотрим алгебраическую сумму трех функций f(x)+g(x)-h(x), где

Так как функции отличаются от своих пределов на бесконечно малые, то получаем , (1), где при Из равенств (1), используя теорему об алгебраической сумме бесконечно малых будем иметь
(2), где при

бесконечно малую функцию и следовательно, это число является пределом данной суммы. Таким образом, имеем
(3).
Теорема доказана.
Следствие
Функция может иметь только один предел при .
Действительно, если и при , то на основании теоремы 1 получим при . Так как предел постоянной функции равен самой функции и единственен, то имеем A-A’=0, то есть A=A’. Замечание
В условии теоремы предполагалось, что каждая из функций имеет предел и доказывалось, что их сумма также имеет предел. Обратное в общем случае неверно, то есть из существования предела суммы не следует существование пределов слагаемых.
Пример
,тогда как не существует и не существует

, то предел произведения при .
существует и равен произведению пределов сомножителей.
Доказательство
Рассмотрим сначала произведение двух сомножителей f(x)g(x) и пусть , .Имеем (4),где ,при . Отсюда получаем (5),где (6).
Из основных теорем о бесконечно малых (теорема 1,2,3) следует, что при .Поэтому на основании равенства (5) будем иметь
(7).
2)Рассмотрим случай произведения трех функций f(x)g(x)h(x), имеющих конечные пределы при . Используя первую часть доказательства находим

Следствие 1
Постоянный множитель можно выносить за знак предела.
Пусть С – постоянная функция,
тогда

, то придел целой положительной степени ее равен такой же степени предела этой функции, то есть

Пример


Лемма
Пусть при . Тогда обратная по величине функция ограничена в некоторой окрестности точки а.
Доказательство
Положим . На основании определения предела функции имеем
,при . Отсюда получаем при
. Таким образом, .
Теорема 3
Если функция f(x) имеет предел при , отличный от нуля, то предел обратной ей по величине функции равен обратной величине предела данной функции, то есть (8).

на бесконечно малую функции, есть бесконечно малая функция, будем иметь
при . Отсюда получаем

Теорема 4
Если делимое f(x) и делитель g(x) имеют пределы при и предел делителя отличен от нуля, то предел их частного при равен частному пределов делимого и делителя, то есть (9).

Доказательство
Пусть . Тогда, используя теорему о пределе произведения (теорема 2) и теорему о пределе обратной величины функции (теорема 3), получим


Пример

и (n – натуральное) существует в точке а и в некоторой ее окрестности , то (10)
Некоторые признаки существования предела функции
Не всякая функция имеет предел, если даже она ограничена. Укажем два признака существования предела функции.
Теорема о промежуточной функции
Пусть в некоторой окрестности точки а функции f(x) заключена между двумя функциями и , имеющими одинаковый предел А при , то есть
(1) и (2), тогда функция f(x) имеет тот же предел, то есть (3).
Доказательство
Из неравенства (1) имеем , отсюда (4). На основании условия (2) для , что и при (5). Поэтому из неравенства (4) получаем при . (6)
Определение
1.Функция f(x) называется возрастающей (не убывающей) на данном множестве Х, если из неравенства следует неравенство (соответственно .

из неравенства следует неравенство (соответственно .
3.Возрастающая или убывающая функция называется монотонной на данном множестве Х.
Теорема
Пусть функция f(x) монотонна и ограничена при xa. Тогда существует соответственно левый предел
и правый предел ее .
Если = , то функция имеет предел в точке а.

дуге)
Теорема Предел отношения синуса бесконечно малой дуги к самой дуге, выраженной в радианах, равен единице, то есть
(1)
Доказательство








Рассмотрим в координатной плоскости круг радиуса R с центром в начале координат


то есть или .
В силу четности функций и это неравенство справедливо и для интервала . Перейдя в этом неравенстве к пределу при и заметив,
что в силу непрерывности функции cosx при х=0 имеет место равенство
получим что равносильно .

где n – натуральное число.
Задаем для n неограниченно возрастающие значения и вычисляем . Получим следующий результат



Как видно из таблицы при увеличении n выражение изменяется все
медленнее и стремится к некоторому пределу, приближенно равному 2,718.
Теорема
Последовательность стремится к конечному пределу, заключенному между 2 и 3.
(Доказательство на основании разложения по биному Ньютона). Этот предел называется числом e. Итак ,е=2,7182818284…

Рассмотрим функцию ,где Можно доказать, что
Другое выражение для числа е. Полагая будем иметь .

; ; . Данные формулы легко получаются из
двух основных формул.
Понятие об асимптотических формулах
Пусть -функции определенные в окрестности точки а. Обобщая
определение о бесконечно малой функции будем говорить, что при (1).
если где при (2).
Если в некоторой окрестности точки а, то из (2) имеем (3).
Определение
Если при справедливо равенство (4), то функция называется асимптотическим выражением для функции f(x) при .
Используется запись при .Если , то при из формулы (4) получаем (5).

Выясним условие существования для функции f(x) ненулевого асимптотического приближения при (6).

(7) где при , то есть при
,причем очевидно также, что при .Их (7) будем иметь (8)
Переходя к пределу при в равенстве (8) и учитывая, что при получим (9).Из формулы (7) (10).
Обратно, если существуют пределы (9),(10), из которых хотя бы один не нулевой, то справедливо асимптотическое разложение (7).
График линейного асимптотического разложения y=kx+b называется асимптотой кривой y=f(x) и имеет вид:








Здесь для точек M(x,y) и M’(x,Y) при

Решение
Используя формулы (9),(10) имеем



Таким образом ~ при .
Непрерывность функции
Приращение аргумента и функции.
Пусть х– некоторое значение данной переменной величины. Наряду с х рассмотрим и другое значение этой переменной величины .
Определение 1
Приращением некоторой переменной величины называется разность между новым значением этой величины и ее прежним значением. В нашем случае

х.
Прибавляя к значению переменной величины ее приращение, получаем приращенное значение этой величины.
-приращенное значение величины х.
Рассмотрим функцию y=f(x) (1)
Даём для х, тогда y получает соответствующее приращение . Очевидно это можно записать (2). Из (1) и (2) следует (3).
Геометрическая интерпретация








Кривая АВ – график функции f(x).

.Тогда ордината y получит приращение . Точка M(x,y) займет положение .
Пусть С – точка пересечения прямой параллельной ОХ и перпендикуляра M’N’ на ОХ.
Очевидно .
Может случиться, что для некоторого х при стремлении точка M’ неограниченно приблизится к М, то есть .
В таком случае y=f(x) называется непрерывной при данном значении х.
Определение 2
Функция называется непрерывной в данной точке, если в этой точке бесконечно
малому приращению аргумента соответствует бесконечно малое приращение функции.
Используя понятие предела функции, получаем развернутое определение
непрерывности функции в точке.
Определение 3
Функция f(x) непрерывна в точке тогда и только тогда, когда , такое, что (4),если и , любое допустимое приращение.

на этом множестве, то есть
2) непрерывна в каждой точке этого множества, то есть справедливо равенство
(5), где .
Пример
Исследовать на непрерывность функцию
Решение
Давая х приращение , получим
Очевидно, каково бы ни было фиксированное значение х, если ,то ,то есть функция непрерывна при любом
Определение 5
Точка, в которой нарушается непрерывность функции называется точкой разрыва этой функции. Если -точка разрыва функции y=f(x), то возможны два случая:
1) функция f(x) определена при ,причём при

и говорить о приращении функции в точке
не имеет смысла . В этом случае условимся называть точкой разрыва функции f(x) только тогда, когда функция f(x) определена в непосредственной близости значения .
Если можно изменить или дополнительно определить функцию f(x) в точке
,то есть выбрать число , так, что измененная или дополненная функция f(x) будет непрерывна при ,то эта точка называется устранимой точкой разрыва функции f(x).
В противном случае, то есть когда функция f(x) остается разрывной при при любом выборе числа значение называется неустранимой точкой разрыва функции f(x).
Пример 1
Рассмотрим функцию Е(х), равную целой части числа х, то есть, если x=n+q, где n – целое число, , то E(x)=n

x=1 и достаточно малом получаем



Отсюда, приняв во внимание, что E(1)=1 получим

не стремится к нулю при
то есть функция разрывная при х=1. Аналогичное рассуждение можно провести и для x=k, где k -целое.
Пример 2
Функция , не определена при х=2, но имеет смысл для всех значений







Какое бы значение не приписывали числу f(2), всегда будем иметь
при . Таким образом, при х=2 при любом выборе значения f(2) при , следовательно, эта функция имеет неустранимую точку разрыва при х=2.

в точке, эквивалентное, приведенному выше.
Определение 6
Функция f(x) называется непрерывной при , если
эта функция определена при ;
имеет место равенство (1).
То есть функция непрерывна в данной точке , тогда и только тогда, когда предел функции при равен значению функции в предельной точке. Точка - предельная точка области определения функции f(x).
Для функции, непрерывной на множестве Х, в силу формулы (1) для каждого значения
выполнено неравенство
Так как ,то отсюда получаем (2) , то есть , если функция непрерывна, то знаки предела и функции перестановочны.
Справедливо усиленное свойство перестановочности функции f(x) и предела, а именно
- непрерывная функция при , тогда для f(x) имеем

функция непрерывная.
Доказательство
Пусть - непрерывные функции на множестве Х и , тогда
, то есть предел суммы
при равен значению этой суммы при . Следовательно также непрерывная на множестве Х.
Теорема 2
Произведение конечного числа непрерывных функций есть функция непрерывная.
Доказательство аналогично доказательству в теореме 1.
Следствие
Полином - непрерывная функция.
Теорема 3
Частное от деления двух непрерывных функций есть функция непрерывная во всех точках, в которых делитель отличен от 0.
Доказательство аналогичное.

непрерывна всюду за исключением тех значений х, где знаменатель обращается в 0.
Теорема 4
Непрерывная функция от непрерывной функции также непрерывна. Сложная функция, состоящая из непрерывных функций, непрерывна.
Доказательство
Пусть и - определена в этой точке, причем непрерывная в точке
, а f(u) непрерывная в точке . На основании усиленного свойства перестановочности функции и предела имеем , то есть непрерывная в точке .
Пример
Функции и - непрерывные в силу непрерывности функций sinx и
Теорема 5
Если функция y=f(x) непрерывная и строго монотонная на интервале (a,b), то существует однозначная обратная функция , определенная на интервале (f(a),f(b)), которая также непрерывная и монотонная.

некоторого значения , при котором функция f(x) теряет смысл, то есть становиться неопределенной. Каким образом можно выбрать число . Чтобы дополненная функция была непрерывной при . Для этого необходимо и достаточно выполнение равенства . Операция нахождения предела функции f(x) при в этом случае называется раскрытием неопределенности, а сам предел, если он существует носит название истинного значения функции f(x) при
Пример
при х=2 функция не определена. Полагая, дополнительно

получим функцию непрерывную всюду, в том числе и при х=2. Если же положить ,то то соответствующая функция будет разрывная при х=2.

точкой разрыва первого рода, если существуют конечные односторонние пределы функции


При этом f(x) не обязательно должна быть определена в точке , то есть может не существовать





- называется скачком функции f(x) в точке
Все прочие точки разрыва функции f(x) называются ее точками разрыва второго рода.
Точки бесконечного разрыва характеризуются тем, что для них существуют односторонние пределы

называется вертикальной асимптотой графика функции f(x)