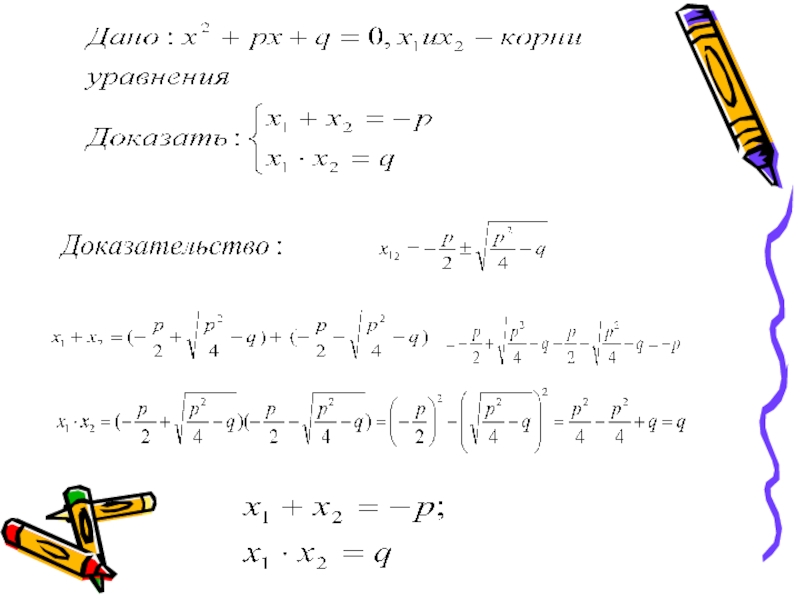- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Теорема Виета презентация
Содержание
- 1. Теорема Виета
- 2. ПЛАН УРОКА Проверка домашней работы Математический диктант
- 3. Проверка домашней работы №264(2,3)
- 4. Математический диктант 1.Уравнение какого вида называется полным
- 5. Зависимость между коэффициентами и корнями уравнения
- 6. Франсуа Виет (1540-1603) Французский математик
- 8. Применение теоремы Виета Найти сумму и произведение
- 9. Теорема обратная к теореме Виета Если сумма
- 10. Теорема обратная помогает решать приведенное квадратное уравнение,не
- 11. Найдите корни уравнения с помощью теоремы обратной
- 12. Домашняя работа: Параграф 8, №148(1,2,3)
- 13. Понял я сейчас , друзья! Теорему свою,я
Слайд 1Теорема Виета
Цель:
Изучить теорему Виета.
Обратную к ней теорему
Научиться применять их
При
Слайд 2ПЛАН УРОКА
Проверка домашней работы
Математический диктант
Изучение новой темы
Работа в группах
Домашнее задание
Слайд 3Проверка домашней работы
№264(2,3)
18-(х-5)(х-4)=-2
18-(х2 - 4х -5х +20) = - 2
18 - х2 + 9х – 20 + 2=0
- х2 + 9х =0 I. Х=0 или II. –х+9=0
х=9
Ответ: 0; 9
3). (3х – 1)2 =1
9х2 -6х +1 – 1 =0 9х2 – 6х =0 3х(3х -2 )=0
3х=0 или 3х-2=0
Х=0 х=2/3
Ответ: 0; 2/3
№ 270
ах2 – 3х – 5= 0, если х1=1
а∙1 - 3∙1 – 5 =0
а – 8 = 0 а=8
Ответ: при а=8
№ 275
х2 – 7х + k = 0, если х=- 2
( -2)2 – 7(-2) +k = 0
4 + 14 + k =0
k =- 18
Ответ: при k = - 18
Слайд 4Математический диктант
1.Уравнение какого вида называется полным квадратным уравнением?
2.Уравнение какого вида называется
3.В каком случае квадратное уравнение имеет два одинаковых корня?
4.Два различных корня?
5.Не имеет корней?
6.Записать формулу корней квадратного уравнения общего вида.
7.Записать формулу корней приведенного квадратного уравнения
8.Записать формулу корней квадратного уравнения со вторым четным коэффициентом.
1. ах2 +вх + с = 0, а≠0
2. х2 +px + q = 0
3. D=0
4. D>0
5. D<0
6.
7.
Слайд 5Зависимость между коэффициентами и корнями уравнения
Уравнения
I. х2 – 2х – 3
II х2 + 5х – 6 = 0
III. Х2 - х – 12 = 0
IV Х2 + 7х + 12 = 0
V. Х2 - 8х + 15 = 0
p q Корни х1и х1 х1+х2 х1х 2
-2 -3 3 и -1 2 -3
5 -6 -6 и 1 -5 -6
-1 -12 4 и -3 1 -12
7 12 -3 и -4 -7 12
-8 15 3 и 5 8 15
Слайд 8Применение теоремы Виета
Найти сумму и произведение корней № 147
Составьте квадратное
I. а) 3 и 5 б) - 6 и -3
А) х2 – 8х +15=0 б) х2+ 9х + 18=0
II а) -3 и -4 б) -1 и -2
а) х2 +7х + 12=0 б) х2 + 3х + 2=0
III а) 3 и -1 б) 7и -3
а) х2 -2х -3=0 б) х2 – 4х -21 =0
IV а) -6 и 1 б) 3 и -1
а) х2 + 5х -6 =0 б) х2 -2х -3 =0
V а) 1 и -5 б) 7 и -6
а) х2 + 4х -5 =0 б) х2 –х -42 =0
Слайд 9Теорема обратная к теореме Виета
Если сумма двух чисел равна - p,
Пусть некоторые числа m и n таковы, что их сумма равна –p , а произведение равно q .
Покажем, что они являются корнями данного уравнения.
Если m+n=-p, mn=q, то уравнение х2 +px + q = 0 можно записать
Х2 – (m+n)х +mn =0.
Подставив вместо х число m, получим:
m2 – (m+n)m +mn = m2- m2- mn + mn = 0 .
Значит m - корень уравнения х2 +px + q = 0.
Если теперь вместо х подставить n, то получим:
n2 – (m+n)n + mn = n2 –mn – n2 +mn = 0,
значит n - корень уравнения х2 +px + q = 0.
Слайд 10Теорема обратная помогает решать приведенное квадратное уравнение,не пользуясь формулами корней квадратного
Решим уравнение х2 +2x - 15 = 0, применяя обратную теорему.
Х1 + х2 = -2
х1∙ х2 =-15
такими числами могут быть только 3 и -5.
Действительно 3+ (-5) = -2
3∙(-5) = -15
Итак: х1= 3
х2=-5
Слайд 11Найдите корни уравнения с помощью теоремы обратной теореме Виета
I. Х2+17х-18=0
II х2-17х-18=0
х2-15х+36=0
III х2-11х+18=0
х2+20х+36=0
IV х2+7х-18=0
х2+37х+36=0
V х2+9х+18=0
х2+9х-36=0
I -18 и 1
9 и 4
II. 17 и -1
12 и 3
III. 2 и 9
-18 и -2
IV. -9 и 2
-36 и – 1
V. -6 и -3
-12 и 3
Слайд 13Понял я сейчас , друзья! Теорему свою,я придумал не зря Юный друг,ты сегодня
Благодарю за урок