- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Теория графов. Его величество граф презентация
Содержание
- 1. Теория графов. Его величество граф
- 2. Введение С дворянским титулом «граф» тему моей
- 3. Что такое граф Слово «граф» в математике
- 4. Что такое граф В математике определение графа
- 5. Что такое граф Количество рёбер, выходящих из
- 6. История возникновения графов Термин "граф" впервые появился
- 7. История возникновения графов Основы теории графов как
- 8. Задача о Кенигсбергских мостах Бывший Кенигсберг (ныне
- 9. Задача о Кенигсбергских мостах Кенигсбергцы предлагали приезжим
- 10. дальше Я здесь уже был!
- 11. Задача о Кенигсбергских мостах Пройти по Кенигсбергским
- 12. Задача о Кенигсбергских мостах Но, поскольку граф
- 13. Одним росчерком Граф, который можно нарисовать, не
- 14. Одним росчерком Если все вершины графа четные,
- 15. Одним росчерком Граф, имеющий всего две нечетные
- 16. Одним росчерком Граф, имеющий более двух нечетных
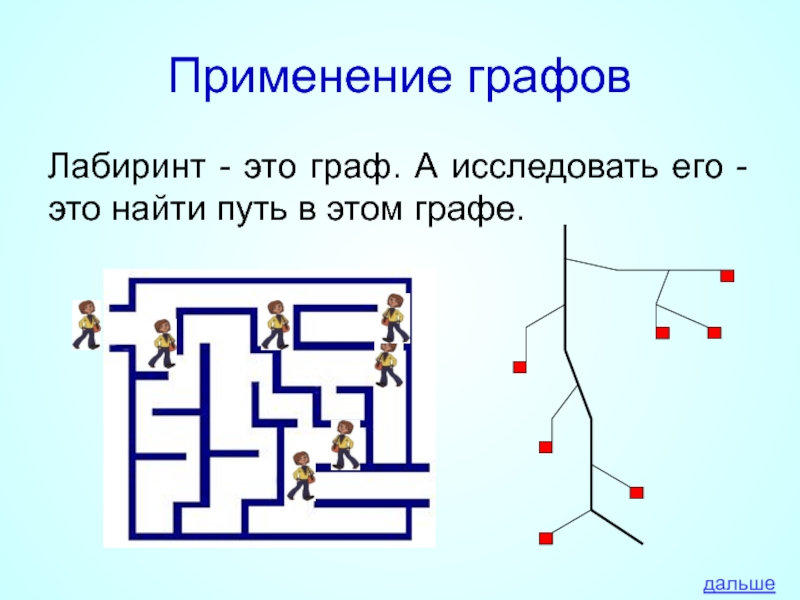
- 18. Применение графов Лабиринт - это граф. А
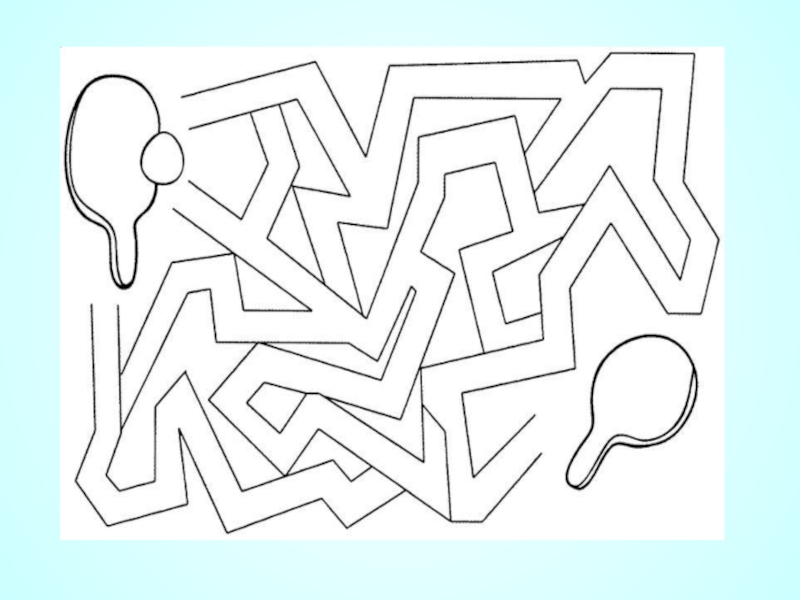
- 20. Первый многосвязный садовый лабиринт был сооружён в 1820-е годы в Чевнинге в Великобритании.
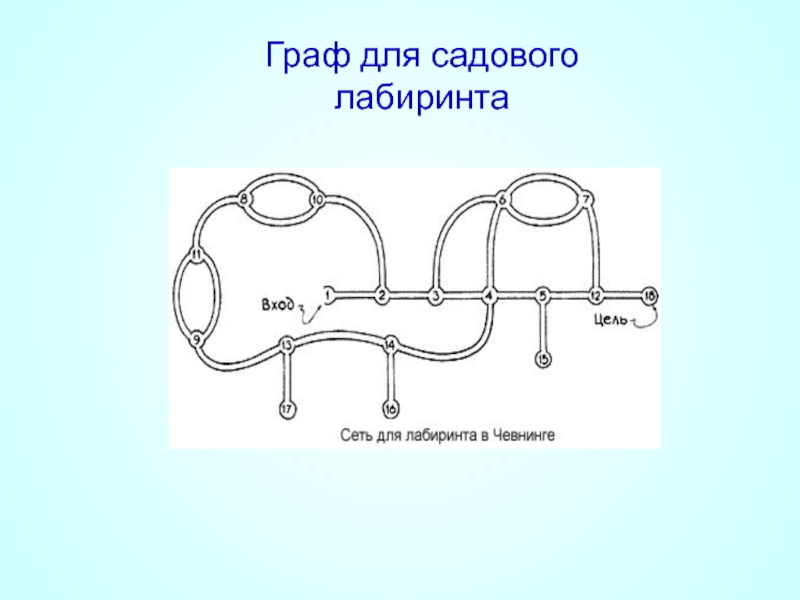
- 21. Граф для садового лабиринта
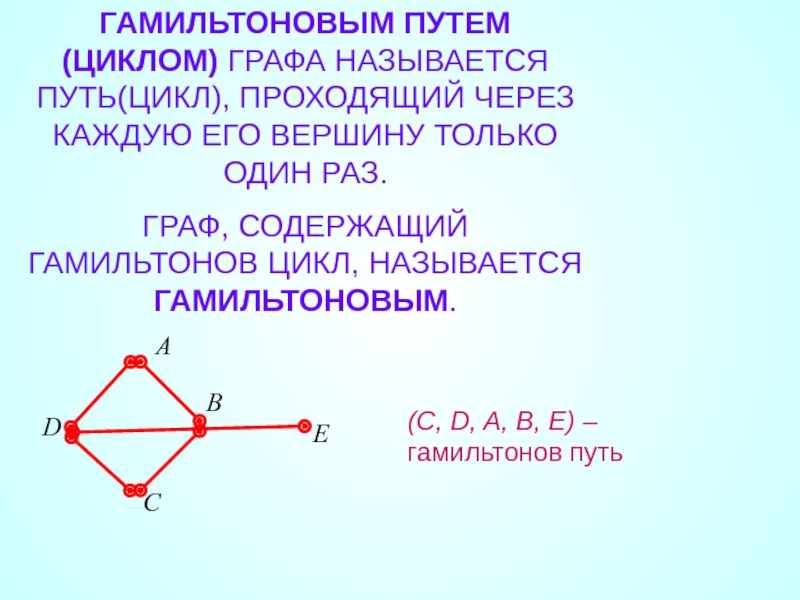
- 22. ГАМИЛЬТОНОВЫМ ПУТЕМ(ЦИКЛОМ) ГРАФА НАЗЫВАЕТСЯ ПУТЬ(ЦИКЛ), ПРОХОДЯЩИЙ ЧЕРЕЗ
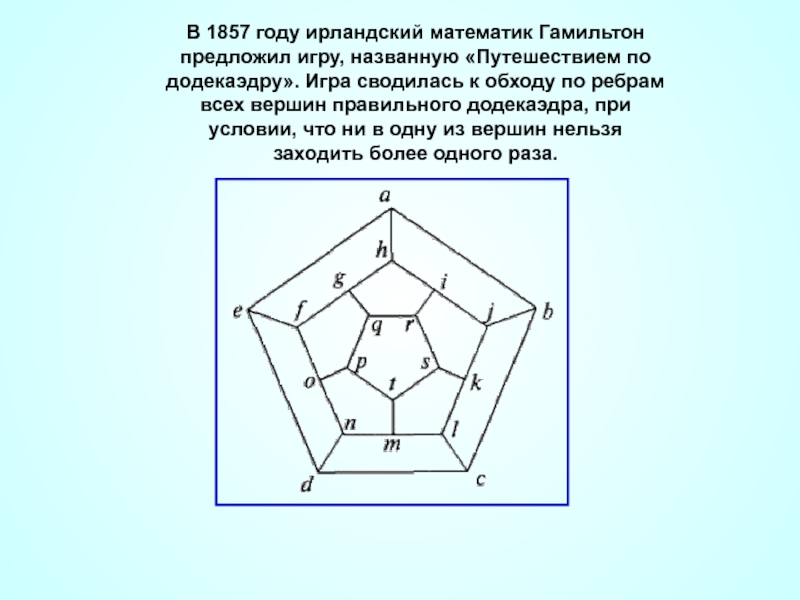
- 23. В 1857 году ирландский математик Гамильтон предложил
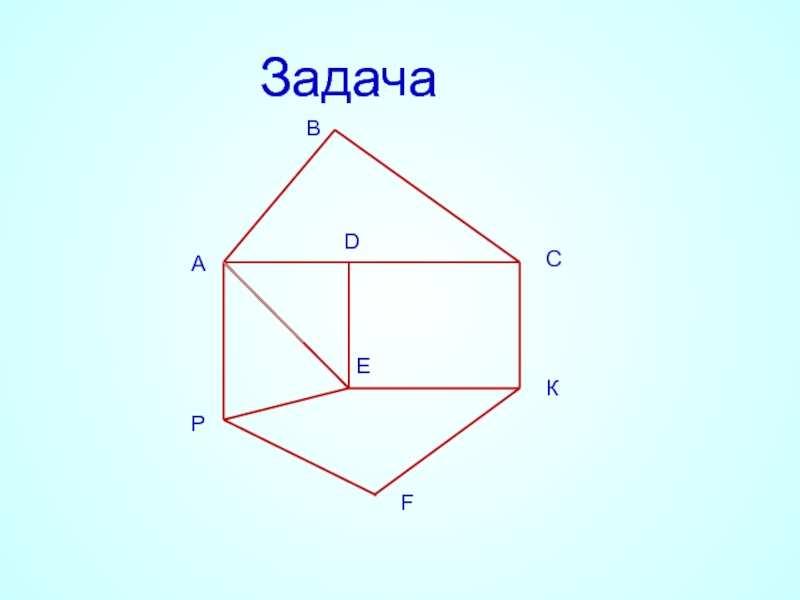
- 24. Задача А В С К Е D P F
- 25. Выводы Графы – это замечательные математические объекты,
- 26. ТЕОРЕМА В ГРАФЕ СУММА СТЕПЕНЕЙ ВСЕХ
- 27. ГРАФ НАЗЫВАЕТСЯ ПОЛНЫМ, ЕСЛИ ЛЮБЫЕ ДВЕ ЕГО
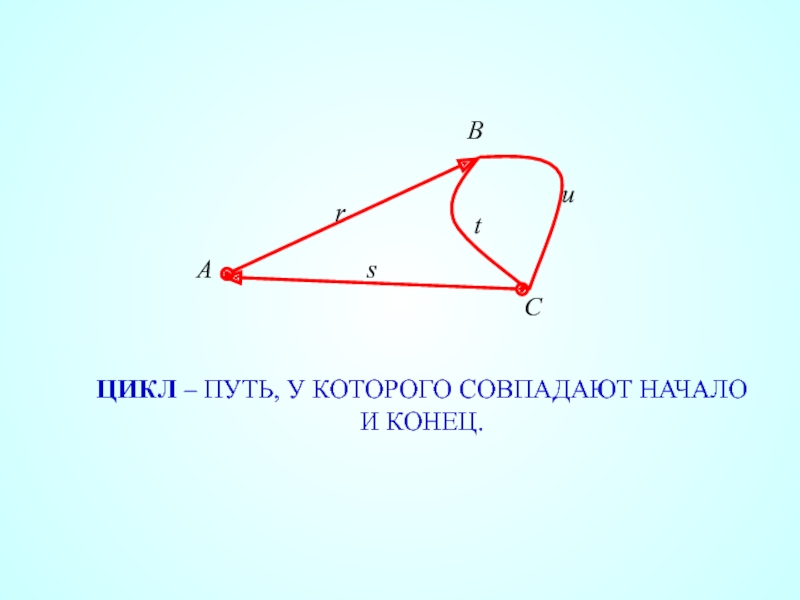
- 28. ЦИКЛ – ПУТЬ, У КОТОРОГО СОВПАДАЮТ НАЧАЛО И КОНЕЦ.
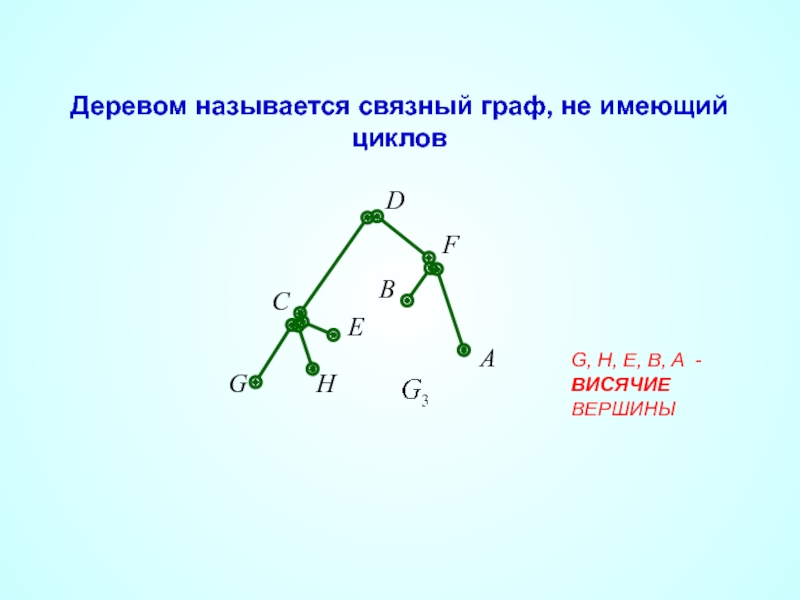
- 29. G, H, E, B, A - ВИСЯЧИЕ ВЕРШИНЫ Деревом называется связный граф, не имеющий циклов
- 30. Применение графов Использует графы и дворянство. На
- 31. Перечислить все возможные варианты обедов из трех
- 32. Задача №2. У Аси есть любимый костюм,
- 33. Применение графов Задача: Аркадий, Борис. Владимир, Григорий
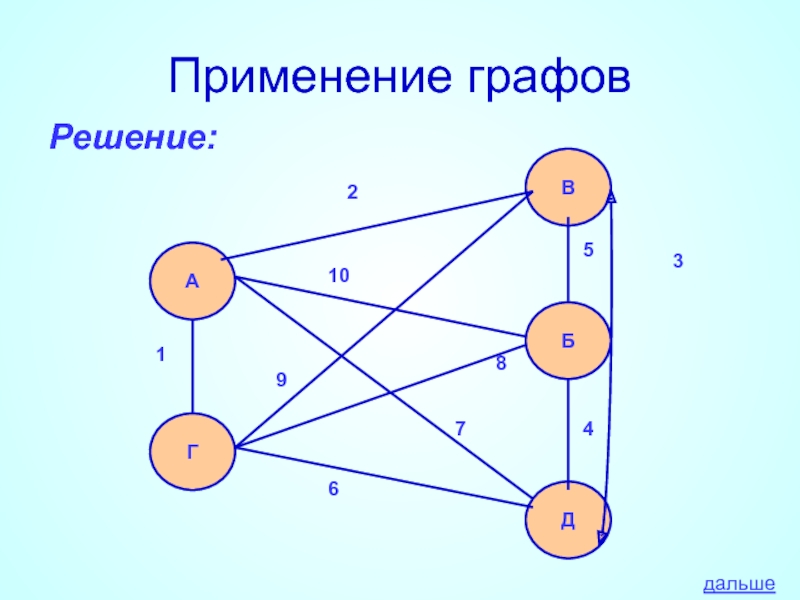
- 34. Применение графов Решение: А Г В Б
- 35. Задача 2. По окончании деловой встречи специалисты
- 36. Логические задачи
- 37. Известно, что в настоящий момент:
- 44. В одном дворе живут четыре друга.
- 45. Вадим Коля Сергей Андрей слесарь токарь электрик
- 46. Андрей, Борис, Володя, Даша, Галя договорились созвониться
- 47. Спасибо за внимание
Слайд 2Введение
С дворянским титулом «граф» тему моей работы связывает только общее происхождение
Г
Р
А
Ф
И
О
дальше
Слайд 3Что такое граф
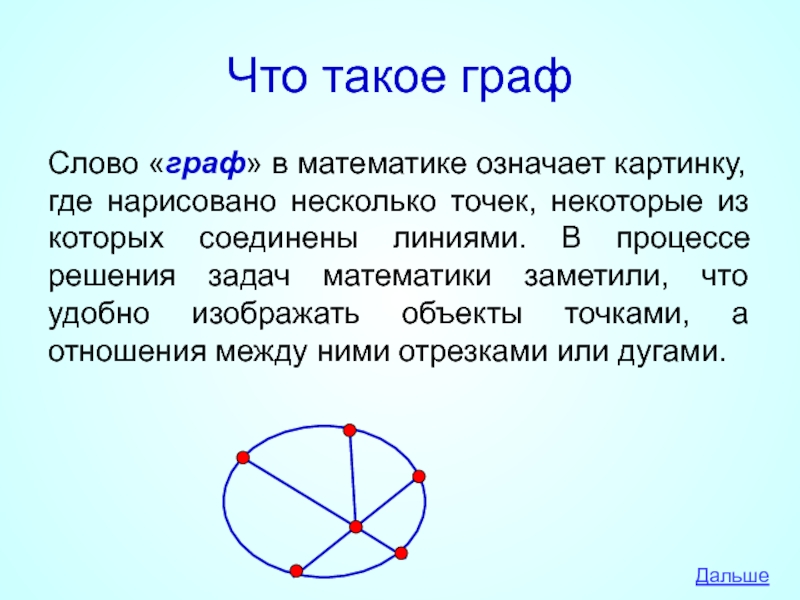
Слово «граф» в математике означает картинку, где нарисовано несколько
Дальше
Слайд 4Что такое граф
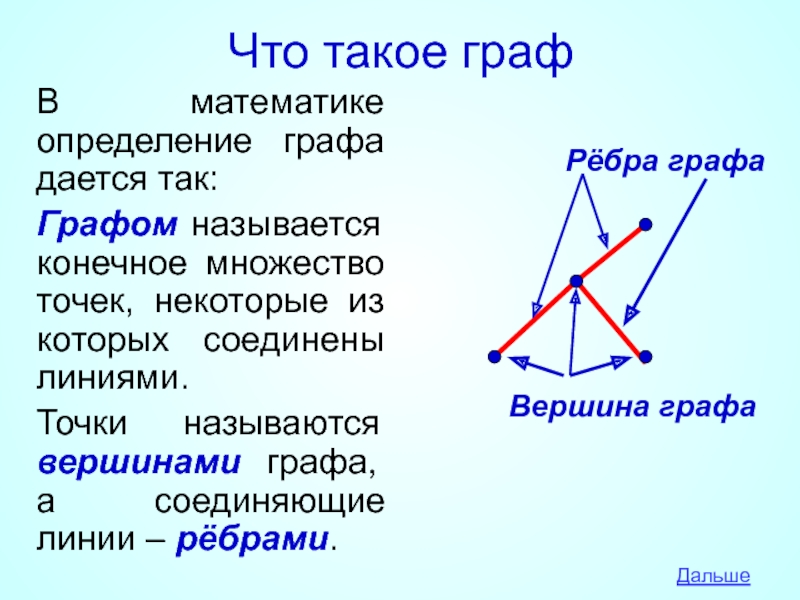
В математике определение графа дается так:
Графом называется конечное множество
Точки называются вершинами графа, а соединяющие линии – рёбрами.
Рёбра графа
Вершина графа
Дальше
Слайд 5Что такое граф
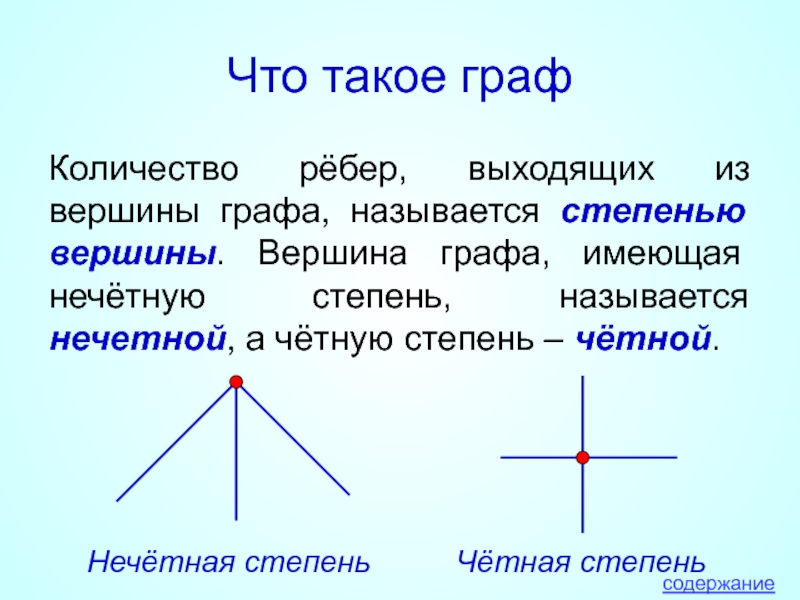
Количество рёбер, выходящих из вершины графа, называется степенью вершины.
Нечётная степень
Чётная степень
содержание
Слайд 6История возникновения графов
Термин "граф" впервые появился в книге венгерского математика Д.
Дальше
Слайд 7История возникновения графов
Основы теории графов как математической науки заложил в 1736
содержание
Слайд 8Задача о Кенигсбергских мостах
Бывший Кенигсберг (ныне Калининград) расположен на реке Прегель.
Дальше
Слайд 9Задача о Кенигсбергских мостах
Кенигсбергцы предлагали приезжим следующую задачу: пройти по всем
Дальше
Слайд 11Задача о Кенигсбергских мостах
Пройти по Кенигсбергским мостам, соблюдая заданные условия, нельзя.
дальше
Слайд 12Задача о Кенигсбергских мостах
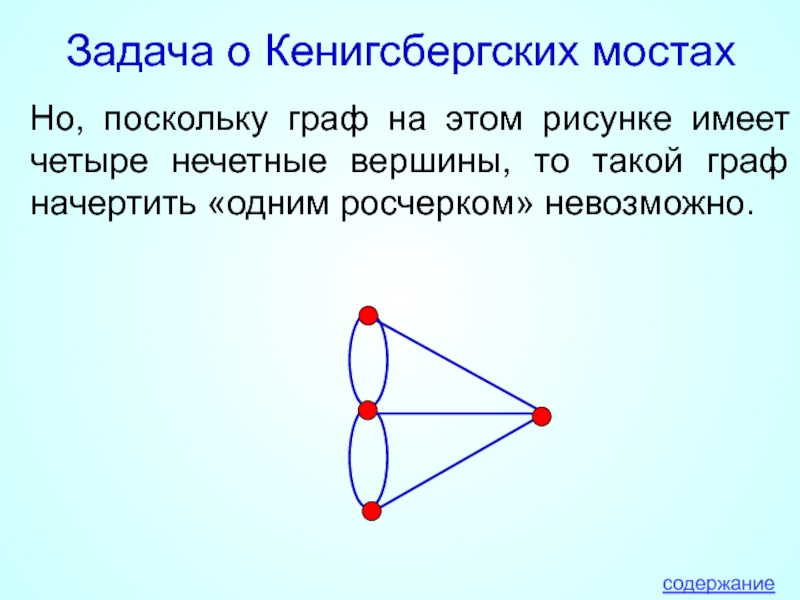
Но, поскольку граф на этом рисунке имеет четыре
содержание
Слайд 13Одним росчерком
Граф, который можно нарисовать, не отрывая карандаша от бумаги, называется
Решая задачу О кенигсбергских мостах, Эйлер сформулировал свойства графа:
Невозможно начертить граф с нечетным числом нечетных вершин.
дальше
Слайд 14Одним росчерком
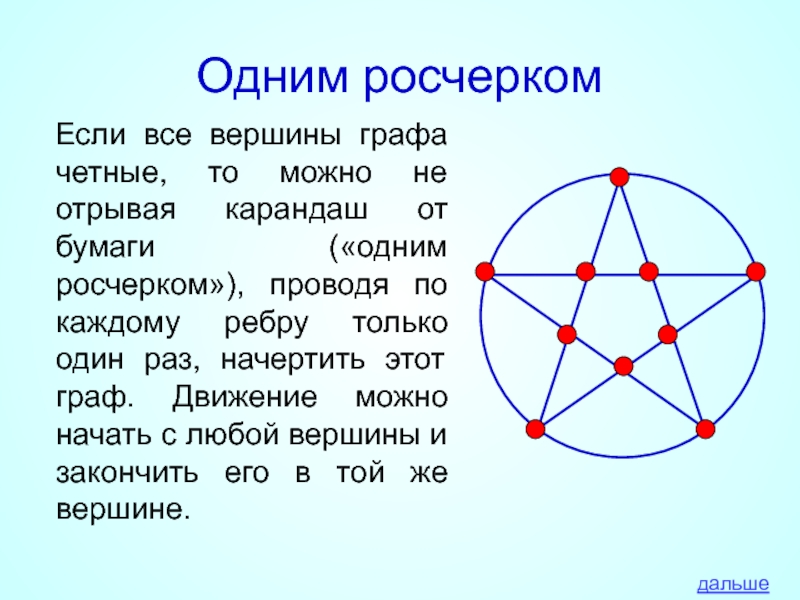
Если все вершины графа четные, то можно не отрывая карандаш
дальше
Слайд 15Одним росчерком
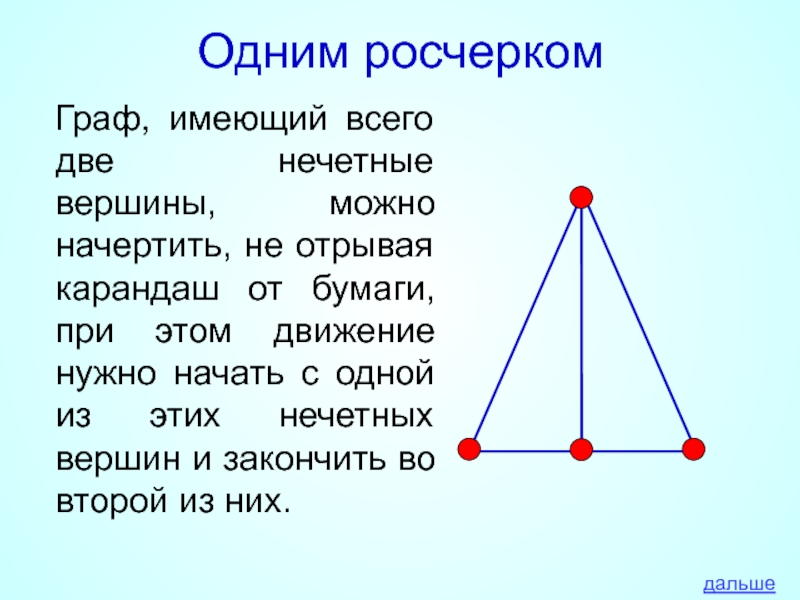
Граф, имеющий всего две нечетные вершины, можно начертить, не отрывая
дальше
Слайд 16Одним росчерком
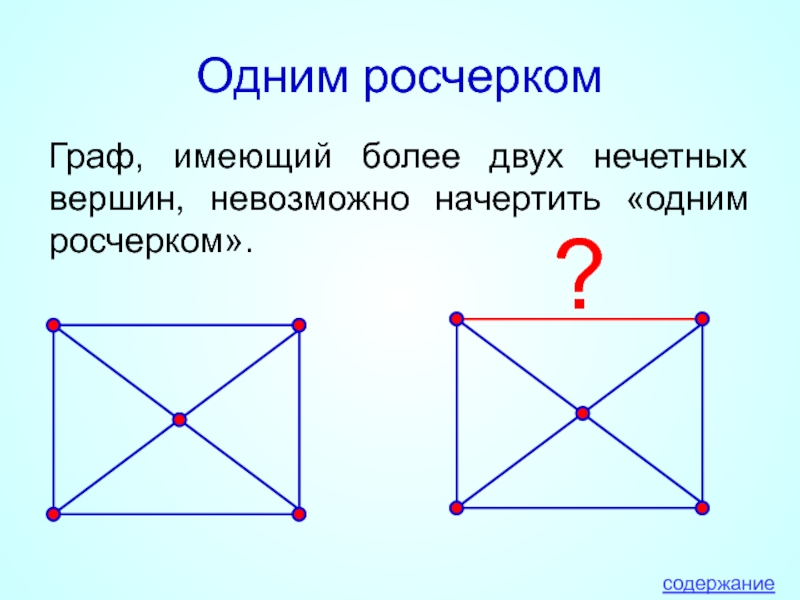
Граф, имеющий более двух нечетных вершин, невозможно начертить «одним росчерком».
?
содержание
Слайд 18Применение графов
Лабиринт - это граф. А исследовать его - это найти
дальше
Слайд 20Первый многосвязный садовый лабиринт был сооружён в 1820-е годы в Чевнинге
Слайд 22ГАМИЛЬТОНОВЫМ ПУТЕМ(ЦИКЛОМ) ГРАФА НАЗЫВАЕТСЯ ПУТЬ(ЦИКЛ), ПРОХОДЯЩИЙ ЧЕРЕЗ КАЖДУЮ ЕГО ВЕРШИНУ ТОЛЬКО
ГРАФ, СОДЕРЖАЩИЙ ГАМИЛЬТОНОВ ЦИКЛ, НАЗЫВАЕТСЯ ГАМИЛЬТОНОВЫМ.
A
B
C
D
E
(C, D, A, B, E) – гамильтонов путь
Слайд 23В 1857 году ирландский математик Гамильтон предложил игру, названную «Путешествием по
Слайд 25Выводы
Графы – это замечательные математические объекты, с помощью, которых можно решать
В математике даже есть специальный раздел, который так и называется: «Теория графов».
содержание
Слайд 26ТЕОРЕМА
В ГРАФЕ СУММА СТЕПЕНЕЙ ВСЕХ ЕГО ВЕРШИН – ЧИСЛО ЧЕТНОЕ,
ТЕОРЕМА
ЧИСЛО НЕЧЕТНЫХ ВЕРШИН ЛЮБОГО ГРАФА – ЧЕТНО.
СЛЕДСТВИЕ
ЧИСЛО ВЕРШИН МНОГОГРАННИКА, В КОТОРЫХ СХОДИТСЯ НЕЧЁТНОЕ ЧИСЛО РЁБЕР, ЧЁТНО.
Степень А +степень В + степень С +…= 2*число рёбер
НЕЧЁТНОЕ ЧИСЛО ЗНАКОМЫХ В ЛЮБОЙ КОМПАНИИ ВСЕГДА ЧЁТНО.
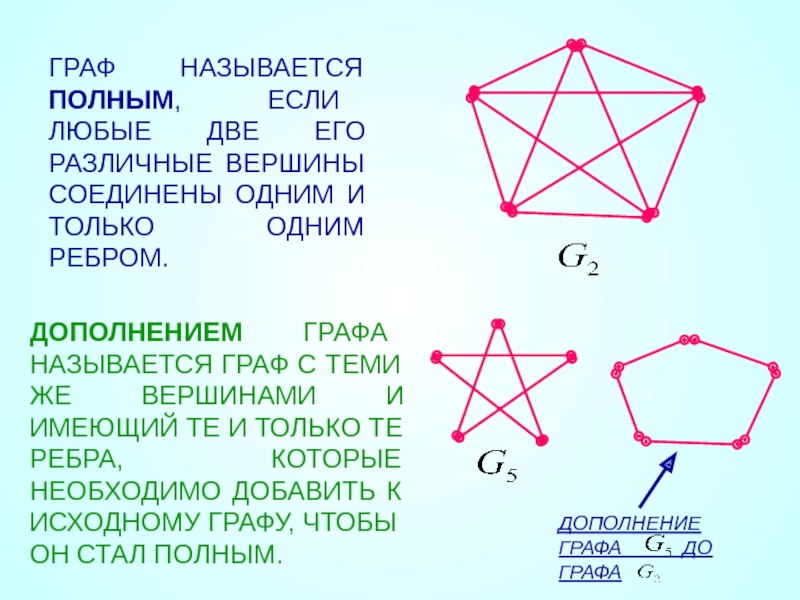
Слайд 27ГРАФ НАЗЫВАЕТСЯ ПОЛНЫМ, ЕСЛИ ЛЮБЫЕ ДВЕ ЕГО РАЗЛИЧНЫЕ ВЕРШИНЫ СОЕДИНЕНЫ ОДНИМ
ДОПОЛНЕНИЕМ ГРАФА НАЗЫВАЕТСЯ ГРАФ С ТЕМИ ЖЕ ВЕРШИНАМИ И ИМЕЮЩИЙ ТЕ И ТОЛЬКО ТЕ РЕБРА, КОТОРЫЕ НЕОБХОДИМО ДОБАВИТЬ К ИСХОДНОМУ ГРАФУ, ЧТОБЫ ОН СТАЛ ПОЛНЫМ.
ДОПОЛНЕНИЕ ГРАФА ДО ГРАФА
Слайд 30Применение графов
Использует графы и дворянство.
На рисунке приведена часть генеалогического дерева знаменитого
дальше
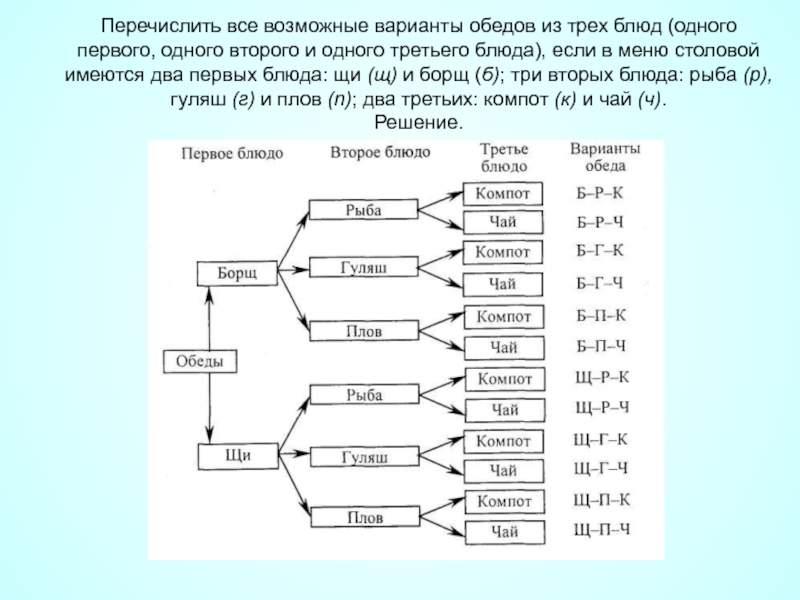
Слайд 31Перечислить все возможные варианты обедов из трех блюд (одного первого, одного
Решение.
Слайд 32Задача №2. У Аси есть любимый костюм, в котором она ходит
а) Нарисуйте дерево возможных вариантов Асиной одежды.
Задача №3. Группа туристов планирует осуществить поход по маршруту Антоново – Борисово – Власово – Грибово. Из Антонова в Борисово можно сплавиться по реке или дойти пешком. Из Борисова во Власово можно дойти пешком или доехать на велосипедах. Из Власова в Грибово можно доплыть по реке, доехать на велосипедах или дойти пешком.
а) Нарисуйте дерево возможных вариантов похода.
б) Сколько всего вариантов похода могут выбрать туристы?
в) Сколько есть полностью не пеших вариантов?
Слайд 33Применение графов
Задача:
Аркадий, Борис. Владимир, Григорий и Дмитрий при встрече обменялись рукопожатиями
дальше
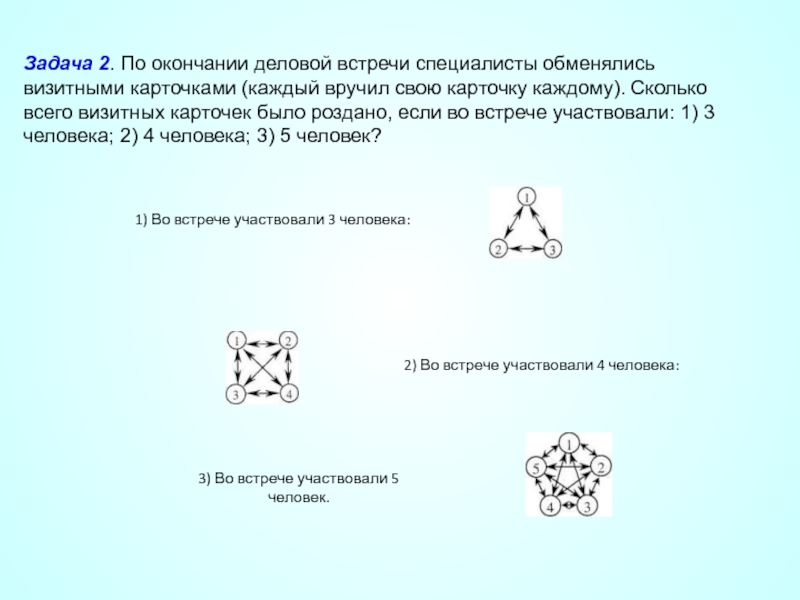
Слайд 35Задача 2. По окончании деловой встречи специалисты обменялись визитными карточками (каждый
1) Во встрече участвовали 3 человека:
2) Во встрече участвовали 4 человека:
3) Во встрече участвовали 5 человек.
Слайд 37 Известно, что в настоящий момент:
Ваня сыграл шесть партий;
Толя сыграл
Леша и Дима сыграли по три партии;
Семен и Илья сыграли по две партии;
Женя сыграл одну партию.
Условие задачи
Требуется определить:
с кем сыграл Леша.
Шахматный турнир проводится по круговой системе, при которой каждый участник встречается с каждым ровно один раз, участвуют семь школьников.
Слайд 38
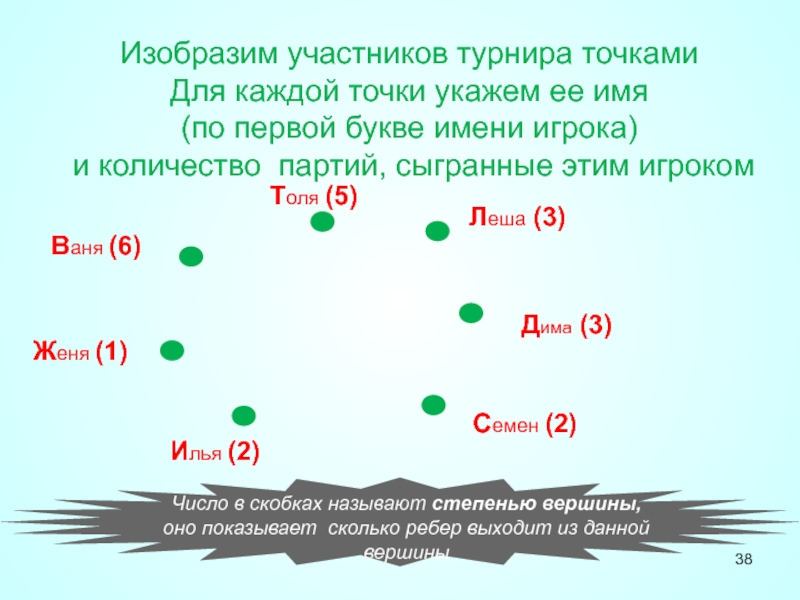
Число в скобках называют степенью вершины, оно показывает сколько ребер выходит
Ваня (6)
Толя (5)
Леша (3)
Дима (3)
Семен (2)
Илья (2)
Женя (1)
Изобразим участников турнира точками
Для каждой точки укажем ее имя
(по первой букве имени игрока)
и количество партий, сыгранные этим игроком
Слайд 39
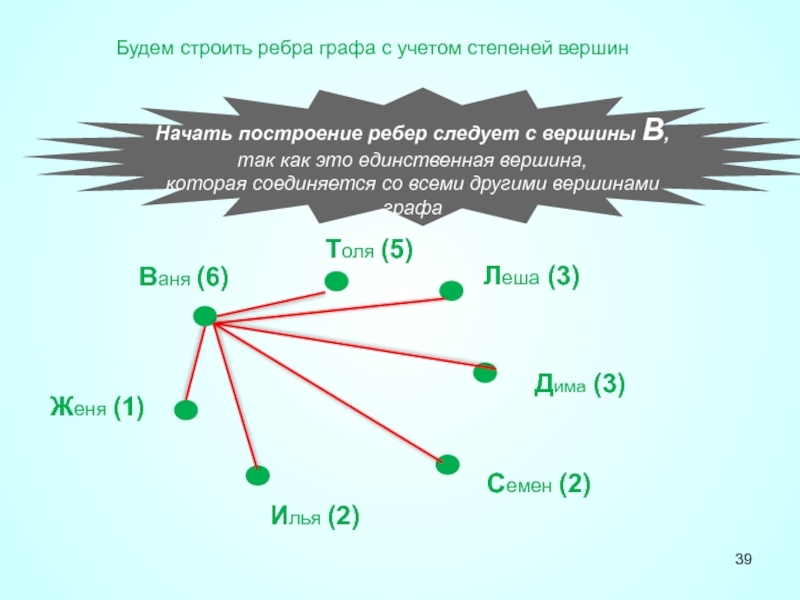
Начать построение ребер следует с вершины В, так как это единственная
которая соединяется со всеми другими вершинами графа
Ваня (6)
Толя (5)
Леша (3)
Дима (3)
Семен (2)
Илья (2)
Женя (1)
Будем строить ребра графа с учетом степеней вершин
Слайд 40
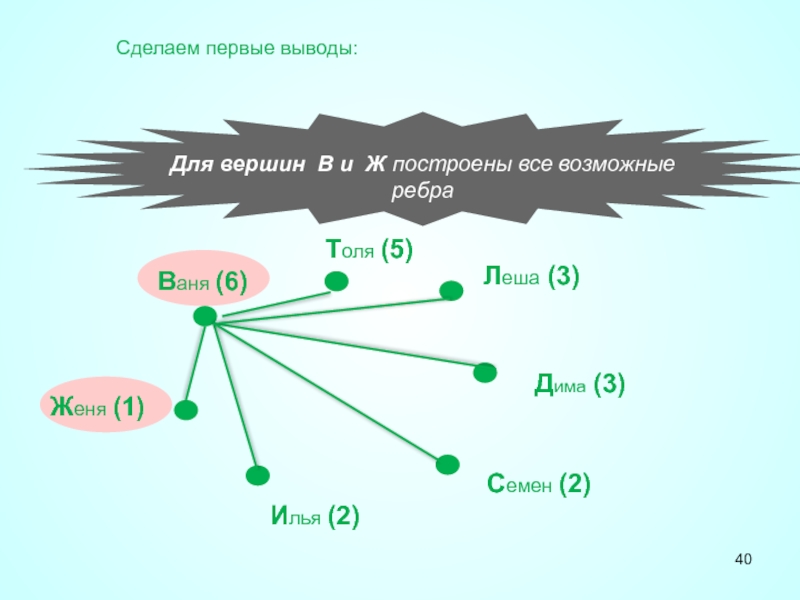
Для вершин В и Ж построены все возможные ребра
Ваня (6)
Толя (5)
Леша
Дима (3)
Семен (2)
Илья (2)
Женя (1)
Сделаем первые выводы:
Слайд 41
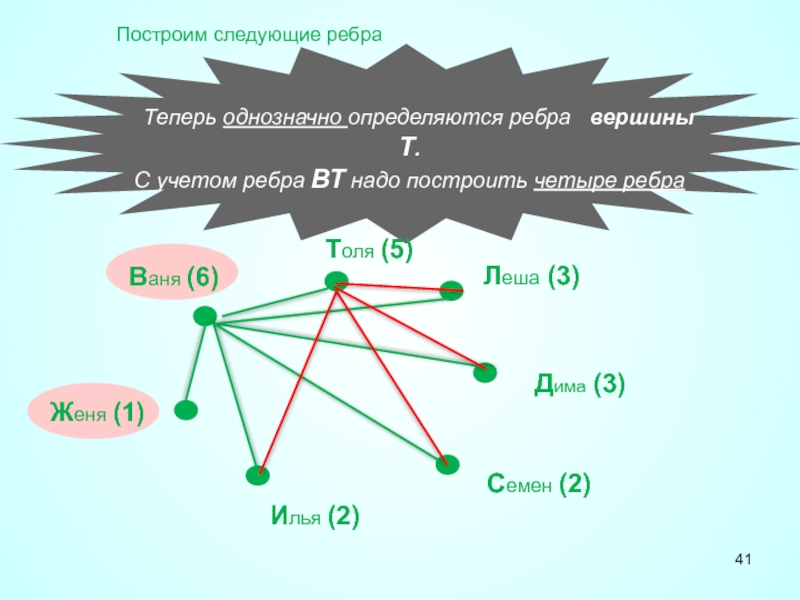
Теперь однозначно определяются ребра вершины Т.
С учетом ребра ВТ надо
Ваня (6)
Толя (5)
Леша (3)
Дима (3)
Семен (2)
Илья (2)
Женя (1)
Построим следующие ребра
Слайд 42
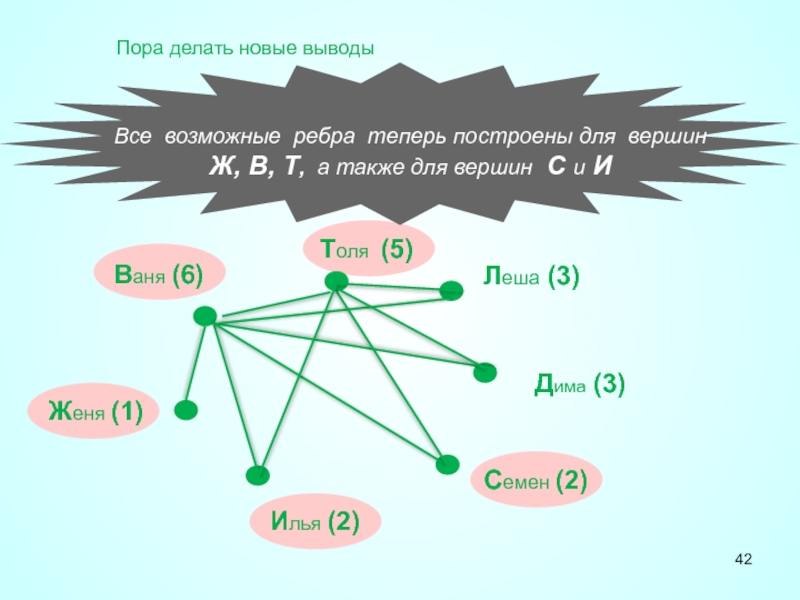
Все возможные ребра теперь построены для вершин Ж, В,
Ваня (6)
Толя (5)
Леша (3)
Дима (3)
Семен (2)
Илья (2)
Женя (1)
Пора делать новые выводы
Слайд 43
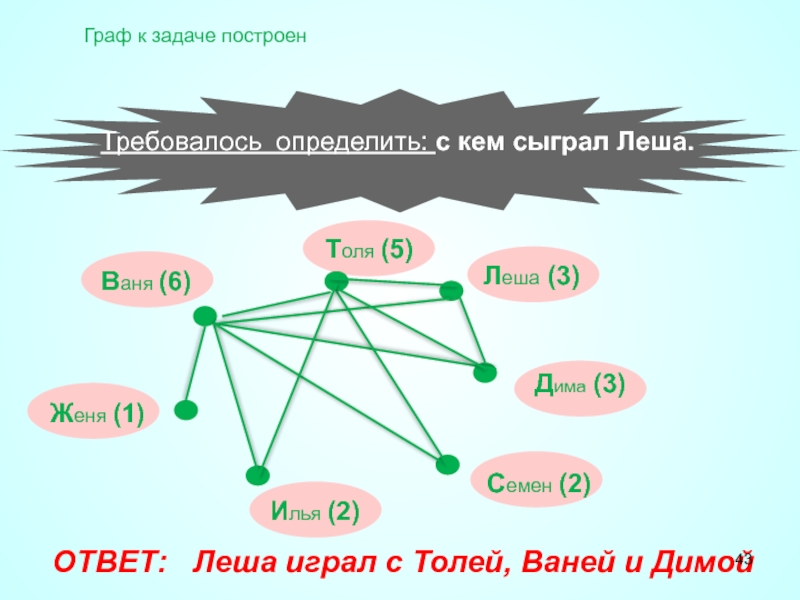
ОТВЕТ: Леша играл с Толей, Ваней и Димой
Ваня (6)
Толя (5)
Леша
Дима (3)
Семен (2)
Илья (2)
Женя (1)
Требовалось определить: с кем сыграл Леша.
Граф к задаче построен
Слайд 44В одном дворе живут четыре друга.
Вадим и шофер старше Сергея,
Николай
Электрик-младший из друзей.
По вечерам Андрей и токарь играют в домино против Сергея и электрика.
Определите профессию каждого из друзей.
Условие задачи
Слайд 45Вадим
Коля
Сергей
Андрей
слесарь
токарь
электрик
шофер
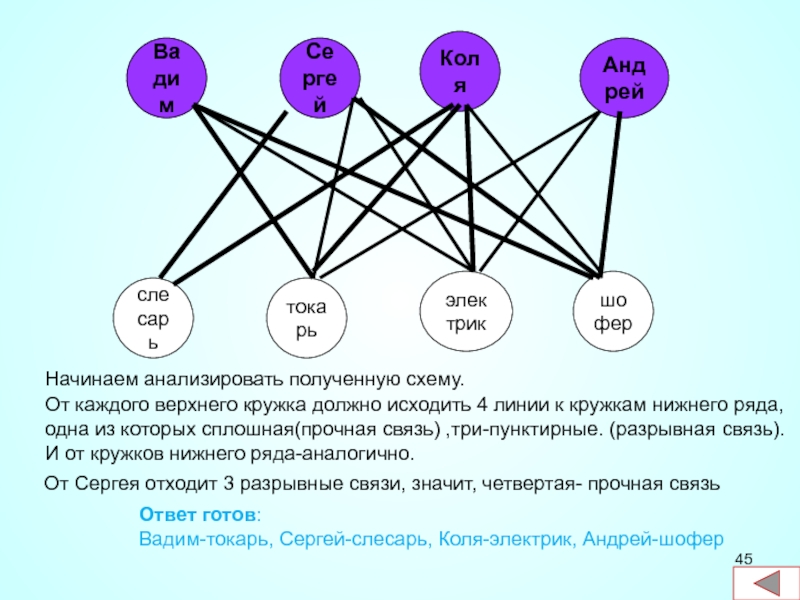
Начинаем анализировать полученную схему.
От каждого верхнего кружка должно исходить 4 линии
От Сергея отходит 3 разрывные связи, значит, четвертая- прочная связь
Ответ готов:
Вадим-токарь, Сергей-слесарь, Коля-электрик, Андрей-шофер
Слайд 46Андрей, Борис, Володя, Даша, Галя договорились созвониться по телефону о посещении
Задача.