- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Теорема о трёх перпендикулярах. Задачи на готовых чертежах презентация
Содержание
- 1. Теорема о трёх перпендикулярах. Задачи на готовых чертежах
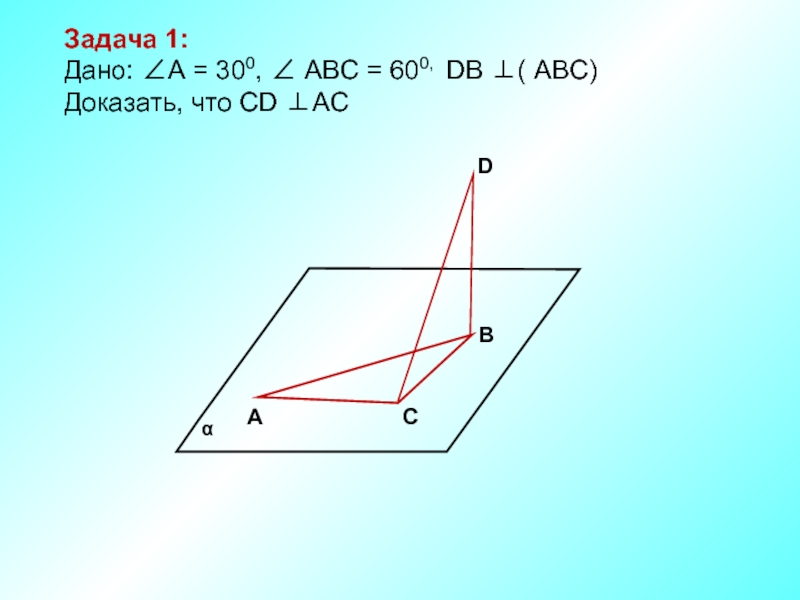
- 2. А С В D
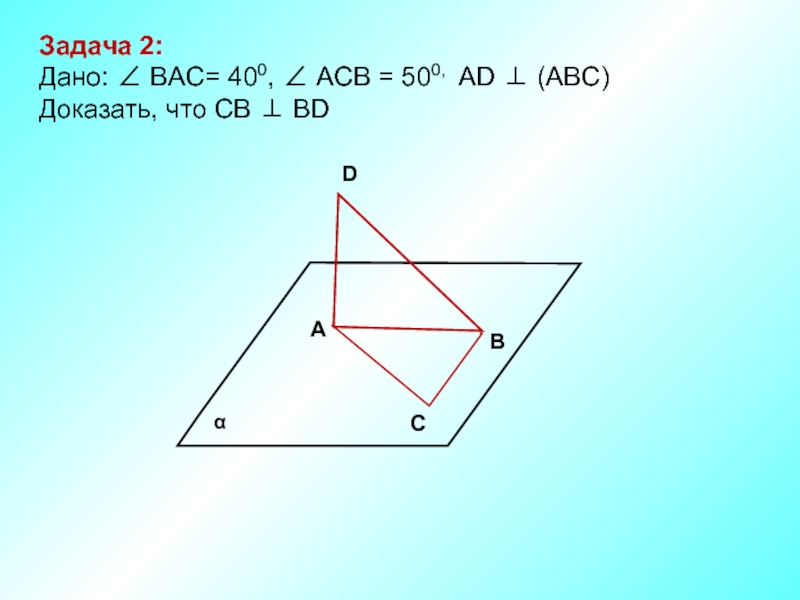
- 3. В D А С
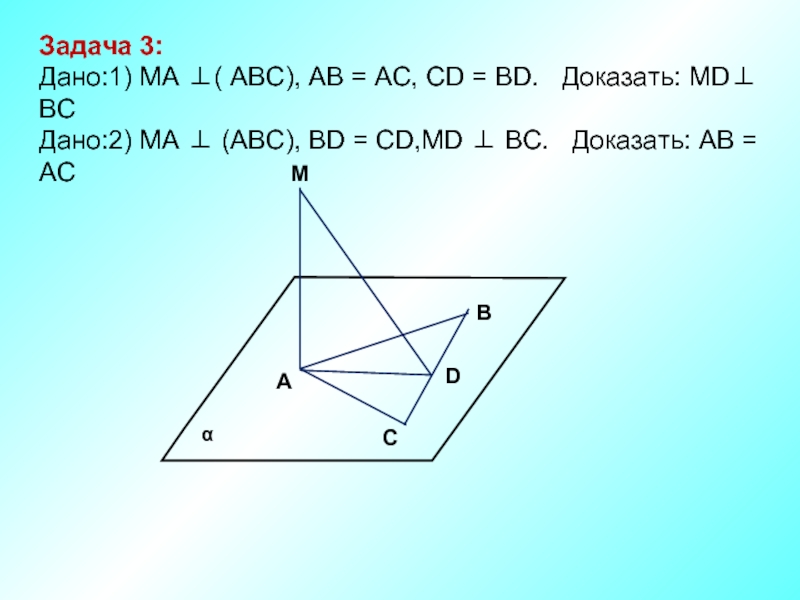
- 4. M В D A C Задача
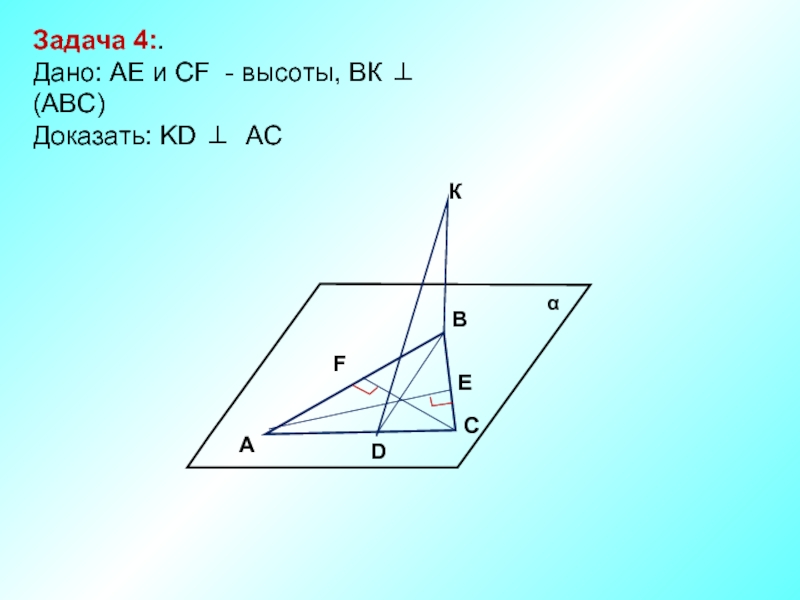
- 5. К В
- 6. M D C A B Задача 5:
- 7. M C D O A
- 8. Задача 7: Дано:Δ ABC, ВD ⊥
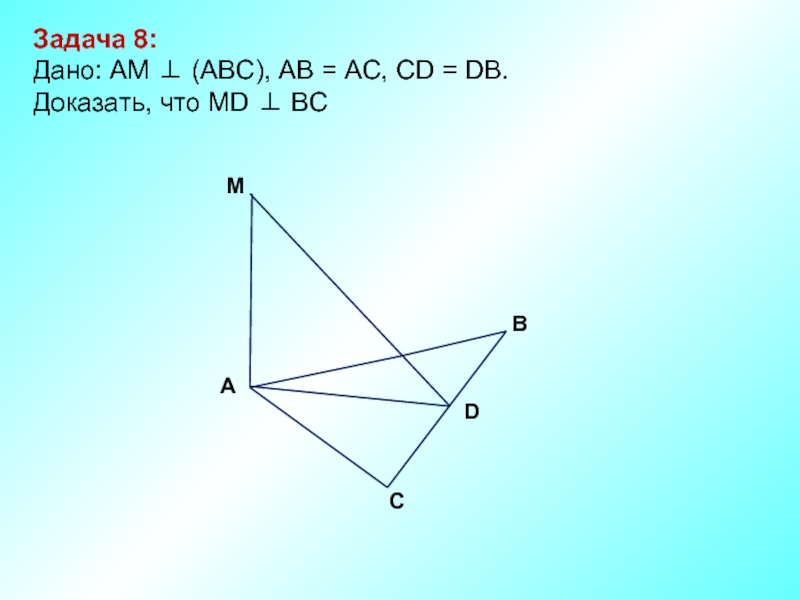
- 9. Задача 8: Дано: АМ ⊥ (АВС),
- 10. Задача 9: Дано: Δ ABC, ∠
- 11. Задача 10: Дано: Δ АBC, AB
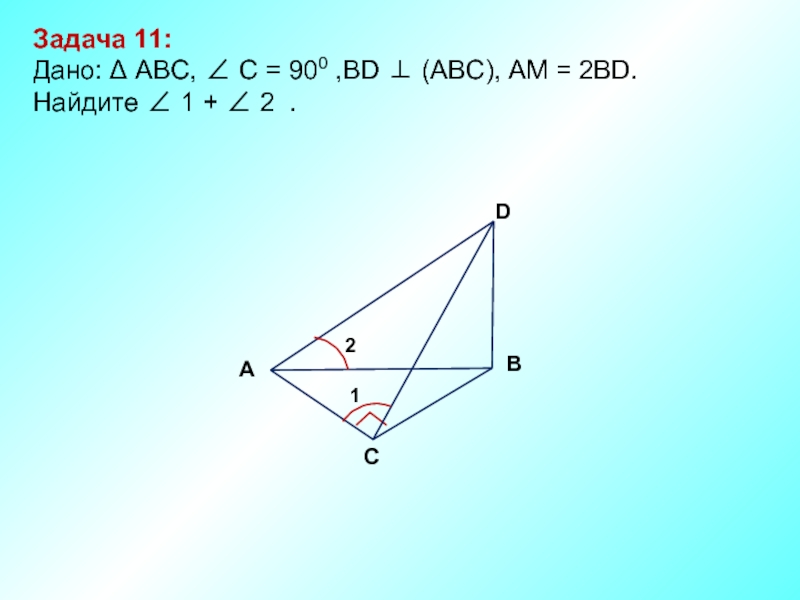
- 12. Задача 11: Дано: Δ АBC, ∠
- 13. D В С А F O
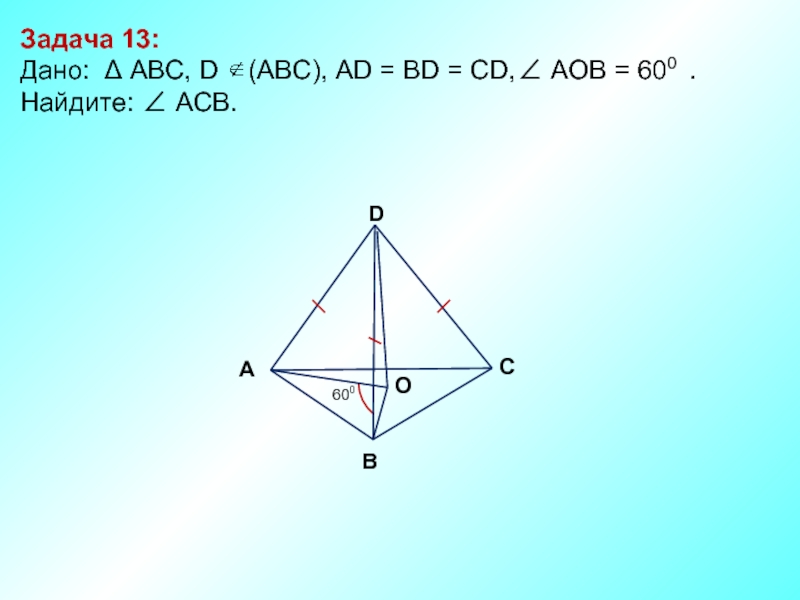
- 14. Задача 13: Дано: Δ АBC, D
- 15. Задача 14: Дано: Δ АBC, AB
- 16. Задача 15: Дано: Δ АBC, ∠
- 17. Задача 16: Дано: Δ АBC, AB
- 18. Задача 17: Дано: Δ АBC, AC
- 19. Литература 1. Ковалёва Г.И. Геометрия 10
А С В D Задача 1: Дано: ∠А = 300, ∠ АВС = 600, DВ ⊥( АВС) Доказать, что СD ⊥АС α
Слайд 4
M
В
D
A
C
Задача 3:
Дано:1) MA ⊥( АВС), AB = AC, CD = BD.
Доказать: MD⊥ ВС
Дано:2) МА ⊥ (АВС), BD = CD,MD ⊥ BC. Доказать: АВ = АС
Дано:2) МА ⊥ (АВС), BD = CD,MD ⊥ BC. Доказать: АВ = АС
α
Слайд 6M
D
C
A
B
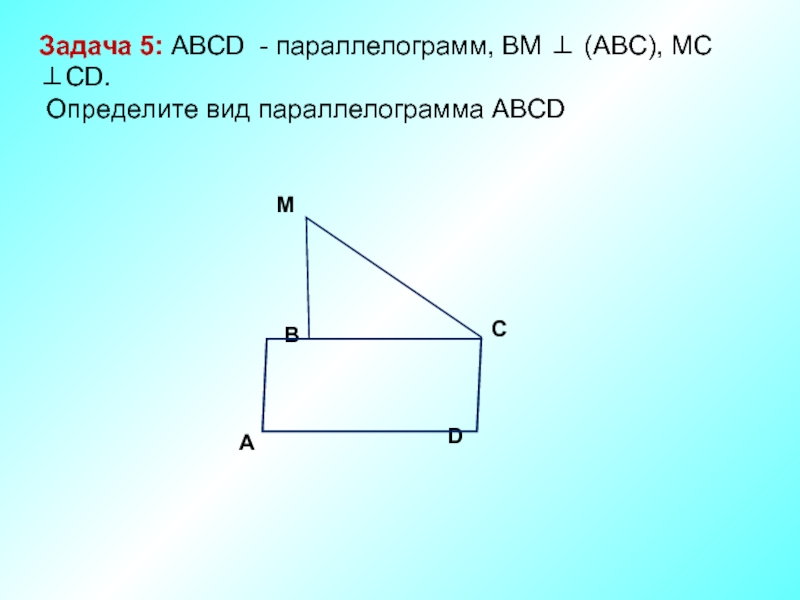
Задача 5: ABCD - параллелограмм, ВМ ⊥ (АВС), МС ⊥СD.
Определите
вид параллелограмма АВСD
Слайд 7
M
C
D
O
A
B
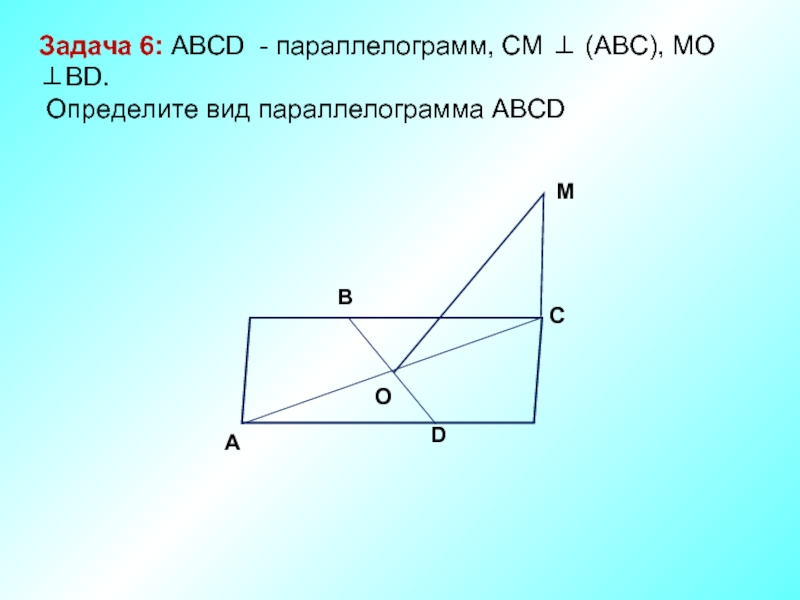
Задача 6: ABCD - параллелограмм, СМ ⊥ (АВС), МО ⊥ВD.
Определите
вид параллелограмма АВСD
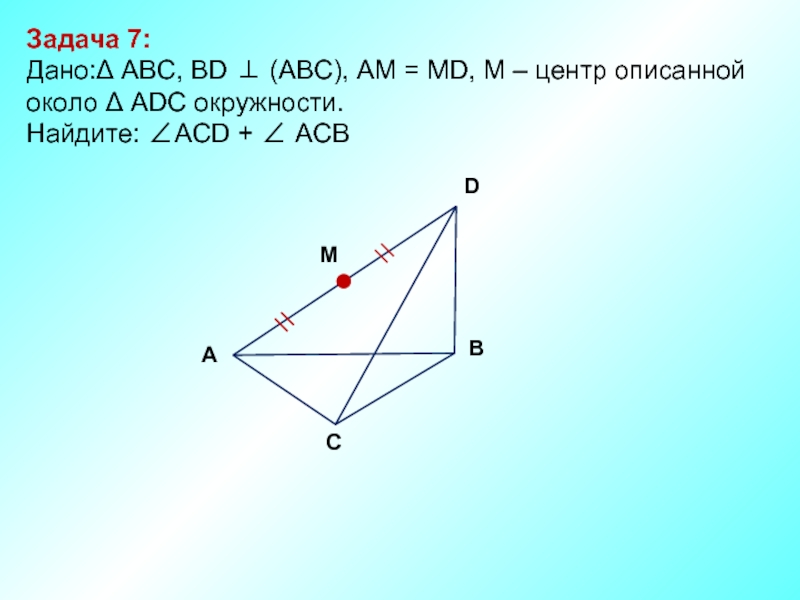
Слайд 8Задача 7:
Дано:Δ ABC, ВD ⊥ (АВС), АМ = МD, М
– центр описанной около Δ ADC окружности.
Найдите: ∠АCD + ∠ АCВ
Найдите: ∠АCD + ∠ АCВ
М
D
В
С
А
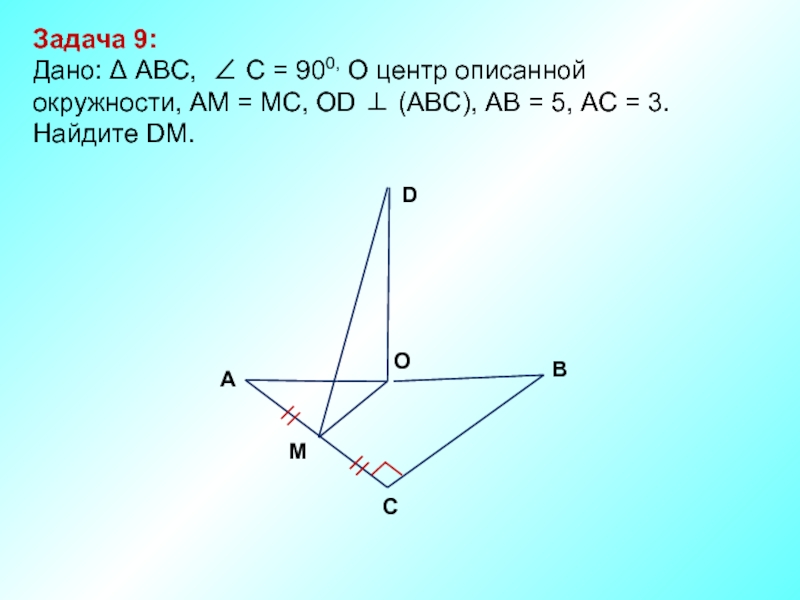
Слайд 10Задача 9:
Дано: Δ ABC, ∠ С = 900, О центр
описанной окружности, АМ = МС, ОD ⊥ (АВС), АВ = 5, АС = 3.
Найдите DM.
Найдите DM.
М
D
В
С
А
O
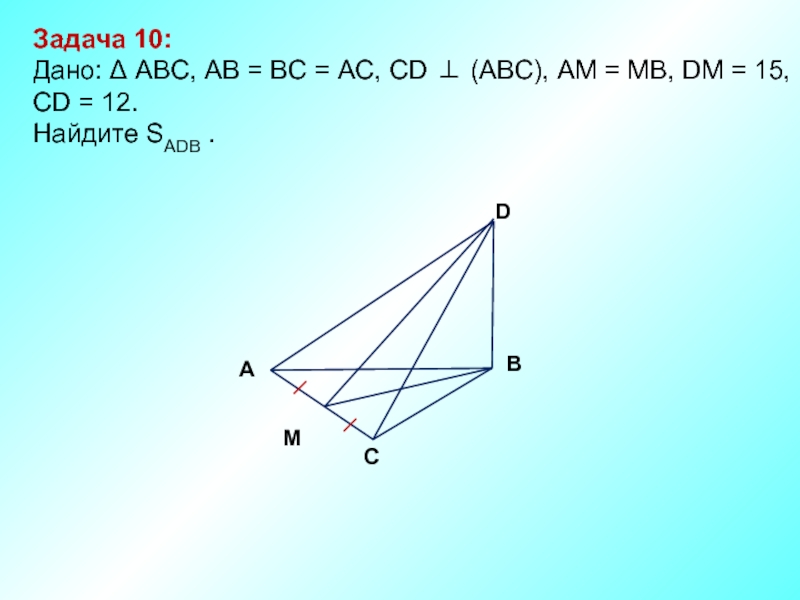
Слайд 11Задача 10:
Дано: Δ АBC, AB = BC = AC, CD
⊥ (АВС), АM = MB, DM = 15, CD = 12.
Найдите SADB .
Найдите SADB .
М
D
В
С
А
Слайд 13D
В
С
А
F
O
450
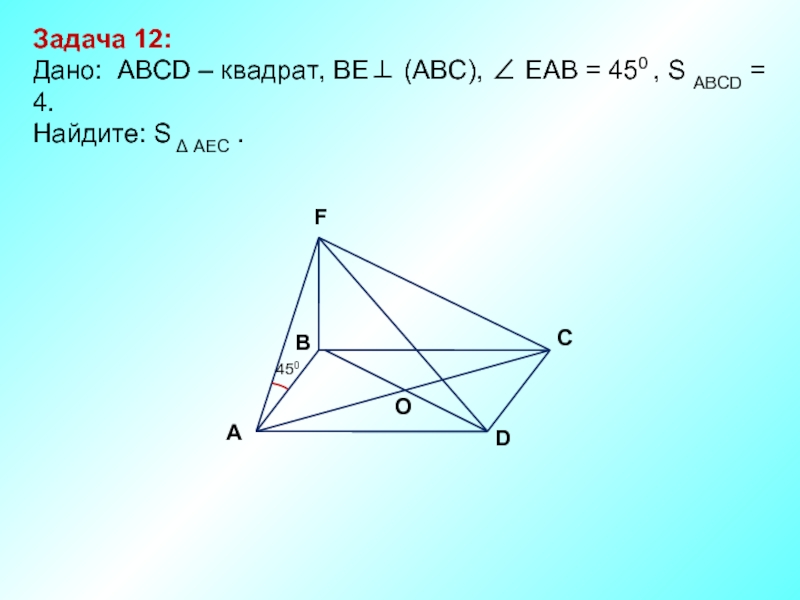
Задача 12:
Дано: АBCD – квадрат, ВЕ⊥ (АВС), ∠ ЕАВ =
450 , S ABCD = 4.
Найдите: S Δ AEC .
Найдите: S Δ AEC .
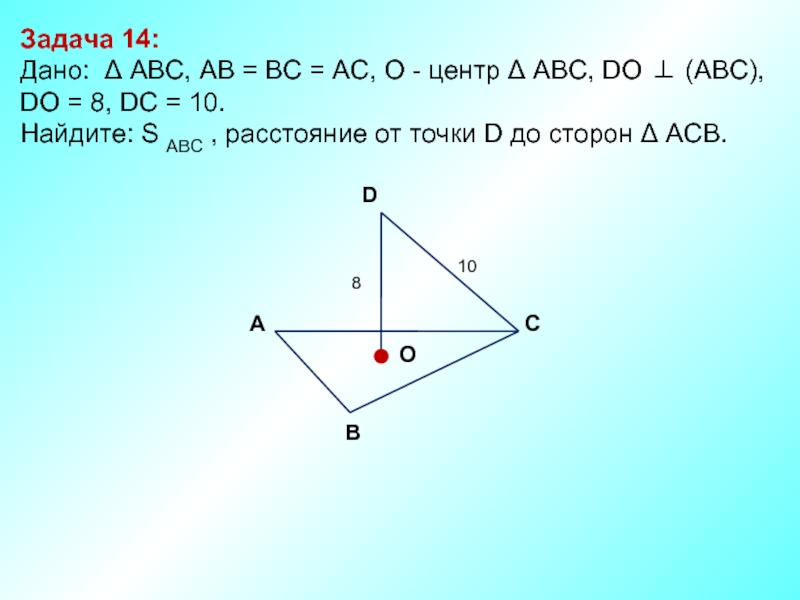
Слайд 15Задача 14:
Дано: Δ АBC, AB = BC = AC, О
- центр Δ АBC, DO ⊥ (АВС), DО = 8, DC = 10.
Найдите: S ABC , расстояние от точки D до сторон Δ ACB.
Найдите: S ABC , расстояние от точки D до сторон Δ ACB.
D
В
С
А
O
10
8
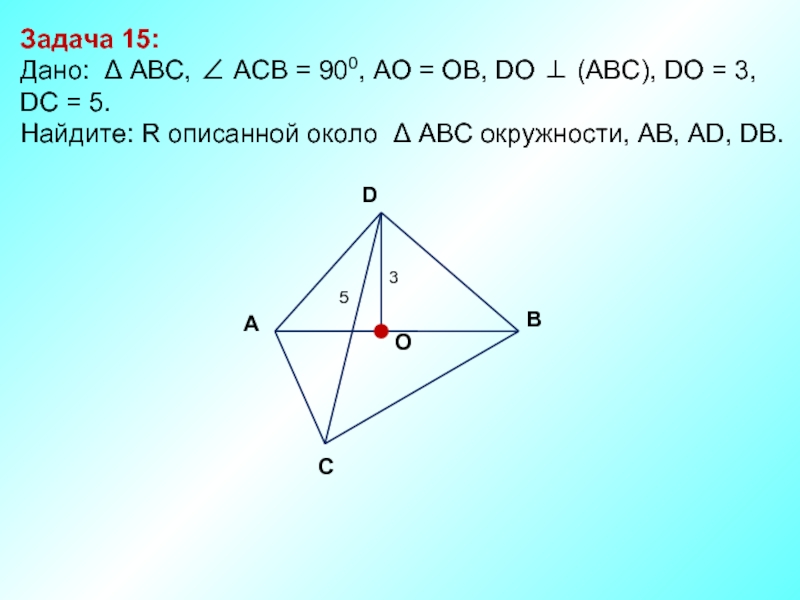
Слайд 16Задача 15:
Дано: Δ АBC, ∠ АСВ = 900, AО =
ОB, DО ⊥ (АВС), DО = 3,
DC = 5.
Найдите: R описанной около Δ AВС окружности, АВ, АD, DB.
DC = 5.
Найдите: R описанной около Δ AВС окружности, АВ, АD, DB.
D
В
С
А
O
3
5
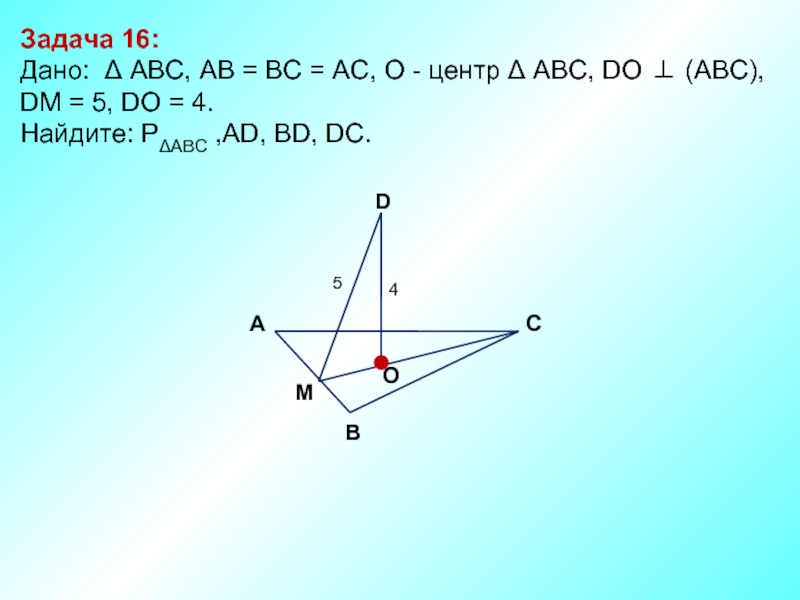
Слайд 17Задача 16:
Дано: Δ АBC, AB = BC = AC, О
- центр Δ АBC, DO ⊥ (АВС), DM = 5, DO = 4.
Найдите: PΔABC ,AD, BD, DC.
Найдите: PΔABC ,AD, BD, DC.
D
В
С
А
O
4
5
M
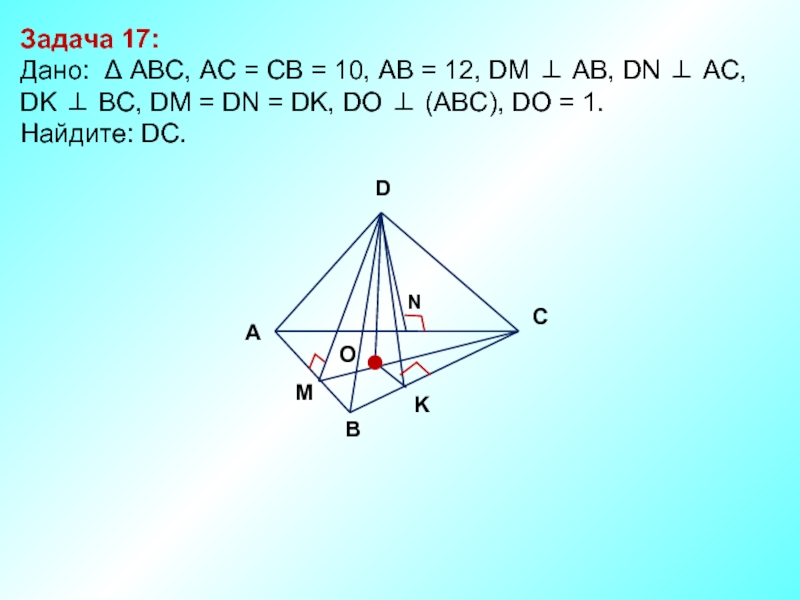
Слайд 18Задача 17:
Дано: Δ АBC, AC = CB = 10, AB
= 12, DM ⊥ АВ, DN ⊥ AC,
DK ⊥ BC, DM = DN = DK, DO ⊥ (ABC), DO = 1.
Найдите: DC.
DK ⊥ BC, DM = DN = DK, DO ⊥ (ABC), DO = 1.
Найдите: DC.
D
В
С
А
O
M
N
K
Слайд 19Литература
1. Ковалёва Г.И. Геометрия 10 класса поурочные планы по учебнику
Атанасян Л.С., Бутузов В.Ф., Кадомцев С.Б., Киселёва Л.С. и др. Волгоград:
Учитель, 2005.
2. Геометрия 10 – 11 Атанасян Л.С., Бутузов В.Ф., Кадомцев С.Б., Киселёва Л.С.,
Позняк Э.Г.,М.: Просвещение, 2008.
