- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
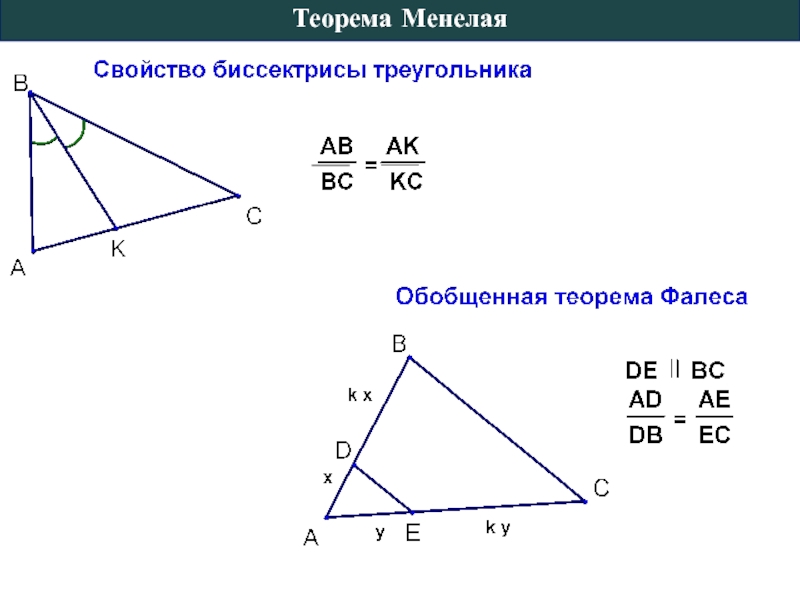
Теорема Менелая презентация
Содержание
- 1. Теорема Менелая
- 2. Теорема Менелая
- 3. Теорема Менелая
- 4. Задача 1. Дан треугольник АВС. На продолжении
- 5. Теорема Менелая. Пусть прямая пересекает стороны ВС,
- 6. Доказательство. внешние односторонние
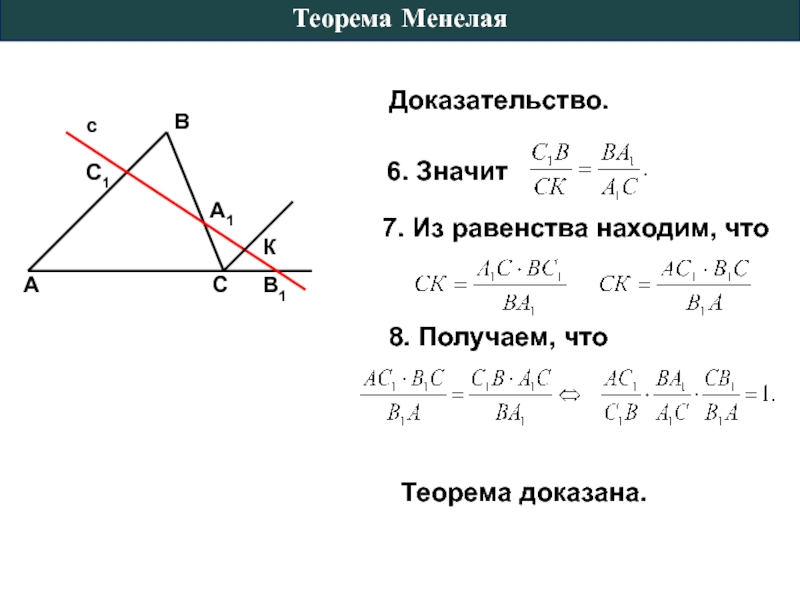
- 7. Теорема доказана. Доказательство. Теорема Менелая 7. Из равенства находим, что 8. Получаем, что
- 8. Теорема Менелая
- 9. Задача 1. Дан треугольник АВС. На продолжении
- 10. Задача 2. В трапеции АВСD основание АD
- 11. Задача 3. В треугольнике АВС на стороне
- 12. Задача 3. В треугольнике АВС на стороне
- 13. Задача 4. В треугольнике АВС, описанном около
- 14. Задача 4. В треугольнике АВС, описанном около
- 15. Теорема Менелая Домашнее
Слайд 4Задача 1. Дан треугольник АВС. На продолжении стороны АС за точку
В каком отношении прямая MN делит сторону АВ?
a
2a
x
3x
1. Проведем прямую ВТ ││ AN.
Т
2. Пусть CN = a, AC = 2a.
Δ TBM подобен Δ NCM по двум углам.
TB : NC = BM : MC = 1 : 3, .
3. Δ TBK подобен Δ NAK по двум углам.
ВК : KA = TB : NA = 1 : 9.
Теорема Менелая
Решение.
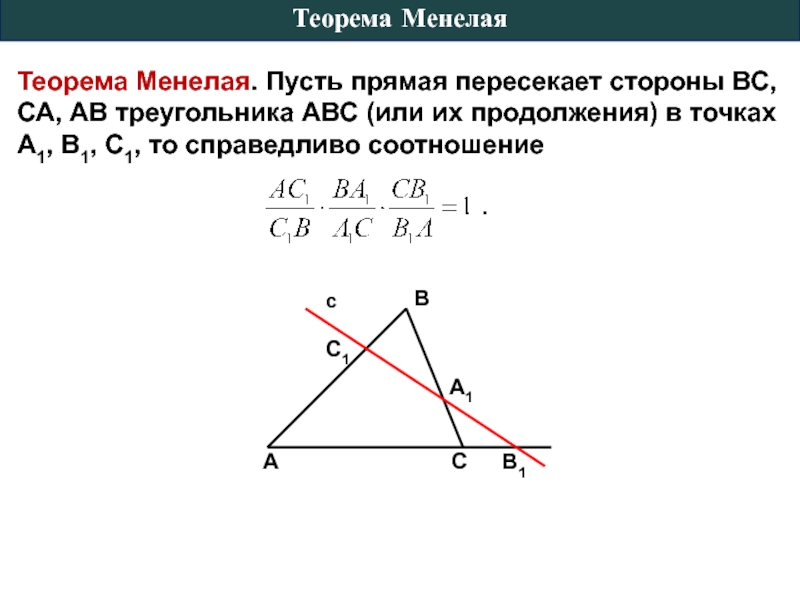
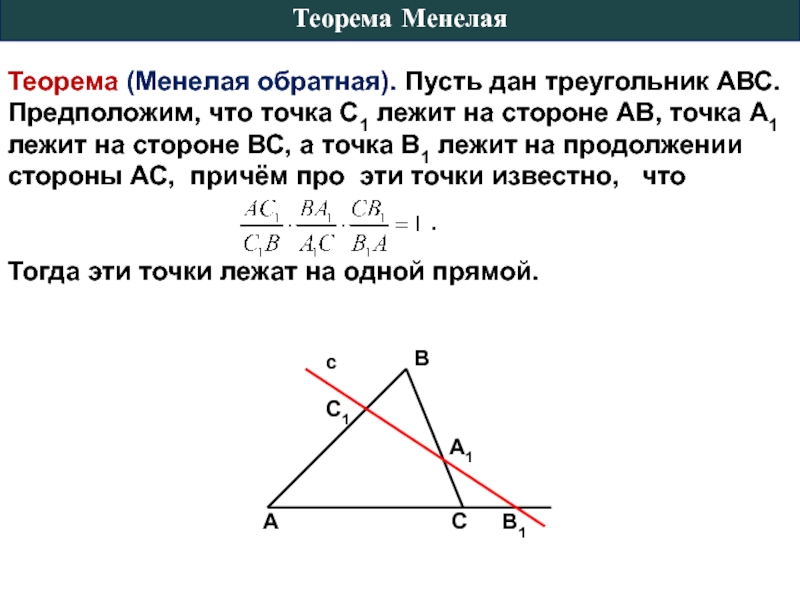
Слайд 5Теорема Менелая. Пусть прямая пересекает стороны ВС, СА, АВ треугольника АВС
Теорема Менелая
Слайд 6
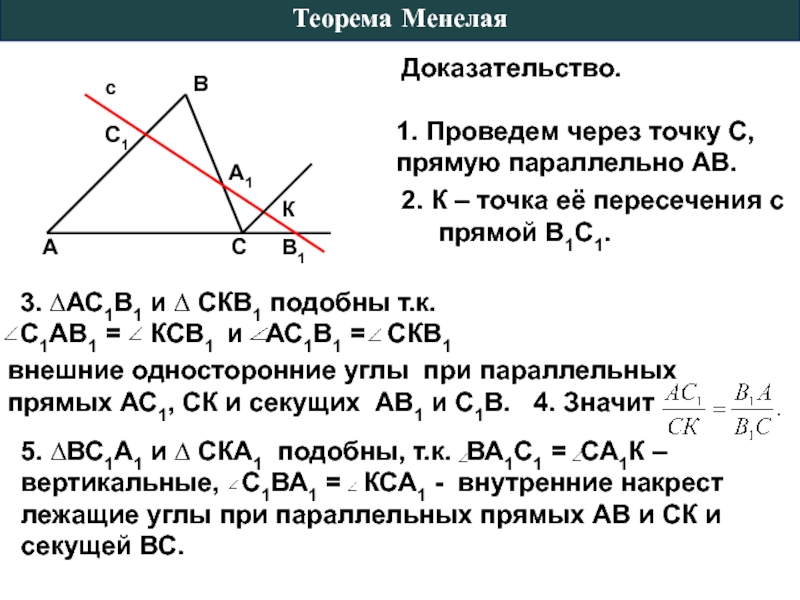
Доказательство.
внешние односторонние углы при параллельных
прямых АС1, СК и секущих АВ1
4. Значит
Теорема Менелая
1. Проведем через точку С, прямую параллельно АВ.
2. К – точка её пересечения с
прямой В1С1.
Слайд 9Задача 1. Дан треугольник АВС. На продолжении стороны АС за точку
В каком отношении прямая MN делит сторону АВ?
a
2a
x
3x
Решение.
Теорема Менелая
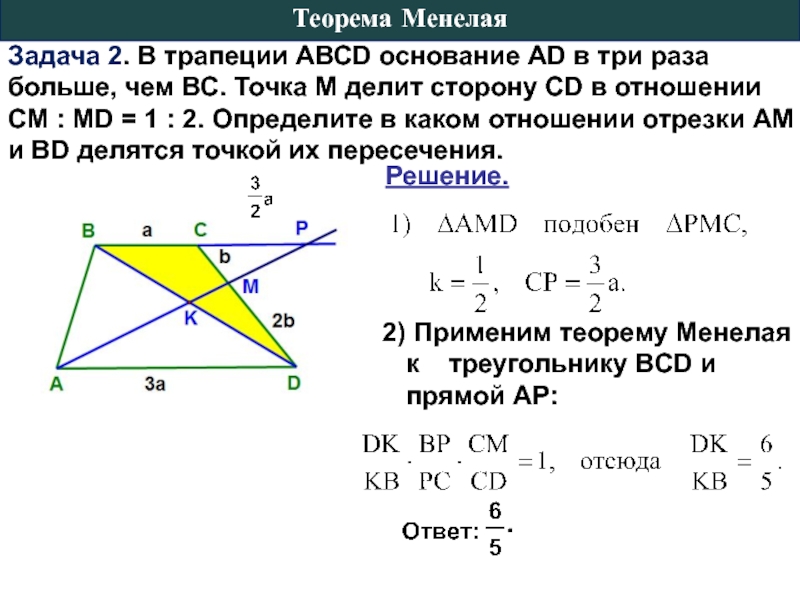
Слайд 10Задача 2. В трапеции АВСD основание АD в три раза больше,
Решение.
Теорема Менелая
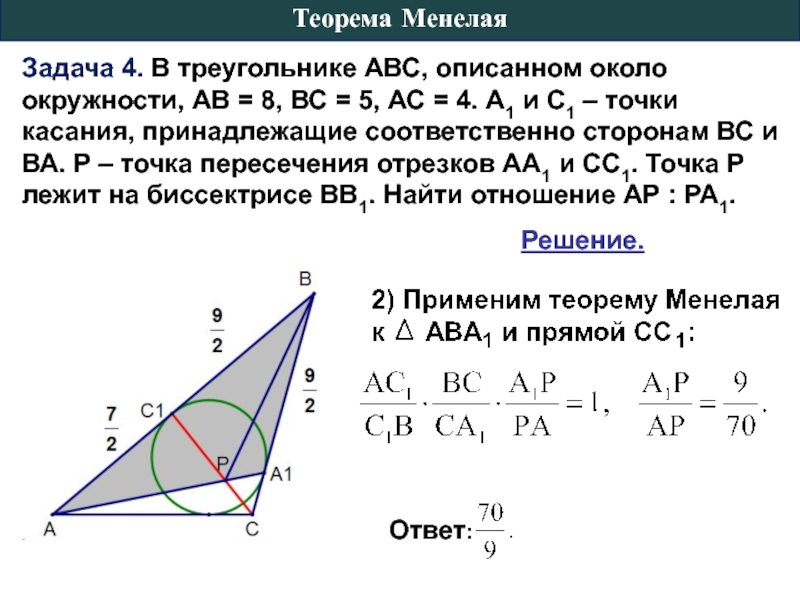
2) Применим теорему Менелая к треугольнику ВCD и прямой АР:
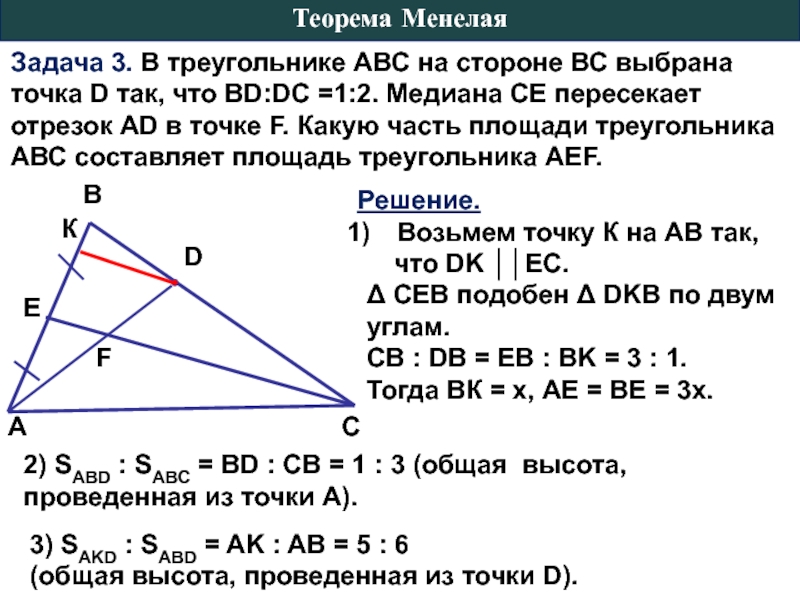
Слайд 11Задача 3. В треугольнике АВС на стороне ВС выбрана точка D
E
Решение.
Возьмем точку К на АВ так,
что DK ││ЕC.
Δ СЕВ подобен Δ DKB по двум углам.
СВ : DB = EB : BK = 3 : 1.
Тогда ВК = х, АЕ = ВЕ = 3х.
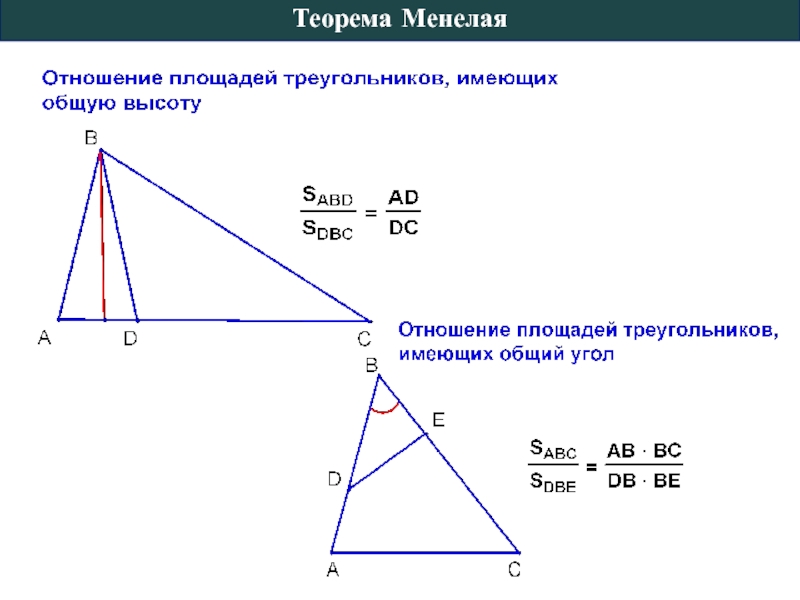
2) SABD : SABC = BD : CB = 1 : 3 (общая высота, проведенная из точки А).
3) SAKD : SABD = AK : AB = 5 : 6
(общая высота, проведенная из точки D).
Теорема Менелая
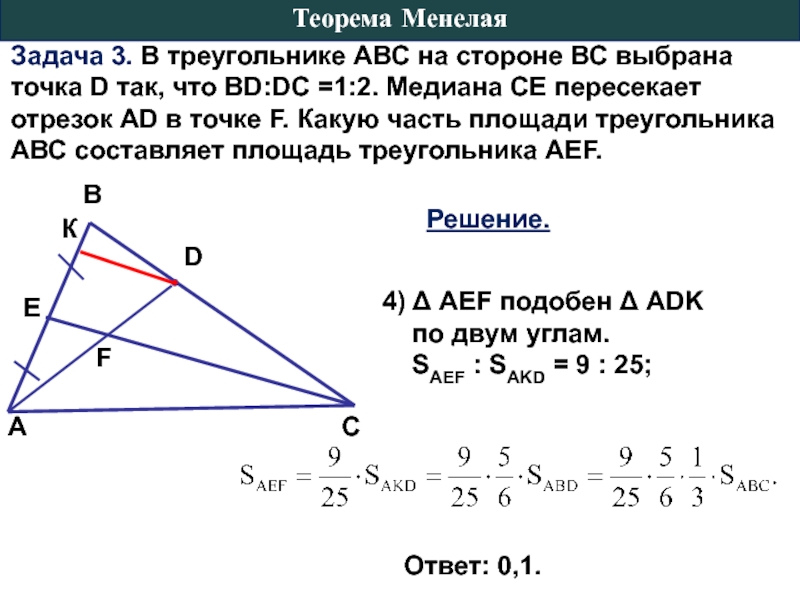
Слайд 12Задача 3. В треугольнике АВС на стороне ВС выбрана точка D
E
Решение.
4) Δ AEF подобен Δ ADK
по двум углам.
SAEF : SAKD = 9 : 25;
Ответ: 0,1.
Теорема Менелая
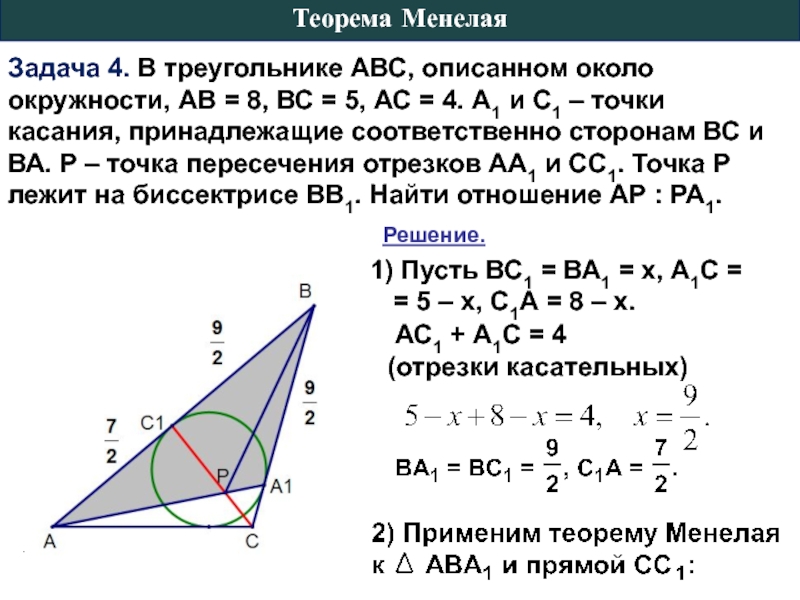
Слайд 13Задача 4. В треугольнике АВС, описанном около окружности, АВ = 8,
х
х
5 – х
8 – х
4
Теорема Менелая
Решение.
1) Пусть ВС1 = ВА1 = х, А1С = = 5 – х, С1А = 8 – х.
АС1 + А1С = 4
(отрезки касательных)
Слайд 14Задача 4. В треугольнике АВС, описанном около окружности, АВ = 8,
х
х
5 – х
8 – х
4
Теорема Менелая
Решение.
Слайд 15
Теорема Менелая
Домашнее задание.
3. Докажите, что медианы треугольника пересекаются
2. В треугольнике АВС угол С – прямой, ВС = 3, АС = 4 и проведены биссектриса СD и медиана АМ. Найти площадь треугольника СЕМ.
Дан треугольник АВС, в котором ВМ – медиана. Точка Р лежит на стороне АВ, точка Q – на стороне ВС, причем
Отрезок PQ пересекает медиану ВМ в точке R.
Найти