- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Тени в ортогональных проекциях презентация
Содержание
- 1. Тени в ортогональных проекциях
- 2. Назначение теней Тени позволяют компенсировать отсутствие третьего
- 3. Назначение теней
- 4. Назначение теней
- 5. Основные понятия Для построения тени необходимы:
- 6. Основные понятия освещаемый объект (Φ);
- 7. Основные понятия поверхность, на которую будет падать тень (Π′).
- 8. Основные понятия источник
- 9. Основные понятия Собственной тенью называют тень, которая
- 10. Основные понятия Контуром собственной тени называют линию
- 11. Основные понятия Падающей тенью называют тень, отбрасываемую объектом Φ на какую-либо поверхность Π′.
- 12. Основные понятия Контуром падающей тени называют линию, ограничивающую падающую тень (m′).
- 13. Основные понятия Контур падающей тени является тенью
- 14. Выбор направления световых лучей При построении теней в ортогональных проекциях выбирают естественное освещение.
- 15. Выбор направления световых лучей Для естественного освещения
- 16. Выбор направления световых лучей Проекции светового луча
- 17. Построение тени точки Тень точки строится как
- 18. Построение тени точки Через проекции точек А
- 19. Построение тени точки Тень от точки В
- 20. Построение тени линии Для построения тени линии
- 21. Построение тени линии Тени концов отрезка АВ
- 22. Построение тени линии Тени концов отрезка CD
- 23. Построение тени линии Тени от прямых частного
- 24. Построение тени линии AB перпендикулярна П₁ CD перпендикулярна П₂
- 25. Построение тени линии АВ || П₁, A₁tB₁t=A₁B₁,
- 26. Построение тени линии Для построения тени от
- 27. Построение тени линии
- 28. Построение тени плоской фигуры Форма падающей от
- 29. Тени плоских фигур Тень, падающая на плоскость
- 30. Тени плоских фигур Тень фигуры, параллельной горизонтальной плоскости Тень фигуры, параллельной фронтальной плоскости
- 31. Тени плоских фигур Тень на плоскость, не
- 32. Тени плоских фигур
- 33. Тени геометрических тел Построение теней геометрических тел
- 34. Тени геометрических тел (тень призмы на горизонтальную
- 35. Тени геометрических тел (тень призмы на горизонтальную
- 36. Тени геометрических тел (тень призмы на горизонтальную
- 37. Тени геометрических тел (тень призмы на горизонтальную
- 38. Тени геометрических тел (тень призмы на вертикальную
- 39. Тени геометрических тел (тень призмы на вертикальную
- 40. Тени геометрических тел (тень призмы на вертикальную
- 41. Тени геометрических тел (тень призмы на вертикальную
- 42. Тени геометрических тел (тень цилиндра) Собственная тень
- 43. Тени геометрических тел (тень цилиндра) Построение падающей
- 44. Тени геометрических тел (тень цилиндра) Между нижним
- 45. Тени геометрических тел (тень конуса) Собственная тень
- 46. Тени геометрических тел (тень цилиндра) Построение падающей тени начинают с построения тени от вершины конуса.
- 47. Тени геометрических тел (тень цилиндра) Из точки
- 48. Тени архитектурных фрагментов
- 49. Тени архитектурных фрагментов (алгоритм построения) Построение теней
- 50. Тени архитектурных фрагментов (тени в нишах) Тень
- 51. Тени архитектурных фрагментов (тени в нишах) Тень
- 52. Тени архитектурных фрагментов (тени в нишах) Тень
- 53. Тени архитектурных фрагментов (тени от козырьков) Тень
- 54. Тени архитектурных фрагментов (тени от козырьков) Тень
- 55. Тени архитектурных фрагментов (тени козырьков) Тень, падающая
- 56. Тени архитектурных фрагментов (тени козырьков) 3. Проекция
- 57. Тени архитектурных фрагментов (тени козырьков) Тень, падающая
- 58. Тени архитектурных фрагментов (тени козырьков) 3. тени
- 59. Тени архитектурных фрагментов (тени на лестнице) При
- 60. Тени архитектурных фрагментов (тени на ступеньках) Для
- 61. Тени архитектурных фрагментов (тени на ступеньках) Для
- 62. Тени архитектурных фрагментов (тени на ступеньках)
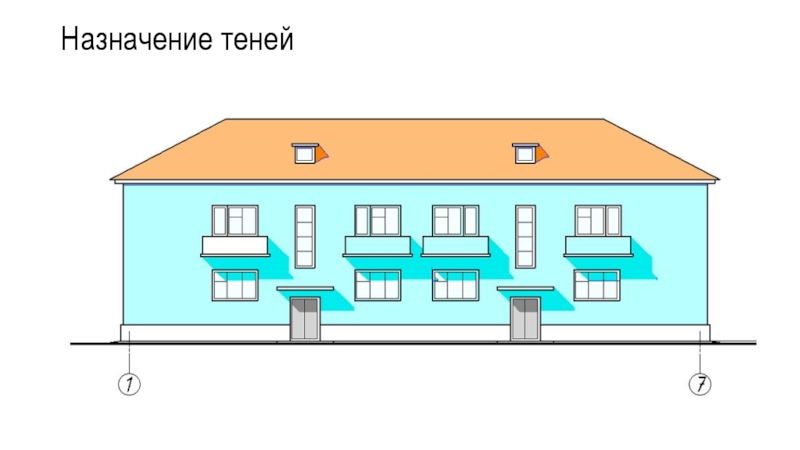
Слайд 2Назначение теней
Тени позволяют компенсировать отсутствие третьего измерения на горизонтальной проекции (плане)
и фронтальной проекции (фасаде) проектируемого объекта.
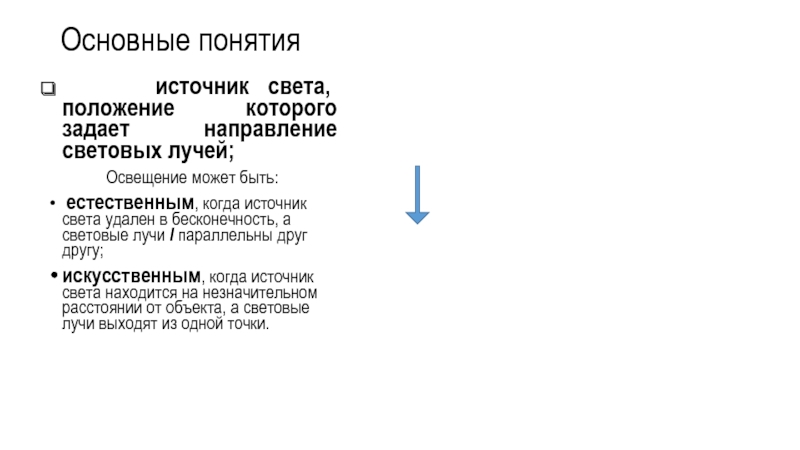
Слайд 8Основные понятия
источник света, положение которого задает направление
световых лучей;
Освещение может быть:
естественным, когда источник света удален в бесконечность, а световые лучи l параллельны друг другу;
искусственным, когда источник света находится на незначительном расстоянии от объекта, а световые лучи выходят из одной точки.
Освещение может быть:
естественным, когда источник света удален в бесконечность, а световые лучи l параллельны друг другу;
искусственным, когда источник света находится на незначительном расстоянии от объекта, а световые лучи выходят из одной точки.
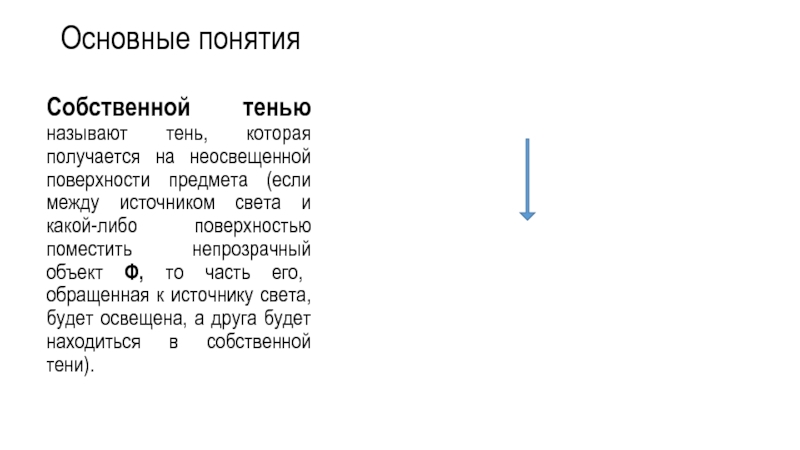
Слайд 9Основные понятия
Собственной тенью называют тень, которая получается на неосвещенной поверхности предмета
(если между источником света и какой-либо поверхностью поместить непрозрачный объект Φ, то часть его, обращенная к источнику света, будет освещена, а друга будет находиться в собственной тени).
Слайд 10Основные понятия
Контуром собственной тени называют линию (m), отделяющую освещенную поверхность предмета
от неосвещенной.
Слайд 11Основные понятия
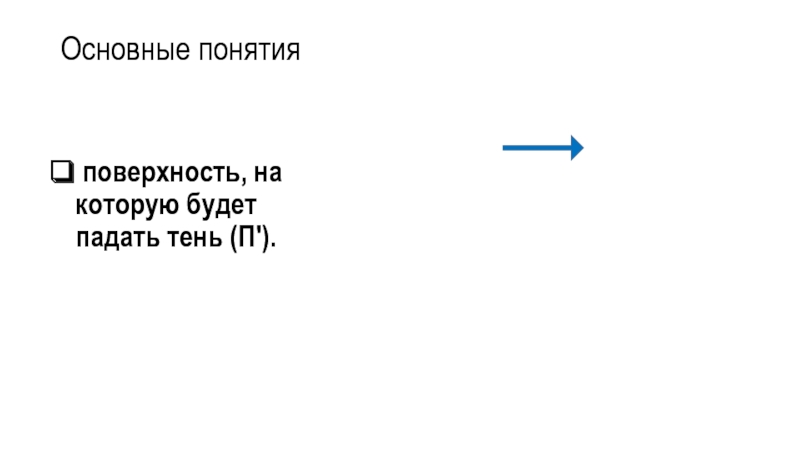
Падающей тенью называют тень, отбрасываемую объектом Φ на какую-либо поверхность
Π′.
Слайд 13Основные понятия
Контур падающей тени является тенью контура собственной тени.
Контуры собственной и
падающей теней всегда являются замкнутыми линиями.
При построении теней в первую очередь определяют собственную тень и контур собственной тени.
Тень, падающая на поверхность от точки или линии, принадлежащей этой поверхности, совпадает с самой точкой или линией.
Контур падающей тени m′ строят как точку или линию пересечения светового луча l (или световой поверхности), проходящей через контур собственной тени m, с плоскостью или поверхностью Π′, на которой строится тень.
При построении теней в первую очередь определяют собственную тень и контур собственной тени.
Тень, падающая на поверхность от точки или линии, принадлежащей этой поверхности, совпадает с самой точкой или линией.
Контур падающей тени m′ строят как точку или линию пересечения светового луча l (или световой поверхности), проходящей через контур собственной тени m, с плоскостью или поверхностью Π′, на которой строится тень.
Слайд 14Выбор направления световых лучей
При построении теней в ортогональных проекциях выбирают естественное
освещение.
Слайд 15Выбор направления световых лучей
Для естественного освещения направление световых лучей параллельно диагонали
светового куба. Натуральная величина угла наклона этого направления к любой из плоскостей проекций составляет 350 .
Слайд 16Выбор направления световых лучей
Проекции светового луча на горизонтальную и фронтальную плоскости
проекций составляют с осью x1 углы 450.
Слайд 17Построение тени точки
Тень точки строится как точка пересечения светового луча, проходящего
через эту точку с плоскостью или поверхностью. Такая тень может быть действительной (истинной) и мнимой.
Условие задачи:
Заданы проекции точек А (А1 и А2) и В (В1 и В2), положение оси х12 и проекции светового луча l (l1 и l2). Построить тени точек на горизонтальную и вертикальную плоскости.
Условие задачи:
Заданы проекции точек А (А1 и А2) и В (В1 и В2), положение оси х12 и проекции светового луча l (l1 и l2). Построить тени точек на горизонтальную и вертикальную плоскости.
Слайд 18Построение тени точки
Через проекции точек А и В проводят проекции световых
лучей и определяют точки пересечения их с плоскостями проекций (осью х1).
Тень от точки упадет на горизонтальную плоскость, если проекция светового луча l2 пересечет ось х1 раньше (левее), чем проекция l1 (тень точки А)
Если ось х1 первой пересечет проекция l1, то тень от точки упадет на вертикальную плоскость (тень точки В).
Эти тени будут истинными.
Тень от точки упадет на горизонтальную плоскость, если проекция светового луча l2 пересечет ось х1 раньше (левее), чем проекция l1 (тень точки А)
Если ось х1 первой пересечет проекция l1, то тень от точки упадет на вертикальную плоскость (тень точки В).
Эти тени будут истинными.
Слайд 19Построение тени точки
Тень от точки В на горизонтальной плоскости будет истинной,
а на фронтальную мнимой.
Слайд 20Построение тени линии
Для построения тени линии в общем случая необходимо и
достаточно построить тени точек, принадлежащих этой линии.
Слайд 21Построение тени линии
Тени концов отрезка АВ находятся на одной плоскости проекций.
Тень – прямая линия. Для построения тени прямой в данном случае достаточно соединить полученные тени точек.
Слайд 22Построение тени линии
Тени концов отрезка CD находятся на разных плоскостях проекций,
тень – ломаная линия.
Для построения тени необходимо построить тени концов отрезка на одну плоскость проекций, причем одна тень будет истинной, а вторая мнимой и проводят через полученные точки прямую. Точка пересечения этой прямой с осью будет точкой излома.
Для построения тени необходимо построить тени концов отрезка на одну плоскость проекций, причем одна тень будет истинной, а вторая мнимой и проводят через полученные точки прямую. Точка пересечения этой прямой с осью будет точкой излома.
Слайд 23Построение тени линии
Тени от прямых частного положения:
Тень от прямой перпендикулярной плоскости
или поверхности совпадает с проекцией светового луча на эту плоскость.
Тень от линии, параллельной плоскости, равна и параллельна самой этой линии. Для построения тени прямой линии достаточно построить тень одной ее точки.
Тень от линии, параллельной плоскости, равна и параллельна самой этой линии. Для построения тени прямой линии достаточно построить тень одной ее точки.
Слайд 25Построение тени линии
АВ || П₁, A₁tB₁t=A₁B₁, A₁tB₁tǁA₁B₁
CD || П₂, C₂tD₂t
= C₂D₂, C₂tD₂t ǁ C₂D₂
Слайд 26Построение тени линии
Для построения тени от прямой на плоскость общего положения
необходимо и достаточно построить точки пересечения световых лучей, проведенных через концы отрезка с этой плоскостью по общему алгоритму построения точки пересечения прямой общего положения с плоскостью общего положения.
Слайд 28Построение тени плоской фигуры
Форма падающей от плоской фигуры тени зависит от
формы самой фигуры, от формы поверхности, на которую эта тень падает, и взаимного расположения плоской фигуры и поверхности.
Слайд 29Тени плоских фигур
Тень, падающая на плоскость от параллельной этой плоскости фигуры,
равна и параллельна самой этой фигуре, поэтому достаточно найти тень одной точки фигуры и построить фигуру, равную той, от которой строим тень.
Слайд 30Тени плоских фигур
Тень фигуры, параллельной горизонтальной плоскости
Тень фигуры, параллельной фронтальной плоскости
Слайд 31Тени плоских фигур
Тень на плоскость, не параллельную заданной фигуре, строиться как
совокупность теней характерных точек плоской фигуры.
Слайд 33Тени геометрических тел
Построение теней геометрических тел выполняется по следующему алгоритму:
определяют
собственную тень геометрического тела;
определяют контур собственной тени геометрического тела;
строят тень контура по рассмотренным выше правилам, причем сначала строят тень от линии, перпендикулярной плоскости или поверхности, а затем от линий, параллельных плоскости или поверхности.
определяют контур собственной тени геометрического тела;
строят тень контура по рассмотренным выше правилам, причем сначала строят тень от линии, перпендикулярной плоскости или поверхности, а затем от линий, параллельных плоскости или поверхности.
Слайд 34Тени геометрических тел (тень призмы на горизонтальную плоскость)
В собственной тени правильной
четырехгранной призмы (параллелепипеда) находятся задняя (B′BCC′) и правая боковая (А′АВВ′) грани призмы. Ломаная линия A′ABCC′B′A′ является контуром собственной тени.
Слайд 35Тени геометрических тел (тень призмы на горизонтальную плоскость)
Построение падающей тени начинают
с построения ближайшей к наблюдателю и самой высокой точки, в настоящем примере это точка В.
Слайд 36Тени геометрических тел (тень призмы на горизонтальную плоскость)
Далее последовательно строят тени
от прямых ВС и CD, параллельных плоскости проекций, их тени будут равны и параллельны самим отрезкам.
Слайд 37Тени геометрических тел (тень призмы на горизонтальную плоскость)
Тень от линии DD′
будет направлена по проекции светового луча, так как прямая перпендикулярна плоскости, на которую строится тень.
Тени от прямых D′C′ и C′B′ совпадут с проекциями этих прямых, так как прямые лежат в плоскости, на которую строится тень.
Тени от прямых D′C′ и C′B′ совпадут с проекциями этих прямых, так как прямые лежат в плоскости, на которую строится тень.
Слайд 38Тени геометрических тел (тень призмы на вертикальную плоскость)
В собственной тени правильной
четырехгранной призмы (параллелепипеда) находятся нижняя (А′B′C′D′) и правая боковая (А′АВВ′) грани призмы. Ломаная линия A′ABB′C′D′A′ является контуром собственной тени.
Слайд 39Тени геометрических тел (тень призмы на вертикальную плоскость)
Построение падающей тени начинают
с построения ближайшей к наблюдателю и самой высокой точки, в настоящем примере это точка A.
Слайд 40Тени геометрических тел (тень призмы на вертикальную плоскость)
Далее последовательно строят тени
от прямых AA′ и A′D′, параллельных плоскости проекций, их тени будут равны и параллельны самим отрезкам.
Слайд 41Тени геометрических тел (тень призмы на вертикальную плоскость)
Тень от линии D′C′
будет направлена по проекции светового луча, так как прямая перпендикулярна плоскости, на которую строится тень.
Тени от прямых C′B′ и D′A′ совпадут с проекциями этих прямых, так как прямые лежат в плоскости, на которую строится тень.
Тени от прямых C′B′ и D′A′ совпадут с проекциями этих прямых, так как прямые лежат в плоскости, на которую строится тень.
Слайд 42Тени геометрических тел (тень цилиндра)
Собственная тень цилиндра ограничена линией основания и
образующими. Для определения собственной тени боковой поверхности цилиндра необходимо построить точку касания светового луча с этой поверхностью и провести через нее образующую.
Слайд 43Тени геометрических тел (тень цилиндра)
Построение падающей тени начинают с построения тени
от верхнего основания цилиндра.
Слайд 44Тени геометрических тел (тень цилиндра)
Между нижним основанием и полученной тенью верхнего
основания проводят касательные, представляющие собой тени образующих АВ и А′В′, которые являются линиями контура собственной тени.
Слайд 45Тени геометрических тел (тень конуса)
Собственная тень конуса ограничена его образующими. Для
определения собственной тени боковой поверхности конуса необходимо построить точку касания светового луча с основанием и провести через нее образующую.
Слайд 46Тени геометрических тел (тень цилиндра)
Построение падающей тени начинают с построения тени
от вершины конуса.
Слайд 47Тени геометрических тел (тень цилиндра)
Из точки S₁t проводят касательные к основанию
конуса, представляющие собой тени образующих SА и SB, которые являются линиями контура собственной тени конуса.
Слайд 49Тени архитектурных фрагментов (алгоритм построения)
Построение теней архитектурных фрагментов выполняется по следующему
алгоритму:
определяют части поверхностей, находящиеся в собственной тени и контур собственной тени;
строят тень от контура собственной тени по общим правилам построения тени линии и тени геометрического тела.
Внимание: чем ближе к наблюдателю находится поверхность, на которую падает тень, тем эта тень меньше.
определяют части поверхностей, находящиеся в собственной тени и контур собственной тени;
строят тень от контура собственной тени по общим правилам построения тени линии и тени геометрического тела.
Внимание: чем ближе к наблюдателю находится поверхность, на которую падает тень, тем эта тень меньше.
Слайд 50Тени архитектурных фрагментов (тени в нишах)
Тень в прямоугольной плоской нише
Контуром собственной
тени являются ребра АВ и ВС, параллельные фронтальной стенке ниши. Тени этих линий равны и параллельны самим линиям, поэтому для построения тени в нише достаточно определить тень точки В.
Слайд 51Тени архитектурных фрагментов (тени в нишах)
Тень в полуциркульной
плоской нише
Контуром собственной
тени являются прямая АВ и дуга с центром в точке О, параллельные фронтальной стенке ниши. Тени этих линий равны и параллельны самим линиям, поэтому для построения тени в нише достаточно определить тень точки В и центра окружности.
Слайд 52Тени архитектурных фрагментов (тени в нишах)
Тень в цилиндрической нише
Контуром собственной тени
являются прямые АВ и ВС.
Тень прямой АВ совпадает с проекцией оси цилиндра.
Тень от линии ВС - дуга с центром в точке О₂ и радиусом равным радиусу цилиндра.
Тень прямой АВ совпадает с проекцией оси цилиндра.
Тень от линии ВС - дуга с центром в точке О₂ и радиусом равным радиусу цилиндра.
Слайд 53Тени архитектурных фрагментов (тени от козырьков)
Тень от козырька прямоугольной формы на
плоскость строится по тем же правилам, что и тень призмы.
Слайд 54Тени архитектурных фрагментов (тени от козырьков)
Тень от козырька цилиндрической формы на
стену (вертикальную плоскость) строят по следующему алгоритму:
определяют собственную тень и строят контур собственной тени боковой поверхности цилиндра;
Строят проекции контура падающей тени по общим правилам построения тени точки.
определяют собственную тень и строят контур собственной тени боковой поверхности цилиндра;
Строят проекции контура падающей тени по общим правилам построения тени точки.
Слайд 55Тени архитектурных фрагментов (тени козырьков)
Тень, падающая от козырька прямоугольной формы на
цилиндрическую поверхность строиться по следующему алгоритму:
определяют собственную тень козырька (нижняя и правая боковые грани);
2. для построения собственной тени цилиндрической поверхности на горизонтальной проекции проводят касательную к цилиндру, параллельную проекции светового луча. Через точку касания проводят проекцию образующей.
определяют собственную тень козырька (нижняя и правая боковые грани);
2. для построения собственной тени цилиндрической поверхности на горизонтальной проекции проводят касательную к цилиндру, параллельную проекции светового луча. Через точку касания проводят проекцию образующей.
Слайд 56Тени архитектурных фрагментов (тени козырьков)
3. Проекция падающая тень от прямой ВС
– окружность, радиус которой равен радиусу цилиндра. Для нахождения центра этой окружности из точки В проводят прямую, параллельную фронтальной проекции светового луча до пересечения с осью цилиндра.
4. Тень от линии АВ совпадает с проекцией светового луча, проведенного из точки В₂.
4. Тень от линии АВ совпадает с проекцией светового луча, проведенного из точки В₂.
Слайд 57Тени архитектурных фрагментов (тени козырьков)
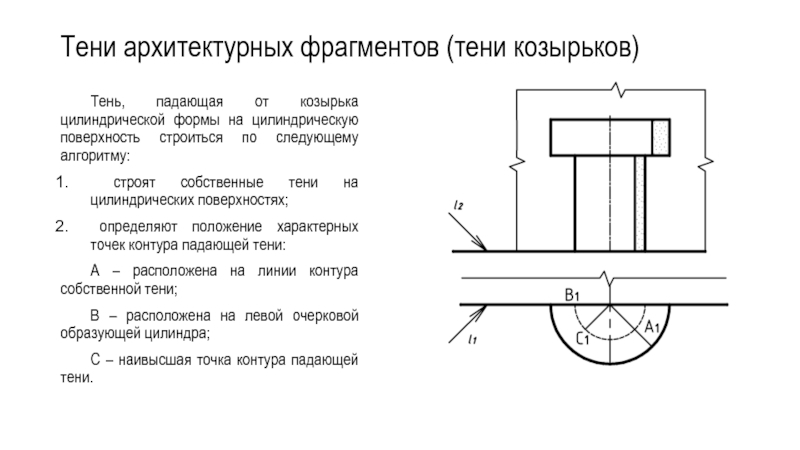
Тень, падающая от козырька цилиндрической формы на
цилиндрическую поверхность строиться по следующему алгоритму:
строят собственные тени на цилиндрических поверхностях;
определяют положение характерных точек контура падающей тени:
А – расположена на линии контура собственной тени;
В – расположена на левой очерковой образующей цилиндра;
С – наивысшая точка контура падающей тени.
строят собственные тени на цилиндрических поверхностях;
определяют положение характерных точек контура падающей тени:
А – расположена на линии контура собственной тени;
В – расположена на левой очерковой образующей цилиндра;
С – наивысшая точка контура падающей тени.
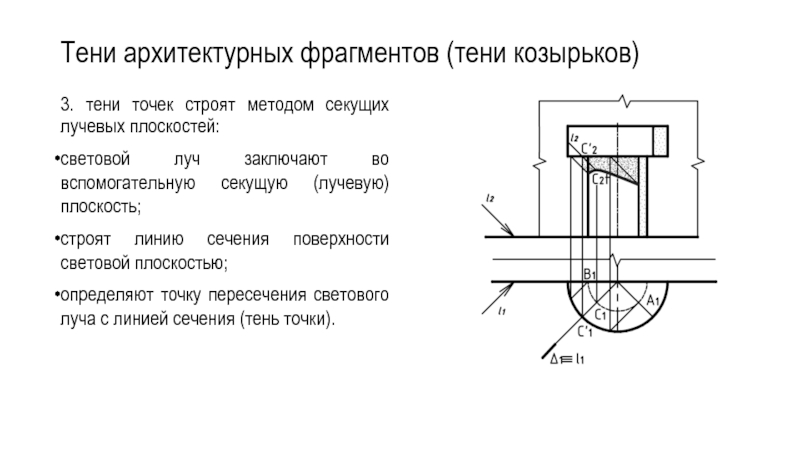
Слайд 58Тени архитектурных фрагментов (тени козырьков)
3. тени точек строят методом секущих лучевых
плоскостей:
световой луч заключают во вспомогательную секущую (лучевую) плоскость;
строят линию сечения поверхности световой плоскостью;
определяют точку пересечения светового луча с линией сечения (тень точки).
световой луч заключают во вспомогательную секущую (лучевую) плоскость;
строят линию сечения поверхности световой плоскостью;
определяют точку пересечения светового луча с линией сечения (тень точки).
Слайд 59Тени архитектурных фрагментов (тени на лестнице)
При построении теней на ступеньках (на
горизонтальных и вертикальных плоскостях) определяют собственную тень объекта и её контур и последовательно строят тени от линий контура собственной тени на параллельные плоскости.
Слайд 60Тени архитектурных фрагментов (тени на ступеньках)
Для построения тени на горизонтальных участках
(проступях) определяют последовательно точки пересечения световых лучей с горизонтальными плоскостями уровня.
Слайд 61Тени архитектурных фрагментов (тени на ступеньках)
Для построения тени на вертикальных участках
(подступенках) определяют последовательно точки пересечения световых лучей с фронтальными плоскостями уровня.