- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Таблицы сопряженности презентация
Содержание
- 1. Таблицы сопряженности
- 2. Цели Вспомнить, что такое таблицы сопряженности Вспомнить, какую статистику можно для них считать
- 3. ТАБЛИЦЫ СОПРЯЖЕННОСТИ Таблицы сопряженности − это
- 4. ТАБЛИЦЫ СОПРЯЖЕННОСТИ В клетке таблицы (на
- 5. Таким образом представленные данные не дают
- 6. Можно их сгруппировать в виде таблиц: по занятости: и по семейному положению:
- 7. А можно и по двум переменным сразу:
- 8. Проценты в таблице сопряженности можно считать тремя
- 9. по строкам, т.е. по зависимой переменной
- 10. по всей таблице сразу:
- 11. ТАБЛИЦЫ СОПРЯЖЕННОСТИ для шкал наименований для шкал порядка
- 12. ТАБЛИЦЫ СОПРЯЖЕННОСТИ для шкал наименований для шкал
- 13. ТАБЛИЦЫ СОПРЯЖЕННОСТИ для шкал наименований для шкал порядка
- 14. СТАТИСТИЧЕСКИЕ КРИТЕРИИ ДЛЯ ТАБЛИЦ СОПРЯЖЕННОСТИ Проверяют,
- 16. χ2 Пирсона Пример: мы хотим проверить, правда
- 17. Было опрошено 550 человек.
- 18. Подсчет критерия χ2 (Пирсона)
- 19. Как определить теоретическую частоту? Для выделенной ячейки:
- 20. Подсчитав таким образом теоретические частоты для всех
- 21. Ограничения критерия χ2 ✵ Наблюдения должны
- 22. χ2 МакНемара (McNemar) Увы! Только для таблиц
- 23. Подсчет критерия χ2 (МакНемара) Ограничения: A+D должно быть не меньше 10!
- 24. Пример: в телестудии проводятся дебаты, нужна ли
- 25. Что делать, если таблица большей размерности, а
- 26. Что делать, если таблица большей размерности, схема
- 27. МЕРЫ ЗАВИСИМОСТИ ДЛЯ ТАБЛИЦ СОПРЯЖЕННОСТИ
- 28. Меры зависимости для шкал наименований Все
- 29. Коэффициент φ ✵ употребляется в
- 30. Коэффициент сопряженности С (или Ф) ✵ разработан
- 31. V Крамера ✵ можно употреблять для
- 32. ТАБЛИЦЫ СОПРЯЖЕННОСТИ для шкал наименований для шкал порядка
- 33. ✵ В таблице сопряженности можно
- 34. Согласованная пара - это пара, где оба
- 35. Несогласованная пара - это пара, где оба
- 36. Связанная пара - это пара, где оба
- 37. Если в таблице преобладают несогласованные пары, то зависимость между переменными отрицательная. 10 20 30
- 38. Если в таблице преобладают согласованные пары, то зависимость между переменными положительная. 10 20 30
- 39. Меры зависимости С- число согласованных пар, D
- 40. ✵ Меры зависимости для шкал порядка имеют
- 41. ☝ STATISTICA не знает, какая шкала была
- 42. Представление данных Посчитать статистику для таблиц сопряженности
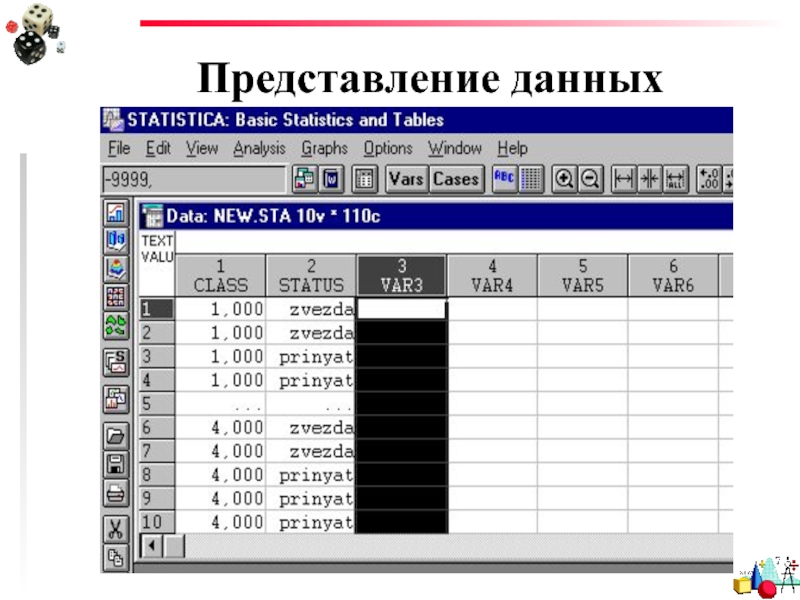
- 43. Представление данных Исходные данные:
- 44. Представление данных
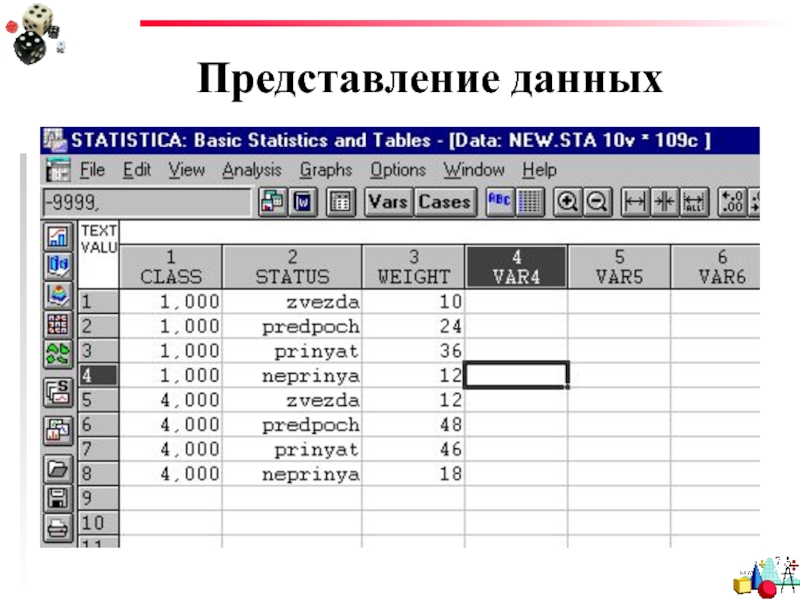
- 45. Представление данных
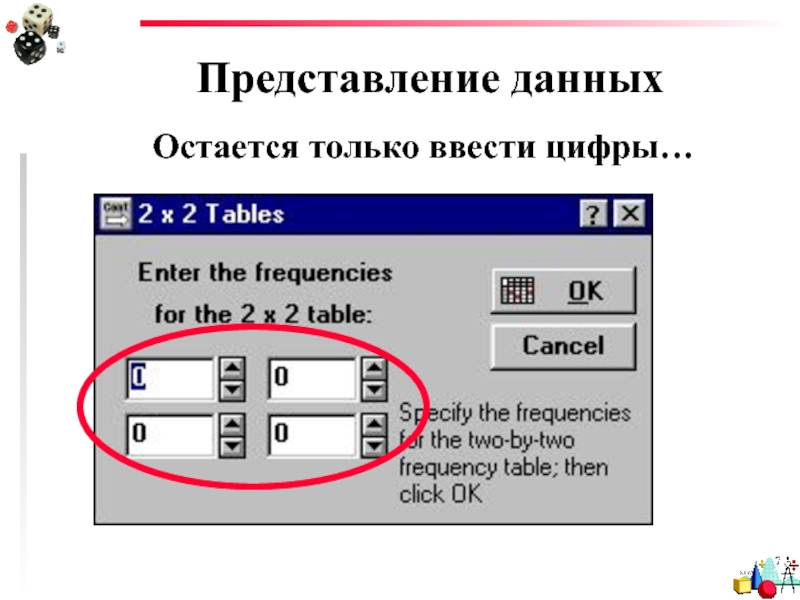
- 46. Представление данных Для таблиц размером 2x2 есть еще модуль в Nonparametrics/Distrib.
- 47. Представление данных Остается только ввести цифры…
- 48. Представление данных И получаем всю статистику!
- 49. Самостоятельная работа К следующему занятию прочитать: Савина
- 50. Можно передохнуть!
Слайд 2Цели
Вспомнить, что такое таблицы сопряженности
Вспомнить, какую статистику можно для них считать
Слайд 3ТАБЛИЦЫ СОПРЯЖЕННОСТИ
Таблицы сопряженности − это совместное распределение двух переменных.
Строки таблицы
образуются значениями одной переменной.
Столбцы таблицы образуются значениями второй переменной.
Столбцы таблицы образуются значениями второй переменной.
Слайд 4ТАБЛИЦЫ СОПРЯЖЕННОСТИ
В клетке таблицы (на пересечении строки и столбца) указывается частота
совместного появления соответствующих значений.
Суммы частот по строке или по столбцу называются маргинальными частотами.
Распределения маргинальных частот представляют собой одномерное распределение переменных.
Суммы частот по строке или по столбцу называются маргинальными частотами.
Распределения маргинальных частот представляют собой одномерное распределение переменных.
Слайд 5Таким образом представленные данные
не дают нам много информации.
Проводим исследование:
X –
семейное положение – НП
Y – занятость - ЗП
Собранные данные выглядят примерно так:
Слайд 7А можно и по двум переменным сразу:
Эта замечательная таблица и называется
таблицей сопряженности
По столбцам обычно приводится независимая переменная
По строкам обычно идет зависимая переменная
Слайд 8Проценты в таблице сопряженности можно считать тремя способами:
по столбцам, т.е.
по независимой переменной
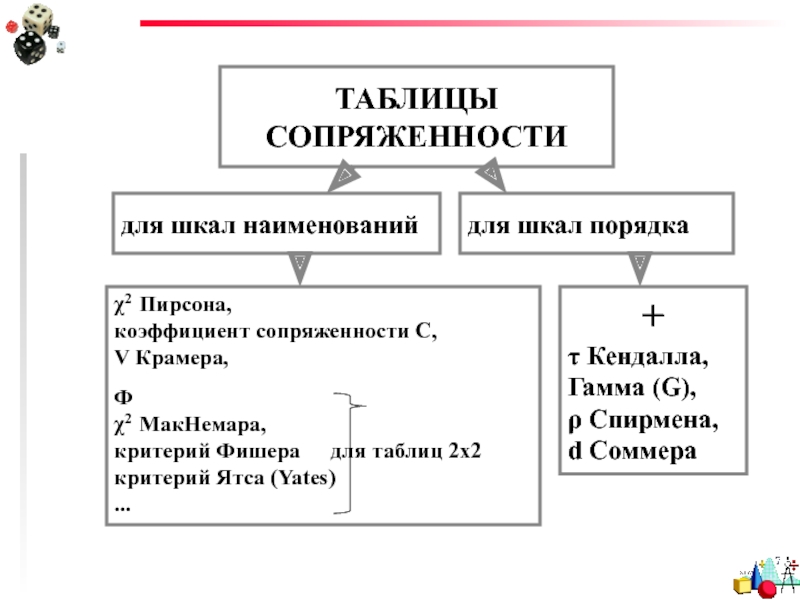
Слайд 12ТАБЛИЦЫ СОПРЯЖЕННОСТИ
для шкал наименований
для шкал порядка
χ2 Пирсона,
коэффициент сопряженности С,
V
Крамера,
Ф
χ2 МакНемара,
критерий Фишера для таблиц 2х2
критерий Ятса (Yates)
...
Ф
χ2 МакНемара,
критерий Фишера для таблиц 2х2
критерий Ятса (Yates)
...
+
τ Кендалла,
Гамма (G),
ρ Спирмена,
d Соммера
Слайд 14СТАТИСТИЧЕСКИЕ КРИТЕРИИ
ДЛЯ ТАБЛИЦ СОПРЯЖЕННОСТИ
Проверяют, есть ли зависимость в распределении одной
переменной от распределения по другой переменной.
Слайд 16χ2 Пирсона
Пример: мы хотим проверить, правда ли,
что мужчины больше любят собак,
а женщины - кошек
а женщины - кошек
Слайд 17 Было опрошено 550 человек. Результаты опроса
представлены в таблице:
Мы можем проверить, зависит ли предпочтение домашнего животного (распределение по переменной Y) от пола
Слайд 18Подсчет критерия χ2
(Пирсона)
- эмпирическая частота,
- теоретическая частота,
k=r*c,
r- число строк в таблице,
c –число столбцов в таблице,
df=(r-1)(c-1).
k=r*c,
r- число строк в таблице,
c –число столбцов в таблице,
df=(r-1)(c-1).
Слайд 19Как определить теоретическую частоту?
Для выделенной ячейки:
Вероятность оказаться мужчиной равна 200/550.
Вероятность предпочитать
собак равна 350/550.
Следовательно, вероятность быть мужчиной и предпочитать собак равна
(200/550 )*(350/550).
Умножив все это на количество испытуемых (550), получим теоретическую частоту для выделенной клетки:
(200/550 )*(350/550)*550=127,3.
Слайд 20Подсчитав таким образом теоретические частоты для всех клеток, находим
χ2=0,18; р=0,67
Следовательно, предпочтение
домашнего животного не зависит от пола: мужчины и женщины одинаково любят собак.
Слайд 21Ограничения критерия χ2
✵ Наблюдения должны быть
независимы.
Поэтому нельзя
использовать одного и того
же испытуемого несколько
раз.
использовать одного и того
же испытуемого несколько
раз.
✵ χ2 пропорционален размеру
выборки. Если увеличить
размер выборки в 2 раза, то и
значение χ2 возрастет в 2 раза.
Поэтому не рекомендуется
применять χ2 для больших
выборок.
✵ Если теоретическая частота
клеток маленькая, то
вычисления могут быть не
точны. Сейчас общепринятым
является правило, что когда
df>1 теоретическая частота
должна быть равна или больше
5 по крайней мере в 80%
клеток.
Слайд 22χ2 МакНемара (McNemar)
Увы! Только для таблиц 2*2.
Тот критерий применяется, чтобы определить,
произошли ли изменения после какого-либо условия. Данные обычно представляются в виде таблицы:
Получается, что A+D – это число изменений
Слайд 24Пример: в телестудии проводятся дебаты, нужна ли смертная казнь. Зрители, сидящие
в зале, опрашиваются до начала дебатов и в конце передачи.
χ2=1,25; p=0,26. Следовательно, можно сделать вывод, что приглашенные ораторы были одинаково успешны в отстаивании своих точек зрения: мнения зрителей существенно не изменились
Слайд 25Что делать, если таблица большей размерности, а схема – интраиндивидуальная?
Для случая,
когда условий больше (до дебатов, после дебатов, через год после дебатов…), можно использовать
Q-критерий Кочрена (Кохрена),
но только если данные представлены как дихотомические переменные
(да/нет, за/против,…)
Q-критерий Кочрена (Кохрена),
но только если данные представлены как дихотомические переменные
(да/нет, за/против,…)
Слайд 26Что делать, если таблица большей размерности, схема – интраиндивидуальная, а данные
не дихотомические?
Не проводить такие исследования!
Слайд 28Меры зависимости
для шкал наименований
Все эти меры не имеют знака и
не показывают направление отношений.
В программе STATISTICA можно посчитать три таких меры
Слайд 29Коэффициент φ
✵ употребляется в основном с
таблицами 2х2
✵ меняется от 0 (когда переменные
независимы) до 1 (когда они
абсолютно зависимы)
✵ меняется от 0 (когда переменные
независимы) до 1 (когда они
абсолютно зависимы)
Слайд 30Коэффициент сопряженности С (или Ф)
✵ разработан для использования с квадратными
таблицами размера больше, чем 2х2
✵ меняется от 0 (когда переменные независимы)
до , где k - число строк (столбцов)
✵ меняется от 0 (когда переменные независимы)
до , где k - число строк (столбцов)
Слайд 31V Крамера
✵ можно употреблять для любых таблиц -
квадратных и прямоугольных
✵ меняется от 0 (когда переменные
независимы) до 1 (когда они абсолютно
зависимы)
✵ меняется от 0 (когда переменные
независимы) до 1 (когда они абсолютно
зависимы)
где c – число строк,
r – число столбцов таблицы.
Слайд 33✵ В таблице сопряженности можно
представлять и
порядковые данные.
✵ Обычно они перечисляются слева направо
(от меньшего к большему) и сверху вниз (от
большего к меньшему):
✵ Обычно они перечисляются слева направо
(от меньшего к большему) и сверху вниз (от
большего к меньшему):
Слайд 34Согласованная пара - это пара, где оба члена ранжированы в одном
порядке по двум направлениям.
B
D
Слайд 35Несогласованная пара - это пара, где оба члена ранжированы в противо-положном
порядке по двум направлениям.
B
А
Слайд 36Связанная пара - это пара, где оба члена ранжированы одинаково по
крайней мере по одному направлению.
C
D
Слайд 37Если в таблице преобладают несогласованные пары, то зависимость между переменными отрицательная.
10
20
30
Слайд 38Если в таблице преобладают согласованные пары, то зависимость между переменными положительная.
10
20
30
Слайд 39Меры зависимости
С- число согласованных пар,
D - число несогласованных пар,
Tx - число
пар, связанных по Х
Ty = число пар, связанных по У
Ty = число пар, связанных по У
Слайд 40✵ Меры зависимости
для шкал порядка имеют знак
✵ τ Кендалла всегда меньше
1, если таблица не квадратная
Слайд 41☝
STATISTICA не знает, какая шкала была использована: определить подходящий критерий или
меру зависимости - полностью ваша проблема
(и ответственность)
(и ответственность)
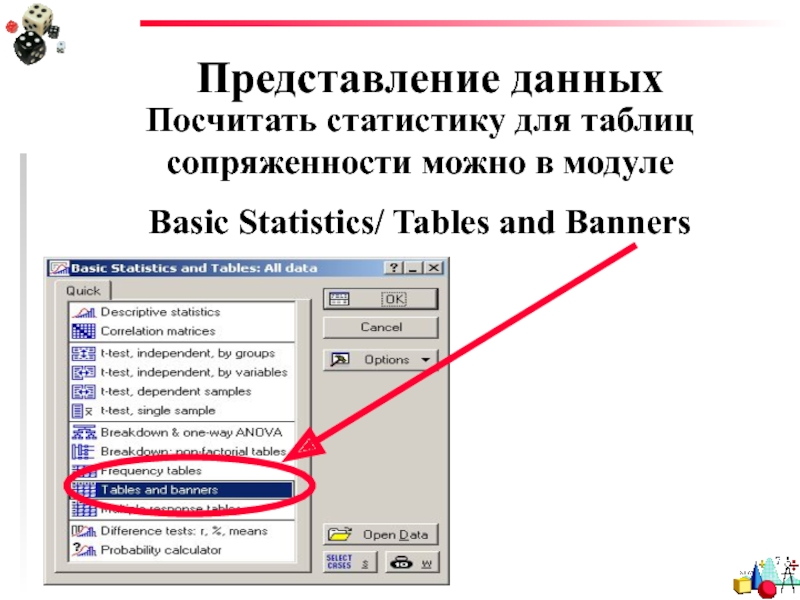
Слайд 42Представление данных
Посчитать статистику для таблиц сопряженности можно в модуле
Basic Statistics/
Tables and Banners
Слайд 49Самостоятельная работа
К следующему занятию прочитать:
Савина и Ванг. Выбор и принятие решений:
риск и социальный контекст// ПЖ, ….
(есть в электронном виде)
(есть в электронном виде)
