- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Свойства определенного интеграла презентация
Содержание
- 1. Свойства определенного интеграла
- 2. Достаточное условие существования определенного интеграла Если
- 3. Свойства определенного интеграла 1 Постоянный множитель можно выносить за знак определенного интеграла.
- 4. Доказательство: Пусть фиксировано разбиение отрезка [a,b] и
- 5. Следовательно по определению:
- 6. 2 Определенный интеграл от алгебраической суммы
- 7. 3 Если отрезок интегрирования разбит на
- 8. Геометрически это означает, что если a
- 9. S S S
- 10. 4 Если на [a,b], где a
- 11. Доказательство: Пусть фиксировано разбиение отрезка [a,b] и
- 12. Следствие. Пусть на [a,b], где a
- 13. Доказательство: По свойству 4 имеем: По свойству 1 и геометрическому смыслу определенного интеграла:
- 14. 5 Если на [a,b], где a
- 15. Доказательство: По свойству функции, непрерывной на отрезке,
- 16. Но функция, непрерывная на отрезке, принимает
- 17. Пусть Тогда теорема о среднем утверждает, что
- 19. Равенство называется формулой среднего значения. называется средним значением функции.
- 20. 6 Если на [a,b] функция y=f(x)
Слайд 1Необходимое условие существования
определенного интеграла
12.2. СВОЙСТВА ОПРЕДЕЛЕННОГО
ИНТЕГРАЛА
Интегрируемая на отрезке [a,b]
y=f(x) ограничена на этом отрезке.
Слайд 2Достаточное условие существования
определенного интеграла
Если на отрезке [a,b] функция y=f(x)
непрерывна,
этом отрезке.
Слайд 3Свойства
определенного интеграла
1
Постоянный множитель можно выносить
за знак определенного интеграла.
Слайд 4Доказательство:
Пусть фиксировано разбиение отрезка [a,b] и выбор точек
Рассмотрим интегральную сумму:
Переходим
Слайд 62
Определенный интеграл от алгебраической
суммы (разности) двух функций равен
сумме (разности)
этих функций.
Слайд 73
Если отрезок интегрирования разбит
на части, то интеграл на всем отрезке
равен сумме интегралов по каждому
из участков разбиения.
Слайд 8Геометрически это означает, что если a
Слайд 11Доказательство:
Пусть фиксировано разбиение отрезка [a,b] и выбор точек
то для интегральных
Если
Переходим к пределу в левой и правой части неравенства при
Слайд 13Доказательство:
По свойству 4 имеем:
По свойству 1 и геометрическому смыслу определенного интеграла:
Слайд 15Доказательство:
По свойству функции, непрерывной на отрезке, для произвольного значения
справедливо неравенство:
Где
Слайд 16
Но функция, непрерывная на отрезке, принимает любое значение, заключенное между ее
что
Слайд 17Пусть
Тогда теорема о среднем утверждает, что найдется такая точка
что площадь под
Слайд 206
Если на [a,b] функция y=f(x) неотрицательна, то площадь под этой кривой
Геометрический смысл
определенного интеграла
![Необходимое условие существования определенного интеграла12.2. СВОЙСТВА ОПРЕДЕЛЕННОГО ИНТЕГРАЛАИнтегрируемая на отрезке [a,b] функция y=f(x) ограничена на](/img/tmb/1/19276/67b1fad65d1623d561be3e911b4e6259-800x.jpg)
![Достаточное условие существования определенного интегралаЕсли на отрезке [a,b] функция y=f(x) непрерывна, то она интегрируема на](/img/tmb/1/19276/237aa15319856fe47e775c0c60dc1139-800x.jpg)

![Доказательство:Пусть фиксировано разбиение отрезка [a,b] и выбор точек Рассмотрим интегральную сумму:Переходим к пределу в левой](/img/tmb/1/19276/7cf2240f236a0454a1745e2a8cf42e0f-800x.jpg)




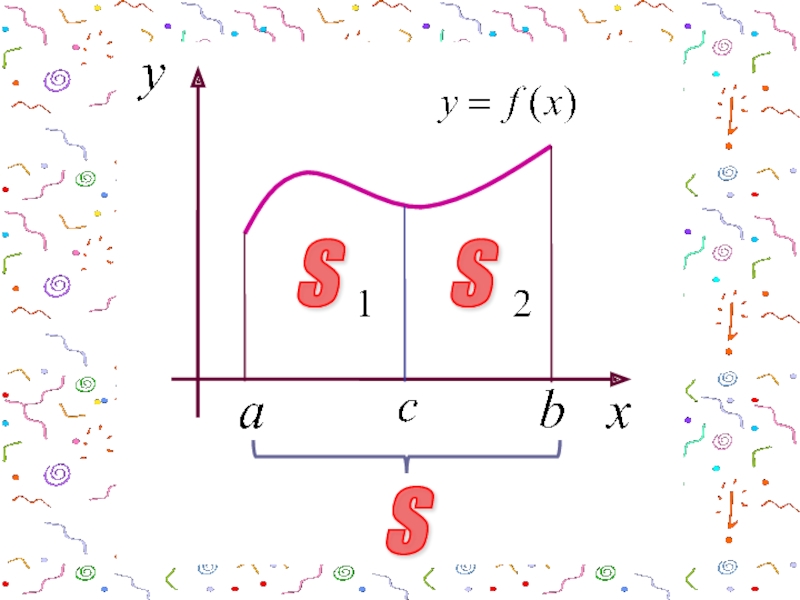
![4Если на [a,b], где a](/img/tmb/1/19276/05c7e699451378a81ece7a307f299314-800x.jpg)
![Доказательство:Пусть фиксировано разбиение отрезка [a,b] и выбор точек то для интегральных сумм:ЕслиПереходим к пределу в](/img/tmb/1/19276/6f8844e999850adc8f701d31653d17f9-800x.jpg)
![Следствие.Пусть на [a,b], где a](/img/tmb/1/19276/f722fad3b6359b31c40e398ce160611c-800x.jpg)

![5Если на [a,b], где a](/img/tmb/1/19276/fab3a7744c66cd69b961f25be8053ead-800x.jpg)


![ПустьТогда теорема о среднем утверждает, что найдется такая точкачто площадь под кривой y=f(x) на [a,b]](/img/tmb/1/19276/36a294687cffb623e84a5d7456722c67-800x.jpg)


![6Если на [a,b] функция y=f(x) неотрицательна, то площадь под этой кривой численно равна определенному интегралуГеометрический](/img/tmb/1/19276/78303157e079958fb4857e1e51898a1f-800x.jpg)