pptcloud.ru
- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Свойства функций у = tgx и y = ctgx и их графики презентация
Содержание
- 1. Свойства функций у = tgx и y = ctgx и их графики
- 2. y = tgx Функция y = tgx
- 3. Построим график на промежутке [0;П/2) и отразим
- 4. При функция у = tgx не определена. Если х
- 5. Построение графика функции у=tg x на всей
- 6. Основные свойства функции y=tgx 1) Область
- 7. 5)Функция принимает значение, равно 0, при
- 8. Задача 1: Найти все корни уравнения
- 9. Задача 2: Найти все решения неравенства tg
- 10. Сравнить числа: tg П/5 и tg П/7
- 11. Свойства функции у=tgx и у=ctgx
- 12. у=ctgx Для построения графика функции у=ctgx воспользуемся
- 13. Основные свойства функции у=ctgx Область определения- множество
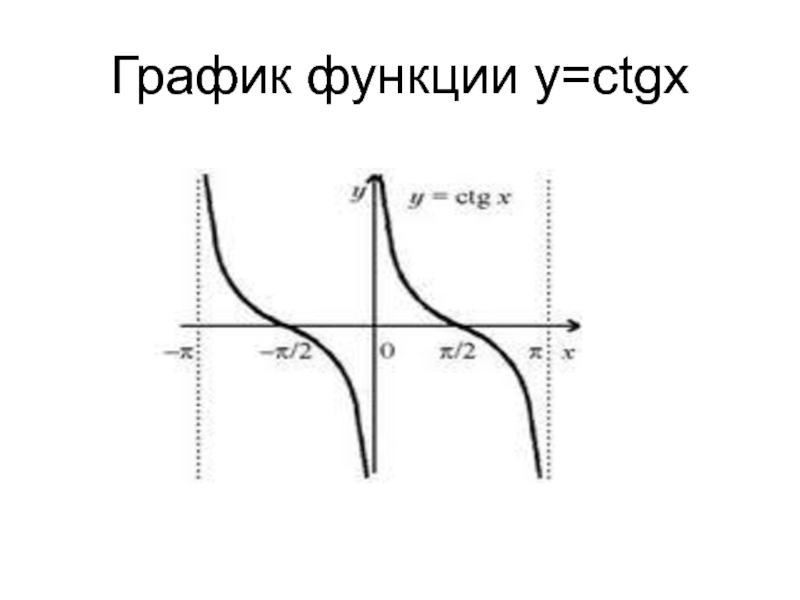
- 14. График функции у=ctgx
Слайд 2y = tgx
Функция y = tgx определена при
, является нечетной и периодической с периодом П.
Покажем, что на промежутке функция y = tgx возратает.
Покажем, что на промежутке функция y = tgx возрастает. Пусть 0≤x1т.е. . По условию 0≤x1свойствам функции у=cos x имеем cos x1> cos x2>0, откуда 0< . Перемножив неравенства sin x1< sin x2
и получим
Покажем, что на промежутке функция y = tgx возратает.
Покажем, что на промежутке функция y = tgx возрастает. Пусть 0≤x1
и получим
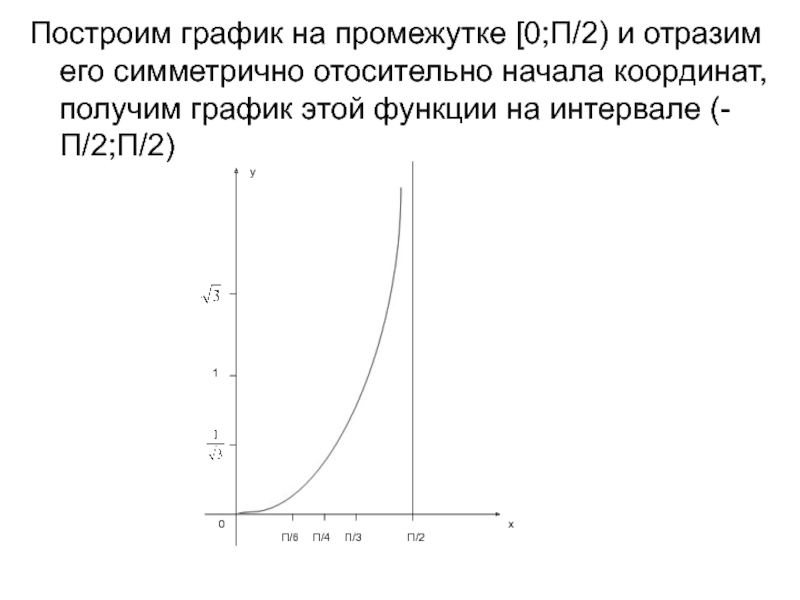
Слайд 3Построим график на промежутке [0;П/2) и отразим его симметрично отосительно начала
координат, получим график этой функции на интервале (-П/2;П/2)
у
х
1
П/6
П/4
П/3
П/2
0
Слайд 4При функция у = tgx не определена.
Если х<П/2 и х приближается к П/2, то sin x приближается к 1, а cos, оставаясь положительным, стремится к нулю. При этом дробь возрастает и поэтому график функции y = tgx приближается к вертикальной прямой х=П/2. Аналогично при отрицательных значениях х, больших - П/2 и приближающихся к - П/2 , график функции y = tgx приближается к вертикальной прямой х=-П/2, т.е. прямые х=П/2 и х=-П/2 являются вертикальными асимптотами графика функции.
Слайд 5Построение графика функции у=tg x на всей бласти определения:
Функция у=tg x
периодичская с периодом П, следовательно график этой функции получается на интрвале от (-П/2;П/2) сдвигами вдоль оси абсцисс на Пk, где
Слайд 6Основные свойства функции y=tgx
1) Область
определения – множество всех действительных чисел
2)Множество значений R всех действительных чисел.
3)Периодическая с периодам
4)Нечетная.
2)Множество значений R всех действительных чисел.
3)Периодическая с периодам
4)Нечетная.
Слайд 75)Функция принимает значение, равно 0, при
Положительные значения на интервале
Отрицательные
Возрастающая
Слайд 8Задача 1: Найти все корни уравнения
tg x=2 принадлежащие отрезку [-П;3П/2]
Построим
графики функций у=2 и у= tg x. Эти графики пересекаются в 3-х точках, абсциссы которых х1, х2, х3 являются корнями уравнения tg x=2. На интервале (-П/2;П/2) уравнение имеет корень х1=arctg2. т.к. функция у=tg х периодическая с периодом П, то х2= arctg2 + П, х3= arctg2 – П.
Ответ: х1=arctg2, х2= arctg2 + П, х3= arctg2 – П.
Ответ: х1=arctg2, х2= arctg2 + П, х3= arctg2 – П.
Слайд 9Задача 2: Найти все решения неравенства tg x≤2, принадлежащие отрезку [-П;3П/2]
Построим
графики функций у=2 и у= tg x. Из графика видно, что график функции у=tg х лежит не выше прямой у=2 на промежутках [-П;х3], (-П/2;х1] и (П/2;х2].
Ответ: [-П;-П+ arctg2], (-П/2; arctg2], (П/2; П+ arctg2]
Ответ: [-П;-П+ arctg2], (-П/2; arctg2], (П/2; П+ arctg2]
Слайд 10Сравнить числа:
tg П/5 и tg П/7
tg П/5 > tg П/7
tg
7П/8 и tg 8П/9
tg 7П/8 < tg 8П/9
tg 7П/8 < tg 8П/9
tg (-7П/8) и tg (-8П/9)
tg (-7П/8) > tg (-8П/9)
tg (-П/5) и tg (-П/7)
tg (-П/5) > tg (-П/7)
tg 2 и tg 3
tg 2 < tg 3
tg 1 и tg 1,5
tg 1 < tg 1,5
Слайд 12у=ctgx
Для построения графика функции у=ctgx воспользуемся тождеством ctgx=-tg(x+п/2).Из этого тождества следует,
что для построения графика ctg необходимо сдвинуть график tg на п/2 влево вдоль оси 0x и отразить полученную кривую относительно оси 0х.Графики tg и ctg состоят из бесконечного множества одинаковых периодически повторяющихся ветвей.
Слайд 13Основные свойства функции у=ctgx
Область определения- множество всех действительных чисел
Множество значений-
множество R всех действительных чисел
Функция у=ctgx периодическая с периодом Т=П
Функция у=ctgx нечетная
Функция у=ctgx принимает значения, равные нулю при
-положительные значения на интервалах
-отрицательные значения на интервалах
Функция у=ctgx является убывающей на каждом интервале
Функция у=ctgx периодическая с периодом Т=П
Функция у=ctgx нечетная
Функция у=ctgx принимает значения, равные нулю при
-положительные значения на интервалах
-отрицательные значения на интервалах
Функция у=ctgx является убывающей на каждом интервале






![Задача 1: Найти все корни уравнения tg x=2 принадлежащие отрезку [-П;3П/2]Построим графики функций у=2 и](/img/tmb/3/265633/c112709345161d5c6d60c058624c0e7b-800x.jpg)
![Задача 2: Найти все решения неравенства tg x≤2, принадлежащие отрезку [-П;3П/2]Построим графики функций у=2 и](/img/tmb/3/265633/710990be018bd0c8f4b2a2f17c6ad681-800x.jpg)