- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Структурные средние. Мода, медиана презентация
Содержание
- 1. Структурные средние. Мода, медиана
- 2. СТРУКТУРНЫЕ СРЕДНИЕ: - МОДА - МЕДИАНА
- 3. Значимость описательных средних величин Мода,
- 4. МОДА - Мо чаще всего встречающаяся варианта,
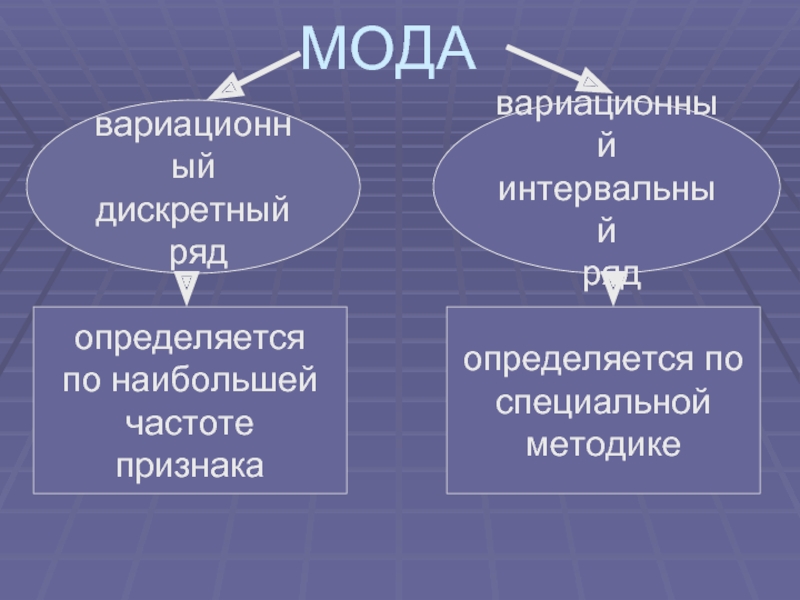
- 5. МОДА вариационный дискретный ряд вариационный
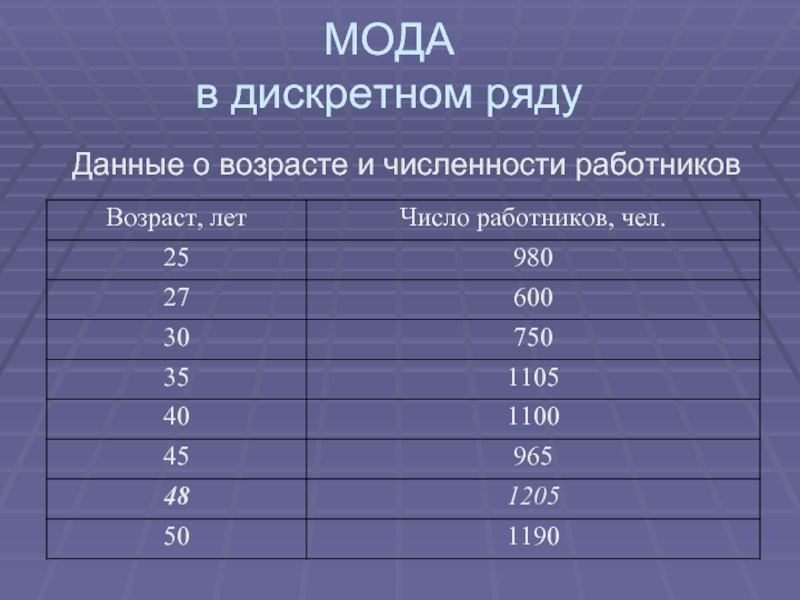
- 6. МОДА в дискретном ряду Данные о возрасте и численности работников
- 7. МОДА в интервальном ряду Определяется модальный
- 8. Расчет моды в интервальном ряду
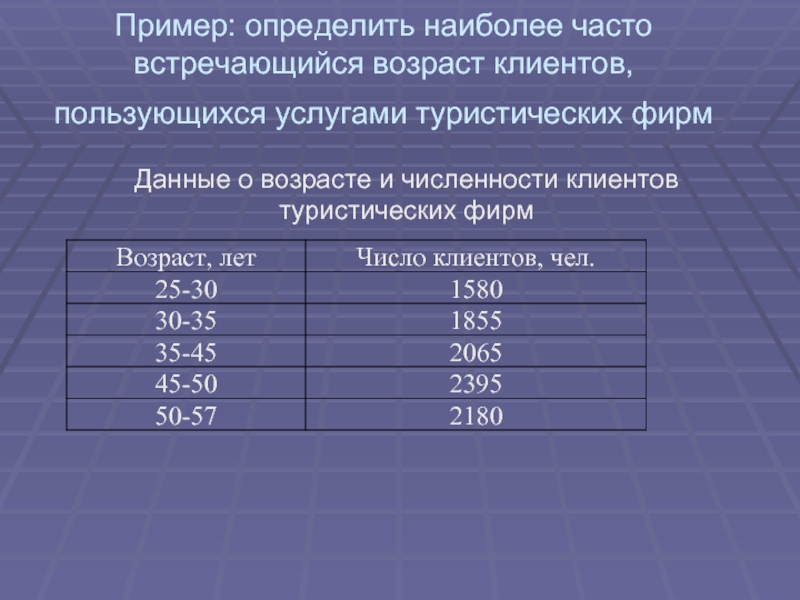
- 9. Пример: определить наиболее часто встречающийся возраст клиентов,
- 10. Мо = 45+5*
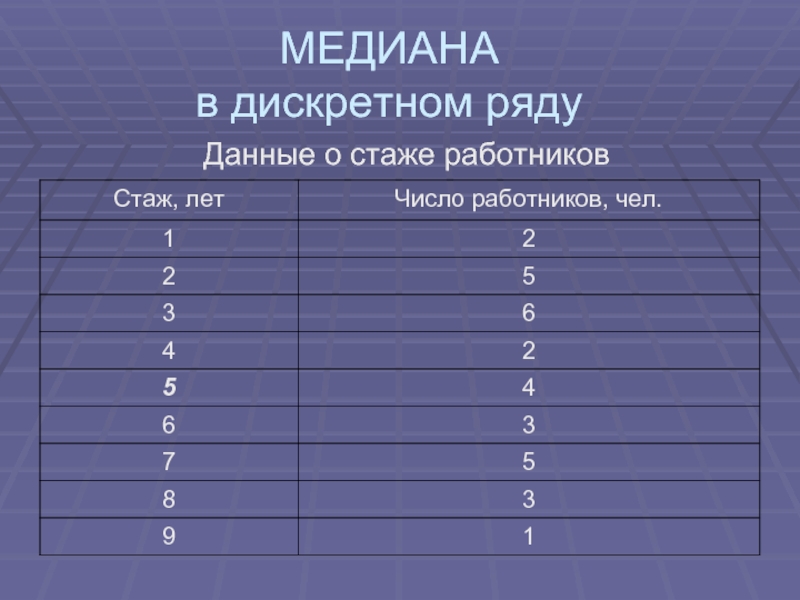
- 11. Медиана (Ме) значение признака, находящегося в середине
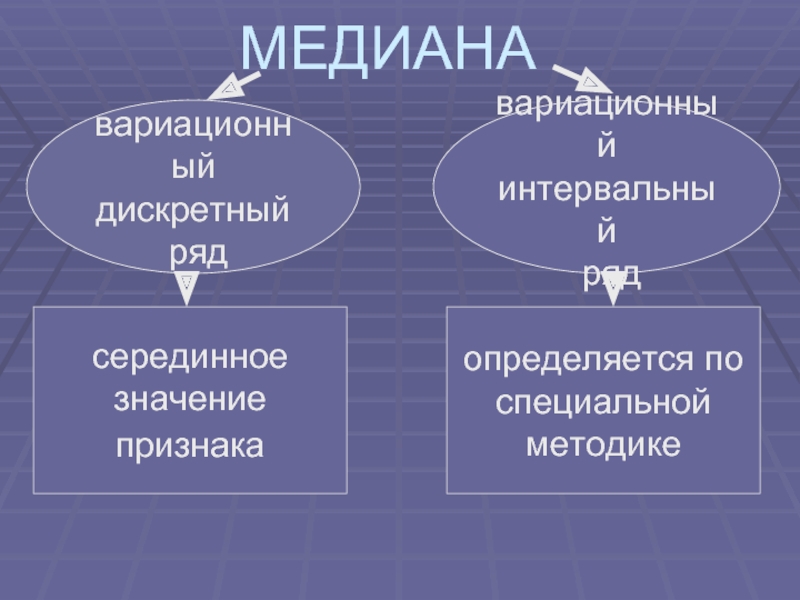
- 12. МЕДИАНА вариационный дискретный ряд вариационный
- 13. МЕДИАНА в дискретном ряду Данные о стаже работников
- 14. МЕДИАНА в интервальном ряду Определяется медианный
- 15. Расчет медианы в интервальном ряду
- 16. Пример: определить значение медианы по интервальному ряду распределения, характеризующему стаж работников Данные о стаже работников
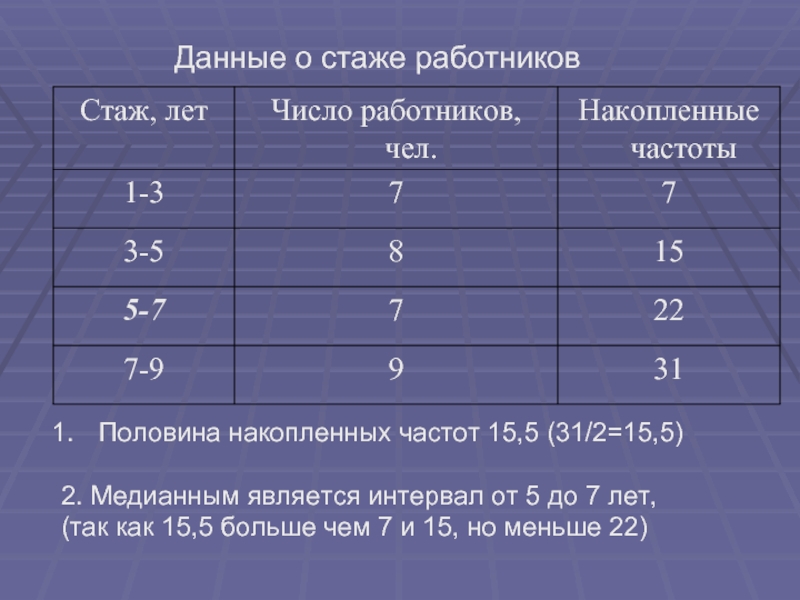
- 17. Данные о стаже работников Половина накопленных
- 18. Ме=5+2* 15,5-15 = 5,1 года 7 по
- 19. характеристика распределения признаков в совокупности
СТРУКТУРНЫЕ СРЕДНИЕ:
- МОДА - МЕДИАНА
Слайд 3Значимость описательных средних величин
Мода, медиана
позволяют изучить
внутреннее
строение рядов
распределения
Слайд 4МОДА - Мо
чаще всего встречающаяся варианта, значение признака, которое соответствует максимальной
частоте в ряду распределения. Мода отражает наиболее типичный признак.
Для вариационного ряда с не сгруппированным данным моды не существует.
Для вариационного ряда с не сгруппированным данным моды не существует.
Слайд 5МОДА
вариационный
дискретный
ряд
вариационный
интервальный
ряд
определяется
по наибольшей
частоте
признака
определяется по
специальной
методике
Слайд 7МОДА
в интервальном ряду
Определяется модальный интервал – по наибольшей частоте
Рассчитывается значение
моды по формуле
Слайд 8Расчет моды в интервальном ряду
-начало модального интервала
-длина модального
интервала
-частота модального интервала
-частота интервала, предшествующего модальному
-частота интервала, следующего за модальным
Слайд 9Пример: определить наиболее часто встречающийся возраст клиентов, пользующихся услугами туристических фирм
Данные о возрасте и численности клиентов туристических фирм
Слайд 10Мо = 45+5* 2395-2065
(2395-2065)+(2395-2180)
Чаще всего в туристические фирмы обращаются клиенты, возраст которых составляет около 48 лет
= 48,03
Слайд 11Медиана (Ме)
значение признака, находящегося в середине ряда распределения.
Медиана делит вариационный
ряд на две равные части: одна часть имеет значения варьирующего признака меньшие, чем медиана, другая - большие.
Слайд 12МЕДИАНА
вариационный
дискретный
ряд
вариационный
интервальный
ряд
серединное
значение
признака
определяется по
специальной
методике
Слайд 14МЕДИАНА
в интервальном ряду
Определяется медианный интервал – по накопленным (кумулятивным) частотам
Рассчитывается
значение медианы по формуле
Слайд 15Расчет медианы в интервальном ряду
- начало медианного интервала
- длина модального интервала
- кумулятивная частота интервала, предшествующего
медианному
- частота медианного интервала (не накопленная)
Слайд 16Пример: определить значение медианы по интервальному ряду распределения, характеризующему стаж работников
Данные
о стаже работников
Слайд 17Данные о стаже работников
Половина накопленных частот 15,5 (31/2=15,5)
2. Медианным
является интервал от 5 до 7 лет,
(так как 15,5 больше чем 7 и 15, но меньше 22)
(так как 15,5 больше чем 7 и 15, но меньше 22)
Слайд 18Ме=5+2* 15,5-15 = 5,1 года
7
по данному ряду распределения половина работников
имеет
стаж менее 5,1 года,
половина более 5,1 года
половина более 5,1 года
Слайд 19характеристика распределения признаков в совокупности
Мо=Ме=
совокупность считается
абсолютно симметричной
Мо
правосторонняя
ассиметрия в совокупности
ассиметрия в совокупности
Мо>Ме>
имеется левосторонняя
ассиметрия в совокупности
