Stolz-Cesaro Theorem презентация

Содержание

1. Stolz-Cesaro Theorem
2. Question 4. Find the limit of the
3. Stolz-Cesaro Theorem Let an and bn be
4. Thus, the Stolz-Cesaro Theorem tells us that
5. apply the Stolz-Cesaro Theorem to or
6. Question 0: Answers to Questions from Light
7. Calculus++ Also known as Hysterical Calculus
8. Question 1a. Find the following limit Solution.
9. The Stolz-Cesaro Theorem tells us that Hence
10. Cauchy Criterion A sequence xn, n =
11. Definition (of non-fundamental sequences). A sequence xn,
12. Question 3. The sequence –1, +1, –1,
13. Question 4. Use the Cauchy criterion to
14. Therefore, our sequence {xn} is not fundamental,
15. Question 5. Use the Cauchy criterion to
16. Thus we set Therefore Thus, the sequence
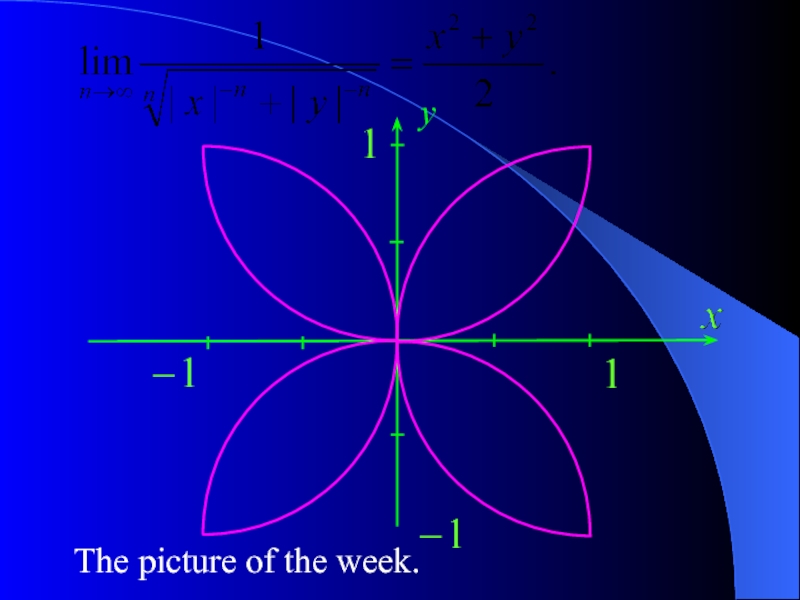
17. Picture of the Week
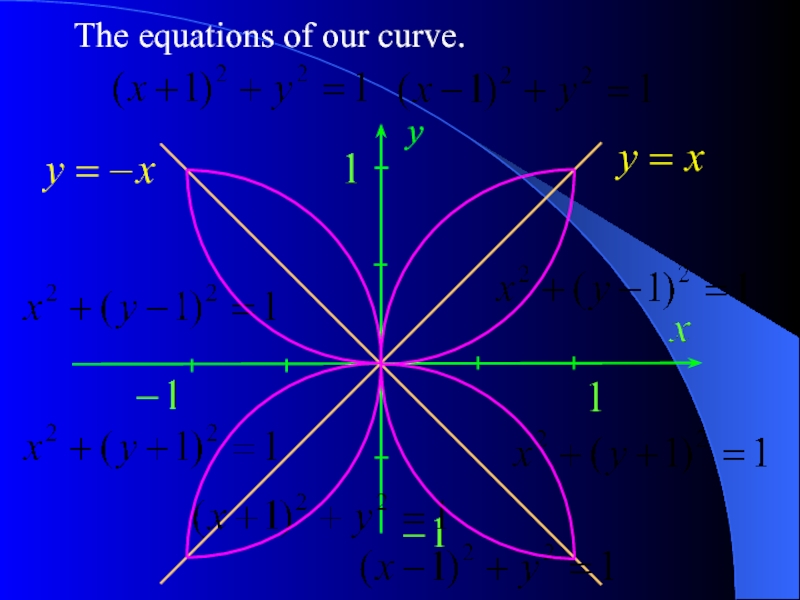
18. Question 8. Draw the curve defined by the Solution. We already know that Therefore equation
19. Thus, we have to draw the curve defined by the equation
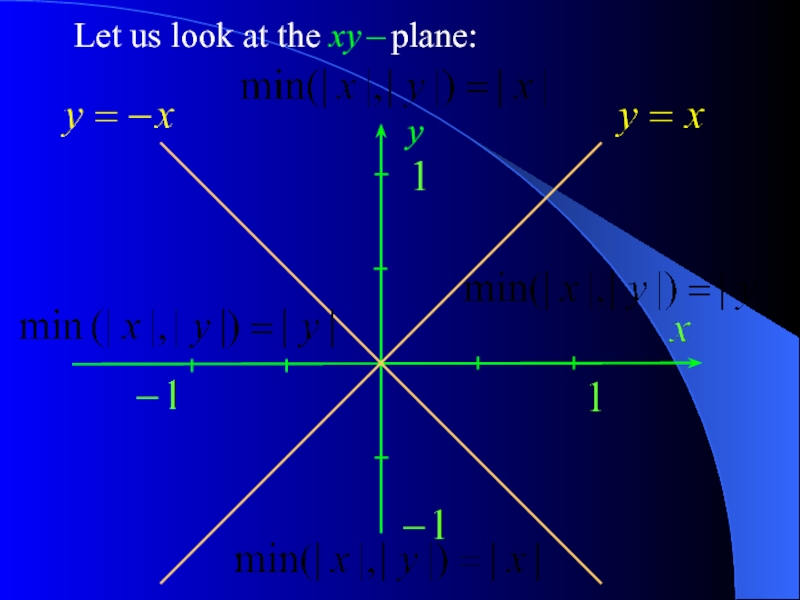
20. Let us look at the xy – plane: y
21. The curve defined by the equation is
22. The equations of our curve. y
23. The picture of the week. y
24. Question 2: Answers to Questions from Seminar

Question 4. Find the limit of the sequence Solution. Our sequence can be written down as follows Therefore the nth term of the sequence is given by Using the formula

Слайд 1Calculus++ Light
Sudoku no more!

Слайд 2Question 4. Find the limit of the sequence
Solution. Our sequence can

be written down as follows

Therefore the nth term of the sequence is given by

Using the formula for the sum of a geometric series we obtain

Слайд 3Stolz-Cesaro Theorem
Let an and bn be two sequences of real numbers.
Assume

that:

is increasing for sufficiently large n,

Then

Question 1.

Solution. The conditions I and II of the Stolz-Cesaro theorem are satisfied.

Слайд 4 Thus, the Stolz-Cesaro Theorem tells us that
To find the limit
either

apply the Stolz-Cesaro Theorem twice,

Слайд 5 apply the Stolz-Cesaro Theorem to
or write it down as a

product

and then use the product rule

Слайд 6 Question 0:
Answers to Questions from Light #1:
Sequences and Limits
Question 1:
Question

Question 5:

Question 2:

Слайд 7Calculus++
Also known as Hysterical Calculus

Слайд 8Question 1a. Find the following limit
Solution. Use the Stolz-Cesaro theorem.
In this

case

The sequence bn is infinitely large and increasing. Hence, the conditions I and II of the Stolz-Cesaro theorem are satisfied.

Слайд 9The Stolz-Cesaro Theorem tells us that

Hence

Слайд 10Cauchy Criterion
A sequence xn, n = 1,2,3,… is called a fundamental

sequence (or Cauchy sequence) if for any we can find a number N such that, for any n > N and any m > 0:

Theorem (Cauchy Criterion). A sequence xn, n = 1,2,3,…, converges if and only if it is a Cauchy sequence.

Слайд 11Definition (of non-fundamental sequences).
A sequence xn, n = 1,2,3,… is not

a Cauchy sequence if we can find such that, for any number N, we can find n > N and m > 0, such that

Слайд 12Question 3. The sequence –1, +1, –1, +1,… is not a

Cauchy sequence (and, hence, it diverges).
Solution. Let and let N be any natural number. Take n = 2N + 1, m = 1.
Since n is odd and n + m is even, we have xn= –1 and xn+m = +1.
Hence

Therefore, the sequence
{xn} = –1, +1, –1, +1, …
is not a Cauchy sequence.

Слайд 13Question 4. Use the Cauchy criterion to show that the sequence

diverges.
Solution: According to the Cauchy criterion it is sufficient to show that {xn} is not a fundamental sequence:

We have

Слайд 14Therefore, our sequence {xn} is not fundamental, and the Cauchy criterion

tells us that {xn} diverges.

Choosing m = n we obtain

Thus,

(for instance, ),

(we set m = n):

Слайд 15Question 5. Use the Cauchy criterion to show
converges.
Solution: It is sufficient

to show that the sequence xn is fundamental:

We have

that the sequence

Слайд 16Thus
we set
Therefore
Thus, the sequence xn is fundamental, and therefore it converges

to some limit L.

In fact,

Слайд 17Picture of the Week

Слайд 18Question 8. Draw the curve defined by the
Solution. We already know

that

Therefore

equation

Слайд 19Thus, we have to draw the curve defined by the equation

Слайд 20Let us look at the xy – plane:
y

Слайд 21The curve defined by the equation
is the circle with the radius

1, centred at the point (0,1).
Indeed,

The curve defined by the equation

is the circle with the radius 1, centred at the point (1,0):

Слайд 22The equations of our curve.
y

Слайд 23The picture of the week.
y

Слайд 24 Question 2:
Answers to Questions from Seminar 1.
Question 8b:
Question 8c:
Question 9:
Question 3:

Скачать презентацию

Stolz-Cesaro Theorem презентация

Содержание

Слайд 1Calculus++ Light
Sudoku no more!

Слайд 2Question 4. Find the limit of the sequence
Solution. Our sequence can

Слайд 3Stolz-Cesaro Theorem
Let an and bn be two sequences of real numbers.
Assume

Слайд 4 Thus, the Stolz-Cesaro Theorem tells us that
To find the limit
either

Слайд 5 apply the Stolz-Cesaro Theorem to
or write it down as a

Слайд 6 Question 0:
Answers to Questions from Light #1:
Sequences and Limits
Question 1:
Question

Слайд 7Calculus++
Also known as Hysterical Calculus

Слайд 8Question 1a. Find the following limit
Solution. Use the Stolz-Cesaro theorem.
In this

Слайд 9The Stolz-Cesaro Theorem tells us that

Hence

Слайд 10Cauchy Criterion
A sequence xn, n = 1,2,3,… is called a fundamental

Слайд 11Definition (of non-fundamental sequences).
A sequence xn, n = 1,2,3,… is not

Слайд 12Question 3. The sequence –1, +1, –1, +1,… is not a

Слайд 13Question 4. Use the Cauchy criterion to show that the sequence

Слайд 14Therefore, our sequence {xn} is not fundamental, and the Cauchy criterion

Слайд 15Question 5. Use the Cauchy criterion to show
converges.
Solution: It is sufficient

Слайд 16Thus
we set
Therefore
Thus, the sequence xn is fundamental, and therefore it converges

Слайд 17Picture of the Week

Слайд 18Question 8. Draw the curve defined by the
Solution. We already know

Слайд 19Thus, we have to draw the curve defined by the equation

Слайд 20Let us look at the xy – plane:
y

Слайд 21The curve defined by the equation
is the circle with the radius

Слайд 22The equations of our curve.
y

Слайд 23The picture of the week.
y

Слайд 24 Question 2:
Answers to Questions from Seminar 1.
Question 8b:
Question 8c:
Question 9:
Question 3:

Обратная связь

Что такое ThePresentation.ru?

Stolz-Cesaro Theorem презентация

Содержание

Слайд 1Calculus++ LightSudoku no more!

Слайд 2Question 4. Find the limit of the sequenceSolution. Our sequence can

Слайд 3Stolz-Cesaro TheoremLet an and bn be two sequences of real numbers.Assume

Слайд 4 Thus, the Stolz-Cesaro Theorem tells us that To find the limit either

Слайд 5 apply the Stolz-Cesaro Theorem to or write it down as a

Слайд 6 Question 0: Answers to Questions from Light #1: Sequences and Limits Question 1: Question

Слайд 7Calculus++Also known as Hysterical Calculus

Слайд 8Question 1a. Find the following limitSolution. Use the Stolz-Cesaro theorem.In this

Слайд 9The Stolz-Cesaro Theorem tells us that Hence

Слайд 10Cauchy CriterionA sequence xn, n = 1,2,3,… is called a fundamental

Слайд 11Definition (of non-fundamental sequences).A sequence xn, n = 1,2,3,… is not

Слайд 12Question 3. The sequence –1, +1, –1, +1,… is not a

Слайд 13Question 4. Use the Cauchy criterion to show that the sequence

Слайд 14Therefore, our sequence {xn} is not fundamental, and the Cauchy criterion

Слайд 15Question 5. Use the Cauchy criterion to show converges.Solution: It is sufficient

Слайд 16Thus we setThereforeThus, the sequence xn is fundamental, and therefore it converges

Слайд 17Picture of the Week

Слайд 18Question 8. Draw the curve defined by theSolution. We already know

Слайд 19Thus, we have to draw the curve defined by the equation

Слайд 20Let us look at the xy – plane:y

Слайд 21The curve defined by the equation is the circle with the radius

Слайд 22The equations of our curve.y

Слайд 23The picture of the week.y

Слайд 24 Question 2: Answers to Questions from Seminar 1. Question 8b: Question 8c: Question 9: Question 3:

Похожие презентации

Обратная связь

Что такое ThePresentation.ru?

Слайд 1Calculus++ Light
Sudoku no more!

Слайд 2Question 4. Find the limit of the sequence
Solution. Our sequence can

Слайд 3Stolz-Cesaro Theorem
Let an and bn be two sequences of real numbers.
Assume

Слайд 4 Thus, the Stolz-Cesaro Theorem tells us that
To find the limit
either

Слайд 5 apply the Stolz-Cesaro Theorem to
or write it down as a

Слайд 6 Question 0:
Answers to Questions from Light #1:
Sequences and Limits
Question 1:
Question

Слайд 7Calculus++
Also known as Hysterical Calculus

Слайд 8Question 1a. Find the following limit
Solution. Use the Stolz-Cesaro theorem.
In this

Слайд 9The Stolz-Cesaro Theorem tells us that

Hence

Слайд 10Cauchy Criterion
A sequence xn, n = 1,2,3,… is called a fundamental

Слайд 11Definition (of non-fundamental sequences).
A sequence xn, n = 1,2,3,… is not

Слайд 15Question 5. Use the Cauchy criterion to show
converges.
Solution: It is sufficient

Слайд 16Thus
we set
Therefore
Thus, the sequence xn is fundamental, and therefore it converges

Слайд 18Question 8. Draw the curve defined by the
Solution. We already know

Слайд 20Let us look at the xy – plane:
y

Слайд 21The curve defined by the equation
is the circle with the radius

Слайд 22The equations of our curve.
y

Слайд 23The picture of the week.
y

Слайд 24 Question 2:
Answers to Questions from Seminar 1.
Question 8b:
Question 8c:
Question 9:
Question 3: