- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Степенные ряды презентация
Содержание
- 1. Степенные ряды
- 2. 14.1. ОБЛАСТЬ СХОДИМОСТИ СТЕПЕННОГО РЯДА Рассмотрим
- 3. Степенным называется ряд 1 Числа С0…Сn называются коэффициентами степенного ряда.
- 4. При разных значениях х будут получаться разные
- 5. Частичная сумма степенного ряда будет функцией
- 6. ПРИМЕР. Найти область сходимости степенного ряда
- 7. РЕШЕНИЕ. Данный ряд можно рассматривать как геометрический
- 8. ТЕОРЕМА АБЕЛЯ 1 Если степенной ряд
- 9. 2 Если степенной ряд расходится при
- 10. ДОКАЗАТЕЛЬСТВО: По условию ряд (1) сходится при Следовательно выполняется необходимый признак сходимости: Поэтому последовательность 1
- 11. Рассмотрим ряд, состоящий из абсолютных величин ряда
- 12. который можно рассматривать как сходящийся геометрический ряд
- 13. 2 По условию ряд (1) расходится при
- 14. Из теоремы Абеля следует, что существует такое
- 15. Если степенной ряд сходится не только
- 16. ДОКАЗАТЕЛЬСТВО: Пусть Х – множество точек х,
- 17. Если не существует такой точки х1, где
- 18. Пусть теперь х – любе число, удовлетворяющее
- 19. Число R называется радиусом сходимости, а интервал
- 20. Коэффициенты этого ряда, по крайней мере, начиная
- 21. Радиус сходимости степенного ряда
- 22. ПРИМЕР. Найти область сходимости степенного ряда
- 23. РЕШЕНИЕ. Интервал сходимости ряда
- 24. Выясним поведение ряда на концах интервала. При
- 25. 1 Члены ряда убывают по абсолютной величине: 2 Предел общего члена равен нулю: Ряд сходится.
- 26. При ряд принимает вид: Это обобщенный
Слайд 214.1. ОБЛАСТЬ СХОДИМОСТИ
СТЕПЕННОГО РЯДА
Рассмотрим ряды, членами которых являются не числа,
Такие ряды называются функциональными.
Будем рассматривать степенные ряды, членами которых являются степенные функции.
Слайд 4При разных значениях х будут получаться разные числовые ряды, которые могут
Совокупность значений х, при которых
степенной ряд (1) сходится, называется
областью сходимости степенного ряда.
Слайд 5Частичная сумма степенного ряда
будет функцией от переменной х .
Следовательно, последовательность
Слайд 7РЕШЕНИЕ.
Данный ряд можно рассматривать как геометрический при
который сходится при
Т.е. областью
Слайд 8ТЕОРЕМА АБЕЛЯ
1
Если степенной ряд сходится при
то он сходится, и при
Слайд 10ДОКАЗАТЕЛЬСТВО:
По условию ряд (1) сходится при
Следовательно выполняется необходимый признак сходимости:
Поэтому последовательность
1
Слайд 11Рассмотрим ряд, состоящий из абсолютных величин ряда (1):
Запишем его в виде:
ограничена,
Слайд 12который можно рассматривать как сходящийся геометрический ряд при
Следовательно по признаку сравнения
Согласно неравенству (2), члены этого ряда меньше членов ряда
Слайд 132
По условию ряд (1) расходится при
Покажем, что он будет расходится для
Предположим от противного, что при
ряд сходится. Тогда, по доказанному выше, он должен сходится и при
Что противоречит условию, следовательно ряд будет расходится при
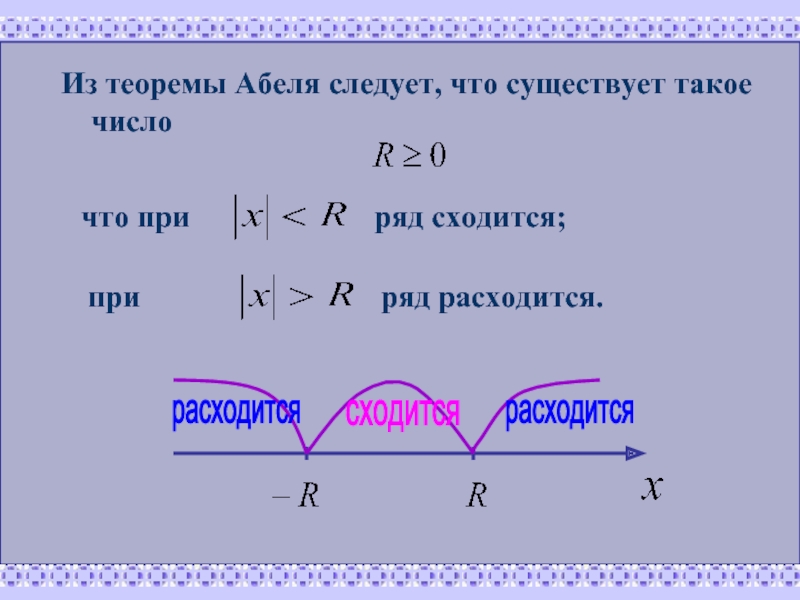
Слайд 14Из теоремы Абеля следует, что существует такое число
что при
ряд сходится;
при
ряд
расходится
расходится
сходится
Слайд 15Если степенной ряд сходится не только
при х=0, то существует такое
положительное число R (возможно и
бесконечное), что ряд абсолютно сходится
в интервале (-R,R) и расходится
везде вне этого интервала.
ТЕОРЕМА.
Слайд 16ДОКАЗАТЕЛЬСТВО:
Пусть Х – множество точек х, в которых ряд (1) сходится.
Пусть х1 – точка, где ряд расходится.
Тогда по теореме Абеля для любого х выполняется условие:
Значит у этого множества существует верхняя грань R >0, поскольку ряд сходится не только при х=0.
Слайд 17Если не существует такой точки х1, где ряд расходится, то
и
Пусть х – любе число, удовлетворяющее условию
или
Тогда по теореме Абеля при этих значениях х имеет место абсолютная сходимость ряда (1).
Слайд 18Пусть теперь х – любе число, удовлетворяющее условию
если
Такие значения х находятся
Слайд 19Число R называется радиусом сходимости,
а интервал (-R,R) – интервалом
сходимости степенного ряда.
На
ряд может как сходиться, так и расходиться.
Найдем выражение для радиуса сходимости степенного ряда через его коэффициенты.
Рассмотрим ряд, состоящий из абсолютных величин членов ряда (1):
Слайд 20Коэффициенты этого ряда, по крайней мере, начиная с некоторого номера, отличны
По признаку Даламбера ряд будет сходится, если
Если этот предел существует, то он и является радиусом сходимости ряда.
Слайд 24Выясним поведение ряда на концах интервала.
При
ряд принимает вид:
Это знакочередующийся ряд.
Слайд 26При
ряд принимает вид:
Это обобщенный гармонический ряд при
у которого все члены
Область сходимости ряда