- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Обходы. Эйлеров и гаильтонов графы презентация
Содержание
- 1. Обходы. Эйлеров и гаильтонов графы
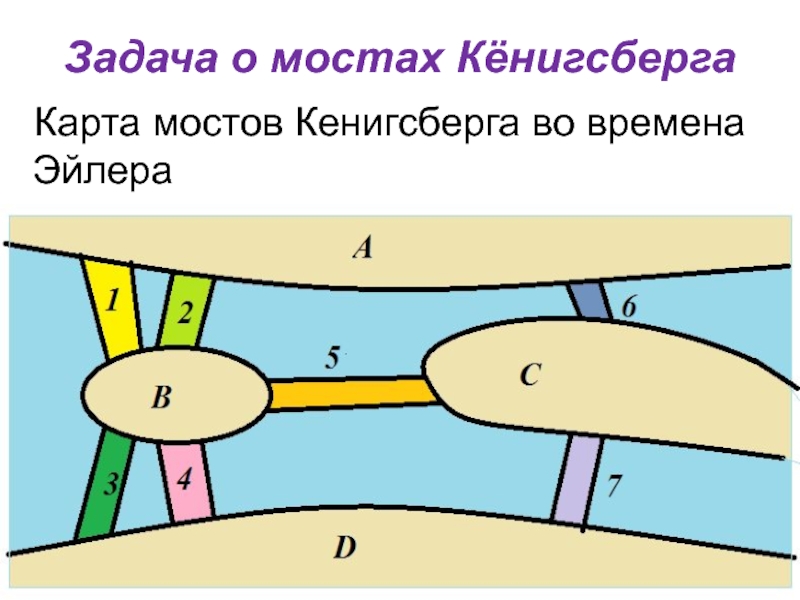
- 2. Задача о мостах Кёнигсберга Карта мостов Кенигсберга во времена Эйлера
- 3. Граф – схема
- 4. Известные головоломки Сабли
- 5. Эйлеров граф Эйлеровым
- 6. Полуэйлеров граф Эйлеровой
- 7. Теорема Эйлера
- 8. Теорема (условие полуэйлеровости
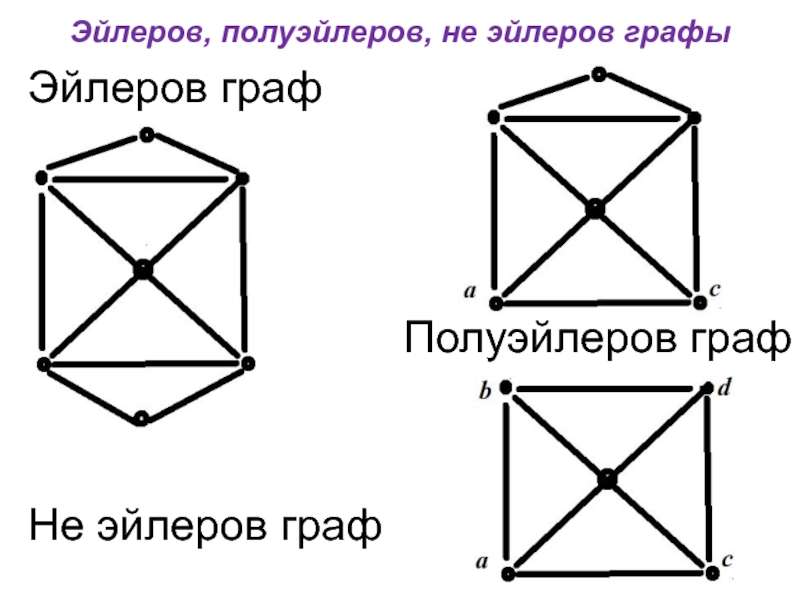
- 9. Эйлеров, полуэйлеров, не
- 10. Алгоритм Флери При
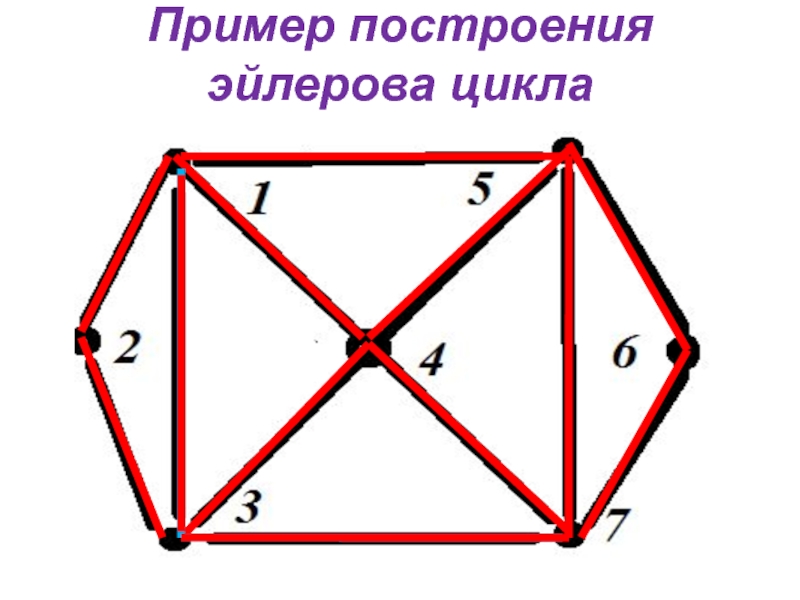
- 11. Пример построения эйлерова цикла
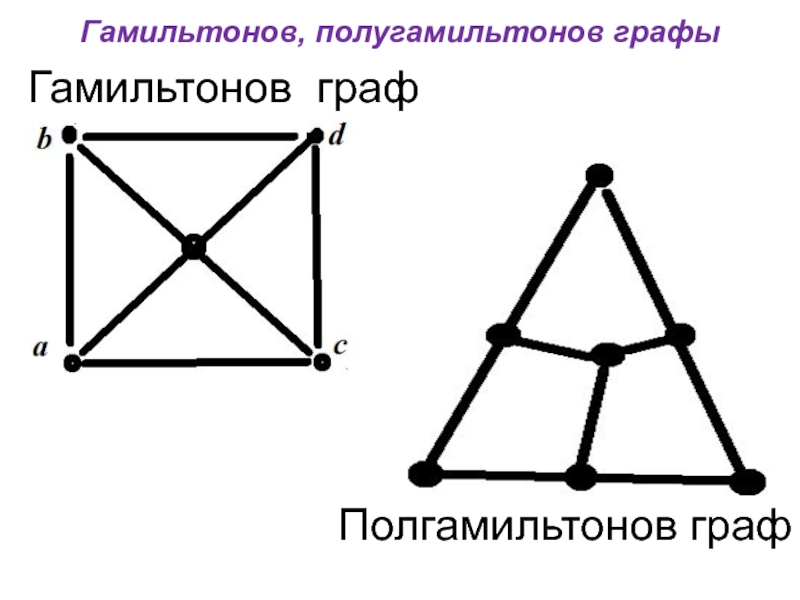
- 12. Гамильтонов граф Гамильтоновым
- 13. Полугамильтонов граф Гамильтоновой
- 14. Гамильтонов, полугамильтонов графы
Слайд 3
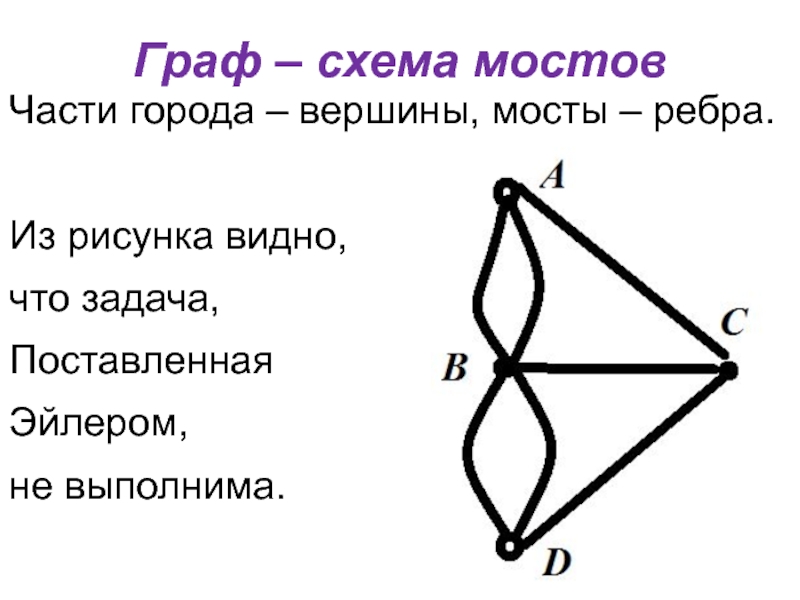
Граф – схема мостов
Части города – вершины, мосты – ребра.
Из рисунка
видно,
что задача,
Поставленная
Эйлером,
не выполнима.
что задача,
Поставленная
Эйлером,
не выполнима.
Слайд 5
Эйлеров граф
Эйлеровым циклом в н-графе называется цикл, обходящий все ребра графа
(ровно по одному разу.
Эйлеров граф – граф, в котором есть эйлеров цикл
Эйлеров граф – граф, в котором есть эйлеров цикл
Слайд 6
Полуэйлеров граф
Эйлеровой цепью в н-графе называется цепь, обходящая все ребра графа
(ровно по одному разу).
Полуэйлеров граф – граф, в котором есть эйлерова цепь
Полуэйлеров граф – граф, в котором есть эйлерова цепь
Слайд 7
Теорема Эйлера
(условие эйлеровости графа)
Для того, чтобы произвольный
н-граф был эйлеровым, необходимо и достаточно, чтобы
он был связен и
локальные степени всех его вершин были четными.
он был связен и
локальные степени всех его вершин были четными.
Слайд 8
Теорема (условие полуэйлеровости графа)
Для того, чтобы произвольный н-граф был полуэйлеровым, необходимо
и достаточно, чтобы: 1) он был связен и
2) локальные степени всех его вершин, кроме двух, были четными. Вершины с нечетными степенями являются началом и концом эйлеровой цепи
2) локальные степени всех его вершин, кроме двух, были четными. Вершины с нечетными степенями являются началом и концом эйлеровой цепи
Слайд 10
Алгоритм Флери
При построении эйлерова цикла начинаем с произвольной вершины и двигаемся
в произвольном направлении выполняя два условия:
стираем пройденные ребра и изолированные вершины, которые при этом появляются;
идем по мосту, только если нет другой возможности.
стираем пройденные ребра и изолированные вершины, которые при этом появляются;
идем по мосту, только если нет другой возможности.
Слайд 12
Гамильтонов граф
Гамильтоновым циклом в н-графе называется простой цикл, обходящий все вершины
графа (ровно по одному разу).
Гамильтонов граф – граф, в котором есть гамильтонов цепь.
Гамильтонов граф – граф, в котором есть гамильтонов цепь.
Слайд 13
Полугамильтонов граф
Гамильтоновой цепью в н-графе называется простая цепь, обходящий все вершины
графа (ровно по одному разу).
Полугамильтонов граф – граф, в котором есть гамильтонова цикл.
Полугамильтонов граф – граф, в котором есть гамильтонова цикл.