- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Статистика, часть 2 презентация
Содержание
- 1. Статистика, часть 2
- 2. Условные обозначения 2*2=4 Быть или не быть?
- 3. АНАЛИЗ ЭМПИРИЧЕСКИХ РАСПРЕДЕЛЕНИЙ
- 4. Анализ эмпирических распределений = детальное исследование
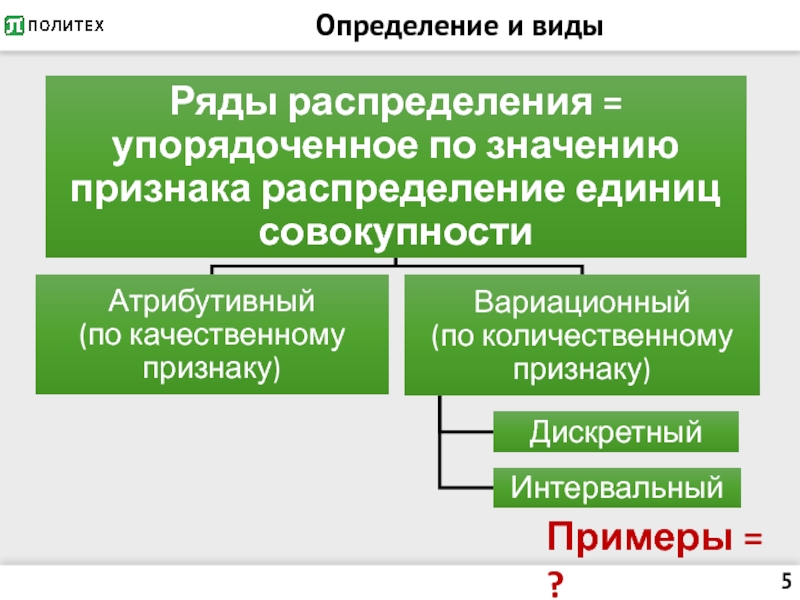
- 5. Определение и виды Примеры = ?
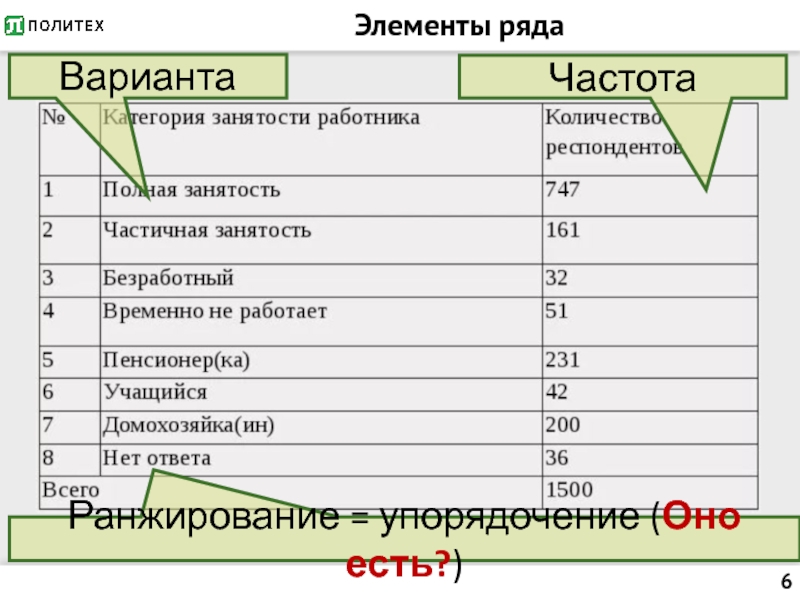
- 6. Элементы ряда Варианта Частота Ранжирование = упорядочение (Оно есть?)
- 8. Ракеты КНДР
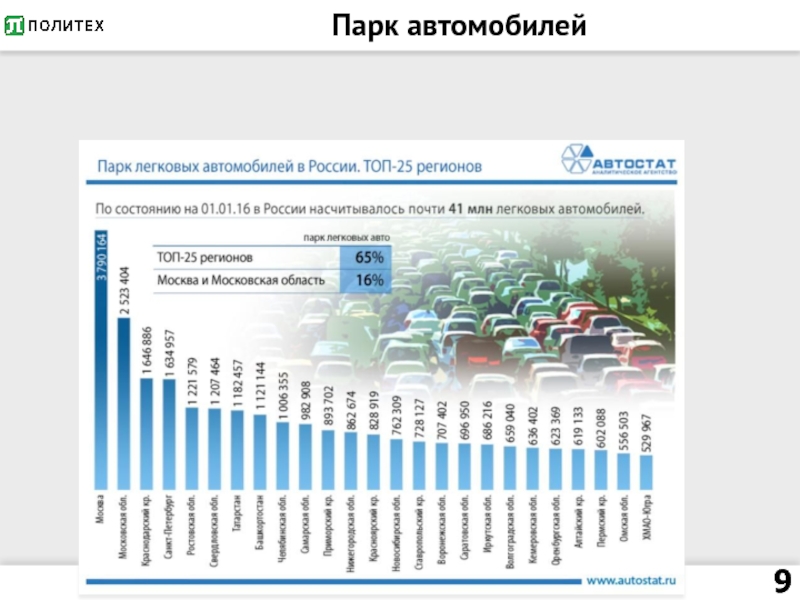
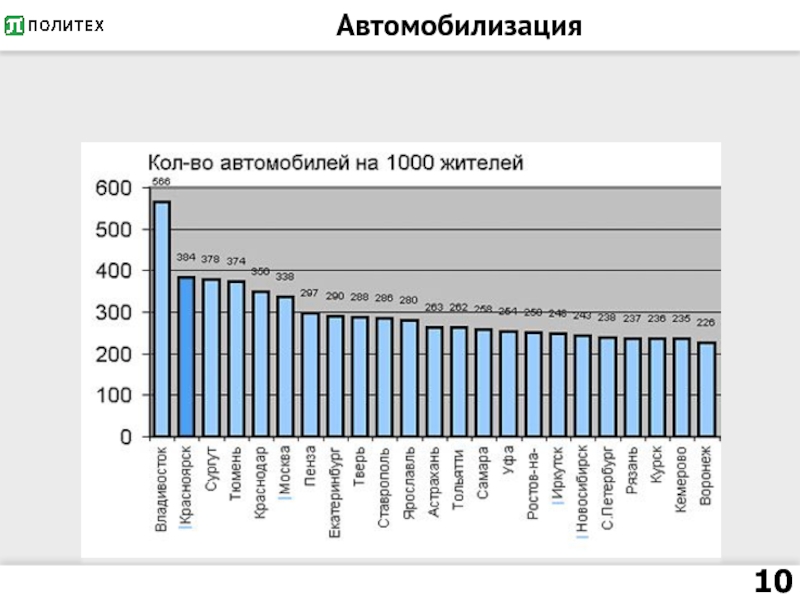
- 9. Парк автомобилей
- 10. Автомобилизация
- 11. Показатели центра распределения
- 12. Показатели центра распределения Арифметическое среднее значение
- 13. Мода интервального ряда Мо – мода, x0 – значение
- 14. Медиана интервального ряда Как понимать границы? Интервал,
- 15. Медиана интервального ряда
- 16. Медиана интервального ряда где xMe — нижняя граница
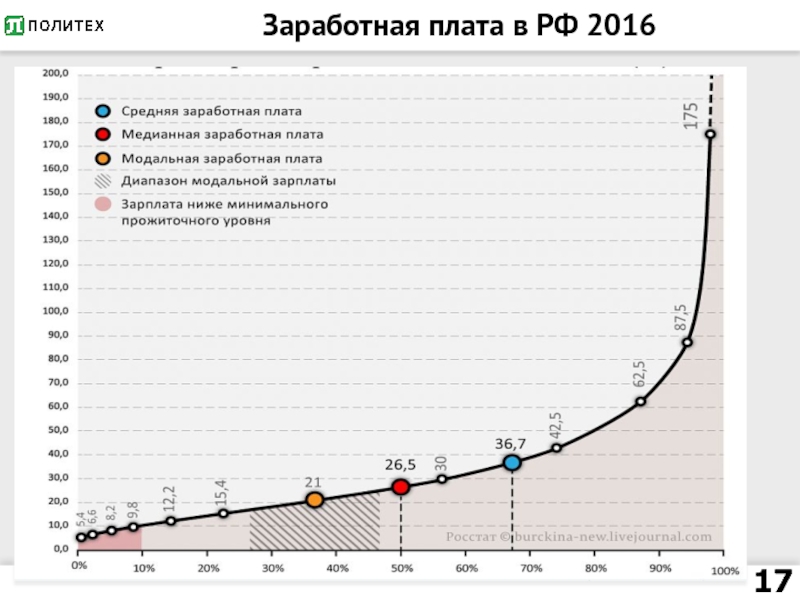
- 17. Заработная плата в РФ 2016
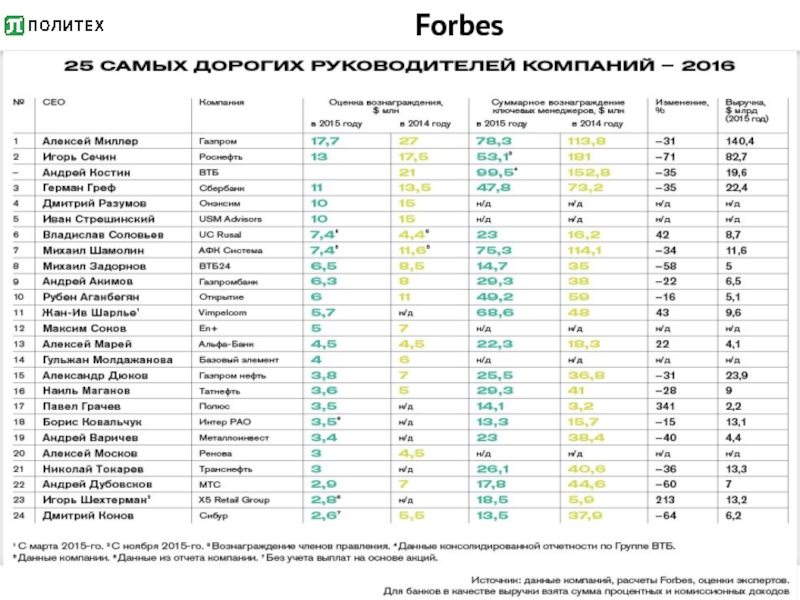
- 18. Forbes
- 19. Показатели структуры распределения
- 20. Показатели структуры распределения Медиана Кварт’или
- 21. Перцентили Это характеристики данных, которые выражают ранги
- 22. Выбросы
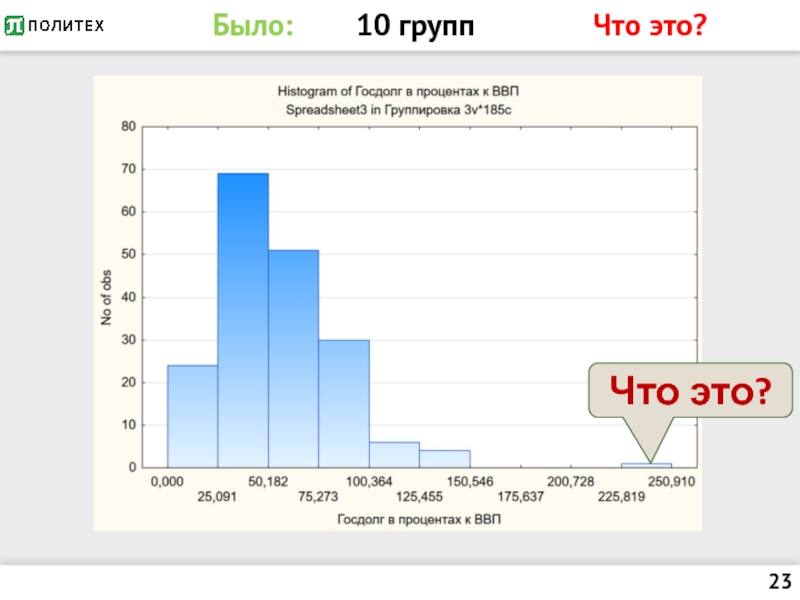
- 23. Было: 10 групп
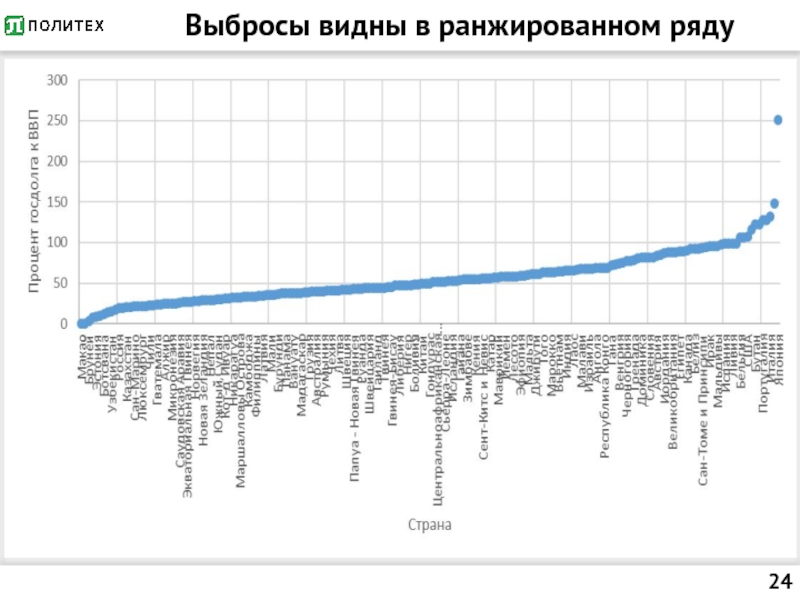
- 24. Выбросы видны в ранжированном ряду
- 25. Выбросы Это единицы совокупности, значения признака которых
- 26. Метод Тьюки Границы ящика – 1-й (снизу)
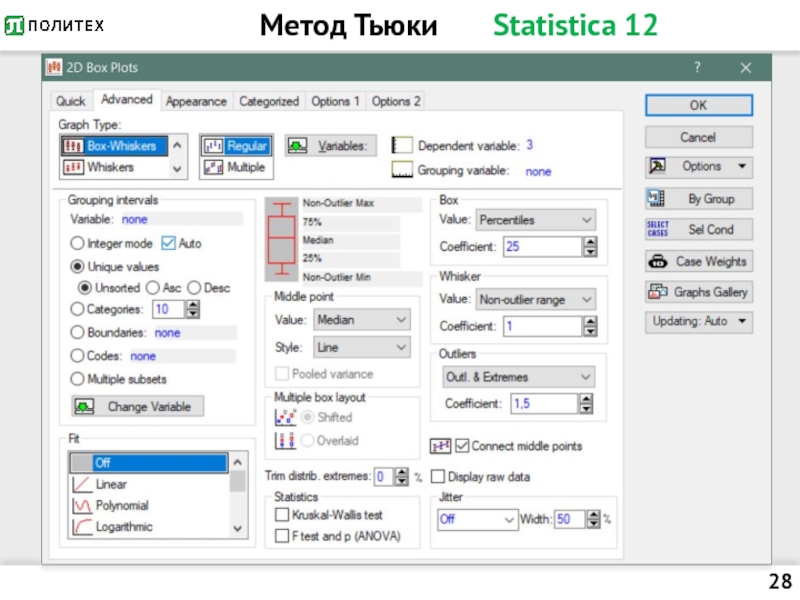
- 28. Метод Тьюки Statistica 12
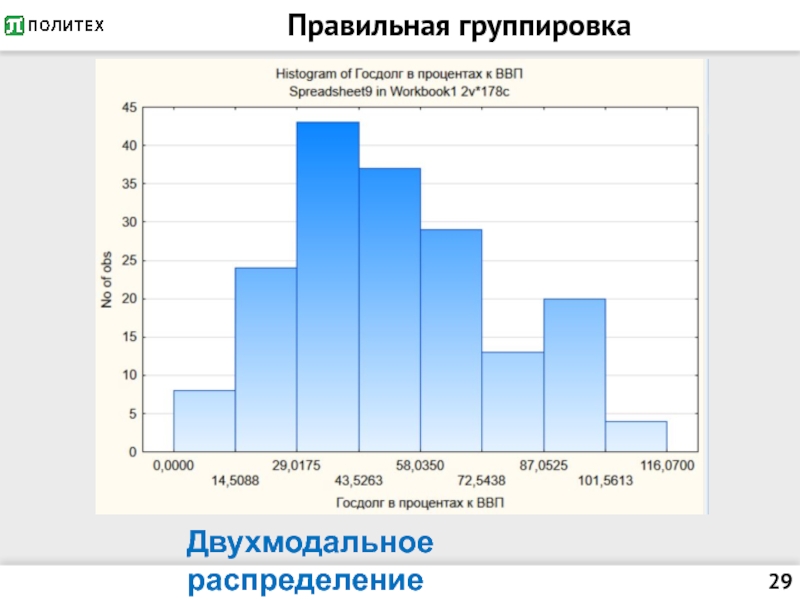
- 29. Правильная группировка Двухмодальное распределение
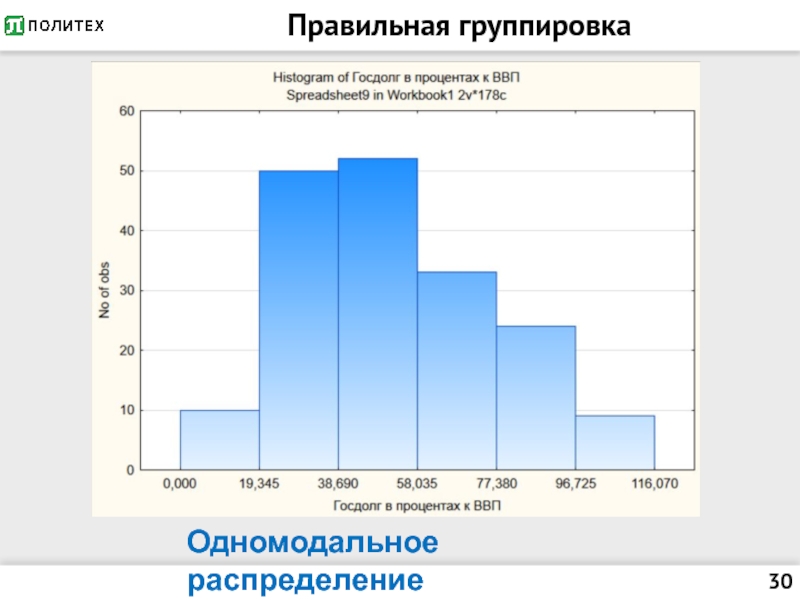
- 30. Правильная группировка Одномодальное распределение
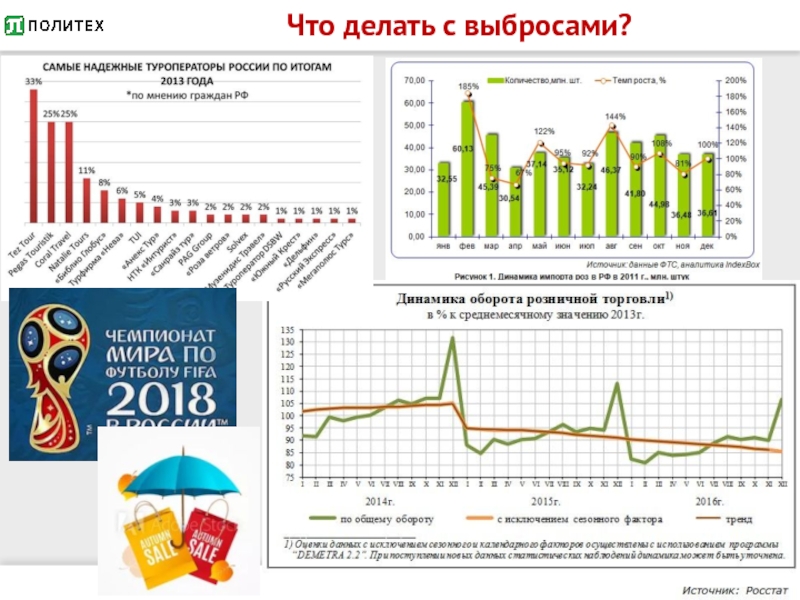
- 31. Что делать с выбросами?
- 32. Показатели вариации
- 33. Что это и зачем Вариация = различия
- 34. Показатели вариации Показатели вариации Абсолютные Относительные Размах
- 35. Абсолютные показатели вариации
- 36. Размах вариации R = Xmax
- 37. Среднее линейное отклонение
- 38. Дисперсия Физического смысла нет, но часто используется
- 39. Среднее квадратическое отклонение = стандартное = типовое отклонение
- 40. Правило Бьеномэ-Чебышева Независимо от формы распределения, процент
- 41. Относительные показатели вариации
- 42. Коэффициент осцилляции R
- 43. Относительное линейное отклонение
- 44. Коэффициент вариации
- 45. Пример коэффициента вариации Средняя заработная плата 50
- 46. Характеристики формы распределения
- 47. Коэффициент асимметрии Пирсона Mo – мода, – среднее квадратическое (стандартное) отклонение. Асимметрия
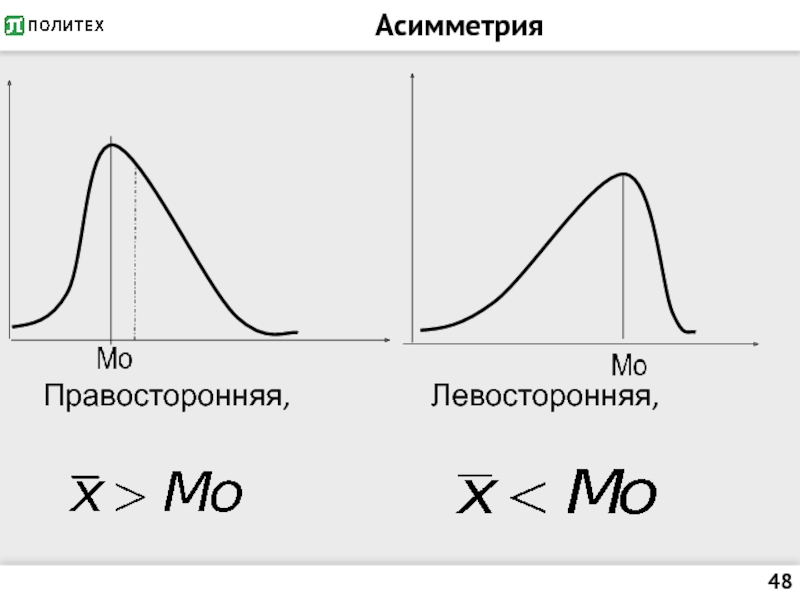
- 48. Асимметрия Правосторонняя, Левосторонняя,
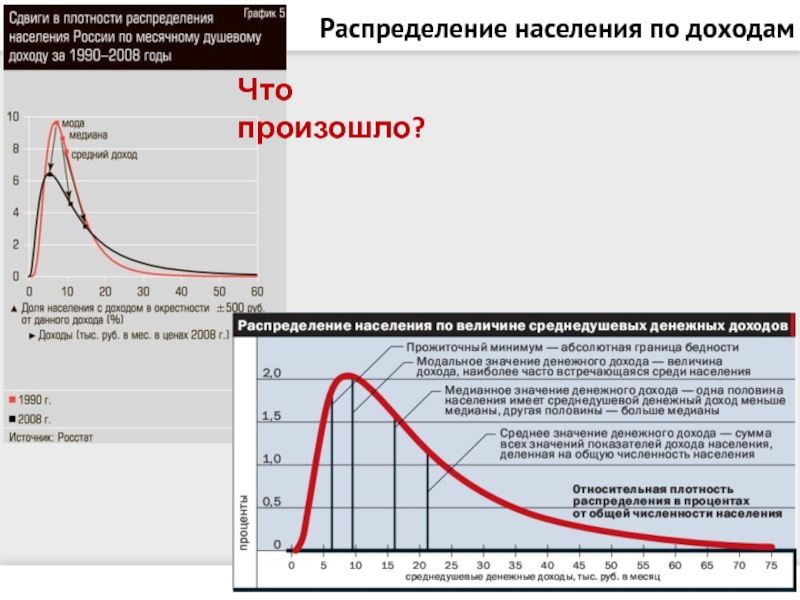
- 49. Распределение населения по доходам Что произошло?
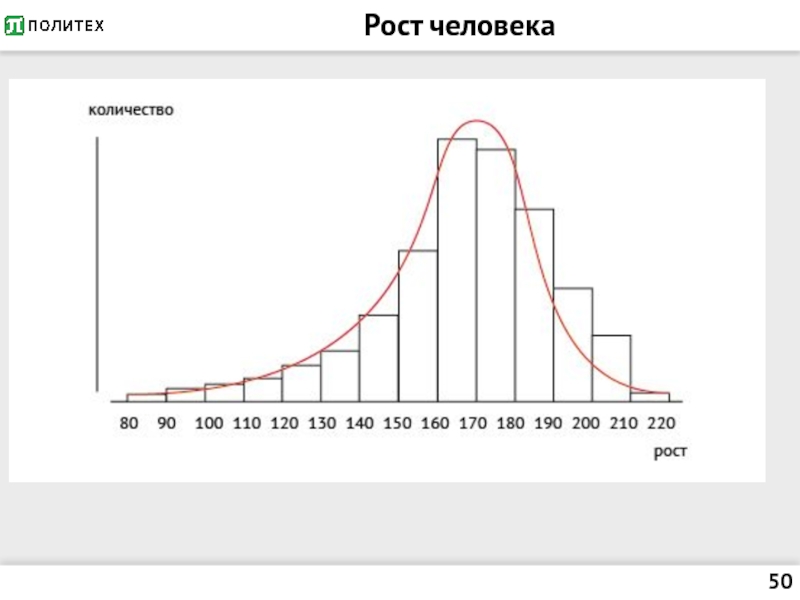
- 50. Рост человека
- 51. Рост человека
- 52. Законы распределения вероятностей Нормальное Логарифмически нормальное Пуассона Биноминальное … … … …
- 53. Нормальное распределение Плотность распределения
- 54. О лазерном луче
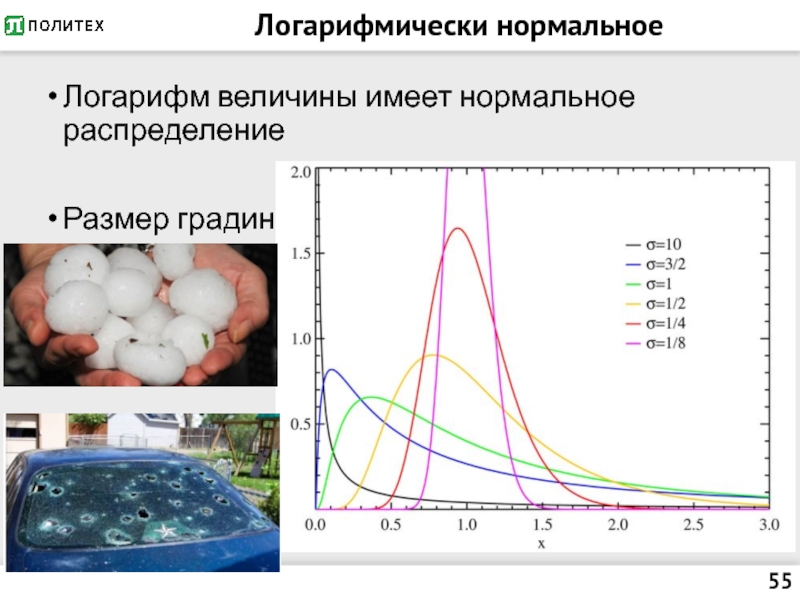
- 55. Логарифмически нормальное Логарифм величины имеет нормальное распределение Размер градин
- 56. Распределение Пуассона Вероятностное распределение дискретного типа. Моделирует
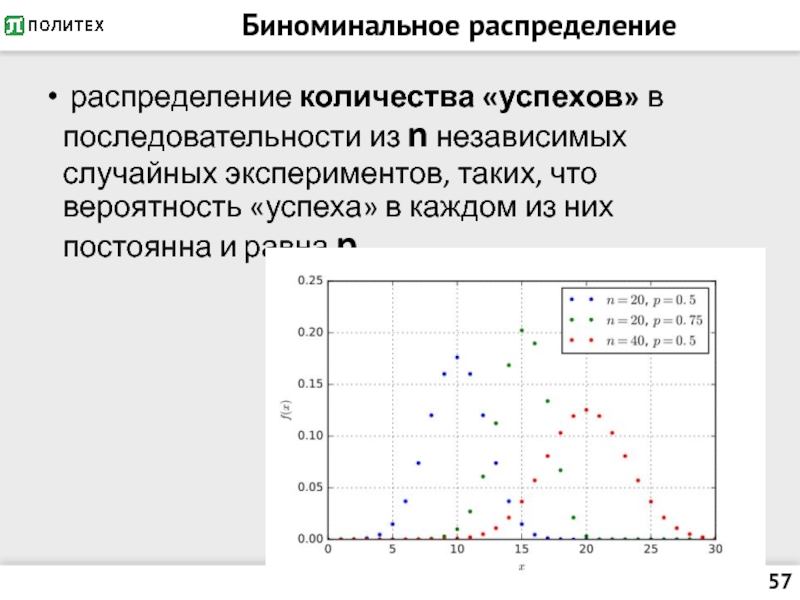
- 57. Биноминальное распределение распределение количества «успехов» в
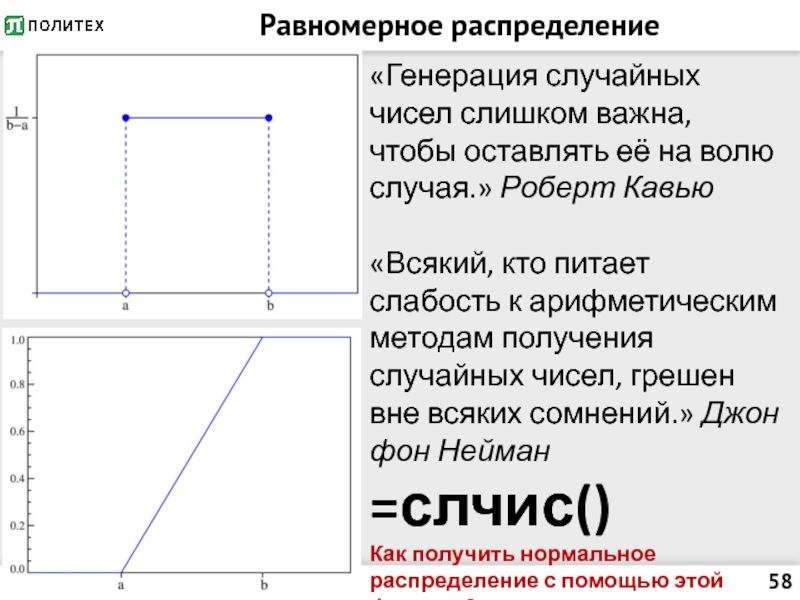
- 58. Равномерное распределение «Генерация случайных чисел
- 59. Законы распределения вероятностей Реальность
- 60. Конец части 2
Слайд 2Условные обозначения
2*2=4
Быть или не быть?
Это самое важное, надо знать на 100%!!!
Это
надо решить и записать!!!
Слайд 4
Анализ эмпирических распределений = детальное исследование одномерных массивов данных.
Комплексный анализ
рядов распределения включает:
1. Табличное и графическое представление ряда распределения.
2. Расчет и анализ показателей центра и структуры распределения.
3. Расчет и анализ показателей вариации.
4. Характеристику формы распределения.
5. Выравнивание эмпирического распределения и оценку его соответствия тому или иному типу теоретических распределений.
1. Табличное и графическое представление ряда распределения.
2. Расчет и анализ показателей центра и структуры распределения.
3. Расчет и анализ показателей вариации.
4. Характеристику формы распределения.
5. Выравнивание эмпирического распределения и оценку его соответствия тому или иному типу теоретических распределений.
Слайд 12Показатели центра распределения
Арифметическое среднее значение
Мода
Для атрибутивного ряда (категория занятости) = ?
Для
дискретного ряда (размер обуви) = ?
Для интервального ряда = ?
Медиана
Для атрибутивного ряда (уровень образования) = ?
Для дискретного ряда (размер обуви)= ?
Для интервального ряда = ?
Для интервального ряда = ?
Медиана
Для атрибутивного ряда (уровень образования) = ?
Для дискретного ряда (размер обуви)= ?
Для интервального ряда = ?
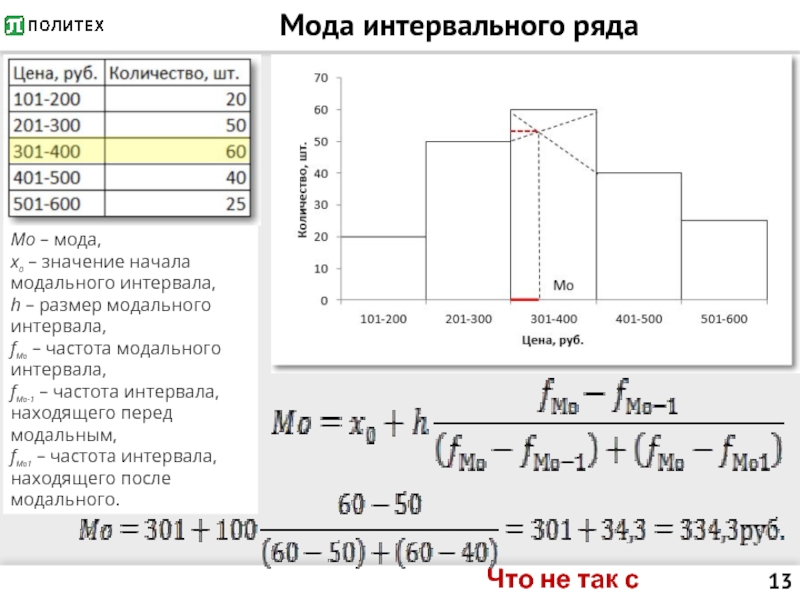
Слайд 13Мода интервального ряда
Мо – мода,
x0 – значение начала модального интервала,
h – размер модального интервала,
fМо –
частота модального интервала,
fМо-1 – частота интервала, находящего перед модальным,
fМо1 – частота интервала, находящего после модального.
fМо-1 – частота интервала, находящего перед модальным,
fМо1 – частота интервала, находящего после модального.
Что не так с границами?
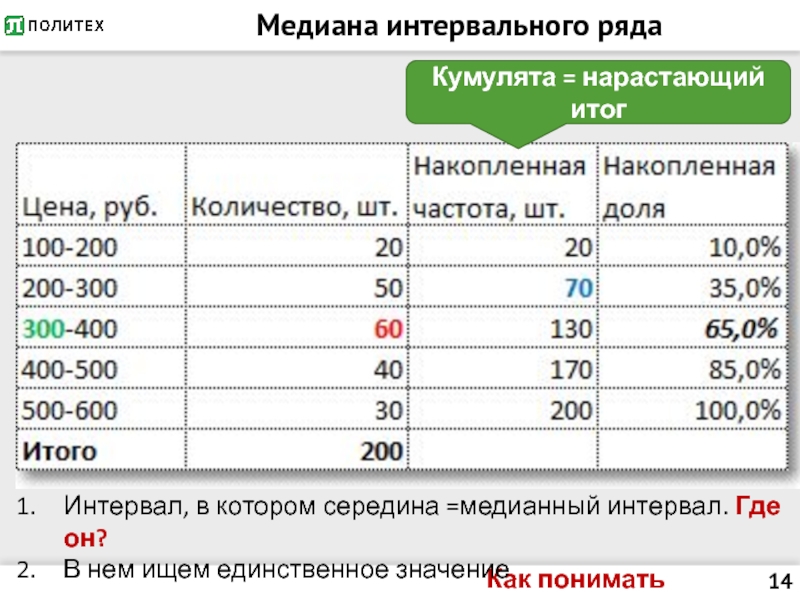
Слайд 14Медиана интервального ряда
Как понимать границы?
Интервал, в котором середина =медианный интервал. Где
он?
В нем ищем единственное значение
В нем ищем единственное значение
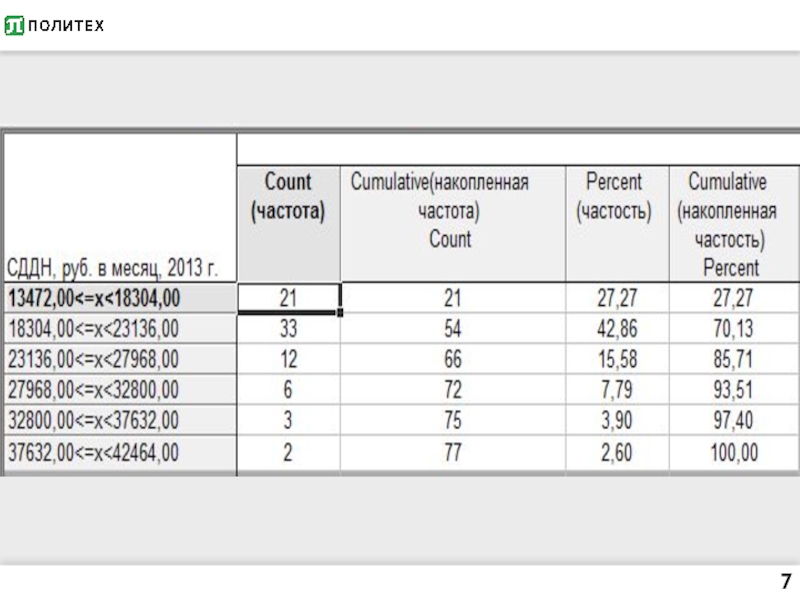
Кумулята = нарастающий итог
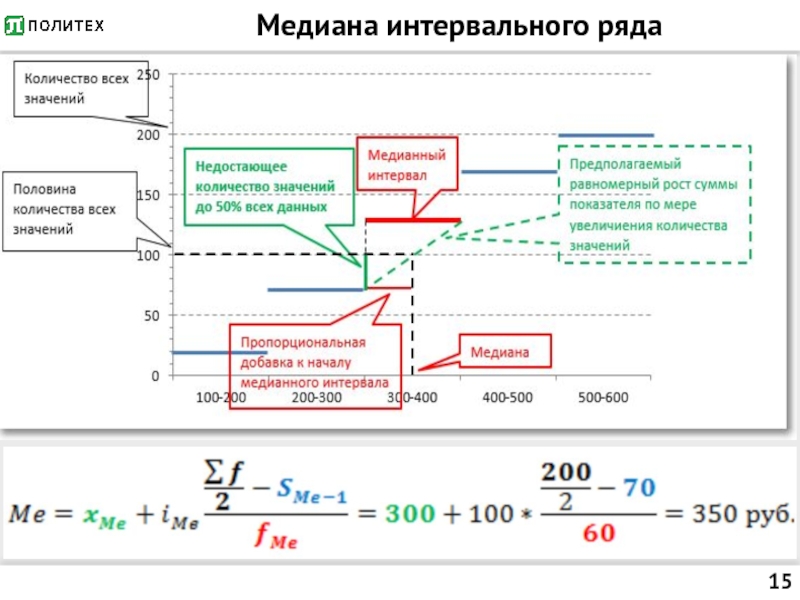
Слайд 16Медиана интервального ряда
где
xMe — нижняя граница медианного интервала;
iMe — ширина медианного интервала;
∑f/2 — количество
всех значений, деленное на 2 (два);
S(Me-1)— суммарное количество наблюдений, которое было накоплено до начала медианного интервала, т.е. накопленная частота предмедианного интервала;
fMe — число наблюдений в медианном интервале.
S(Me-1)— суммарное количество наблюдений, которое было накоплено до начала медианного интервала, т.е. накопленная частота предмедианного интервала;
fMe — число наблюдений в медианном интервале.
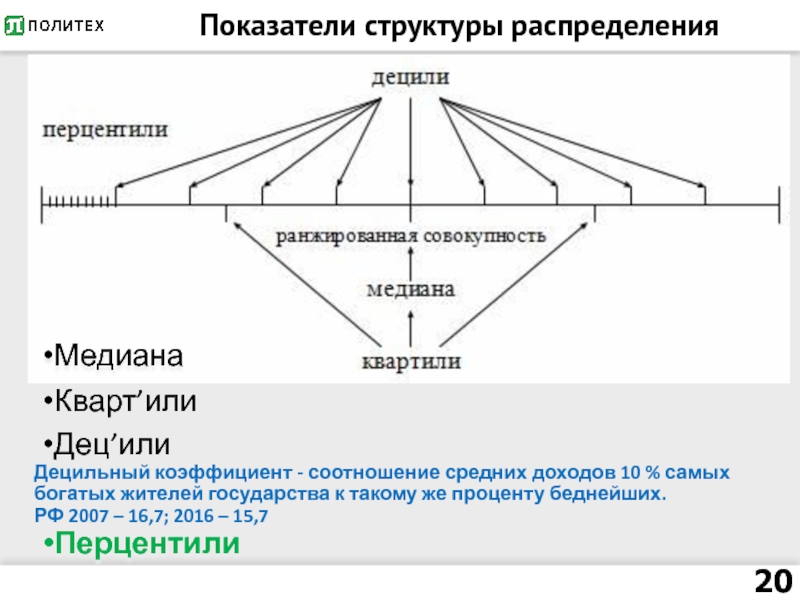
Слайд 20Показатели структуры распределения
Медиана
Кварт’или
Дец’или
Децильный коэффициент - соотношение средних доходов 10 % самых
богатых жителей государства к такому же проценту беднейших.
РФ 2007 – 16,7; 2016 – 15,7
Перцентили
РФ 2007 – 16,7; 2016 – 15,7
Перцентили
Слайд 21Перцентили
Это характеристики данных, которые выражают ранги элементов в виде процентов (от
0 до 100%), а не в числах.
Наименьшему значению признака соответствует нулевой перцентиль, наибольшему – 100-й.
Перцентили – это показатели, разбивающие ранжированный ряд данных на определенное число частей.
Наименьшему значению признака соответствует нулевой перцентиль, наибольшему – 100-й.
Перцентили – это показатели, разбивающие ранжированный ряд данных на определенное число частей.
Слайд 25Выбросы
Это единицы совокупности, значения признака которых резко отличаются в меньшую или
большую сторону от основной массы значений признака.
Данные единицы не подчиняются общей закономерности распределения, поэтому анализируются отдельно.
Данные единицы не подчиняются общей закономерности распределения, поэтому анализируются отдельно.
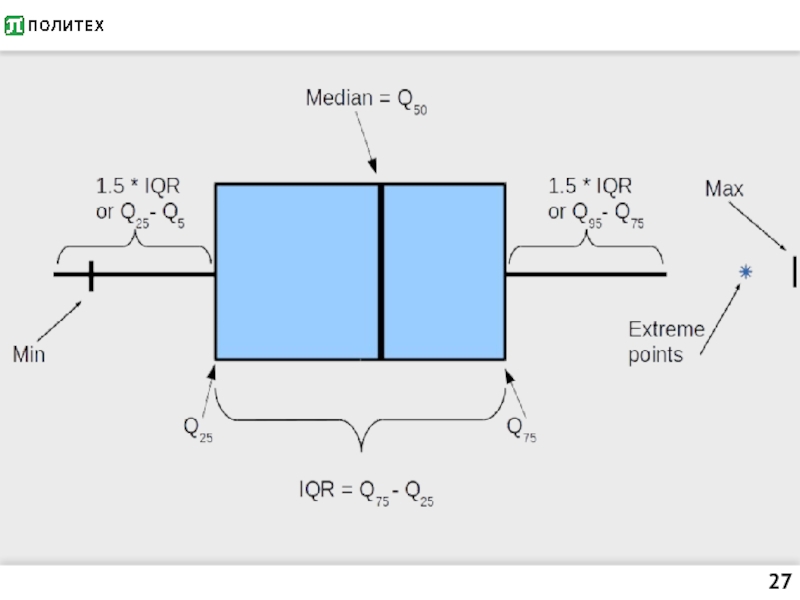
Слайд 26Метод Тьюки
Границы ящика – 1-й (снизу) и 3-й квартили
Ширина ящика =
интерквартиль-ный размах
Ус = полтора интерквартиль-ных размаха от ящика
Почему медиана не посередине?
Почему разные усы???
Ус = полтора интерквартиль-ных размаха от ящика
Почему медиана не посередине?
Почему разные усы???
Слайд 33Что это и зачем
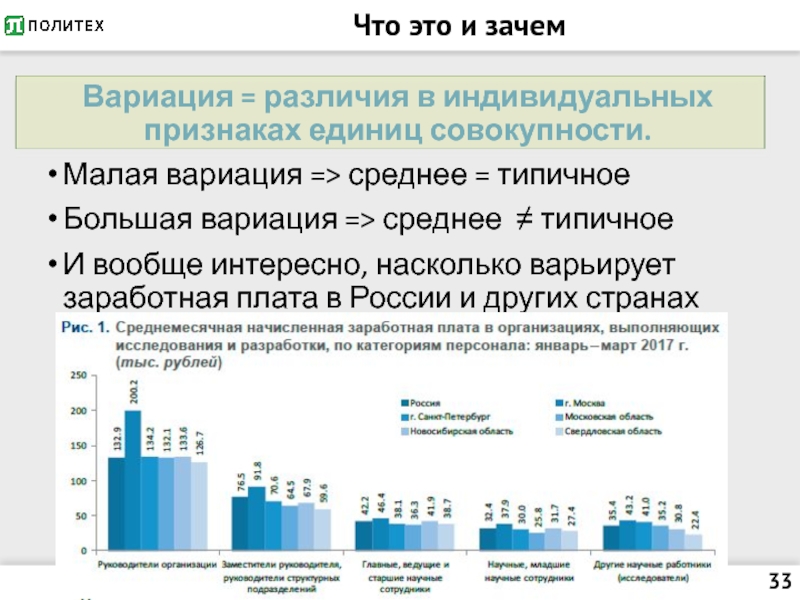
Вариация = различия в индивидуальных признаках единиц совокупности.
Малая
вариация => среднее = типичное
Большая вариация => среднее ≠ типичное
И вообще интересно, насколько варьирует заработная плата в России и других странах мира
Большая вариация => среднее ≠ типичное
И вообще интересно, насколько варьирует заработная плата в России и других странах мира
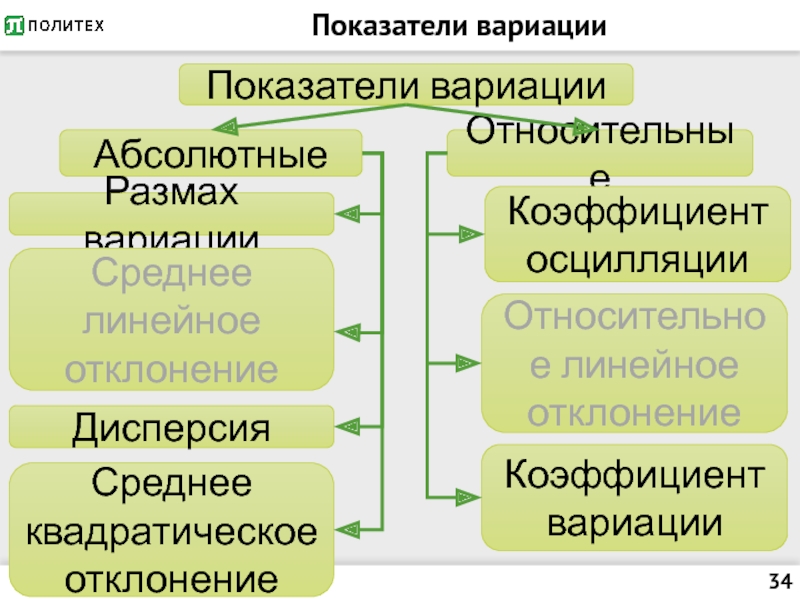
Слайд 34Показатели вариации
Показатели вариации
Абсолютные
Относительные
Размах вариации
Среднее линейное отклонение
Дисперсия
Среднее квадратическое отклонение
Коэффициент осцилляции
Относительное линейное отклонение
Коэффициент
вариации
Слайд 36Размах вариации
R = Xmax - Xmin
Xmax, Xmin – максимальное и
минимальное значения признака в изучаемой совокупности
Зависит от двух измерений, поэтому неустойчив Это как так?
Пример: размах зарплаты по СПб
Зависит от двух измерений, поэтому неустойчив Это как так?
Пример: размах зарплаты по СПб
Слайд 37Среднее линейное отклонение
- среднее значение признака в совокупности;
-
индивидуальные значения признака;
- вес или частота (частость).
Формула попроще, без взвешивания = ?
- вес или частота (частость).
Формула попроще, без взвешивания = ?
Слайд 40Правило Бьеномэ-Чебышева
Независимо от формы распределения, процент наблюдений, лежащих на расстоянии, не
превышающем k стандартных отклонений от среднего значения, не меньше:
для k=2:
для k=2:
Слайд 43Относительное линейное отклонение
- среднее линейное отклонение,
- среднее значение признака
в совокупности.
Слайд 44Коэффициент вариации
- среднее значение признака в совокупности;
-
среднее квадратическое (стандартное) отклонение.
Слайд 45Пример коэффициента вариации
Средняя заработная плата 50 тыс, СКО = 5 тыс.
Прогноз
ВВП РФ на следующий год (мой личный) 75 трлн. руб = 75 000 000 млн. руб. СКО = 5 млн.
Какая оценка более точна?
Вариация заработной платы = 5/50*100 = 10%
Вариация ВВП = 5/75 000 000*100 = 0,000007%
Какая оценка более точна?
Вариация заработной платы = 5/50*100 = 10%
Вариация ВВП = 5/75 000 000*100 = 0,000007%
Слайд 47Коэффициент асимметрии Пирсона
Mo – мода,
– среднее квадратическое (стандартное) отклонение.
Асимметрия
Слайд 52Законы распределения вероятностей
Нормальное
Логарифмически нормальное
Пуассона
Биноминальное
… … … …
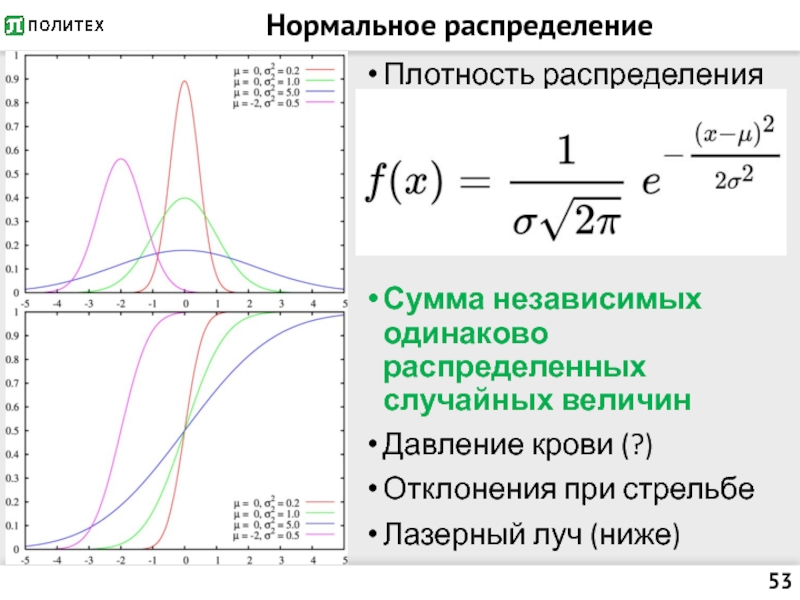
Слайд 53Нормальное распределение
Плотность распределения
Сумма независимых одинаково распределенных случайных величин
Давление крови (?)
Отклонения при
стрельбе
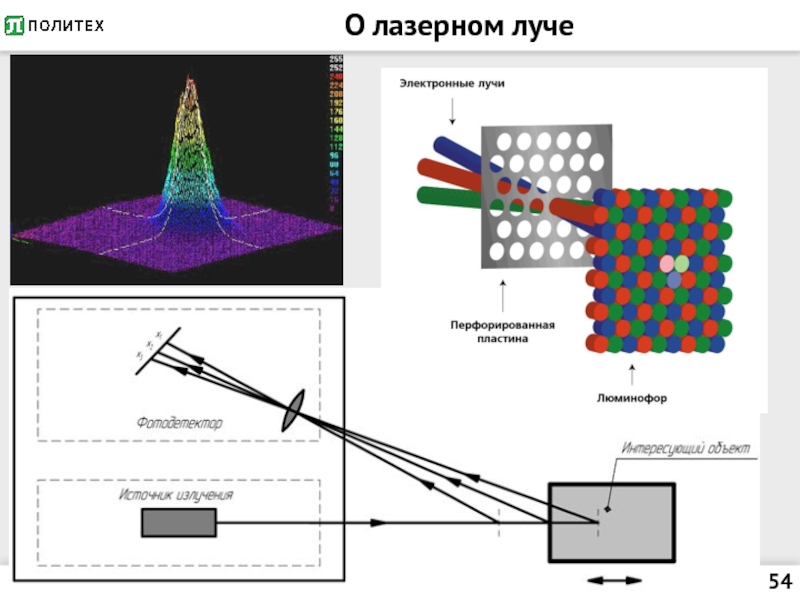
Лазерный луч (ниже)
Лазерный луч (ниже)
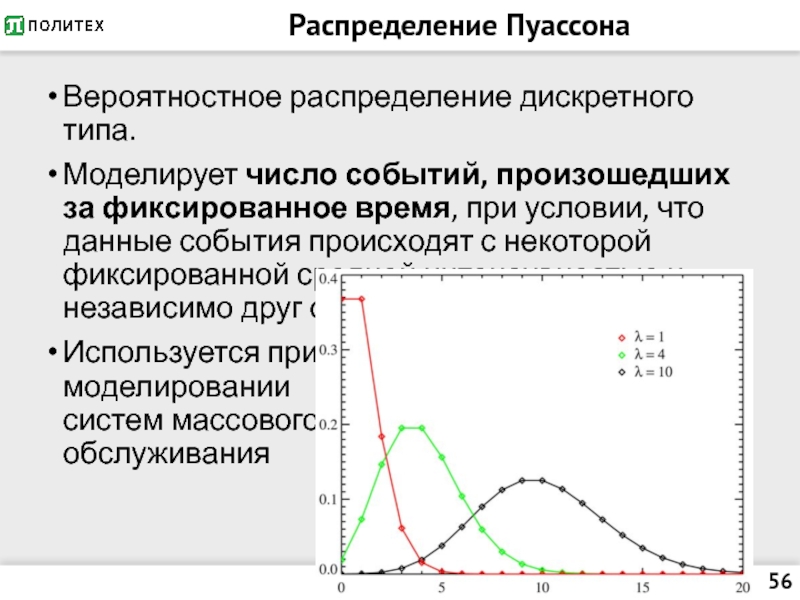
Слайд 56Распределение Пуассона
Вероятностное распределение дискретного типа.
Моделирует число событий, произошедших за фиксированное время,
при условии, что данные события происходят с некоторой фиксированной средней интенсивностью и независимо друг от друга.
Используется при моделировании систем массового обслуживания
Используется при моделировании систем массового обслуживания
Слайд 57Биноминальное распределение
распределение количества «успехов» в последовательности из n независимых случайных
экспериментов, таких, что вероятность «успеха» в каждом из них постоянна и равна p.
Слайд 58Равномерное распределение
«Генерация случайных чисел слишком важна, чтобы оставлять её на
волю случая.» Роберт Кавью
«Всякий, кто питает слабость к арифметическим методам получения случайных чисел, грешен вне всяких сомнений.» Джон фон Нейман
=слчис()
Как получить нормальное распределение с помощью этой функции?
«Всякий, кто питает слабость к арифметическим методам получения случайных чисел, грешен вне всяких сомнений.» Джон фон Нейман
=слчис()
Как получить нормальное распределение с помощью этой функции?
Слайд 59Законы распределения вероятностей
Реальность всегда не идеальна
Требуется проверить близость реальных данных теоретическому
распределению
Эта область = проверка гипотез, будет ниже.
Эта область = проверка гипотез, будет ниже.